Relationship of Abrupt Vegetation Change to Climate Change and Ecological Engineering with Multi-Timescale Analysis in the Karst Region, Southwest China
Abstract
:1. Introduction
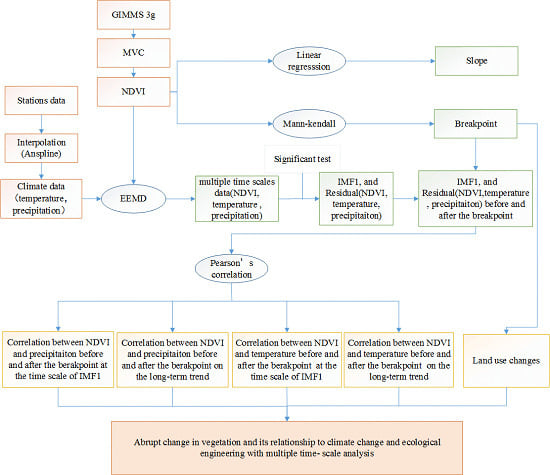
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Mann-Kendall Abrupt Change Test
2.4. Linear Regression Analysis
2.5. Ensemble Empirical Mode Decomposition (EEMD)
2.6. Correlation Analysis
3. Results
3.1. Temporal and Spatial Changes in Vegetation and its Abrupt Change
3.2. Possible Relationships of the Abrupt Change in the NDVI with Climate Change During the Entire Time Period
3.3. Possible Relationships of the Abrupt Change in the NDVI with Climate Changes Based on Multiple Timescales Analysis
3.4. Possible Impacts of the Grain to Green Project (GGP) on the Abrupt Change in Vegetation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peng, J.; Li, Y.; Tian, L.; Liu, Y.; Wang, Y. Vegetation Dynamics and Associated Driving Forces in Eastern China during 1999–2008. Remote Sens. 2015, 7, 13641–13663. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Yang, Y.; Zhou, W.; Gang, C.; Zhang, Y.; Li, J.; An, R.; Wang, K.; Odeh, I. Quantitative assess the driving forces on the grassland degradation in the Qinghai–Tibet Plateau, in China. Ecol. Inform. 2016, 33, 32–44. [Google Scholar] [CrossRef]
- Pan, N.; Feng, X.; Fu, B.; Wang, S.; Ji, F.; Pan, S. Increasing global vegetation browning hidden in overall vegetation greening: Insights from time-varying trends. Remote Sens. Environ. 2018, 214, 59–72. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Liu, L.; Wu, J.; Wang, Z.; Li, S.; Zhang, H.; Zu, J.; Ding, M.; Paudel, B. Comparison of the Vegetation Effect on ET Partitioning Based on Eddy Covariance Method at Five Different Sites of Northern China. Remote Sens. 2018, 10, 1755. [Google Scholar] [Green Version]
- Lü, Y.; Zhang, L.; Feng, X.; Zeng, Y.; Fu, B.; Yao, X.; Li, J.; Wu, B. Recent ecological transitions in China: Greening, browning, and influential factors. Sci. Rep. 2015, 5, 8732. [Google Scholar] [CrossRef] [PubMed]
- Jong, R.D.; Verbesselt, J.; Schaepman, M.E.; Bruin, S.D. Trend changes in global greening and browning: Contribution of short-term trends to longer-term change. Glob. Chang. Biol. 2012, 18, 642–655. [Google Scholar] [CrossRef]
- Chen, B.; Guang, X.; Coops, N.; Ciais, P.; Innes, J.; Wang, G.; Myneni, R. Changes in vegetation photosynthetic activity trends across the Asia-Pacific region over the last three decades. Remote Sens. Environ. 2014, 144, 28–41. [Google Scholar] [CrossRef]
- Phillips, P.C.; Moon, H.R. Linear Regression Limit Theory for Nonstationary Panel Data. Econometrica 1999, 67, 1057–1111. [Google Scholar] [CrossRef] [Green Version]
- Abera, T.A.; Heiskanen, J.; Pellikka, P.; Maeda, E.E. Rainfall–vegetation interaction regulates temperature anomalies during extreme dry events in the Horn of Africa. Glob. Planet. Chang. 2018, 167, 35–45. [Google Scholar] [CrossRef]
- Jing, W.; Wang, K.; Zhang, M.; Zhang, C. Impacts of climate change and human activities on vegetation cover in hilly southern China. Ecol. Eng. 2015, 81, 451–461. [Google Scholar]
- Yi, S.; Long, J.; Wang, H. Vegetation Changes along the Qinghai-Tibet Plateau Engineering Corridor Since 2000 Induced by Climate Change and Human Activities. Remote Sens. 2018, 10, 95. [Google Scholar] [Green Version]
- Wen, Z.; Wu, S.; Chen, J.; Lu, M. NDVI indicated long-term interannual changes in vegetation activities and their responses to climatic and anthropogenic factors in the Three Gorges Reservoir Region, China. Sci. Total Environ. 2017, 574, 947–959. [Google Scholar] [CrossRef] [PubMed]
- Lloret, F.; Escudero, A.; Iriondo, J.M.; Martínez-Vilalta, J.; Valladares, F. Extreme climatic events and vegetation: The role of stabilizing processes. Glob. Chang. Biol. 2012, 18, 797–805. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Yan, Q.; Xue, Y.J. Application of piecewise linear regression in the detection of vegetation greenness trends on the Tibetan Plateau. Int. J. Remote Sens. 2014, 35, 1526–1539. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, M.; Lin, Z. Relative importance of climate changes at different time scales on net primary productivity-a case study of the Karst area of northwest Guangxi, China. Environ. Monit. Assess. 2017, 189, 539. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Shu, J.; Yin, J.; Yuan, X.; Jiaerheng, A.; Xiong, S.; He, P.; Liu, W. Analysis on spatio-temporal trends and drivers in vegetation growth during recent decades in Xinjiang, China. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 216–228. [Google Scholar] [CrossRef]
- Li, S.; Verburg, P.H.; Lv, S.; Wu, J.; Li, X. Spatial analysis of the driving factors of grassland degradation under conditions of climate change and intensive use in Inner Mongolia, China. Reg. Environ. Chang. 2011, 12, 461–474. [Google Scholar] [CrossRef]
- Chen, T.; Peng, L.; Liu, S.; Wang, Q. Spatio-temporal pattern of net primary productivity in Hengduan Mountains area, China: Impacts of climate change and human activities. Chin. Geogr. Sci. 2017, 27, 948–962. [Google Scholar] [CrossRef]
- Piao, S.; Nan, H.; Huntingford, C.; Ciais, P.; Friedlingstein, P.; Sitch, S.; Peng, S.; Ahlstrom, A.; Canadell, J.G.; Cong, N.; et al. Evidence for a weakening relationship between interannual temperature variability and northern vegetation activity. Nat. Commun. 2014, 5, 5018. [Google Scholar] [CrossRef] [Green Version]
- Wei, F.; Wang, S.; Fu, B.; Pan, N.; Feng, X.; Zhao, W.; Wang, C. Vegetation dynamic trends and the main drivers detected using the ensemble empirical mode decomposition method in East Africa. Land. Degrad. Dev. 2018, 29, 2542–2553. [Google Scholar] [CrossRef]
- Liu, Z.; Li, C.; Zhou, P.; Chen, X. A probabilistic assessment of the likelihood of vegetation drought under varying climate conditions across China. Sci. Rep. 2016, 6, 35105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guan, B.T. Ensemble empirical mode decomposition for analyzing phenological responses to warming. Agric. For. Meteorol. 2014, 194, 1–7. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, M.; Lin, Z.; Xu, X. Spatial heterogeneity of the relationship between vegetation dynamics and climate change and their driving forces at multiple time scales in Southwest China. Agric. For. Meteorol. 2018, 256–257, 10–21. [Google Scholar] [CrossRef]
- Hawinkel, P.; Swinnen, E.; Lhermitte, S.; Verbist, B.; Van Orshoven, J.; Muys, B. A time series processing tool to extract climate-driven interannual vegetation dynamics using Ensemble Empirical Mode Decomposition (EEMD). Remote Sens. Environ. 2015, 169, 375–389. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.; Tang, Q.; Wang, L.; Liu, X. Risk and contributing factors of ecosystem shifts over naturally vegetated land under climate change in China. Sci. Rep. 2016, 6, 20905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, L.; Jiapaer, G.; Bao, A.; Guo, H.; Ndayisaba, F. Vegetation dynamics and responses to climate change and human activities in Central Asia. Sci. Total Environ. 2017, 599–600, 967–980. [Google Scholar] [CrossRef]
- Hua, W.; Chen, H.; Zhou, L.; Xie, Z.; Qin, M.; Li, X.; Ma, H.; Huang, Q.; Sun, S. Observational Quantification of Climatic and Human Influences on Vegetation Greening in China. Remote Sens. 2017, 9, 425. [Google Scholar] [CrossRef]
- Rui, L.; Xiao, L.; Zhe, L.; Dai, J. Quantifying the relative impacts of climate and human activities on vegetation changes at the regional scale. Ecol. Indic. 2018, 93, 91–99. [Google Scholar]
- Yin, Y.; Ma, D.; Wu, S.; Dai, E.; Zhu, Z.; Myneni, R.B. Nonlinear variations of forest leaf area index over China during 1982–2010 based on EEMD method. Int. J. Biometeorol. 2017, 61, 977–988. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef] [Green Version]
- Wong, C.M.; Daniels, L.D. Novel forest decline triggered by multiple interactions among climate, an introduced pathogen and bark beetles. Glob. Chang. Biol. 2017, 23, 1926–1941. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Piao, S.; Ciais, P.; Li, J.; Friedlingstein, P.; Koven, C.; Chen, A. Spring temperature change and its implication in the change of vegetation growth in North America from 1982 to 2006. Proc. Natl. Acad. Sci. USA 2011, 108, 1240–1245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Piao, S.; Xu, X.; Ciais, P.; MacBean, N.; Myneni, R.B.; Li, L. Has the advancing onset of spring vegetation green-up slowed down or changed abruptly over the last three decades? Glob. Ecol. Biogeogr. 2015, 24, 621–631. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, Z.; Huang, J. Long-Term Trend and Abrupt Change for Major Climate Variables in the Upper Yellow River Basin. J. Meteorol. Res. 2007, 21, 204–214. [Google Scholar]
- Yang, Y.; Tian, F. Abrupt change of runoff and its major driving factors in Haihe River Catchment, China. J. Hydrol. 2009, 374, 373–383. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank correlation methods. Br. J. Psychol. 1990, 25, 86–91. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Panda, D.K.; Kumar, A.; Mohanty, S. Recent trends in sediment load of the tropical (Peninsular) river basins of India. Glob. Planet. Chang. 2011, 75, 108–118. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. The Mann-Kendall Test Modified by Effective Sample Size to Detect Trend in Serially Correlated Hydrological Series. Water. Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Meng, M. Study on the Influence of Abrupt Climate Variation on the Vegetation Based on NDVI. Meteorol. Environ. Res. Lett. 2011, 2, 68–71. [Google Scholar]
- Jiang, H.; Li, C.; Li, H. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis. Mech. Syst. Signal Process. 2013, 36, 225–239. [Google Scholar] [CrossRef]
- Tong, W.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the applications of EMD and EEMD on time–frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Chi, C.T.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Kong, Y.; Meng, Y.; Li, W.; Yue, A.; Yuan, Y. Satellite Image Time Series Decomposition Based on EEMD. Remote Sens. 2015, 7, 15583–15604. [Google Scholar] [CrossRef] [Green Version]
- Han, S.L. Estimation of extreme sea levels along the Bangladesh coast due to storm surge and sea level rise using EEMD and EVA. J. Geophys. Res. Ocean. 2013, 118, 4273–4285. [Google Scholar]
- Wang, D.; Shen, Y.; Li, Y.; Huang, J. Rock Outcrops Redistribute Organic Carbon and Nutrients to Nearby Soil Patches in Three Karst Ecosystems in SW China. PLoS ONE 2016, 11, e0160773. [Google Scholar] [CrossRef]
- Wang, S.J.; Liu, Q.M.; Zhang, D.F. Karst rocky desertification in southwestern China: Geomorphology, landuse, impact and rehabilitation. Land. Degrad. Dev. 2004, 15, 115–121. [Google Scholar] [CrossRef]
- Yang, J.; Wang, W.; Hu, M.; Mao, R. Extreme drought event of 2009/2010 over southwestern China. Meteorol. Atmos. Phys. 2012, 115, 173–184. [Google Scholar] [CrossRef]
- Xiong, H.F.; Wang, S.J.; Rong, L.; Cheng, A.Y.; Li, Y.B. Effects of extreme drought on plant species in Karst area of Guizhou Province, Southwest China. Chin. J. Appl. Ecol. 2011, 22, 1127–1134. [Google Scholar]
- Zhang, T.; Li, J.; Pu, J.; Martin, J.B.; Khadka, M.B.; Wu, F.; Li, L.; Jiang, F.; Huang, S.; Yuan, D. River sequesters atmospheric carbon and limits the CO2 degassing in karst area, southwest China. Sci. Total Environ. 2017, 609, 92. [Google Scholar] [CrossRef] [PubMed]
- Gascon, M.; Cirach, M.; Martínez, D.; Dadvand, P.; Valentín, A.; Plasència, A.; Nieuwenhuijsen, M.J. Normalized difference vegetation index (NDVI) as a marker of surrounding greenness in epidemiological studies: The case of Barcelona city. Urban For. Urban Green. 2016, 19, 88–94. [Google Scholar] [CrossRef]
- Prevot, T.; Smith, N.M.; Palmer, E.; Callantine, T.J.; Lee, P.U.; Mercer, J.; Martin, L.; Brasil, C.; Cabrall, C. An Overview of Current Capabilities and Research Activities in the Airspace Operations Laboratory at NASA Ames Research Center. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Tong, X.; Brandt, M.; Yue, Y.; Horion, S.; Wang, K.; Keersmaecker, W.D.; Feng, T.; Schurgers, G.; Xiao, X.; Luo, Y. Increased vegetation growth and carbon stock in China karst via ecological engineering. Nat. Sustain. 2018, 1, 44–50. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, H.; Liu, Y.; Xu, Y.; Dai, J. Phenological response of different vegetation types to temperature and precipitation variations in northern China during 1982–2012. Int. J. Remote Sens. 2017, 38, 3236–3252. [Google Scholar] [CrossRef]
- Liu, C.; Melack, J.; Tian, Y.; Huang, H.; Jiang, J.; Fu, X.; Zhang, Z. Detecting Land Degradation in Eastern China Grasslands with Time Series Segmentation and Residual Trend analysis (TSS-RESTREND) and GIMMS NDVI3g Data. Remote Sens. 2019, 11, 1014. [Google Scholar] [CrossRef]
- Tong, S.; Zhang, J.; Ha, S.; Lai, Q.; Ma, Q. Dynamics of Fractional Vegetation Coverage and Its Relationship with Climate and Human Activities in Inner Mongolia, China. Remote Sens. 2016, 8, 776. [Google Scholar] [CrossRef]
- Militino, A.; Ugarte, M.; Pérez-Goya, U. Stochastic Spatio-Temporal Models for Analysing NDVI Distribution of GIMMS NDVI3g Images. Remote Sens. 2017, 9, 76. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, X.; Chen, Y.; Wang, P.; Wei, X.; Tao, F. Dynamic variability of the heading-flowering stages of single rice in China based on field observations and NDVI estimations. Int. J. Biometeorol. 2015, 59, 643–655. [Google Scholar] [CrossRef]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Freijedo, F.D.; Monfared, M. Moving Average Filter Based Phase-Locked Loops: Performance Analysis and Design Guidelines. J. IEEE Trans. Power Electron. 2014, 29, 2750–2763. [Google Scholar] [CrossRef]
- Guan, Q.; Yang, L.; Pan, N.; Lin, J.; Xu, C.; Wang, F.; Liu, Z. Greening and Browning of the Hexi Corridor in Northwest China: Spatial Patterns and Responses to Climatic Variability and Anthropogenic Drivers. Remote Sens. 2018, 10, 1270. [Google Scholar] [CrossRef]
- Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E. A Review of the Application of Optical and Radar Remote Sensing Data Fusion to Land Use Mapping and Monitoring. Remote Sens. 2016, 8, 70. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A.J. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2010, 25, 1965–1978. [Google Scholar] [CrossRef]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Clim. 2010, 26, 707–721. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Li, W. Response of runoff to change of atmospheric 0 °C level height in summer in arid region of Northwest China. Sci. China Earth Sci. 2012, 55, 1533–1544. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Liu, H.; Xu, X.; Lin, Z.; Zhang, M.; Ying, M.; Huang, C.; Hao, Y. Climatic and human impacts on quasi-periodic and abrupt changes of sedimentation rate at multiple time scales in Lake Taihu, China. J. Hydrol. 2016, 543, 739–748. [Google Scholar] [CrossRef]
- Verma, R.; Dutta, S. Vegetation Dynamics from Denoised NDVI Using Empirical Mode Decomposition. J. Indian Soc. Remote Sens. 2013, 41, 555–566. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Yue, Y.; Tong, X.; Liao, C.; Zhang, M.; Jiang, Y. Factors impacting on vegetation dynamics and spatial non-stationary relationships in karst regions of southwest China. Acta Ecol. Sin. 2017, 37, 4008–4018. [Google Scholar]
- Wu, Z.; Huang, E. Ensemble Empirical Mode Decomposition: A Noise Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar] [CrossRef]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Pinzon, J.; Tucker, C. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Cai, H.; Yang, X.; Wang, K.; Xiao, L. Is Forest Restoration in the Southwest China Karst Promoted Mainly by Climate Change or Human-Induced Factors? Remote Sens. 2014, 6, 9895–9910. [Google Scholar] [CrossRef] [Green Version]
- Hou, W.; Gao, J.; Wu, S.; Dai, E. Interannual Variations in Growing-Season NDVI and Its Correlation with Climate Variables in the Southwestern Karst Region of China. Remote Sens. 2015, 7, 11105–11124. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Meng, J.J.; Cai, Y.L. Assessing vegetation dynamics impacted by climate change in the southwestern karst region of China with AVHRR NDVI and AVHRR NPP time-series. Environ. Geol. 2008, 54, 1185–1195. [Google Scholar] [CrossRef]
- Jian, T.; Xu, T.; Dong, J.; Yu, X.; Jiang, Y.; Zhang, Y.; Ke, H.; Zhu, J.; Dong, J.; Xu, Y. Elevation-dependent effects of climate change on vegetation greenness in the high mountains of southwest China during 1982–2013. Int. J. Clim. 2017, 59, 780–794. [Google Scholar]
- Qi, X.; Wang, K.; Zhang, C. Effectiveness of ecological restoration projects in a karst region of southwest China assessed using vegetation succession mapping. Ecol. Eng. 2013, 54, 245–253. [Google Scholar] [CrossRef]
- Tong, X.; Wang, K.; Brandt, M.; Yue, Y.; Liao, C.; Fensholt, R. Assessing Future Vegetation Trends and Restoration Prospects in the Karst Regions of Southwest China. Remote Sens. 2016, 8, 357. [Google Scholar] [CrossRef]
- Tong, X.; Wang, K.; Yue, Y.; Brandt, M.; Liu, B.; Zhang, C.; Liao, C.; Fensholt, R. Quantifying the effectiveness of ecological restoration projects on long-term vegetation dynamics in the karst regions of Southwest China. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 105–113. [Google Scholar] [CrossRef]









| Variables | Types | IMF1 | IMF2 | IMF3 | IMF4 | Residual |
|---|---|---|---|---|---|---|
| NDVI | Quasi-periods | 2.5 * | 5.8 | 11.2 | 25 | |
| Variance contribution rate (%) | 29.54 | 12.12 | 9.41 | 0.38 | 48.55 | |
| Temperature | Quasi-periods | 2.7 * | 5.5 * | 11.1 | 17.2 | |
| Variance contribution rate (%) | 56.4 | 25.84 | 8.79 | 0.58 | 9.55 | |
| Precipitation | Quasi-periods | 2.73 * | 6.50 | 15.67 * | 37 | |
| Variance contribution rate (%) | 52.21 | 14.23 | 28.87 | 1.42 | 3.9 |
| Region | Transfer Type | 1982–2015 | Before the Breakpoint | After the Breakpoint |
|---|---|---|---|---|
| Overall area | Farmland converted to forest | 1952.66 | 736.39 | 1287.15 |
| Forest converted to farmland | 1531.78 | 938.04 | 658.40 | |
| West area | Farmland converted to forest | 493.52 | 365.93 | 140.41 |
| Forest converted to farmland | 384.07 | 344.76 | 51.17 | |
| East area | Farmland converted to forest | 1454.34 | 369 | 1143.32 |
| Forest converted to farmland | 1144.45 | 591.11 | 490.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Liu, H.; Lin, Z.; Jiao, F.; Gong, H. Relationship of Abrupt Vegetation Change to Climate Change and Ecological Engineering with Multi-Timescale Analysis in the Karst Region, Southwest China. Remote Sens. 2019, 11, 1564. https://doi.org/10.3390/rs11131564
Xu X, Liu H, Lin Z, Jiao F, Gong H. Relationship of Abrupt Vegetation Change to Climate Change and Ecological Engineering with Multi-Timescale Analysis in the Karst Region, Southwest China. Remote Sensing. 2019; 11(13):1564. https://doi.org/10.3390/rs11131564
Chicago/Turabian StyleXu, Xiaojuan, Huiyu Liu, Zhenshan Lin, Fusheng Jiao, and Haibo Gong. 2019. "Relationship of Abrupt Vegetation Change to Climate Change and Ecological Engineering with Multi-Timescale Analysis in the Karst Region, Southwest China" Remote Sensing 11, no. 13: 1564. https://doi.org/10.3390/rs11131564
APA StyleXu, X., Liu, H., Lin, Z., Jiao, F., & Gong, H. (2019). Relationship of Abrupt Vegetation Change to Climate Change and Ecological Engineering with Multi-Timescale Analysis in the Karst Region, Southwest China. Remote Sensing, 11(13), 1564. https://doi.org/10.3390/rs11131564