Author Contributions
Conceptualization, B.M.S. and R.F.; Methodology, R.F.; Software, R.F.; Validation, Rong Fang and B.M.S.; Formal Analysis, R.F.; Investigation, R.F.; Resources, B.M.S.; Data Curation, R.F.; Writing-Original Draft Preparation, R.F.; Writing-Review & Editing, B.M.S.; Visualization, R.F.; Supervision, B.M.S.; Project Administration, B.M.S.; Funding Acquisition, B.M.S.
Figure 1.
LiDAR point clouds. (a) Rendering of the segmented sample tree point clouds; (b) point clouds of the entire plot and the locations of the 10 sample trees within the plot; (c) nadir view of the sample tree crowns.
Figure 1.
LiDAR point clouds. (a) Rendering of the segmented sample tree point clouds; (b) point clouds of the entire plot and the locations of the 10 sample trees within the plot; (c) nadir view of the sample tree crowns.
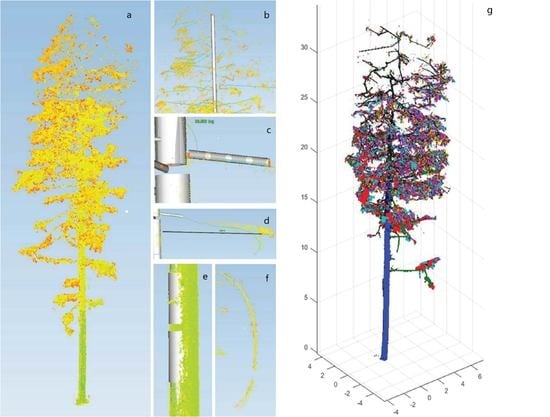
Figure 2.
Crown measurements in Cyclone. (a) The point clouds of a sample tree. (b) Incomplete point clouds of the top section of crown. (c) Cylinder models of a branch. Branch insertion angle is measured as the angle between the stem axis and branch cylinder axis. (d) Branch length measurements: sum of the length of line segments. The maximum horizontal distance from the stem is the branch projected distance. (e) Cylinder model of the stem. (f) Dead branch without leaves attaches on it.
Figure 2.
Crown measurements in Cyclone. (a) The point clouds of a sample tree. (b) Incomplete point clouds of the top section of crown. (c) Cylinder models of a branch. Branch insertion angle is measured as the angle between the stem axis and branch cylinder axis. (d) Branch length measurements: sum of the length of line segments. The maximum horizontal distance from the stem is the branch projected distance. (e) Cylinder model of the stem. (f) Dead branch without leaves attaches on it.
Figure 3.
An example of a quantitative structural models (QSM) created tree model. Different colors represent segments.
Figure 3.
An example of a quantitative structural models (QSM) created tree model. Different colors represent segments.
Figure 4.
The algorithm used to simulate individual trees crown using existing models.
Figure 4.
The algorithm used to simulate individual trees crown using existing models.
Figure 5.
Terrestrial laser scanning (TLS) identified individual branches by insertion height and azimuth.
Figure 5.
Terrestrial laser scanning (TLS) identified individual branches by insertion height and azimuth.
Figure 6.
Cumulative probability of branch insertion height. The p-values are for the Kolmogorov–Smirnov test used to compare the branch insertion height distribution of TreeQSM and Cyclone. The null hypothesis of the test is that two sets of values have the same distribution. Red dots mark the height at which the largest difference in the cumulative probability of the Cyclone and TreeQSM measured height is found.
Figure 6.
Cumulative probability of branch insertion height. The p-values are for the Kolmogorov–Smirnov test used to compare the branch insertion height distribution of TreeQSM and Cyclone. The null hypothesis of the test is that two sets of values have the same distribution. Red dots mark the height at which the largest difference in the cumulative probability of the Cyclone and TreeQSM measured height is found.
Figure 7.
Cumulative probability of branch azimuth. The p-values are for the Kolmogorov–Smirnov test used to compare the branch azimuth distributions estimated by TreeQSM and Cyclone. The null hypothesis of the test is that two sets of values have the same distribution. Red dots mark the azimuth at which the largest difference in the cumulative probability of the Cyclone and TreeQSM estimates are found.
Figure 7.
Cumulative probability of branch azimuth. The p-values are for the Kolmogorov–Smirnov test used to compare the branch azimuth distributions estimated by TreeQSM and Cyclone. The null hypothesis of the test is that two sets of values have the same distribution. Red dots mark the azimuth at which the largest difference in the cumulative probability of the Cyclone and TreeQSM estimates are found.
Figure 8.
Branch diameter estimates at insertion point by height section. (a) Comparison of branch diameter estimates of Cyclone and TreeQSM by height section; reference lines connect the mean of the aggregated estimates. (b) The difference of the branch diameter estimates between Cyclone and TreeQSM by height section.
Figure 8.
Branch diameter estimates at insertion point by height section. (a) Comparison of branch diameter estimates of Cyclone and TreeQSM by height section; reference lines connect the mean of the aggregated estimates. (b) The difference of the branch diameter estimates between Cyclone and TreeQSM by height section.
Figure 9.
Branch length estimates by height section. (a) Estimates for Cyclone and TreeQSM; reference lines connect the mean of the aggregated estimates. (b) Difference between the branch length estimates of Cyclone and TreeQSM. The dots represent the outliers identified with the quantile approach.
Figure 9.
Branch length estimates by height section. (a) Estimates for Cyclone and TreeQSM; reference lines connect the mean of the aggregated estimates. (b) Difference between the branch length estimates of Cyclone and TreeQSM. The dots represent the outliers identified with the quantile approach.
Figure 10.
Branch angle estimates by height section. (a) Estimates for Cyclone and TreeQSM; reference lines connect the mean of the aggregated estimates. (b) Difference between branch insertion angle estimates of Cyclone and TreeQSM by height section.
Figure 10.
Branch angle estimates by height section. (a) Estimates for Cyclone and TreeQSM; reference lines connect the mean of the aggregated estimates. (b) Difference between branch insertion angle estimates of Cyclone and TreeQSM by height section.
Figure 11.
(a–c) Mean and (d–f) maximum branch diameter of the 10 trees by diameter at breast height (DBH) class as a function of depth into the crown. The reference lines are second-order polynomial regression lines fit to the simulations and observations. Green and red lines are the simulated trees with second- and old-growth models, namely Ishii and Wilson (2001), and Maguire (1999) models. The shades represent the 95% confidence intervals of the simulated results of 10,000 trees.
Figure 11.
(a–c) Mean and (d–f) maximum branch diameter of the 10 trees by diameter at breast height (DBH) class as a function of depth into the crown. The reference lines are second-order polynomial regression lines fit to the simulations and observations. Green and red lines are the simulated trees with second- and old-growth models, namely Ishii and Wilson (2001), and Maguire (1999) models. The shades represent the 95% confidence intervals of the simulated results of 10,000 trees.
Figure 12.
(a–c) Mean and (d–f) maximum branch length of the 10 trees by DBH class as a function of depth into the crown. The reference lines are second order polynomial regression lines fit to the individual simulations and observations. Green and red lines are the simulated trees with second- and old-growth models, namely Ishii and Wilson (2001), and Maguire (1999) models. The shades represent the 95% confidence intervals of the simulated results of 10,000 trees.
Figure 12.
(a–c) Mean and (d–f) maximum branch length of the 10 trees by DBH class as a function of depth into the crown. The reference lines are second order polynomial regression lines fit to the individual simulations and observations. Green and red lines are the simulated trees with second- and old-growth models, namely Ishii and Wilson (2001), and Maguire (1999) models. The shades represent the 95% confidence intervals of the simulated results of 10,000 trees.
Figure 13.
Comparisons of quantitative structural models constructed with TreeQSM and Cyclone. Identification of some typical errors of structural models developed with TreeQSM. (a) Accurate stem model (silver cylinder) developed in Cyclone. (b) Inaccurate stem models developed with TreeQSM (blue cylinders). (c) A first-order branch was categorized as second-order in TreeQSM (red cylinder). (d) Cyclone rendering of the point clouds of the same branch shown in (c). (e) Stem models at the breast height of tree #3 in Cyclone. (f) Incorrect stem models at breast height of tree #3 in TreeQSM. Cylindrical models (blue cylinder) deviate from the stem point clouds resulting in the overestimation of DBH. (g) Accurate stem model (silver cylinder) constructed in Cyclone. (h) TreeQSM misidentified the stem points as the branch points and constructed models for a nonexistent branch (green cylinders shown in the right).
Figure 13.
Comparisons of quantitative structural models constructed with TreeQSM and Cyclone. Identification of some typical errors of structural models developed with TreeQSM. (a) Accurate stem model (silver cylinder) developed in Cyclone. (b) Inaccurate stem models developed with TreeQSM (blue cylinders). (c) A first-order branch was categorized as second-order in TreeQSM (red cylinder). (d) Cyclone rendering of the point clouds of the same branch shown in (c). (e) Stem models at the breast height of tree #3 in Cyclone. (f) Incorrect stem models at breast height of tree #3 in TreeQSM. Cylindrical models (blue cylinder) deviate from the stem point clouds resulting in the overestimation of DBH. (g) Accurate stem model (silver cylinder) constructed in Cyclone. (h) TreeQSM misidentified the stem points as the branch points and constructed models for a nonexistent branch (green cylinders shown in the right).
Figure 14.
Conceptual Douglas-fir tree architectures developed based on TreeQSM crown attribute estimates by DBH classes. (a). Conceptual crown structure of a tree with DBH of 52 cm, height of 42 m, and crown length of 27 m. (b). Conceptual crown structure of a tree with DBH of 63 cm, height of 40 m, and crown length of 21 m. (c). Conceptual crown structure of a tree with DBH of 106 cm, height of 45 m, and crown length of 20 m.
Figure 14.
Conceptual Douglas-fir tree architectures developed based on TreeQSM crown attribute estimates by DBH classes. (a). Conceptual crown structure of a tree with DBH of 52 cm, height of 42 m, and crown length of 27 m. (b). Conceptual crown structure of a tree with DBH of 63 cm, height of 40 m, and crown length of 21 m. (c). Conceptual crown structure of a tree with DBH of 106 cm, height of 45 m, and crown length of 20 m.
Figure 15.
Conceptual Douglas-fir tree architectures developed based on the Cyclone crown attribute estimates by the DBH classes. (a). Conceptual crown structure of a tree with DBH of 51 cm, height of 42 m, and crown length of 30 m. (b). Conceptual crown structure of a tree with DBH of 63 cm, height of 42 m, and crown length of 30 m. (c). Conceptual crown structure of a tree with DBH of 93 cm, height of 51 m, and crown length of 22 m.
Figure 15.
Conceptual Douglas-fir tree architectures developed based on the Cyclone crown attribute estimates by the DBH classes. (a). Conceptual crown structure of a tree with DBH of 51 cm, height of 42 m, and crown length of 30 m. (b). Conceptual crown structure of a tree with DBH of 63 cm, height of 42 m, and crown length of 30 m. (c). Conceptual crown structure of a tree with DBH of 93 cm, height of 51 m, and crown length of 22 m.
Table 1.
Summary of the involved crown attributes.
Table 1.
Summary of the involved crown attributes.
| Attribute | Abbreviation | Formula |
|---|
| Diameter at breast height | DBH | |
| Total Tree height | THT | |
| Branch diameter | BD | |
| Branch length | BL | |
| Branch insertion angle | α | |
| Branch azimuth | θ | |
| Height of branch i’s insertion point | | |
| Height of crown base | | |
| Crown Length | CL | |
| Branch depth into the crown | DINC | |
Table 2.
Summary of the number of branches by height section.
Table 2.
Summary of the number of branches by height section.
| Height of the Section (m) | Number of Branches |
|---|
| Cyclone | TreeQSM |
|---|
| <15 | 23 | 22 |
| 15–18 | 28 | 30 |
| 18–23 | 84 | 51 |
| 23–26 | 58 | 46 |
| 26–29 | 88 | 50 |
| 29–32 | 106 | 33 |
| 32–35 | 119 | 27 |
| 35–38 | 116 | 24 |
| 38–43 | 101 | 5 |
| >43 | 34 | 0 |
Table 3.
Semi-automatic (Cyclone) and automatic (TreeQSM) tree attribute estimates.
Table 3.
Semi-automatic (Cyclone) and automatic (TreeQSM) tree attribute estimates.
| Tree | DBH (cm) | Tree Height (m) | Crown Length (m) | No. of Branches (First Order) |
|---|
| Cyclone | TreeQSM | Cyclone | TreeQSM | Cyclone | TreeQSM | Cyclone | TreeQSM |
|---|
| 1 | 64 | 65 | 40.50 | 36.60 | 30.58 | 26.66 | 96 | 49 |
| 2 | 60 | 58 | 44.00 | 44.65 | 35.15 | 38.30 | 122 | 67 |
| 3 | 84 | 101 | 53.99 | 43.83 | 30.34 | 29.91 | 87 | 32 |
| 4 | 110 | 113 | 45.00 | 45.81 | 20.71 | 21.68 | 47 | 36 |
| 5 | 56 | 53 | 38.06 | 37.12 | 24.62 | 21.35 | 37 | 12 |
| 6 | 63 | 60 | 44.93 | 44.39 | 22.95 | 24.30 | 87 | 27 |
| 7 | 50 | 52 | 45.83 | 46.78 | 27.37 | 27.57 | 77 | 50 |
| 8 | 52 | 51 | 44.76 | 41.20 | 28.70 | 28.82 | 98 | 59 |
| 9 | 49 | 47 | 39.00 | 35.29 | 30.27 | 26.71 | 74 | 34 |
| 10 | 51 | 54 | 40.78 | 40.12 | 26.33 | 26.61 | 39 | 15 |
| Average | 63.9 | 65.4 | 43.69 | 41.58 | 27.7 | 27.19 | 76.4 | 38.1 |
Table 4.
Summary of mean branch diameter estimates by height section.
Table 4.
Summary of mean branch diameter estimates by height section.
| Height | Procedure | Difference | Absolute Difference |
|---|
| (m) | Cyclone (cm) | TreeQSM (cm) | (cm) | (%) | (cm) | (%) |
|---|
| <15 | 5.36 | 6.89 | −1.53 | −28.75 | 1.53 | 28.75 |
| 15–17 | 6.20 | 6.40 | −0.20 | −5.10 | 0.65 | 11.82 |
| 18–22 | 5.38 | 6.54 | −1.16 | −24.82 | 1.75 | 35.32 |
| 23–25 | 5.92 | 6.04 | −0.12 | −4.12 | 1.36 | 22.71 |
| 26–28 | 5.64 | 5.95 | −0.31 | −10.36 | 1.78 | 31.53 |
| 29–31 | 5.75 | 5.09 | 0.67 | 4.56 | 1.48 | 24.18 |
| 32–34 | 5.38 | 4.62 | 0.76 | 13.65 | 2.17 | 44.04 |
| 35–37 | 6.22 | 3.88 | 2.34 | 40.80 | 2.34 | 40.80 |
| 38–42 | 4.10 | 2.89 | 1.21 | 29.51 | 1.21 | 29.51 |
Table 5.
Difference in branch diameter estimates between Cyclone and TreeQSM as a function of height section, within a repeated measurements framework. Akaike information criterion (AIC) is defined as: , where k is the number of parameters, and is the maximum value of the likelihood function. Bayesian information criterion (BIC) is defined as: , where k is the number of parameters, n is the number of observations, and is the maximum value of the likelihood function.
Table 5.
Difference in branch diameter estimates between Cyclone and TreeQSM as a function of height section, within a repeated measurements framework. Akaike information criterion (AIC) is defined as: , where k is the number of parameters, and is the maximum value of the likelihood function. Bayesian information criterion (BIC) is defined as: , where k is the number of parameters, n is the number of observations, and is the maximum value of the likelihood function.
| Model Type | AIC | BIC |
|---|
| Unstructured | 161.8796 | 175.6169 |
| Repeated measures—AR(1) | 153.6215 | 168.8851 |
| Repeated measures—Compound Symmetry | 156.865 | 172.1286 |
Table 6.
Summary of branch length estimates by height section.
Table 6.
Summary of branch length estimates by height section.
| Height | Procedure | Difference | Absolute Difference |
|---|
| (m) | Cyclone (m) | TreeQSM (m) | (m) | (%) | (m) | (%) |
|---|
| <15 | 4.96 | 5.06 | −0.10 | 0.37 | 0.52 | 10.52% |
| 15–18 | 3.62 | 2.93 | 0.69 | 0.58 | 1.08 | 34.24% |
| 18–23 | 3.18 | 3.42 | −0.24 | −13.87 | 0.41 | 18.36% |
| 23–26 | 3.53 | 2.84 | 0.69 | 12.41 | 0.96 | 24.90% |
| 26–29 | 3.96 | 2.62 | 1.34 | 33.38 | 1.52 | 37.72% |
| 29–32 | 3.38 | 3.37 | 0.02 | −2.44 | 0.89 | 24.57% |
| 32–35 | 3.10 | 2.62 | 0.49 | 8.58 | 0.88 | 34.61% |
| 35–38 | 3.68 | 2.64 | 1.04 | 25.53 | 1.26 | 32.37% |
| 38–43 | 2.65 | 2.40 | 0.25 | 8.19 | 0.57 | 21.09% |
Table 7.
Summary of branch angle estimates by height section.
Table 7.
Summary of branch angle estimates by height section.
| Height Section | TreeQSM | Cyclone | Difference | Absolute Difference |
|---|
| (m) | Angle (°) | Angle (°) | (°) | (%) | (°) | (%) |
|---|
| <15 | 88.45 | 77.27 | −11.18 | −21.45 | 12.16 | 22.49 |
| 15–18 | 89.30 | 84.17 | −5.12 | −9.85 | 10.38 | 15.37 |
| 18–23 | 82.92 | 103.82 | 20.90 | 18.91 | 20.90 | 18.91 |
| 23–26 | 89.81 | 103.46 | 13.65 | 11.86 | 16.75 | 15.27 |
| 26–32 | 87.60 | 96.52 | 8.91 | 8.32 | 10.06 | 9.62 |
| 32–35 | 83.60 | 97.98 | 14.37 | 15.06 | 18.96 | 20.08 |
| 35–38 | 85.35 | 95.25 | 9.90 | 10.08 | 19.43 | 20.53 |
| 38–43 | 78.94 | 85.85 | 6.91 | 6.63 | 22.68 | 26.37 |