1. Introduction
Real-time synthetic aperture radar (SAR) imaging has always been a research focus in certain applications. Real-time imaging enhances the effectiveness and widens the application range of the SAR technique. In airborne SAR, real-time sensing plays an important role, and there are many well-established systems [
1,
2,
3,
4,
5] and techniques [
6,
7,
8,
9,
10,
11]. Real-time processing techniques are also available for unmanned aerial vehicle (UAV) SAR applications [
12,
13,
14]. For spaceborne SAR, because of its unique configuration and onboard computation capabilities, real-time SAR imaging systems and techniques are still being developed for both digital [
15,
16,
17] and optical [
18] methods.
For the purpose of implementing onboard real-time spaceborne SAR imaging, a set of Doppler parameters with high precision and accuracy must be calculated, and accurate position and velocity vectors are needed for the Doppler parameter calculation. In typical methods used to process SAR echo data, a high-accuracy orbit ephemeris is applied in the ground-based processing system, and state vectors, i.e., position and velocity vectors of the SAR satellite, are determined with high accuracy. However, this kind of high-accuracy orbit ephemeris is only generated hours, days, or even weeks after a single SAR observation [
19]. Thus, this kind of high-accuracy orbit ephemeris cannot be obtained during real-time SAR imaging. Nevertheless, we are still able to achieve onboard orbit determination using GNSS-based receivers and appropriate algorithms [
20,
21]. It is acknowledged that this approach to orbit determination has relatively low accuracy in the state vectors of SAR satellites compared with the high-accuracy orbit ephemeris. However, it remains the best, and possibly the only, onboard orbit determination method that is available for real-time SAR imaging.
SAR mission designers must account for the fact that errors in such onboard orbit determination data will adversely affect the quality of the SAR imaging product through inaccurate Doppler parameter calculation. Although estimation algorithms have been developed to generate the Doppler centroid and Doppler rate with high accuracy for SAR imaging, they are time-consuming in practice. Real-time spaceborne SAR imaging certainly does not belong on a mission that is not time-sensitive. The product of real-time SAR imaging may be the source data for other mission types, such as onboard deformation monitoring or target recognition. Given these requirements, the estimation algorithm should not be built into the processing workflow because of its long processing time. Thus, the concept of quadrature phase error (QPE) is introduced to evaluate the influence of onboard orbit determination errors on spaceborne SAR imaging products. The azimuth impulse response width of a SAR image has a certain relationship with QPE, and it provides a more intuitive evaluation standard of the errors.
Errors of an onboard orbit determination system are often given in the form of probabilities, along with the type of probability distributions and the corresponding parameters. The most common case for these errors is a normal distribution with an expected value of zero and a standard deviation
. Therefore, the probability distribution of QPE needs to be examined. In practice, there exist two major methods that have been applied to QPE analysis, i.e., the extreme value method and the numerical simulation method. The extreme value method is the simplest way to investigate QPE; it includes the maximum possible error in the calculation and ignores the probability distribution of the errors. This method faces challenges in revealing the QPE probability distribution, which means it only reflects the extreme situation in practice. For the numerical simulation methods, Monte Carlo simulations are often applied [
22]. However, this approach requires a huge number of generated error samples and repeated experiments.
In this paper, an analytical approximation model of the QPE introduced by orbit determination errors is proposed. With the a priori probability of the onboard orbit determination system and SAR satellite orbit elements, together with the observing geometry of the spaceborne SAR and appropriate approximations, a series of equations describing the parameters of the QPE probability distribution are presented. This analytical approximation model can provide approximation results at two granularities, i.e., the approximations with the satellite’s true anomaly as the independent variable and the approximations for all positions of the satellite during its entire orbit.
Following this section,
Section 2 describes the QPE analytical approximation model in general.
Section 3 derives the key variables in the analytical approximation model and reveals the appropriate approximations in the model. This is followed by the evaluation of the analytical approximation model by comparing it with numerical simulation results in
Section 4, and a related discussion is presented in
Section 5. Finally,
Section 6 provides a brief conclusion regarding the analytical approximation model.
2. Proposed Model: QPE Analytical Approximation Model
The QPE analytical approximation model requires four groups of parameters as input, i.e., the Earth’s physical parameters, the satellite platform orbit parameters, the SAR payload key parameters, and the a priori probability of the onboard orbit determination system. In this section, the coordinate systems, vector in the line-of-sight method, and QPE approximation method in the proposed model are described.
2.1. Coordinate Systems for Modeling
Two main coordinate systems are used in the derivation of the analytical approximation model. These two coordinate systems can be helpful in generating a clear description of the relative movement of the spaceborne SAR and the point of interest on the surface of the Earth.
2.1.1. Earth-Centered Inertial Coordinate System
Generally, the QPE calculation requires the position, velocity, and acceleration coordinates of the spaceborne SAR platform and the SAR antenna aiming point on the Earth’s surface, together with other variables. A widely used coordinate system in modeling the relative motion between the spaceborne SAR and the point of interest is the Earth-Centered Inertial (ECI) coordinate system. This system has an x-axis and z-axis aligned with the mean equinox and the celestial North Pole, respectively. The y-axis forms a right-handed coordinate system that joins the x-axis and z-axis.
In common practice, the onboard GNSS-based orbit determination system of a spaceborne satellite calculates its positions in a given coordinate system using the GNSS broadcast message [
21]. Each GNSS in service now has its own unique coordinate system, e.g., WGS 84 in GPS, CGCS2000 in BDS, and GTRF in Galileo. For modeling the orbit determination errors in the proposed analytical approximation model, all real-time-measured position and velocity coordinates of the spaceborne SAR platform are transformed into the ECI system in this paper.
2.1.2. Orbital Plane Coordinate System
The movement parameters of a spaceborne SAR satellite can be described in the orbital plane coordinate system. In this system, the Earth is located at one of the foci of the elliptical orbit, and the satellite can be regarded as a point. Polar coordinates are used to describe the movement parameters.
There exist six orbital elements that uniquely identify a specific orbit of the satellite: the semi-major axis a, eccentricity e, and true anomaly are used in the orbital plane coordinate system to determine the satellite’s movement at a certain time. The inclination i, the longitude of the ascending node , and the argument of periapsis are necessary to construct the transformation matrix between the orbital plane coordinate system and the ECI system.
The orbital plane coordinate system and the ECI system are summarized in
Figure 1.
2.2. Vector in the Line-of-Sight Method
In the analytical approximation model presented in this paper, the attitude errors of the spaceborne SAR satellite are not taken into consideration. The true value of the attitude of the platform is used in both the analytical approach and the following numerical verification.
With this assumption, the vector in the line-of-sight (VLS) method can be used to calculate the state vectors of the point of interest. The relative range from the SAR antenna phase center to the point of interest can be derived from the time delay of the echo signal. For spaceborne SAR geometry, the echo signal enters the receiver after several pulse repetition intervals (PRIs) until the moment of transmission, and then it is demodulated and sampled by the receiver. In each range profile of the sampled data, each sampled time delay can be determined by the index number of its range gate. The signal transmission delay from the antenna phase center to the sampling ADCs in the receiver can be accurately measured in the state-of-the-art spaceborne SAR system.
represents the delayed time of the echo of the point-of-interest signal from its transmission time, and
c represents the velocity of light, whose relative range is described by
A unit line-of-sight vector
in the ECI system can be created; it is perpendicular to the aperture of the SAR antenna and points to the surface of the Earth. The position vector
and velocity vector
of the point on the surface of the Earth at which the antenna points can be shown in stripmap SAR geometry as
in which
is the angular speed of the Earth’s rotation.
Because there are errors in the satellite’s position and velocity measurements from the onboard GNSS-based orbit determination system, the calculated and will also contain errors at the same time. The relative range remains unaffected because errors exist in measurements while the real geometry remains unchanged, which means that the time delay remains equal to the accuracy value.
2.3. QPE Approximation
QPE can be expressed in radians as [
23]
in which
is the Doppler rate of the echo signal, and
represents the integration time, also known as the synthetic-aperture time. In stripmap SAR geometry, the integration time is the time it takes the point of interest to enter and exit the entire 3 dB edge of the SAR antenna’s beam illumination.
The variables
,
, and
represent the relative position, velocity, and acceleration of the spaceborne SAR satellite, respectively. In the ECI system, for the antenna aiming point on the ground, the commonly used
expression in stripmap mode when the squint angle equals zero is
The
expression in Equation (
5) is an approximation expression, and it can achieve high precision if more terms remain. In the analytical approximation model, only the first two terms in Equation (
5) are analyzed. This simplifies the model while retaining a relatively high precision.
The orbit determination system measurements contain errors, which will lead to errors in
,
, and
. The terms that define the differences between the state vectors derived from measurements and the true state vectors are
where the subscript
e indicates that the vectors contain measurement errors. Thus, the difference between the measured
and true
value is
The parameter
in Equation (
5) is often used to determine the precise value for SAR raw data simulation or imaging algorithms. For the approximate expression of QPE, considering the magnitude of each term in
, some terms can be omitted while still achieving an acceptable approximation of QPE. The VLS method in
Section 2.2 maintains the real value of the relative range
. Thus, Equation (
4) combined with Equation (
9) gives the QPE approximation expression
For convenience, the terms and are named velocity and acceleration vector term in the following sections.
The approximation of QPE in Equation (
10) is the basis of the QPE analytical approximation function and maximum QPE derivation.
3. Key Variables in the Analytical Approximation Model
For a given true anomaly
, the distance between the satellite and the Earth’s center is
where
in Equation (
11) is the semi-latus rectum of the elliptic orbit. The position, velocity, and acceleration vectors of the satellite in the orbital plane (OP) are
where
is the standard gravitational parameter of the Earth.
The transformation matrix
is used to convert the vector in the orbital plane to the ECI system:
The parameter in results in rotation with the z-axis in the ECI system. Considering the geometry and the Earth’s ellipsoid reference, in the following discussion, we set for convenience, and this will not result in an error value in the QPE approximation.
The onboard orbit determination system measurements are given in ECI terms, which can be regarded as the true state vector plus an error vector. With the assumption that the measurement errors of the satellite’s position and velocity follow a normal distribution with an expected value of 0, the error vectors can be described as
Then, the state vector measurements of the satellite are
From Equations (
2), (
3), (
18) and (
19), the position vectors of the antenna aiming point are
With the help of Equations (
3), (
19) and (
20), the difference in the relative velocity from the satellite to the antenna aiming point can be given as
3.1. The Velocity Vector Term in the Approximate Doppler Rate
With Equation (
21), we have
. However, we still need the expression of
to calculate the velocity vector term
. It is worth recalling that we need the approximate Doppler rate expression. To calculate the velocity vector term in Equation (
10), we propose using the velocity vector of a satellite traveling in a circular orbit
in our analytical approximation model rather than using
. Thus, we have
The velocity vector term results in a Doppler rate difference by
Assuming that the variances of the position and velocity errors are the same standard deviation in the
x-,
y-, and
z-direction in the ECI system, i.e.,
and
, we can find the expected value and standard deviation of
by
We also need an approximate maximum value of the standard deviation of
to calculate the approximate maximum value of QPE. We suppose that
has a maximum value of
, and
3.2. True Anomaly
Equation (
21) gives the expression of difference vectors in the velocity vector term in Equation (
10). However, the difference vector in the acceleration vector term, i.e.,
, is given its expression with the help of true anomaly calculation.
The accurate acceleration vector term in the orbital plane is given in Equation (
14). True anomaly
should be calculated using the onboard-measured satellite’s position and velocity vectors. A common way to solve
is given in [
24]
where the
function returns an unambiguous result of
with a range of
. Obviously, the measured state vectors of the satellite
and
will result in a value of
that is not accurate. The probably distribution parameters of
should be determined in order to analyze the term
and its influence on QPE.
The detailed derivation is in
Appendix A. Here, the standard deviation and its maximum value of the difference between the calculated
and its accurate value
are given.
We assume that the variances of the position and velocity errors are the same standard deviation in the
x-,
y-, and
z-direction in the ECI system, i.e.,
and
. Equation (
29) can provide a good approximation when orbit eccentricity
e is rather small.
It is important to point out that
is not equal to the exact maximum value of
for
. This approximate maximum value is subsequently used to calculate the maximum value of QPE. With this assumption, it would be clearer to identify the core error terms of each variable. A more general expression without the assumption can be found in
Appendix A.
3.3. The Acceleration Vector Term in the Approximate Doppler Rate
With the expression
, the standard deviation of the difference between
calculated from state vector measurements and its true value is addressed, and the acceleration vector term can now can be dealt with. As
needs to be analyzed, the traditional yaw steering method [
25] is applied here.
where
N is the number of revolutions per day.
In this approximation model, we replace
with
only and ignore the errors in the target acceleration vector while keeping the satellite’s part. In the meantime,
is replaced by
in the row vector of Equation (
14). We can combine Equations (
14), (
18) and (
20) with
where
is the center off-nadir angle in stripmap SAR. The acceleration vector term results in a Doppler rate difference of
in which
In common SAR operations,
is usually small. Then, we have the following expansion without cubic and higher-order terms.
With the result from
Appendix B and Equations (
32)–(
34), the expected value and standard deviation of
are
Equation (
35) shows an interesting result. Instead of the expected zero value, we have
, which means there will be bias in the expected value of the Doppler rate
due to the calculated true anomaly. This bias can be and should be removed when calculating the Doppler parameters for the imaging algorithm.
However, we need the approximate maximum value of
. If we put aside the quadratic term of
in Equation (
36), the leftover part is modulated by
and
at each
point. When
x is relatively small,
. Combined with Equation (
30), we can ascertain that
. It can also be found that, from Equation (
28), if we take the appropriate approximation, then
. From these approximations,
in
when it reaches its maximum value
, and the very same
will also make
reach its maximum. Obviously, at this moment,
If
, then
together with
and
in Equation (
36). Thus, we have
3.4. Integration Time, Slant Range, and Approximate QPE
For a given SAR configuration and true anomaly, the integration time is used to calculate QPE, while the slant range contributes both to the integration time and QPE. In our proposed analytical approximation model for QPE, both the accurate and approximate integration time and slant range are considered. The former ones are applied to generate the approximate QPE with true anomaly as the independent variable, and the latter ones are merged into the maximum of the QPE calculation.
In the accurate calculation, the slant ranges are obtained by solving a quadratic equation:
where
6,378,137.000 m and
6,356,752.314 m are the semi-major axis and semi-minor axis of the ellipsoid reference in WGS 84, respectively. Then, the integration time is
In the approximate maximum QPE calculation, we use a slant range that is based on the circular Earth with a radius of
and
With the satellite’s velocity at apogee only instead of
, together with
a instead of
, we get the mean integration time.
Thus, we have the approximate expected value and standard deviation of QPE and its maximum expression:
where
and
are the standard deviations of QPE introduced by the velocity vector term and acceleration vector term, respectively.
5. Discussion
We designed an analytical approximation model of the QPE introduced by orbit determination errors. Our aim is to reduce the calculations and the processing time while revealing the core of the process by which error is transferred to QPE calculations. The technical parameter iteration period during early-stage development for an onboard real-time SAR imaging mission will benefit from the proposed methods.
SAR imaging requires the relative position, velocity, and acceleration vectors between the radar antenna and the targets to estimate the Doppler centroid and Doppler rate. Currently, in many ground-based processing systems for existing SAR missions, high-accuracy orbit determination data are applied to estimate the Doppler parameters. Such data have a time delay from the SAR raw data acquisition period, which is usually in the range of several hours or more. For real-time onboard SAR imaging missions, it is not realistic to wait for such high-accuracy orbit determination data to meet the “real-time” requirement. Real-time onboard orbit determination data have to be applied in the real-time onboard SAR imaging procedure. Current spaceborne SAR missions are usually based on a professional remote sensing satellite platform, and they are not as sensitive to perturbation. For a spaceborne SAR payload mounted on a small satellite platform to perform a constellation mission, such as MirrorSAR proposed by the DLR [
27], there will be some differences (i.e., it is not as steady as a large remote sensing satellite platform) in the movement of the actual target satellite. In these situations, the errors in the real-time onboard orbit determination data should be evaluated in order to examine whether they will jeopardize the new real-time SAR imaging mission concept.
There exist other terms of phase error in the context of SAR data processing [
28]. Besides QPE, there are linear, higher-order (more than cubic), sinusoidal, and random phase errors, among others. We selected QPE as the error of interest because it has defocus and loss-of-resolution effects on the image. An acceptable QPE should be seen as a tool that is used out of necessity but is not adequate for new SAR missions.
Research on the prediction of SAR imaging quality from the precision of the orbit ephemeris has been carried out [
29]: the upper limit expressions of multiple phase errors and their sensitivity to the orbit ephemeris covariance have been previously established. However, this method has two major limitations when applied to spaceborne real-time SAR imaging missions. Firstly, those upper limits only reflect the extreme situation, which will not always occur during a mission. We need to examine the whole situation of the phase error, as well as its probability form. Currently, the numerical simulation method can produce the probability of the phase error, but it is time-consuming. Secondly, in spaceborne real-time SAR imaging missions, it is impossible to get the orbit ephemeris directly, and it is calculated from onboard orbit determination data. The direct link between the precision of the onboard orbit determination data and the phase error in SAR imaging is still unclear. The proposed analytical approximation model is a potential solution to the two limitations above. With the precision of the onboard orbit determination system, which can be measured on the ground, the proposed analytical approximation model gives the direct QPE probability distribution result, which can simplify the analysis.
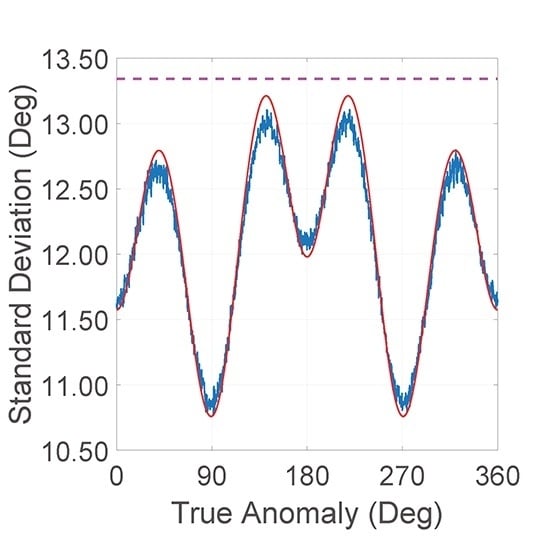
Compared with existing methods, the proposed analytical approximation model reduces the total calculations and processing time while revealing the core of the process by which errors are transferred to QPE calculations. This proposed analytical approximation model can reveal the QPE distribution, compared with the extreme value method mentioned in
Section 1. For the numerical simulation method, with
M error samples for each true anomaly calculation point and a total of
N true anomaly calculation points, the calculation complexity reaches
. It is important to point out that
M is usually a large number for better statistical results. No error sample set is generated in the analytical approximation model; thus, the calculation complexity is reduced. The QPE distribution result for
N true anomaly calculation points is
, and for the distribution parameters, the validated true anomaly
is
, which can significantly reduce the total calculation and processing time. Spaceborne real-time SAR imaging mission designers can quickly determine the maximum QPE with the help of only a calculator and the appropriate parameters. Therefore, this model will accelerate the technical parameter iteration procedure during the early-stage development of an onboard real-time SAR imaging mission and provide strong proof for the feasibility of such spaceborne real-time SAR missions.
There will always be some processing blocks in the design of a spaceborne SAR system. For each processing block, the errors introduced by processing must be limited for optimal performance of the whole system. From the design practice of the existing system, an azimuth impulse response width of
can be an acceptable limitation for a single processing block, which equals a QPE of no more than
[
23]. The results in
Section 4 are used here as an example. With the analytical approximation model, the result, and the three-sigma rule, it is clear that, with the simulation parameters given, if
is removed during the Doppler rate calculation, then the QPE introduced by the onboard orbit determination system will be less than 40.02
, with a probability of 99.73%. This result equals an azimuth impulse response width of less than 2%, with a probability of 99.73%.
In its current form, the proposed analytical approximation model is given when the attitude error is ignored; i.e., the orbit determination error and the attitude error of the platform are decoupled. The next generation of the analytical approximation model will take the attitude error into consideration in order to examine the coupled relationship. In addition, for spaceborne bistatic real-time SAR imaging missions, a bistatic form of the model will be needed. These two directions will be our future research topics.