A Novel Hyperspectral Endmember Extraction Algorithm Based on Online Robust Dictionary Learning
Abstract
:1. Introduction
- We model the hyperspectral endmember extraction problem as an online robust dictionary learning problem, and use more robust loss as the fidelity term in the objective function to improve the adaptability to noise.
- Considering the non-smoothness of the objective function in the proposed EEORDL, we minimize several quadratic objective functions iteratively to solve the online robust dictionary learning problem.
2. Materials and Methods
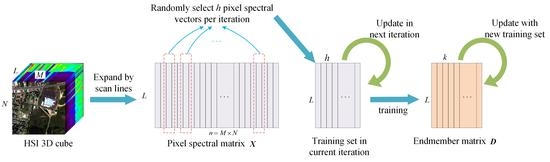
2.1. Sparse Model of Hyperspectral Endmember Extraction
2.2. Endmember Extraction Based on Online Robust Dictionary Learning
| Algorithm 1: Endmember extraction based on online dictionary learning (EEORDL) |
| Input: observed HSI , iterations , the number of the pixel spectral vectors used per iteration |
| Output: endmember matrix |
| 1 Preprocessing: Estimate the number of endmembers with HySime [26] |
| 2 Initialization: Initialize the endmember matrix with VCA; |
| 3 Given , initialize the abundance matrix with nonnegative least squares algorithm: |
| 4 for to do |
| 5 Draw randoml from |
| /* abundances update (robust sparse coding) */ |
| 6 for to do |
| 7 |
| 8 end for |
| /* endmembers update */ |
| 9 repeat |
| 10 for to do |
| 11 |
| 12 |
| 13 solve linear system |
| 14 |
| 15 end for |
| 16 until convergence |
| 17 end for |
| 18 return endmember matrix |
3. Experiments and Results
3.1. Evaluation Indexes
3.2. Synthetic Data
3.3. Real-World Data
3.3.1. Jasper Ridge Dataset
3.3.2. Urban Dataset
3.3.3. Cuprite Dataset
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, X.; Shi, Z.; Pan, B. ℓ0-based sparse hyperspectral unmixing using spectral information and a multi-objectives formulation. ISPRS J. Photogramm. Remote Sens. 2018, 141, 46–58. [Google Scholar] [CrossRef]
- Zou, Z.; Shi, Z. Hierarchical Suppression Method for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 330–342. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X.; Shi, T.; Zhang, N.; Zhu, X. CoinNet: Copy Initialization Network for Multispectral Imagery Semantic Segmentation. IEEE Geosci. Remote Sens. Lett. 2018, 16, 816–820. [Google Scholar] [CrossRef]
- Liu, S.C.; Bruzzone, L.; Bovolo, F.; Du, P.J. Unsupervised Multitemporal Spectral Unmixing for Detecting Multiple Changes in Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2733–2748. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.K.; Bioucas-Dias, J.M.; Chan, T.H.; Gillis, N.; Chi, C.Y. A Signal Processing Perspective on Hyperspectral Unmixing: Insights from Remote Sensing. IEEE Signal Process. Mag. 2014, 31, 67–81. [Google Scholar] [CrossRef]
- Feng, R.; Wang, L.; Zhong, Y. Least Angle Regression-Based Constrained Sparse Unmixing of Hyperspectral Remote Sensing Imagery. Remote Sens. 2018, 10, 1546. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Sparse Unmixing of Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2014–2039. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Le, W. Linear Spatial Spectral Mixture Model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3599–3611. [Google Scholar] [CrossRef]
- Chang, C.I.; Plaza, A. A Fast Iterative Algorithm for Implementation of Pixel Purity Index. IEEE Geosci. Remote Sens. Lett. 2006, 3, 63–67. [Google Scholar] [CrossRef]
- Nascimento, J.M.P.; Dias, J.M.B. Vertex component analysis: A Fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Winter, M.E. N-FINDR: An Algorithm for Fast Autonomous Spectral Endmember Determination in Hyperspectral Data. Proc. SPIE 1999, 3753, 266–275. [Google Scholar] [CrossRef]
- Yao, S.; Zeng, W.; Wang, N.; Chen, L. Validating the performance of one-time decomposition for fMRI analysis using ICA with automatic target generation process. Magn. Reson. Imaging 2013, 31, 970–975. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.C.; Lo, C.S.; Chang, C.L. Improved Process for Use of a Simplex Growing Algorithm for Endmember Extraction. IEEE Geosci. Remote Sens. Lett. 2009, 6, 523–527. [Google Scholar] [CrossRef]
- Li, J.; Agathos, A.; Zaharie, D.; Bioucas-Dias, J.M.; Li, X. Minimum Volume Simplex Analysis: A Fast Algorithm for Linear Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5067–5082. [Google Scholar] [CrossRef]
- Miao, L.; Qi, H. Endmember Extraction from Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization. IEEE Trans. Geosci. Remote Sens. 2007, 45, 765–777. [Google Scholar] [CrossRef]
- Li, J.; Bioucasdias, J.M.; Plaza, A.; Lin, L. Robust Collaborative Nonnegative Matrix Factorization for Hyperspectral Unmixing (R-CoNMF). IEEE Trans. Geosci. Remote Sens. 2016, 54, 6076–6090. [Google Scholar] [CrossRef]
- Zare, A.; Gader, P.; Bchir, O.; Frigui, H. Piecewise Convex Multiple-Model Endmember Detection and Spectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2853–2862. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Y.; Li, F.; Xin, L.; Huang, P. Sparse Dictionary Learning for Blind Hyperspectral Unmixing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 578–582. [Google Scholar] [CrossRef]
- Song, X.; Wu, L.; Hao, H. Blind hyperspectral sparse unmixing based on online dictionary learning. In Proceedings of the Image and Signal Processing for Remote Sensing XXIV, Berlin, Germany, 10–13 September 2018; p. 107890. [Google Scholar] [CrossRef]
- Qu, Y.; Qi, H. uDAS: An Untied Denoising Autoencoder With Sparsity for Spectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1698–1712. [Google Scholar] [CrossRef]
- Andrew, W.; John, W.; Arvind, G.; Zihan, Z.; Hossein, M.; Yi, M. Toward a practical face recognition system: Robust alignment and illumination by sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 372. [Google Scholar] [CrossRef]
- Lu, C.; Shi, J.; Jia, J. Online Robust Dictionary Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, X.; Cham, W.K. Background Subtraction via Robust Dictionary Learning. EURASIP J. Image Video Process. 2011, 2011, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Bissantz, N.; Dümbgen, L.; Munk, A.; Stratmann, B. Convergence analysis of generalized iteratively reweighted least squares algorithms on convex function spaces. Tech. Rep. 2008, 19, 1828–1845. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M.P. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Iordache, M.-D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, C.; Xiang, S.; Zhu, F. Robust Hyperspectral Unmixing with Correntropy-Based Metric. IEEE Trans. Image Process. 2015, 24, 4027–4040. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Zhang, H.; Zhang, L. Sparsity-Regularized Robust Non-Negative Matrix Factorization for Hyperspectral Unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4267–4279. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, Y.; Zhang, L.; Xu, Y. Spatial Group Sparsity Regularized Nonnegative Matrix Factorization for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6287–6304. [Google Scholar] [CrossRef]












| SNR (dB) | Index | VCA | PCOMMEND | MVCNMF | RCoNMF | EEODL | EEORDL |
|---|---|---|---|---|---|---|---|
| 35 | SAD(deg) | 0.3638 | 1.153 | 0.2452 | 1.792 | 0.5196 | 0.2618 |
| SID | 9.992 × 10−5 | 1.036 × 10−3 | 9.160 × 10−5 | 4.803 × 10−3 | 2.660 × 10−4 | 5.861 × 10−5 | |
| RMSE | 7.995 × 10−4 | 4.890 × 10−3 | 2.994 × 10−4 | 2.900 × 10−3 | 1.108 × 10−3 | 3.589 × 10−4 | |
| SRE(dB) | 24.04 | 17.54 | 27.76 | 17.60 | 22.19 | 27.13 | |
| 30 | SAD(deg) | 0.7552 | 1.555 | 0.5469 | 2.281 | 0.5993 | 0.4396 |
| SID | 5.623 × 10−4 | 3.083 × 10−3 | 3.174 × 10−4 | 7.843 × 10−3 | 2.674 × 10−4 | 1.315 × 10−4 | |
| RMSE | 2.204 × 10−3 | 1.691 × 10−2 | 1.102 × 10−3 | 5.123 × 10−3 | 2.822 × 10−3 | 1.087 × 10−3 | |
| SRE(dB) | 19.16 | 12.06 | 22.19 | 14.97 | 18.58 | 22.62 | |
| 25 | SAD(deg) | 0.9223 | 1.694 | 1.026 | 2.916 | 1.1567 | 0.6113 |
| SID | 8.529 × 10−4 | 3.413 × 10−3 | 1.200 × 10−3 | 1.160 × 10−2 | 1.119 × 10−3 | 2.615 × 10−4 | |
| RMSE | 5.362 × 10−3 | 1.817 × 10−2 | 2.912 × 10−3 | 8.702 × 10−3 | 1.030 × 10−2 | 3.085 × 10−3 | |
| SRE(dB) | 15.73 | 11.41 | 17.69 | 12.53 | 13.28 | 17.96 | |
| 20 | SAD(deg) | 2.092 | 1.857 | 1.937 | 2.977 | 1.166 | 0.6810 |
| SID | 4.534 × 10−3 | 4.285 × 10−3 | 4.812 × 10−3 | 1.180 × 10−2 | 1.072 × 10−3 | 2.989 × 10−4 | |
| RMSE | 1.382 × 10−2 | 2.356 × 10−2 | 8.034 × 10−3 | 1.724 × 10−2 | 1.061 × 10−2 | 7.457 × 10−3 | |
| SRE(dB) | 11.10 | 9.751 | 13.18 | 9.499 | 12.32 | 14.10 | |
| 15 | SAD(deg) | 5.354 | 2.818 | 7.571 | 3.650 | 2.039 | 1.854 |
| SID | 4.605 × 10−3 | 7.895 × 10−3 | 2.060 × 10−2 | 9.406 × 10−3 | 2.769 × 10−3 | 1.946 × 10−3 | |
| RMSE | 6.076 × 10−2 | 3.880 × 10−2 | 4.991 × 10−2 | 3.153 × 10−2 | 2.910 × 10−2 | 2.708 × 10−2 | |
| SRE(dB) | 5.178 | 7.111 | 6.212 | 6.908 | 8.360 | 8.834 |
| VCA | PCOMMEND | MVCNMF | RCoNMF | EEODL | EEORDL | |
|---|---|---|---|---|---|---|
| Time/s | 1.0 | 513.2 | 58.0 | 11.1 | 13.3 | 3.4 |
| Endmember | VCA | PCOMMEND | MVCNMF | RCoNMF | EEODL | EEORDL |
|---|---|---|---|---|---|---|
| Tree | 0.3228 | 0.1202 | 0.1705 | 0.2190 | 0.1897 | 0.1152 |
| Water | 0.2484 | 0.1889 | 0.9896 | 0.9460 | 0.2342 | 0.1105 |
| Dirt | 0.2263 | 0.1538 | 0.1567 | 0.1305 | 0.1601 | 0.1169 |
| Road | 0.2657 | 0.1120 | 0.1033 | 0.0546 | 0.0603 | 0.0502 |
| Mean | 0.2658 | 0.1437 | 0.3550 | 0.3375 | 0.1611 | 0.0982 |
| Endmember | VCA | PCOMMEND | MVCNMF | RCoNMF | EEODL | EEORDL |
|---|---|---|---|---|---|---|
| Asphalt | 0.1331 | 0.1055 | 0.1840 | 0.2450 | 0.1770 | 0.0999 |
| Grass | 0.3982 | 0.4568 | 0.5130 | 0.6206 | 0.3893 | 0.1258 |
| Tree | 0.0848 | 0.0541 | 0.1594 | 0.3587 | 0.1799 | 0.0530 |
| Roof | 0.1676 | 0.1135 | 0.1142 | 0.1640 | 0.2795 | 0.1075 |
| Mean | 0.1959 | 0.1825 | 0.2427 | 0.3347 | 0.2564 | 0.0966 |
| Endmember | VCA | PCOMMEND | MVCNMF | RCoNMF | EEODL | EEORDL |
|---|---|---|---|---|---|---|
| Alunite GDS84 Na03 | 0.1069 | 0.1331 | 0.1070 | 0.0889 | 0.1158 | 0.0864 |
| Andradite | 0.0782 | 0.0726 | 0.1018 | 0.2864 | 0.0791 | 0.0718 |
| Buddingtonite GDS85 D-206 | 0.2019 | 0.1661 | 0.2189 | 0.3351 | 0.2373 | 0.1656 |
| Dumortierite | 0.1375 | 0.0894 | 0.1804 | 0.1517 | 0.0881 | 0.0880 |
| Kaolinite KGa-2 (pxyl) | 0.2642 | 0.1118 | 0.3588 | 0.1072 | 0.2560 | 0.1121 |
| Kaolin/Smect KLF508 85%K | 0.0759 | 0.0893 | 0.0942 | 0.1471 | 0.1309 | 0.0906 |
| Muscovite IL107 | 0.1485 | 0.1217 | 0.1637 | 0.0705 | 0.1260 | 0.1216 |
| Montmorillonite+Illi CM37 | 0.1035 | 0.0605 | 0.1252 | 0.0727 | 0.1011 | 0.0600 |
| Nontronite SWa-1.a | 0.1072 | 0.1163 | 0.1776 | 0.1079 | 0.1551 | 0.1164 |
| Kaolin/Smect H89-FR-5 30K | 0.0817 | 0.0820 | 0.0987 | 0.0947 | 0.1574 | 0.0795 |
| Sphene | 0.0658 | 0.0543 | 0.0685 | 0.2036 | 0.0626 | 0.0539 |
| Chalcedony CU91-6A | 0.0666 | 0.0720 | 0.0737 | 0.4807 | 0.0639 | 0.0748 |
| Mean | 0.1198 | 0.0974 | 0.1474 | 0.1789 | 0.1311 | 0.0934 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Wu, L. A Novel Hyperspectral Endmember Extraction Algorithm Based on Online Robust Dictionary Learning. Remote Sens. 2019, 11, 1792. https://doi.org/10.3390/rs11151792
Song X, Wu L. A Novel Hyperspectral Endmember Extraction Algorithm Based on Online Robust Dictionary Learning. Remote Sensing. 2019; 11(15):1792. https://doi.org/10.3390/rs11151792
Chicago/Turabian StyleSong, Xiaorui, and Lingda Wu. 2019. "A Novel Hyperspectral Endmember Extraction Algorithm Based on Online Robust Dictionary Learning" Remote Sensing 11, no. 15: 1792. https://doi.org/10.3390/rs11151792
APA StyleSong, X., & Wu, L. (2019). A Novel Hyperspectral Endmember Extraction Algorithm Based on Online Robust Dictionary Learning. Remote Sensing, 11(15), 1792. https://doi.org/10.3390/rs11151792