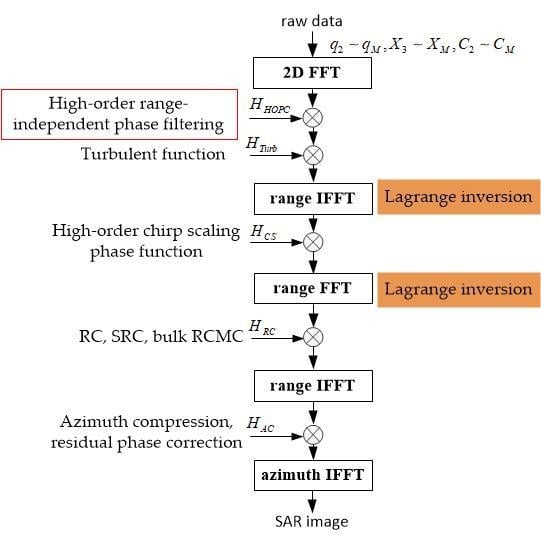
1. Introduction
Higher spatial resolution is an important development direction of synthetic aperture radar (SAR). Recent SAR systems are capable of resolutions in the decimeter regime. This requires the usage of large range bandwidth and wide azimuth beamwidth. The high-resolution, together with the all-weather day-and-night imaging capabilities, is turning SAR into an ideal tool for regular mapping and monitoring applications [
1,
2]. Moreover, microwaves can penetrate into vegetation and even the ground up to a certain depth [
3]. The penetration capabilities depend on the carrier frequencies as well as on the complex dielectric constants, densities and conductivities of the observed targets. The high frequencies, like the X-band (8–12 GHz), show typically a high attenuation and are mainly backscattered on the top of the vegetation. Low frequencies, like P- and L-band (0.23∼1 GHz and 1∼2 GHz, respectively) [
4], usually penetrate deep into vegetation, snow and ice. A high-resolution low frequency SAR system refers to a SAR system which operates with a low frequency (P- or L-band) signal with a large fractional bandwidth (>0.2, i.e., the ultra-wideband SAR [
2,
5,
6,
7,
8]) and a wide antenna beamwidth (corresponding to high azimuth resolution in the decimeter regime). The fractional bandwidth is defined by the ratio of the signal bandwidth to the center frequency. The combination of low frequency with large bandwidth and wide beam allows SAR to obtain high-resolution images of concealed targets, with the capability of penetrating the ground or foliage surface, thus it has broad applications for both military and civil purposes in recent years [
9,
10,
11,
12]. However, the large fractional bandwidth and long azimuth integration time used in high-resolution low frequency SAR bring new challenges to get high-quality images by the conventional image formation.
A crucial problem is the serious coupling between the range and azimuth frequencies in the phase of high-resolution low frequency SAR transfer function [
13]. In two-dimension (2D) frequency domain, the phase is range-dependent and can be decomposed into two parts: the range-independent terms and the range-dependent terms. Different algorithms make different approximations of these two parts. At low frequencies, many of the simplifying assumptions made by traditional algorithms are not valid, such as range-Doppler algorithm [
14] and chirp scaling algorithm (CSA) [
15], resulting in serious image degradations as blurring and resolution loss. The problem stems from high-order range-azimuth phase coupling. Several approaches have been used in the processing of this type of SAR system. The time-domain algorithms and the wavenumber-domain Omega-K (
) algorithm [
16,
17,
18] are two common options. The time-domain algorithms, often referred to as backprojection (BP) class algorithms [
19], are most accurate and can easily adapt to all SAR configurations. Due to their computational complexity and the poor ability to integrate accurate autofocus algorithm into its imaging process, their use is restricted. The
algorithm is an ideal solution without approximation in range cell migration (RCM) correction, which can focus data up to very high-resolution values regardless of their azimuth and range bandwidth. However, it is only applicable to spaceborne SAR data with a straight sensor trajectory and can only perform the range-independent motion compensation (MoCo). In addition, the Stolt interpolation makes it to be time-consuming. The extended Omega-K algorithm (EOKA) [
20,
21] is proposed to integrate the high precise range-dependent MoCo but it is still inefficient due to the Stolt interpolation.
For efficiency reasons, the chirp scaling class algorithms are still attractive. Efforts have been made to modify the CSA to process the low frequency SAR data. Without the interpolation, the chirp scaling class algorithms are effective and phase-preserving. The nonlinear chirp scaling algorithm (NCSA) [
13] is proposed to take into account the cubic range-independent coupling phase and the range dependence of secondary range compression (SRC) term, which has better performance than CSA on processing the raw data of highly squint or low frequency SAR cases. Whereas the range dependence of cubic- and higher order terms are neglected. Some modified NCSAs are proposed in References [
22,
23,
24], which resolve the high-order range-independent coupling terms. However, the cubic and higher order range-dependent coupling terms are still neglected. Besides, the first order approximation of range frequency modulation (FM) rate will introduce a quadratic phase error in the spectrum and degrades the focusing quality of image. Thus, the range focusing depth is restricted, which shows that the NCSA may not be suitable for the high-resolution low frequency SAR processing. A helpful comparison of the BP class algorithm,
algorithm, EOKA and NCSA can be found in References [
22,
25]. In References [
26,
27], a generalized chirp scaling algorithm (GCSA) is developed for the SAR systems operating on wide bandwidths at low frequencies. The GCSA is an efficient arbitrary-order CSA that processes the data using the appropriate number of the approximation terms. Both the higher range-independent terms and range-dependent terms are considered. The GCSA efficiently extends the utility of frequency domain processing for high-resolution low frequency SAR systems. However, the imaging quality of GCSA also decreases as the fractional bandwidth get larger and beamwidth gets wider. In addition, the improvement of focus quality is not significant when the order is greater than 3rd and the edge targets of the range swath still have obvious degradation. Two main reasons lead to this phenomenon. One is that the residual coupling terms are still significant and the other is the error caused by the linear approximation of stationary phase point when solving the fast Fourier transform (FFT) expression. The linear approximation makes the range-dependent high-order phase terms not effectively compensated, even if a higher-order model is used.
The aim of this study is to overcome these two limits of GCSA and propose a more accurate approach than the GCSA for processing wide-swath, high-resolution low frequency SAR data. To our knowledge, the Lagrange inversion [
28,
29,
30,
31] gives the power series representation of the inverse of an analytic function, which is quite suitable for calculating the expression of stationary phase point. This paper utilizes Lagrange inversion to calculate a more precise expression of stationary phase point, while compensating for all range-independent coupling terms above 3rd order. In our approach, the high-order chirp scaling technique is extended to achieve the effect of the range-variant filtering required in high order phase terms. The experimental results show that the improved algorithm has a better focusing performance than the original GCSA. The resolution, sidelobe level and range focusing depth are significantly improved.
This paper is organized as follows. In
Section 2, the signal model of high-resolution low frequency SAR is analyzed and the limitations of existing GCSA are briefly described. Then, a principle to determine the required order of range-dependent coupling phase is presented. In
Section 3, an improved GCSA based on the Lagrange inversion theorem is introduced to focus the high-resolution low frequency SAR data. Focused results obtained by the conventional GCSA and the improved GCSA are presented and analyzed to verify our analysis in
Section 4. A discussion is givne in
Section 5. Finally, conclusions are drawn in
Section 6.
4. Experiment Results and Analysis
In this section, we provide some imaging results to demonstrate the performance of proposed algorithm and the analysis of principle. The system parameters are listed in
Table 1. The parameters of platform velocity, pulse duration and center slant range of each SAR system are set to the same value. The reference slant range is selected as the scene center slant range. The theoretical azimuth and range resolutions are evaluated by
and
=
. The maximum Doppler frequency can be expressed as
where
and
are the minimum signal wavelength and the maximum azimuth angle. The PRF must not be chosen less than two times of
. The range oversampling rate is set to 1.2.
Firstly, to investigate the effects of two improvements in the proposed algorithm, a P-band SAR with a center frequency of 600 MHz was simulated. The fractional bandwidth is set to 50% (corresponding to a range resolution of 0.44 m) and the beamwidth is set to 29° (corresponding to an azimuth resolution of 0.44 m). Nine targets are arranged in the illuminated scene along the azimuth center at different distances form the reference range with an interval of 200 m. The conventional GCSA in Reference [
26] is used in comparison with the proposed algorithm. According to the principle in
Section 2.3, the data is processed with a 6th order model. To highlight the effect of Lagrange inversion, the conventional GCSA with Lagrange inversion (ignoring the range-independent coupling terms above 6th order) is also used in comparison. The 2D focused images of targets at the ranges
,
m and
m are shown in
Figure 6. In these figures, contour maps donate the 2D focusing quality. To evaluate the quality of these images quantitatively, the resolution (Res), peak sidelobe ratio (PSLR) and integrated sidelobe ratio (ISLR) along the range and azimuth directions are presented in
Table 2. No wighting function or sidelobe control approach is used to obtain a fair comparison. Note that the ideal response is not completely symmetric in the range direction due to the significant range-azimuth coupling.
Figure 6a–c and
Table 2 illustrate that the conventional GCSA causes deterioration of the images. The images of three targets are defocused in two directions, even at the scene center targets. The Res, PSLR and ISLR degrade considerably. This issue becomes increasingly serious as the distance increases. This problem is caused by the residual high-order range-independent coupling terms and the phase error introduced by approximate of stationary phase point. As the fractional bandwidth increases, even the scene center point has a severe degradation. Especially, the asymmetric sidelobe in range dimension is obvious.
Figure 6d–f shows the imaging results obtained by the GCSA with Lagrange inversion. It can be seen that all three targets are effectively focused, which indicates that the Lagrange inversion can eliminate the range-dependent coupling terms. However, since the range-independent coupling terms above 6th order are neglected, the sidelobes in range direction are severe and the images have a certain quality degradation. The imaging results obtained by the proposed algorithm are shown in
Figure 6g–i, with better quality than
Figure 6d–f. From the quality indices presented in
Table 2, the imaging coherency is good over the entire swath. These benefits stem from the compensation of coupling terms above 6th order and Lagrange inversion.
To evaluate the accuracy of proposed algorithm better, we measure the Res and differential resolutions (DRES) [
32] at different slant range.
Figure 7 shows the Res and DRES of nine point targets processed in different algorithms. The references for the DRES measurements are the range and azimuth resolutions obtained by
algorithm. It can seen that the range and azimuth resolutions loss of GCSA is greater than 13% compared with the
algorithm but the resolutions loss of the proposed algorithm is less than 1%. We can conclude that the focusing performances of the proposed algorithm are much better than the ones of GCSA and closed to the ones of
algorithm. The image quality and focusing depth in range dimension are greatly improved.
Secondly, in order to better validate the performance of the proposed algorithm, the point scatterer was placed at the edge of the swath, where
= 2 km. A typical L-band SAR system with a center frequency of 1.36 GHz was simulated. The beamwidth is set to 11° (corresponding to an azimuth resolution of 0.5 m). The fractional bandwidth is set to 20%, 40%, 60% and 80%, respectively. According to Equation (
5), four sets of data are focused by the 3rd order, 4th order, 6th order and 7th order models, respectively.
Figure 8 shows the Res and DRES versus fractional bandwidth for the GCSA and proposed algorithm. The resolutions obtained by
algorithm are references. When the fractional bandwidth is 20%, both the GCSA and proposed algorithm can achieve good focusing performance. As the fractional bandwidth increases, the performance of GCSA drops dramatically. If the resolution loss threshold is 10%, the GCSA can only process the data where the fractional bandwidth is less than 30%. However, the proposed algorithm achieves nearly the theoretically resolutions for fractional bandwidths up to 80% for L-band. The resolution broadening is less than 1%, which shows the performance is greatly improved over that of the original GCSA.
Next, to illustrate the worst case shape of the proposed image of the point target,
Figure 9 illustrates the contour plots, range profiles and azimuth profiles of the processed images at 80% fractional bandwidth. In both figures, the contour maps denote the 2D focusing quality and the profiles represent the focusing quality along the azimuth and range directions. The measured parameters are shown in
Table 3. As can be seen, the results of GCSA in this case suffers form severe distortion and broadening. The signal in both range and azimuth are almost defocused. However, the proposed algorithm preserves the focusing performance. It is easy to recognize that the images obtained by the proposed algorithm are well focused, as are shown in
Figure 9d–f. The nearly theoretical values of spatial resolution, PSLR and ISLR are obtained, which demonstrates the validity of the proposed algorithm. The good performance is given by the high-order range-independent phase filtering and the Lagrange inversion, which greatly reduces the range-dependent phase error. By comparing the range and azimuth profiles, it is evident that the Lagrange inversion makes the range-dependent coupling terms effectively compensated. The focusing depth in range dimension is greatly improved. The improved algorithm is consistent with the conventional GCSA in terms of computational complexity but the focusing performance is significantly improved. The improved method provides an attractive solution for processing the low frequency large bandwidth and wide beamwidth SAR data.
Finally, to further test the analysis presented in this paper, a SAR real image (Longmen, Henan, China) is used as the input radar cross section to generate SAR echo. The center frequency of the transmitted signal is 400 MHz, the bandwidth is 250 MHz, the beamwidth is 25°, the velocity is 120 m/s, the PRF is 200 Hz, the pulse duration is 10 us and the center slant range is 10 km. The scene size is 3.0 km in range and 1.5 km in azimuth. The resolutions are 0.53 m in range and 0.76 m in azimuth. In the simulation, the input image is a real complex image. Each cell of the complex image is treated as a point scatterer (this actually contains the target signal and noise). No additional noise was added during the simulation.
Figure 10 shows the imaging results processed by the conventional GCSA and the improved algorithm.
As is shown in
Figure 10, at the center range region, the focusing quality of the two images is nearly the same. However, at the near and far range region, the texture character of the image obtained by improved GCSA is clearer than that obtained by conventional GCSA. It is obvious that better focusing results are obtained by the proposed method. The image has very high quality. The roads, rivers and farmland can be clearly distinguished. The edge scene along range dimension is well focused. It is evident that the range focusing depth is greatly improved.
In order to have a distinct contrast, three subregions marked by red solid rectangle are extracted and analyzed in detail. The zooms regions are shown in
Figure 11a–f. The entropy [
33,
34] of images is calculated to compare the focus quality and shown in
Table 4. It is generally acknowledged that SAR images with better quality focus have smaller entropy. It is easy to find that images obtained by proposed method have smaller entropy. Therefore, the effectiveness of proposed algorithm is again validated.
5. Discussion
The performance of the proposed algorithm is mainly limited by the approximation error of range FM rate
(Equation (
22)). This approximation will introduce a quadratic phase error (QPE) in the spectrum and degrades the quality of the image. In the CSA, the range dependence of SRC is neglected and the FM rate is calculated at the reference range
. The NCSA uses a linear approximation of the FM rate and the GCSA uses a 2nd order approximation model.
The QPE can be expressed as
From Equation (
8), we can see that the Taylor expansion is feasible only under the following condition
Let , this function is positively related to , , and negatively related to , . And , where is the pulse duration. The azimuth frequency varies within the following range , where PRF is the pulse repetition frequency. Thus, G is an even function about and inequality (37) actually implied condition . This inequality is satisfied in most L- and P-band SAR systems. However, as the center frequency decreases, the maximum azimuth frequency increases and the slant range increases, this inequality may not be satisfied. At this time, the Taylor approximation of range FM rate will introduce a large error and worsen the performance of algorithm.
It should be noted that
is required for all frequency domain approximation algorithms (such as the chirp scaling class and the range-Doppler class algorithms) [
14]. This is satisfied for a linear FM signal with a large time bandwidth product (TBP). The TBP is defined as the product of the pulse duration
and bandwidth
. For example, assuming the SAR system with a following parameters: center frequency
= 400 MHz, bandwidth
= 200 MHz, beamwidth
= 29°, velocity
= 100 m/s, pulse duration
= 2 us (TBP = 400), target slant range
= 12 km and center slant range
= 10 km.
Figure 12a shows the variation of
G with azimuth frequency
.
Figure 12c–e show the QPEs in zero-order, 1st-order and 2nd-order approximations, respectively. It can be seen that
G is not less than 1 at this time. Due to the existence of breakpoints, the QPEs of 1st-order and 2nd-order approximations are larger than zero-order approximation. The maximum QPE of 2nd-order model is about 5000°, which will seriously deteriorate the image quality.
Change the pulse duration
= 10 us (TBP = 2000), the variation of
G with azimuth frequency is show in
Figure 12b. The QPEs of different approximations are also shown in
Figure 12f–h.
G is far less than 1, meeting the inequality (37). At this time, the maximum QPE of 1st-order model is 230° and the maximum QPE of 2nd-order model is 14°, which has a limit effect on the imaging results.
By comparison, it can be concluded that the proposed algorithm has the best performance in frequency domain approximation algorithms when Equation (
37) is satisfied. If Equation (
37) is not satisfied, the performance of the approximation algorithm is degraded and the
algorithm and time-domain algorithms are a better choice. At the same time, it should be pointed out that most of the existing airborne SAR systems have a large TBP [
35,
36], which shows that the proposed algorithm still has a broad application prospects. In particular, the proposed algorithm can be applied to high-resolution highly squint SAR imaging, where the phase coupling is also severe.