Single Space Object Image Denoising and Super-Resolution Reconstructing Using Deep Convolutional Networks
Abstract
:1. Introduction
- We propose a method named SO-EVDSR. This method could remove cosmic-ray noise and enhance the spatial resolution of SO images in the meantime. It is the first time that a denoising and SR reconstruction method based on only one very deep convolutional network implemented in the SO images research field.
- This method combines the global residual learning and local residual learning. Experimental results show that our method performs better than several typical methods including some state-of-the-art methods in both quantitative measurements and visual effect.
2. Related Works
2.1. Cosmic-Ray and Denoising
2.2. Single Image Super-Resolution
3. Proposed Method
3.1. Problem Definition
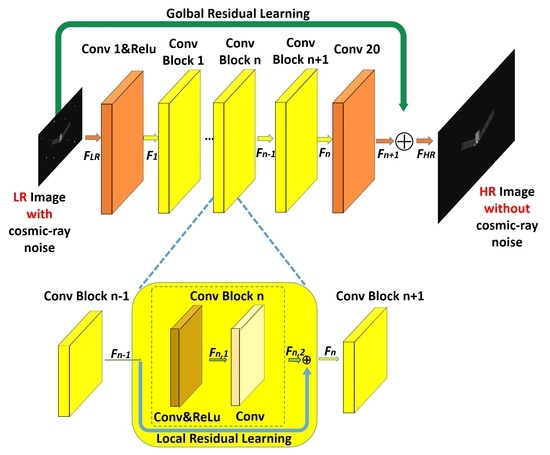
3.2. Proposed Network
3.2.1. Enhanced Very Deep Super-Resolution Network in Space Object Researching
3.2.2. Residual Learning in SO-EVDSR
4. Experiment
4.1. Dataset
4.2. Training Parameters
4.3. Results
4.3.1. Quantitative Measurements
4.3.2. Quantitative Results
4.3.3. Visual Comparison Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, Z.; Liu, L. Hyperspectral Image Super-Resolution Inspired by Deep Laplacian Pyramid Network. Remote Sens. 2018, 10, 1939. [Google Scholar] [CrossRef]
- Pouliot, D.; Latifovic, R.; Pasher, J.; Duffe, J. Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training. Remote Sens. 2018, 10, 394. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Hou, H.; Andrews, H. Cubic spline for image interpolation and digital filtering. IEEE Trans. Image Process. 1978, 26, 508–517. [Google Scholar]
- Dodgson, N. Quadratic interpolation for image resampling. IEEE Trans. Image Process. 1997, 6, 1322–1326. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Tsai, R. Multi-frame image restoration and registration. Adv. Comput. Vis. Image Process. 1984, 1, 317–339. [Google Scholar]
- Kim, S.; Bose, N.; Valenauela, H. Recursive reconstruction of high resolution image from noisy undersampled multiframes. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1013–1027. [Google Scholar] [CrossRef]
- Hayat, K. Super-Resolution via Deep Learning. arXiv 2017, arXiv:1706.09077. [Google Scholar]
- Timofte, R.; Rothe, R.; Gool, L.V. Seven ways to Improve Example-based Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1865–1873. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Zhuang, L.; Maaten, L. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image Super-Resolution Using Dense Skip Connections. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4799–4807. [Google Scholar]
- Mei, S.; Lin, X.; Ji, J.; Zhang, Y.; Wan, S.; Du, Q. Hyperspectral Image Spatial Super-Resolution via 3D Full Convolutional Neural Network. Remote Sens. 2017, 9, 1139. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3262–3271. [Google Scholar]
- Huang, J.; Singh, A.; Ahuja, N. Single image super resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Kim, K.; Kwon, Y. Single-image super-resolution using sparse regression and natural image prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar] [PubMed]
- Jiang, K.; Wang, Z.; Yi, P.; Jiang, J.; Xiao, J.; Yao, Y. Deep Distillation Recursive Network for Remote Sensing Imagery SuperResolution. Remote Sens. 2018, 10, 1700. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.; Lee, K. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 142–149. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Windhorst, R.; Franklin, B.; Neuschaefer, L. Removing Cosmic-ray Hits from Multiorbit HST Wide Field Camera Images. Publ. Astron. Soc. Pac. 1994, 106, 798–806. [Google Scholar] [CrossRef]
- Zhu, Z.; Ye, Z. Detection of Cosmic-ray Hits for Single Specroscopic CCD Images. Publ. Astron. Soc. Pac. 2008, 120, 814–820. [Google Scholar] [CrossRef]
- Van Dokkum, P. Cosmic-Ray Rejection by Laplacian Edge Detection. Publ. Astron. Soc. Pac. 2000, 113, 1420–1429. [Google Scholar] [CrossRef]
- Pych, W. A Fast Algorithm for Cosmic-ray Removal from Single Images. Publ. Astron. Soc. Pac. 2004, 116, 148–153. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.; Liao, Q. Deep Learning for Single Image Super-Resolution: A Brief Review. arXiv 2019, arXiv:1808.03344. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S. Deep Learning for Image Super-resolution: A Survey. arXiv 2019, arXiv:1902.06068. [Google Scholar]
- Jain, V.; Seung, H. Natural image denoising with convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–10 December 2008; pp. 769–776. [Google Scholar]
- Mao, X.; Shen, C.; Yang, Y. Image Restoration Using Convolutional Auto-encoders with Symmetric Skip Connections. arXiv 2016, arXiv:1606.08921. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.; Lee, K. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Xu, W.; Xu, G.; Wang, Y.; Sun, X.; Lin, D.; Wu, Y. Deep Memory Connected Neural Network for Optical Remote Sensing Image Restoration. Remote Sens. 2018, 10, 1893. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar]
- Zhang, H.; Liu, Z.; Jiang, Z. Buaa-sid1.0 space object image dataset. Spacecr. Recovery Remote. Sens. 2010, 31, 65–71. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale Structural Similarity for Image Quality Assessment. Signals Syst. Comput. 2004, 2, 1398–1402. [Google Scholar]
- Kwan, C.; Larkin, J.; Budavari, B.; Chou, B.; Shang, E.; Tran, T.D. A Comparison of Compression Codecs for Maritime and Sonar Images in Bandwidth Constrained Applications. Computers 2019, 8, 32. [Google Scholar] [CrossRef]
- Ochoa, H.D.; Rao, K.R. Discrete Cosine Transform, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Wang, Z.; Bovik, A.C. A universal image quality index. IEEE Signal Process. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Silvestri, F.; Egiazarian, K.; Carli, M.; Astola, J.; Lukin, V. On between-coefficient contrast masking of DCT basis functions. In Proceedings of the Third International Workshop on Video Processing and Quality Metrics for Consumer Electronics VPQM-07, Scottsdale, AZ, USA, 25–26 January 2007. [Google Scholar]
- Lebrun, M. An analysis and implementation of the BM3D image denoising method. Image Process. Line 2012, 2, 175–213. [Google Scholar] [CrossRef]
- Kwan, C.; Zhou, J. Method for Image Denoising. U.S. Patent US9159121B2, 13 October 2015. [Google Scholar]





















| Block | Layer | Name | Conv<Receptive Field Size>-<Number of Channels>-<Number of Filter> | Parameters |
|---|---|---|---|---|
| 1 | Conv | Conv3-1-64 | 1664 | |
| Relu | ||||
| 1 | 2 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 3 | Conv | Conv3-64-64 | 102,464 | |
| 2 | 4 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 5 | Conv | Conv3-64-64 | 102,464 | |
| 3 | 6 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 7 | Conv | Conv3-64-64 | 102,464 | |
| 4 | 8 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 9 | Conv | Conv3-64-64 | 102,464 | |
| 5 | 10 | Conv | Conv3-64-64 | 102,464 |
| Relu | 102,464 | |||
| 11 | Conv | Conv3-64-64 | 102,464 | |
| 6 | 12 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 13 | Conv | Conv3-64-64 | 102,464 | |
| 7 | 14 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 15 | Conv | Conv3-64-64 | 102,464 | |
| 8 | 16 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 17 | Conv | Conv3-64-64 | 102,464 | |
| 9 | 18 | Conv | Conv3-64-64 | 102,464 |
| Relu | ||||
| 19 | Conv | Conv3-64-64 | 102,464 | |
| 20 | Conv | Conv3-1-64 | 102,464 |
| Method | Scale | MSE | PSNR | SSIM | HVS | HVSm |
|---|---|---|---|---|---|---|
| Bicubic | 2 | 4.810885296 | 41.30855358585935 | 0.9999984940625836 | 54.1835 | 54.2532 |
| 3 | 9.004434909 | 38.58623897872875 | 0.9999963947901308 | 52.2901 | 52.3281 | |
| 4 | 13.07634938 | 36.96593844957169 | 0.9999929499766917 | 50.8295 | 51.0292 | |
| SRCNN | 2 | 3.087851266 | 43.23423987529352 | 0.9999989854654752 | 56.5810 | 56.7858 |
| 3 | 6.815264731 | 39.79597630702207 | 0.9999972759376027 | 54.6213 | 54.9024 | |
| 4 | 10.10653004 | 38.08478289567298 | 0.9999954949789307 | 52.0198 | 52.2285 | |
| VDSR | 2 | 2.518198065 | 44.11990474992009 | 0.9999992553686302 | 57.0211 | 57.2354 |
| 3 | 5.540032111 | 40.69568078908413 | 0.9999982028334025 | 55.2018 | 55.3811 | |
| 4 | 8.284960877 | 38.94789898927323 | 0.9999968440793972 | 52.7028 | 53.0285 | |
| DRCN | 2 | 2.452489995 | 44.23473116546864 | 0.9999992569876331 | 57.8302 | 58.0522 |
| 3 | 5.527730285 | 40.70533516546694 | 0.9999982135434648 | 56.0238 | 57.2419 | |
| 4 | 8.263899739 | 38.95895321354315 | 0.9999968452134436 | 53.5229 | 53.9219 | |
| DMCN | 2 | 2.370692141 | 44.38205200938572 | 0.9999992858920935 | 59.3410 | 60.1925 |
| 3 | 5.31803133 | 40.87329469327502 | 0.9999982947593297 | 56.6815 | 58.2859 | |
| 4 | 8.124998092 | 39.03257093209752 | 0.9999969012845702 | 54.0283 | 54.8921 | |
| SO-EVDSR | 2 | 2.263607982 | 44.58279144085883 | 0.9999993199209739 | 61.4168 | 62.0269 |
| 3 | 5.08946923 | 41.06407867788109 | 0.9999983700995432 | 59.0214 | 60.1920 | |
| 4 | 7.891428243 | 39.15924749054321 | 0.9999969575852177 | 57.1832 | 57.9237 |
| Method | Scale | PSNR |
|---|---|---|
| Only Using GRL(VDSR) | 2 | 44.11990474992009 |
| 3 | 40.69568078908413 | |
| 4 | 38.94789898927323 | |
| Only Using LRL | 2 | 44.00266113315757 |
| 3 | 40.42742178926535 | |
| 4 | 38.63971533159192 | |
| SO-EVDSR | 2 | 44.58279144085883 |
| 3 | 41.06407867788109 | |
| 4 | 39.15924749054321 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, X.; Su, X.; Shen, J.; Jin, H. Single Space Object Image Denoising and Super-Resolution Reconstructing Using Deep Convolutional Networks. Remote Sens. 2019, 11, 1910. https://doi.org/10.3390/rs11161910
Feng X, Su X, Shen J, Jin H. Single Space Object Image Denoising and Super-Resolution Reconstructing Using Deep Convolutional Networks. Remote Sensing. 2019; 11(16):1910. https://doi.org/10.3390/rs11161910
Chicago/Turabian StyleFeng, Xubin, Xiuqin Su, Junge Shen, and Humin Jin. 2019. "Single Space Object Image Denoising and Super-Resolution Reconstructing Using Deep Convolutional Networks" Remote Sensing 11, no. 16: 1910. https://doi.org/10.3390/rs11161910
APA StyleFeng, X., Su, X., Shen, J., & Jin, H. (2019). Single Space Object Image Denoising and Super-Resolution Reconstructing Using Deep Convolutional Networks. Remote Sensing, 11(16), 1910. https://doi.org/10.3390/rs11161910