Multi-Sensor Geodetic Observations and Modeling of the 2017 Mw 6.3 Jinghe Earthquake
Abstract
:1. Introduction
2. Regional Tectonic Settings and Dataset
2.1. Tectonic Setting
2.2. SAR Imagery and Auxiliary Datasets
3. Coseismic Displacement Field Reconstruction
3.1. Processing Strategy of Multi-Temporal and Multi-Geometric Interferogram Stacks
3.2. Sentinel-1 Interferogram Processing
3.3. ALOS2 PALSAR2 Interferogram Processing
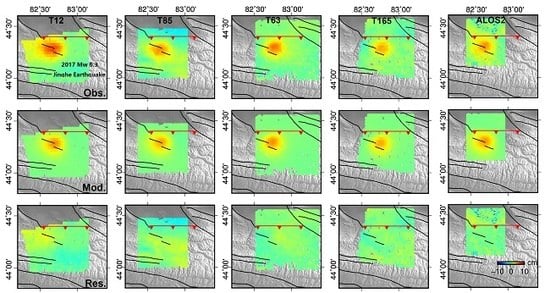
3.4. Displacement Fields Analysis and Evaluation
4. Fault Parameters and Slip Distribution Inversion
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- CENC. 2017/08/09 Jinghe, Xinjiang Province M6.6 Earthquake. Available online: https://www.cenc.ac.cn/cenc/_300651/335684/index.html (accessed on 1 February 2019).
- USGS. M 6.3—109km SSE of Dostyq, Kazakhstan. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us2000a65e/executive (accessed on 1 February 2019).
- Ekström, G.; Nettles, M.; Dziewonski, A. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200, 1–9. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Chou, T.-A.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. Space Phys. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Jiang, X.; Han, Y.; Yang, W.; Meng, L. Preliminary analysis of the 2017 Jinghe Ms 6.6 earthquake sequence and its seismic source characteristics. Earthq. Res. China 2017, 33, 682–693. [Google Scholar]
- Ghose, S.; Hamburger, M.W.; Ammon, C.J. Source parameters of moderate-sized earthquakes in the Tien Shan, central Asia from regional moment tensor inversion. Geophys. Res. Lett. 1998, 25, 3181–3184. [Google Scholar] [CrossRef]
- Avouac, J.P.; Tapponnier, P.; Bai, M.; You, H.; Wang, G. Active thrusting and folding along the northern Tien Shan and Late Cenozoic rotation of the Tarim relative to Dzungaria and Kazakhstan. J. Geophys. Res. Space Phys. 1993, 98, 6755–6804. [Google Scholar] [CrossRef] [Green Version]
- Deng, Q.; Feng, X.; Yang, X. Study on Holocene paleoearthquake by large trench in the Manas-Tugulu reverse faultand-fold zone along Northern margin of the Tian Shan mountain in Xinjiang. In Research on Active Faults Series; Seismological Press: Beijing, China, 1994; Volume 3. (In Chinese) [Google Scholar]
- Qiao, X.; Wang, Q.; Yang, S. Study on the focal mechanism and deformation characteristics for the 2008 Mw6.7 Wuqia earthquake, Xinjiang by InSAR. Chin. J. Geophys. 2013, 57, 1805–1813. (In Chinese) [Google Scholar]
- Wang, X.; Xu, C.; Wen, Y.; Wang, S.; Xu, G.; Xiao, Z.; Fang, L. The 2016 Mw 6.0 Hutubi earthquake: A blind thrust event along the northern Tian Shan front. J. Asian Earth Sci. 2019, 173, 79–87. [Google Scholar] [CrossRef]
- Bai, L.; Liu, J.; Zhang, Y.; Wu, Q.; An, Y. Relocation of the 2017 Ms 6.6 Jinghe, Xinjiang earthquake sequence and its seismogenic structure. Earthq. Res. China 2017, 33, 703–711. [Google Scholar]
- Liu, J.; Gao, R.; Wang, Q.; Nie, X. Relocation of the Jinghe Ms 6.6 earthquake sequence on August 9, 2017 and analysis of the seismogenic structure. Earthq. Res. China 2017, 33, 663–670. (In Chinese) [Google Scholar]
- Liu, C.; Qiu, J.; Wang, J. The 2017 Jinghe Ms 6.6 Earthquake Inversion from Ascending and Descending Sentinel-1 Observations. J. Geod. Geodyn. 2018, 38, 1111–1116. [Google Scholar]
- Kreemer, C.; Blewitt, G.; Klein, E.C. A geodetic plate motion and Global Strain Rate Model. Geochem. Geophys. Geosyst. 2014, 15, 3849–3889. [Google Scholar] [CrossRef]
- Burchfiel, B.C.; Brown, E.T.; Qidong, D.; Xianyue, F.; Jun, L.; Molnar, P.; Jianbang, S.; Zhangming, W.; Huichuan, Y. Crustal Shortening on the Margins of the Tien Shan, Xinjiang, China. Int. Geol. Rev. 1999, 41, 665–700. [Google Scholar] [CrossRef]
- Yang, S.; Li, J.; Wang, Q. The deformation pattern and fault rate in the Tianshan Mountains inferred from GPS observations. Sci. China Ser. D Earth Sci. 2008, 51, 1064–1080. [Google Scholar] [CrossRef]
- Tapponnier, P.; Molnar, P. Active faulting and cenozoic tectonics of the Tien Shan, Mongolia, and Baykal Regions. J. Geophys. Res. Space Phys. 1979, 84, 3425–3459. [Google Scholar] [CrossRef]
- Weldon, R.J.; Rubin, C.M.; Molnar, P.; Thompson, S.C.; Abdrakhmatov, K.; Berger, G.W. Late Quaternary slip rates across the central Tien Shan, Kyrgyzstan, central Asia. J. Geophys. Res. Space Phys. 2002, 107, 1–32. [Google Scholar]
- Deng, Q.; Feng, X.; Zhang, P.; Xu, X.; Yang, X.; Peng, S.; Li, J. Active Tectonic of Tian Shan, 1st ed.; Seismological Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Chen, J.; Shen, J.; Li, J.; Yang, J.; Hu, W.; Zhao, X.; Zeng, X. Preliminary study on new active characteristics of Kusongmuxieke mountain front fault in the west segment of north Tianshan. Northwest. Seismol. J. 2007, 29, 335–340. (In Chinese) [Google Scholar]
- Chen, J.; Tan, M.; Wu, G.; Hu, W.; Sun, J.; Zhang, Z. The Seismic Damage Characteristic and the Cause of the Jinhe M5.0 Earthquake in Xinjiang on Oct. 16, 2011. Technol. Earthq. Disaster Prev. 2012, 7, 164–172. (In Chinese) [Google Scholar]
- USGS. M 5.2—112km ENE of Yining Xian, China. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us1000hcmu/moment-tensor (accessed on 1 February 2019).
- Liu, P.; Han, G.; Nie, X. M5.4 Earthquake on October 16, 2018 in Jinghe Xinjiang; Earthquake Administration of Xinjiang, CEA: Beijing, China, 2018. [Google Scholar]
- ASF. Sentinel-1. Available online: https://www.asf.alaska.edu/sentinel/ (accessed on 1 February 2019).
- Parsons, B.; Wright, T.; Fielding, E. Measurement of interseismic strain accumulation across the North Anatolian Fault by satellite radar interferometry. Geophys. Res. Lett. 2001, 28, 2117–2120. [Google Scholar]
- JAXA. ALOS-2 Basic Observation Scenario, 1st ed.; JAXA: Tokyo, Japan, 2014. Available online: http://www.eorc.jaxa.jp/ALOS-2/en/obs/scenario/ALOS-2_Basic_Observation_Scenario_First-Ed_E_v00.pdf (accessed on 1 February 2019).
- Hanssen, R. Radar Interferometry: Data Interpretation and Error Analysis, 1 ed.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2001; Volume 2. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Space Phys. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Gonzalez, P.J.; Tiampo, K.F.; Camacho, A.G.; Fernández, J. Shallow flank deformation at Cumbre Vieja volcano (Canary Islands): Implications on the stability of steep-sided volcano flanks at oceanic islands. Earth Planet. Sci. Lett. 2010, 297, 545–557. [Google Scholar] [CrossRef]
- Jiang, L.; Li, C.; Qiu, G.; Wang, H.; Wright, T.J.; Yu, Y.; Lin, H. InSAR reveals coastal subsidence in the Pearl River Delta, China. Geophys. J. Int. 2012, 191, 1119–1128. [Google Scholar] [Green Version]
- Dong, J.; Zhang, L.; Liao, M.; Gong, J. Improved Correction of Seasonal Tropospheric Delay in InSAR Observations for Landslide Deformation Monitoring. Remote Sens. Environ. 2019. under review. [Google Scholar] [CrossRef]
- Bie, L.; Ryder, I.; Nippress, S.E.; Bürgmann, R. Coseismic and post-seismic activity associated with the 2008 Mw 6.3 Damxung earthquake, Tibet, constrained by InSAR. Geophys. J. Int. 2013, 196, 788–803. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Werner, C.L.; Wegmüller, U.; Strozzi, T. Processing Strategies for Phase Unwrapping for InSAR Applications. In Proceedings of the EUSAR 2002—4th European Conference on Synthetic Aperture Radar, Cologne, Germany, 4–6 June 2002; pp. 353–356. [Google Scholar]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Doin, M.P.; Guillaso, S.; Jolivet, R.; Lasserre, C.; Lodge, F.; Ducret, G.; Gradin, R. Presentation of the small baseline NSBAS processing chain on a case example: The Etna deformation monitoring from 2003 to 2010 using Envisat data. In Proceedings of the ESA FRINGE 2011 Conference, Frascati, Italy, 19–23 September 2011. [Google Scholar]
- Gray, A.L.; Mattar, K.E. Influence of Ionospheric Electron Density Fluctuations on Satellite Radar Interferometry. Geophys. Res. Lett. 2000, 27, 1451–1454. [Google Scholar] [CrossRef]
- Meyer, F. A review of ionospheric effects in low-frequency SAR—Signals, correction methods, and performance requirements. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 29–32. [Google Scholar]
- King, G.C.P.; Stein, R.S.; Rundle, J.B. The Growth of Geological Structures by Repeated Earthquakes 1. Conceptual Framework. J. Geophys. Res. Space Phys. 1988, 93, 13307–13318. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.; Zhang, Y.; Shan, X. Source parameters of the 2016 Menyuan earthquake in the northeastern Tibetan Plateau determined from regional seismic waveforms and InSAR measurements. J. Asian Earth Sci. 2018, 158, 103–111. [Google Scholar] [CrossRef]
- Parsons, B.E.; Lu, Z.; Wright, T.J. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Diao, F.; Hoechner, A. SDM—A geodetic inversion code incorporating with layered crust structure and curved fault geometry. In Proceedings of the General Assembly European Geosciences Union, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Jonsson, S. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements. Bull. Seism. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
- Okada, Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Lohman, R.; Barnhart, W.D. Evaluation of earthquake triggering during the 2005–2008 earthquake sequence on Qeshm Island, Iran. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Lohman, R.B.; Simons, M.; Savage, B. Location and mechanism of the Little Skull Mountain earthquake as constrained by satellite radar interferometry and seismic waveform modeling. J. Geophys. Res. Space Phys. 2002, 107, 7–10. [Google Scholar] [CrossRef]
- Mencin, D.; Bendick, R.; Upreti, B.N.; Adhikari, D.P.; Gajurel, A.P.; Bhattarai, R.R.; Shrestha, H.R.; Bhattarai, T.N.; Manandhar, N.; Galetzka, J.; et al. Himalayan strain reservoir inferred from limited afterslip following the Gorkha earthquake. Nat. Geosci. 2016, 9, 533–537. [Google Scholar] [CrossRef]
- Wimpenny, S.; Copley, A.; Ingleby, T. Fault mechanics and post-seismic deformation at Bam, SE Iran. Geophys. J. Int. 2017, 209, 1018–1035. [Google Scholar] [CrossRef] [Green Version]










| Source a | Lat. (°) | Lon. (°) | Depth (km) | Nodal Plane 1 (°) | Nodal Plane 2 (°) | Mw | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Strike | Dip | Rake | Strike | Dip | Rake | |||||
| USGS | 82,827 | 44,301 | 20 | 269 | 30 | 87 | 92 | 60 | 92 | 6.3 |
| GCMT | 82,740 | 44,400 | 27.6 | 244 | 52 | 66 | 101 | 44 | 118 | 6.3 |
| CENC | 82,890 | 44,270 | 11.0 | 269 | 47 | 99 | 76 | 44 | 80 | 6.3 |
| Satellite | Track-Orbit 2 | Single Pair Min. SD (cm) | Single Pair Max. SD (cm) | Averaged Disp. SD. (cm) | Heading (Deg.) | Average Inc. (Deg.) | Max. LoS Disp. (cm) |
|---|---|---|---|---|---|---|---|
| S1 | T12A | 1.95 | 3.87 | 1.14 | −10.76 | 33.53 | 6.46 |
| S1 | T85A | 1.86 | 3.35 | 1.27 | −9.32 | 43.3 | 4.88 |
| S1 | T63D | 1.71 | 2.88 | 0.74 | −169.44 | 35 | 5.56 |
| S1 | T165D | 1.48 | 2.32 | 0.81 | −170.83 | 44.26 | 4.51 |
| ALOS2 3 | 880A | 2.44 | 2.97 | 2.44 | −10.89 | 38.7 | 6.42 |
| Model | Lon./° | Lat./° | Z/km | Strike | Dip | Rake | Mw |
|---|---|---|---|---|---|---|---|
| InSAR-ND | 82.74 | 44.29 | 16.73 | 270 | 42 | 84.02 | 6.37 |
| InSAR-SD | 82.72 | 44.26 | 14.05 | 90 | 42 | 89.56 | 6.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, W.; Zhang, Y.; Li, T.; Wen, S.; Zhao, D.; Hou, L.; Shan, X. Multi-Sensor Geodetic Observations and Modeling of the 2017 Mw 6.3 Jinghe Earthquake. Remote Sens. 2019, 11, 2157. https://doi.org/10.3390/rs11182157
Gong W, Zhang Y, Li T, Wen S, Zhao D, Hou L, Shan X. Multi-Sensor Geodetic Observations and Modeling of the 2017 Mw 6.3 Jinghe Earthquake. Remote Sensing. 2019; 11(18):2157. https://doi.org/10.3390/rs11182157
Chicago/Turabian StyleGong, Wenyu, Yingfeng Zhang, Tao Li, Shaoyan Wen, Dezheng Zhao, Liyan Hou, and Xinjian Shan. 2019. "Multi-Sensor Geodetic Observations and Modeling of the 2017 Mw 6.3 Jinghe Earthquake" Remote Sensing 11, no. 18: 2157. https://doi.org/10.3390/rs11182157
APA StyleGong, W., Zhang, Y., Li, T., Wen, S., Zhao, D., Hou, L., & Shan, X. (2019). Multi-Sensor Geodetic Observations and Modeling of the 2017 Mw 6.3 Jinghe Earthquake. Remote Sensing, 11(18), 2157. https://doi.org/10.3390/rs11182157