Structural 3D Reconstruction of Indoor Space for 5G Signal Simulation with Mobile Laser Scanning Point Clouds
Abstract
:1. Introduction
2. Related Work
2.1. Room Segmentation
2.2. Reconstruction of Indoor Space
(1) Surface-Based Reconstruction
(2) Line-Based Reconstruction
2.3. Indoor Model Application
2.4. Summary
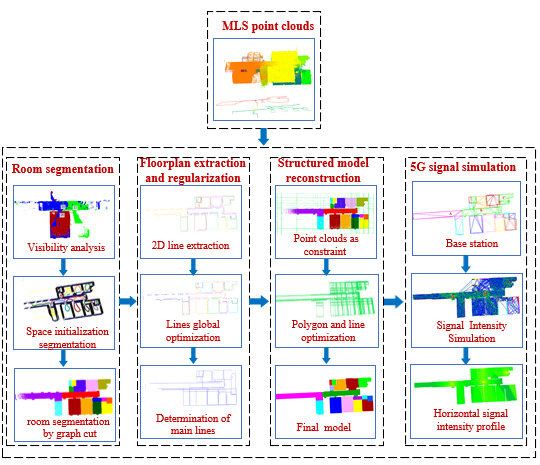
3. Methodology
3.1. Room Segmentation
3.1.1. Detection of Openings
3.1.2. Room-Space Segmentation
3.2. Floorplan Extraction and Regularization
3.2.1. Floorplan Line Extraction
3.2.2. Line Global Optimization
3.2.3. Clustering Similar Lines
3.3. Structured Model Reconstruction
3.3.1. Model Reconstruction
3.3.2. Room Structured Connection
3.3.3. G Signal Intensity Simulation
4. Experiment
4.1. Datasets
4.2. Parameters
4.3. Results
5. Evaluation and Discussion
5.1. Quantitative Evaluation
5.2. Limitations
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Becker, S.; Peter, M.; Fritsch, D. Grammar-Supported 3d Indoor Reconstruction from Point Clouds for As-Built Bim. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 17–24. [Google Scholar] [CrossRef]
- Vilariño, L.D.; Boguslawski, P.; Khoshelham, K.; Lorenzo, H.; Mahdjoubi, L. Indoor Navigation from Point Clouds: 3d Modelling and Obstacle Detection. ISPRS Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B4, 275–281. [Google Scholar]
- Vilariño, L.D.; Frias, E.; Balado, J.; Gonzalezjorge, H. Scan planning and route optimization for control of execution of as-designed BIM. ISPRS Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, XLII-4, 143–148. [Google Scholar]
- Boyes, G.; Ellul, C.; Irwin, D. Exploring bim for operational integrated asset management-a preliminary study utilising real-world infrastructure data. ISPRS Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2017, IV-4/W5, 49–56. [Google Scholar] [CrossRef]
- Tomasi, R.; Sottile, F.; Pastrone, C.; Mozumdar, M.M.R.; Osello, A.; Lavagno, L. Leveraging bim interoperability for uwb-based wsn planning. IEEE Sens. J. 2015, 15, 5988–5996. [Google Scholar] [CrossRef]
- Rafiee, A.; Dias, E.; Fruijtier, S.; Rafiee, A.; Dias, E.; Fruijtier, S.; Scholten, H. From bim to geo-analysis: View coverage and shadow analysis by bim/gis integration. Procedia Environ. Sci. 2014, 22, 397–402. [Google Scholar] [CrossRef]
- Tang, D.; Kim, J. Simulation support for sustainable design of buildings. In Proceedings of the CTBUH International Conference, Shanghai, China, 16–19 September 2014. [Google Scholar]
- Boguslawski, P.; Mahdjoubi, L.; Zverovich, V.E.; Fadli, F. Two-graph building interior representation for emergency response applications. ISPRS Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, III-2, 9–14. [Google Scholar]
- Bassier, M.; Vergauwen, M. Clustering of Wall Geometry from Unstructured Point Clouds Using Conditional Random Fields. Remote Sens. 2019, 11, 1586. [Google Scholar] [CrossRef]
- Ikehata, S.; Yang, H.; Furukawa, Y. Structured Indoor Modeling. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Wang, J.; Xu, K.; Liu, L.; Cao, J.; Liu, S.; Yu, Z.; Gu, X. Consolidation of low-quality point clouds from outdoor scenes. Comput. Graph. Forum. 2013, 32, 207–216. [Google Scholar] [CrossRef]
- Mura, C.; Mattausch, O.; Villanueva, A.J.; Gobbetti, E.; Pajarola, R. Automatic room detection and reconstruction in cluttered indoor environments with complex room layouts. Comput. Graph. 2014, 44, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Ochmann, S.; Vock, R.; Wessel, R.; Tamke, M.; Klein, R. Automatic generation of structural building descriptions from 3D point cloud scans. In Proceedings of the International Conference on Computer Graphics Theory and Applications, Lisbon, Portugal, 5–8 January 2014. [Google Scholar]
- Turner, E.; Cheng, P.; Zakhor, A. Fast, Automated, Scalable Generation of Textured 3D Models of Indoor Environments. IEEE J. Sel. Top. Signal. Process. 2015, 9, 409–421. [Google Scholar] [CrossRef]
- Ochmann, S.; Vock, R.; Wessel, R.; Klein, R. Automatic reconstruction of parametric building models from indoor point clouds. Comput. Graph. 2016, 54, 94–103. [Google Scholar] [CrossRef] [Green Version]
- Ambrus, R.; Claici, S.; Wendt, A. Automatic Room Segmentation from Unstructured 3-D Data of Indoor Environments. In Proceedings of the International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017. [Google Scholar]
- Wang, R.; Xie, L.; Chen, D. Modeling Indoor Spaces Using Decomposition and Reconstruction of Structural Elements. Photogramm. Eng. Remote Sens. 2017, 83, 827–841. [Google Scholar] [CrossRef]
- Vilariño, L.D.; Verbree, E.; Zlatanova, S.; Diakité, A. Indoor Modelling from Slam-Based Laser Scanner: Door Detection to Envelope Reconstruction. ISPRS Int. Arch. Photogramm. Remote Sens. 2017, XLII-2/W7, 345–352. [Google Scholar]
- Li, L.; Su, F.; Yang, F.; Zhu, H.; Li, D.; Zuo, X.; Li, F.; Liu, Y.; Ying, S. Reconstruction of Three—Dimensional (3D) Indoor Interiors with Multiple Floors via Comprehensive Segmentation. Remote Sens. 2018, 10, 1281. [Google Scholar] [CrossRef]
- Yang, F.; Li, L.; Su, F.; Li, D.L.; Zhu, H.H.; Ying, S.; Zuo, X.K.; Tang, L. Semantic decomposition and recognition of indoor spaces with structural constraints for 3D indoor modelling. Automat. Constrn. 2019, 106, 102913. [Google Scholar] [CrossRef]
- Stichting, C.; Centrum, M.; Dongen, S.V. A Cluster Algorithm for Graphs; CWI: Amsterdam, The Netherlands, 2000; pp. 1–40. [Google Scholar]
- Ochmann, S.; Vock, R.; Klein, R. Automatic reconstruction of fully volumetric 3D building models from oriented point clouds. ISPRS J. Photogramm. Remote Sens. 2019, 151, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, V.; Zakhor, A. Planar 3D modeling of building interiors from point cloud data. In Proceedings of the IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012. [Google Scholar]
- Lafarge, F.; Alliez, P. Surface Reconstruction through Point Set Structuring. Comput. Graph. Forum. 2013, 32, 225–234. [Google Scholar] [CrossRef] [Green Version]
- Monszpart, A.; Mellado, N.; Brostow, G.; Mitra, N. RAPter: Rebuilding man-made scenes with regular arrangements of planes. Acm Trans. Graph. 2015, 34, 103. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Gilani, S.A.; Siddiqui, F.U. An Effective Data-Driven Method for 3-D Building Roof Reconstruction and Robust Change Detection. Remote Sens. 2018, 10, 1512. [Google Scholar] [CrossRef]
- Xiao, J.; Furukawa, Y. Reconstructing the world’s museums. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Mura, C.; Mattausch, O.; Pajarola, R. Piecewise-planar Reconstruction of Multi-room Interiors with Arbitrary Wall Arrangements. Comput. Graph. Forum 2016, 35, 179–188. [Google Scholar] [CrossRef]
- Boulch, A.; Gorce, M.D.L.; Marlet, R. Piecewise-Planar 3D Reconstruction with Edge and Corner Regularization. Comput. Graph. Forum. 2014, 33, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Li, Q.; Yang, B.; Xiao, W.; Chen, C.; Dong, Z. Automatic 3-D Reconstruction of Indoor Environment with Mobile Laser Scanning Point Clouds. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 99, 1–14. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Chen, B.L.; Zai, D.W.; Li, J. Facet Segmentation-Based Line Segment Extraction for Large-Scale Point Clouds. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4839–4854. [Google Scholar] [CrossRef]
- Xia, S.; Wang, R. Façade Separation in Ground-Based LiDAR Point Clouds Based on Edges and Windows. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 1041–1052. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Y.; Li, K. Fast 3D Line Segment Detection from Unorganized Point Cloud. In Proceedings of the IEEE Conference on Computer Vision Pattern Recognition, Long Beach UA, CA, USA, 15–21 June 2019. [Google Scholar]
- Liu, C.; Wu, J.; Furukawa, Y. FloorNet: A Unified Framework for Floorplan Reconstruction from 3D Scans. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Oesau, S.; Lafarge, F.; Alliez, P. Indoor scene reconstruction using feature sensitive primitive extraction and graph-cut. ISPRS J. Photogramm. Remote Sens. 2014, 90, 68–82. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Hou, S.; Wen, C.; Gong, Z.; Li, Q.; Sun, X.; Li, J. Semantic line framework-based indoor building modeling using backpacked laser scanning point cloud. ISPRS J. Photogramm. Remote Sens. 2018, 143, 150–166. [Google Scholar] [CrossRef]
- Bauchet, J.; Lafarge, F. KIPPI: KInetic Polygonal Partitioning of Images. In Proceedings of the IEEE Conference on Computer Vision Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Sui, W.; Wang, L.; Fan, B.; Xiao, H.; Wu, H.; Pan, C. Layer-Wise Floorplan Extraction for Automatic Urban Building Reconstruction. IEEE Trans. Vis. Comput. Graph. 2016, 22, 1261–1277. [Google Scholar] [CrossRef]
- Novakovic, G.; Lazar, A.; Kovacic, S.; Vulic, M. The Usability of Terrestrial 3D Laser Scanning Technology for Tunnel Clearance Analysis Application. Appl. Mech. Mater. 2014, 683, 219–224. [Google Scholar] [CrossRef]
- Suzuki, S.; Be, K. Topological structural analysis of digitized binary images by border following. Comput. Vis. Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- OpenCV. Available online: https://opencv.org/ (accessed on 2 April 2019).
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef] [PubMed]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Kolmogorov, V.; Zabin, R. What energy functions can be minimized via graphcuts? IEEE Trans. Pattern Anal. Mach. Intell. 2002, 26, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Von Gioi, R.G.V.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A Fast Line Segment Detector with a False Detection Control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G 2 o: A general framework for graph Optimization. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Yang, G.; Chen, J. Research on Propagation Model for 5G Mobile Communication Systems. Mob. Commun. 2018, 42, 28–33. [Google Scholar]
- 5G. Study on Channel Model for Frequencies from 0.5 to 100 GHZ (3GPP TR 38.901 version 14.0.0 release 14). Available online: http://www.etsi.org/standards-search (accessed on 5 May 2017).
- Khoshelham, K.; Vilariño, L.D.; Peter, M.; Kang, Z.; Acharya, D. The ISPRS benchmark on indoor modelling. Int. Arch. Photogramme. Remote Sens. Spat. Inf. Sci. 2017, XLII-2/W7, 367–372. [Google Scholar] [CrossRef]
- Chew, L.P. Constrained Delaunay triangulations. Algorithmica 1989, 4, 97–108. [Google Scholar] [CrossRef]























| Sensor | ZEB REVO | BLS (Shenzhen University) | BLS (Xiamen University) |
|---|---|---|---|
| Max range | 30 m | 100 m | 100 m |
| Speed (points/sec) | 43 × 103 | 300 × 103 | 300 × 103 |
| Horizontal Angular Resolution | 0.625° | 0.1–0.4° | 0.1–0.4° |
| Vertical Angular Resolution | 1.8° | 2.0° | 2.0° |
| Angular FOV | 270 × 360° | 30 × 360° | 2 × 30 × 360° |
| Dataset | Benchmark Data | Corridor (Shenzhen University) | Corridor (Xiamen University) | Parking lot (Xiamen University) |
|---|---|---|---|---|
| Number of points | 21.560.263 | 1.980.911 | 2.098.634 | 7.683.766 |
| Clutter | Low | High | Low | High |
| Parameters | Values | Descriptions |
|---|---|---|
| Extracting Openings | ||
| The size of the pixel (point clouds transform into image) | ||
| The width and height of regularized door | ||
| The width and height of the regularized window | ||
| Segmentation of Rooms | ||
| The size of the 3D grid (point clouds transform into 3D grid) | ||
| Parameters of data term and smooth term of the energy function | ||
| Line Global Optimization | ||
| Angle correction of lines | ||
| Distance correction of lines | ||
| k-nearest of lines | ||
| The weight parameter of line global optimization | ||
| Cluster Similar Lines | ||
| Angle threshold of merging similar lines | ||
| Distance threshold of merging similar lines | ||
| 5G Signal Intensity Simulation | ||
| The signal propagation distance | ||
| The frequency of the electromagnetic wave | ||
| The power exponent by IDW interpolation | ||
| Description | Number of Points | Actual/Detected Doors | Actual/Detected Windows | Actual/Detected Rooms | Actual/Detected Pillars |
|---|---|---|---|---|---|
| Benchmark data | 11,628,186 | 51/42 | 21/8 | 25/25 | 0/0 |
| Corridor (Shenzhen University) | 1,980,911 | 4/4 | 0/0 | 1/1 | 6/6 |
| Corridor (Xiamen University) | 7,683,766 | 8/8 | 11/11 | 1/1 | 0/0 |
| Parking Lot (Xiamen University) | 2,098,634 | 0/0 | 0/0 | 1/1 | 23/18 |
| Description | Surface Extraction (s) | Opening Detection (s) | Room Segmentation (s) | Line Regularization and Model Reconstruction (s) | Total Time (s) |
|---|---|---|---|---|---|
| Benchmark data | 80 | 19 | 287 | 49 | 435 |
| Corridor (Shenzhen University) | 9 | 4 | 0 | 24 | 37 |
| Corridor (Xiamen University) | 7 | 6 | 0 | 20 | 33 |
| Parking Lot (Xiamen University) | 28 | 0 | 0 | 32 | 60 |
| Error/m | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 |
| Benchmark first floor (%) | 51.50 | 27.68 | 12.92 | 3.26 | 1.73 | 1.61 | 0.28 | 0.21 | 0.20 | 0.11 | 0.10 | 0.09 | 0.07 | 0.07 | 0.08 | 0.05 | 0.02 | 0.01 | 0.01 |
| Benchmark second floor (%) | 52.31 | 30.09 | 9.36 | 3.20 | 2.41 | 2.11 | 0.31 | 0.07 | 0.01 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| Corridor, Shenzhen University (%) | 25.10 | 25.81 | 22.02 | 7.45 | 5.51 | 3.81 | 3.02 | 2.55 | 1.10 | 0.81 | 0.82 | 0.40 | 0.51 | 0.50 | 0.14 | 0.12 | 0.21 | 0.01 | 0.11 |
| Corridor, Xiamen University (%) | 75.83 | 15.49 | 4.81 | 1.75 | 0.62 | 0.60 | 0.11 | 0.11 | 0.41 | 0.10 | 0.02 | 0.01 | 0.02 | 0.05 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 |
| Parking lot, Xiamen University (%) | 32.82 | 20.87 | 15.71 | 10.92 | 5.38 | 3.30 | 2.62 | 2.01 | 1.37 | 1.23 | 1.06 | 0.91 | 0.44 | 0.26 | 0.27 | 0.23 | 0.20 | 0.25 | 0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Li, Q.; Dong, Z. Structural 3D Reconstruction of Indoor Space for 5G Signal Simulation with Mobile Laser Scanning Point Clouds. Remote Sens. 2019, 11, 2262. https://doi.org/10.3390/rs11192262
Cui Y, Li Q, Dong Z. Structural 3D Reconstruction of Indoor Space for 5G Signal Simulation with Mobile Laser Scanning Point Clouds. Remote Sensing. 2019; 11(19):2262. https://doi.org/10.3390/rs11192262
Chicago/Turabian StyleCui, Yang, Qingquan Li, and Zhen Dong. 2019. "Structural 3D Reconstruction of Indoor Space for 5G Signal Simulation with Mobile Laser Scanning Point Clouds" Remote Sensing 11, no. 19: 2262. https://doi.org/10.3390/rs11192262
APA StyleCui, Y., Li, Q., & Dong, Z. (2019). Structural 3D Reconstruction of Indoor Space for 5G Signal Simulation with Mobile Laser Scanning Point Clouds. Remote Sensing, 11(19), 2262. https://doi.org/10.3390/rs11192262