Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multi-GNSS Positioning Models
2.1.1. Single-Frequency SPP
2.1.2. Single-Frequency PPP
2.1.3. Dual-Frequency PPP
2.2. Ionospheric Correction Models
2.2.1. BIM
2.2.2. NTCM
2.2.3. GIM
3. Data and Processing Strategy
4. Results and Discussion
4.1. Performance of Single-Frequency SPP
4.2. Performance of Single-Frequency PPP
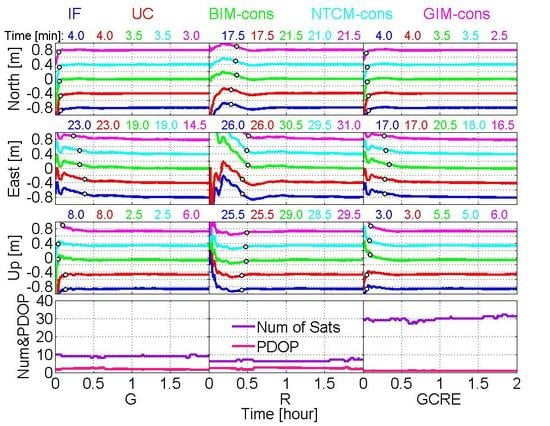
4.3. Performance of Dual-Frequency PPP
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jin, S.G.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Chen, L.; Yi, W.; Song, W.; Shi, C.; Lou, Y.; Cao, C. Evaluation of three ionospheric delay computation methods for ground-based GNSS receivers. GPS Solut. 2018, 22, 125. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Radicella, S.M. The NeQuick model genesis, uses and evolution. Ann. Geophys. 2009, 52, 417–422. [Google Scholar]
- Jakowski, N.; Hoque, M.M.; Mayer, C. A new global TEC model for estimating transionospheric radio wave propagation errors. J. Geod. 2011, 85, 965–974. [Google Scholar] [CrossRef]
- Odijk, D. Ionosphere-free phase combinations for modernized GPS. J. Surv. Eng. 2003, 129, 165–173. [Google Scholar] [CrossRef]
- Pengfei, C.; Wei, L.; Jinzhong, B.; Hanjiang, W.; Yanhui, C.; Hua, W. Performance of precise point positioning (PPP) based on uncombined dual-frequency GPS observables. Survey Rev. 2011, 43, 343–350. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Gu, S.; Shi, C.; Lou, Y.; Liu, J. Ionospheric effects in uncalibrated phase delay estimation and ambiguity-fixed PPP based on raw observable model. J. Geod. 2015, 89, 447–457. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Ge, M.; Niu, X.; Huang, L.; Tu, R.; Li, X. On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors 2013, 13, 15708–15725. [Google Scholar] [CrossRef]
- Cai, C.; Liu, Z.; Luo, X. Single-frequency ionosphere-free precise point positioning using combined GPS and GLONASS observations. J. Navig. 2013, 66, 417–434. [Google Scholar] [CrossRef]
- Cai, C.; Gong, Y.; Gao, Y.; Kuang, C. An Approach to Speed up Single-Frequency PPP Convergence with Quad-Constellation GNSS and GIM. Sensors 2017, 17, 1302. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Schönemann, E.S.; Becker, M.; Springer, T. A new approach for GNSS analysis in a multi-GNSS and multi-signal environment. J. Geod. Sci. 2011, 1, 204–214. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Huo, X. Improvement of Klobuchar model for GNSS single-frequency ionospheric delay corrections. Adv. Space Res. 2016, 57, 1555–1569. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document—Open Service Signal B3I. Version 1.0; China Satellite Navigation Office: Beijing, China, 2018. [Google Scholar]
- Nava, B.; Coisson, P.; Radicella, S.M. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol. Terrest. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N.; Berdermann, J. Ionospheric Correction using NTCM driven by GPS Klobuchar coefficients for GNSS applications. GPS Solut. 2017, 21, 1563–1572. [Google Scholar] [CrossRef]
- Otsuka, Y.; Ogawa, T.; Saito, A.; Tsugawa, T.; Fukao, S.; Miyazaki, S. A new technique for mapping of total electron content using GPS network in Japan. Earth Planets Space 2002, 54, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Schaer, S.; Gartner, W.; Feltens, J. IONEX: The IONosphere Map Exchange Format Version 1. In Proceedings of the IGS AC Workshop, Darmstadt, Germany, 9–11 February 1998. [Google Scholar]
- Witchayangkoon, B. Elements of GPS Precise Point Positioning. Ph.D. Dissertation, Department of Spatial Information Science and Engineering, University of Maine, Orono, ME, USA, 2000. [Google Scholar]
- Gao, Z.; Ge, M.; Shen, W.; Zhang, H.; Niu, X. Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements. J. Geod. 2017, 91, 1351–1366. [Google Scholar] [CrossRef]
- Kalman, R. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Improvement of Multi-GNSS Precise Point Positioning Performances with Real Meteorological Data. J. Navig. 2018, 71, 1363–1380. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products; IGS Central Bureau, Jet Propulsion Laboratory: Pasadena, CA, USA, 2009; p. 34. [Google Scholar]
- Gérard, P.; Luzum, B. IERS Conventions; No. IERS-TN-36; Bureau International des Poids et Mesures: Sevres, France, 2010. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Astrodynamics 1992, 18, 1647–1660. [Google Scholar]
- Schaffrin, B.; Grafarend, E. Generating classes of equivalent linear models by nuisance parameter. Manuscr. Geod. 1986, 11, 262–271. [Google Scholar]
- Xu, G.; Xu, Y. GPS: Theory, Algorithms and Applications, 3nd ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Jin, S.G.; Jin, R.; Li, D. Assessment of BeiDou differential code bias variations from multi-GNSS network observations. Ann. Geophys. 2016, 34, 259–269. [Google Scholar] [CrossRef] [Green Version]









| Items | Strategies |
|---|---|
| Data span | 1–30 September 2018 |
| Signal Selection | GPS: L1/L2/L5; BDS: B1/B2/B3; GLONASS: G1/G2; Galileo: E1/E5a/E5b |
| Estimator | SPP: LS PPP: Kalman filter [23] |
| Observation sampling rate | 30 s |
| Elevation cutoff | 7° |
| Satellite orbit and clock | SPP: broadcast ephemeris provided by MGEX PPP: Fixed by MGEX orbit and clock products |
| Satellite TGD | Correct using broadcast ephemeris for SPP |
| Satellite DCB | Correct using MGEX DCB products for PPP |
| Tropospheric delay | SPP: Modified Hopfield PPP: Modified Hopfield for dry part and estimated for wet part as random-walk process (10−9 m2/s) [24] |
| Ionospheric delay | Eliminated or estimated as white noise Strategies in Table 2 |
| Relativistic effect | General relativistic models [25] |
| Sagnac effect | Corrected model [26] |
| Phase windup effect | Corrected model [27] |
| Satellite and receiver antenna | Corrected with the values from MGEX and IGS [26] |
| Tide displacement | Corrected, including solid Earth, pole and ocean tide [26] |
| Station reference coordinates | IGS SINEX solutions |
| Station coordinate | Estimated as constants |
| Receiver clock | Estimated as white noise process (1×105 m2) |
| Receiver IFB | Estimated as constants or absorbed by receiver clock biases |
| Phase ambiguities | Estimated as constants for float values |
| Constellation | Mode | Schemes | Comment |
|---|---|---|---|
| G, C, R, E | Single-frequency SPP: b1, b2, b3 | BIM-corr; NTCM-corr; GIM-corr; | In the BIM, different ionospheric delay models are utilized for their corresponding systems. Klobuchar model (G/R); improved Klobuchar model(C); NeQuick model(E) |
| G/C | |||
| G/R | Single-frequency PPP: b1, b2, b3 | GRAPHIC; UC; BIM-cons; NTCM-cons; GIM-cons; | |
| G/E | |||
| G/C/R | Dual-frequency PPP: b1-b2;b1-b3 | IF; UC; BIM-cons; NTCM-cons; GIM-cons; | |
| G/C/R/E |
| Type | Schemes | b1 | b2 | b3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | ||
| G | BIM | 2.084 | 1.680 | 4.092 | 2.491 | 1.806 | 5.338 | - | - | - |
| G | NTCM | 2.152 | 1.634 | 3.673 | 2.634 | 1.750 | 4.135 | - | - | - |
| G | GIM | 1.704 | 1.570 | 3.589 | 1.768 | 1.574 | 3.649 | - | - | - |
| C | BIM | 4.455 | 6.516 | 8.195 | 4.685 | 6.166 | 8.226 | 4.096 | 6.203 | 7.364 |
| C | NTCM | 4.348 | 6.112 | 7.621 | 4.683 | 5.819 | 7.423 | 4.219 | 5.810 | 7.055 |
| C | GIM | 4.052 | 6.093 | 7.717 | 4.037 | 4.801 | 7.475 | 3.681 | 5.721 | 6.990 |
| R | BIM | 2.410 | 2.168 | 5.422 | 2.607 | 2.274 | 6.382 | - | - | - |
| R | NTCM | 2.356 | 2.061 | 5.040 | 2.618 | 2.156 | 5.593 | - | - | - |
| R | GIM | 2.169 | 2.022 | 4.980 | 2.204 | 2.080 | 5.401 | - | - | - |
| E | BIM | 3.117 | 2.802 | 5.149 | 3.466 | 2.935 | 6.332 | 3.506 | 3.033 | 6.112 |
| E | NTCM | 3.190 | 2.769 | 4.754 | 3.804 | 3.026 | 5.598 | 3.767 | 3.041 | 5.443 |
| E | GIM | 2.773 | 2.704 | 4.604 | 2.936 | 2.910 | 5.166 | 3.025 | 3.011 | 2.113 |
| GC | BIM | 2.073 | 1.667 | 4.077 | 2.480 | 1.793 | 5.324 | 2.718 | 3.291 | 6.770 |
| GC | NTCM | 2.141 | 1.625 | 3.660 | 2.624 | 1.739 | 4.122 | 2.823 | 3.103 | 5.857 |
| GC | GIM | 1.690 | 1.559 | 3.578 | 1.758 | 1.562 | 3.636 | 2.136 | 2.997 | 5.413 |
| GR | BIM | 1.749 | 1.396 | 3.419 | 2.067 | 1.495 | 4.428 | - | - | - |
| GR | NTCM | 1.803 | 1.362 | 3.108 | 2.183 | 1.457 | 3.498 | - | - | - |
| GR | GIM | 1.453 | 1.312 | 3.006 | 1.507 | 1.318 | 3.092 | - | - | - |
| GE | BIM | 1.697 | 1.361 | 3.357 | 2.052 | 1.473 | 4.338 | 3.081 | 2.433 | 5.706 |
| GE | NTCM | 1.758 | 1.326 | 2.992 | 2.174 | 1.429 | 3.405 | 2.902 | 2.187 | 5.579 |
| GE | GIM | 1.368 | 1.270 | 2.912 | 1.433 | 1.277 | 2.987 | 2.129 | 1.915 | 4.781 |
| GCR | BIM | 1.748 | 1.394 | 3.414 | 2.066 | 1.493 | 4.425 | - | - | - |
| GCR | NTCM | 1.802 | 1.361 | 3.106 | 2.183 | 1.455 | 3.497 | - | - | - |
| GCR | GIM | 1.451 | 1.310 | 3.005 | 1.506 | 1.317 | 3.091 | - | - | - |
| GCRE | BIM | 1.728 | 1.376 | 3.381 | 2.062 | 1.483 | 4.429 | - | - | - |
| GCRE | NTCM | 1.786 | 1.344 | 3.061 | 2.181 | 1.445 | 3.472 | - | - | - |
| GCRE | GIM | 1.423 | 1.290 | 2.956 | 1.484 | 1.301 | 3.055 | - | - | - |
| GRAPHIC | UC | Ionosphere Constraint | |
|---|---|---|---|
| Observed quantity | m+n+p+q | 2m+2n+2p+2q | 3m+3n+3p+3q |
| Parameter number | m+n+p+q+8 | 2m+2n+2p+2q+8 | 2m+2n+2p+2q+8 |
| Redundancy | −8 | −8 | m+n+p+q−8 |
| Type of the parameters | Position, receiver clock, ZWD, ambiguity | Position, receiver clock, ZWD, slant ionospheric delay, ambiguity | Position, receiver clock, ZWD, slant ionospheric delay, ambiguity |
| Type | Schemes | b1 | b2 | b3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | ||
| G | GRAPHIC | 1.664 | 3.419 | 9.267 | 1.818 | 3.468 | 6.899 | - | - | - |
| G | UC | 1.664 | 3.419 | 9.266 | 1.818 | 3.468 | 6.900 | - | - | - |
| G | BIM-cons | 1.633 | 3.990 | 9.272 | 1.775 | 3.924 | 6.906 | - | - | - |
| G | NTCM-cons | 1.667 | 3.166 | 9.290 | 1.826 | 3.255 | 6.867 | - | - | - |
| G | GIM-cons | 1.642 | 2.895 | 9.286 | 1.824 | 3.196 | 6.825 | - | - | - |
| C | GRAPHIC | 7.844 | 10.153 | 26.782 | 7.223 | 9.826 | 25.374 | 7.037 | 9.877 | 24.515 |
| C | UC | 7.859 | 10.164 | 26.755 | 7.217 | 9.826 | 25.351 | 7.040 | 9.887 | 24.494 |
| C | BIM-cons | 6.318 | 8.635 | 25.645 | 5.672 | 7.271 | 24.606 | 6.540 | 8.036 | 23.508 |
| C | NTCM-cons | 6.989 | 8.045 | 24.288 | 6.065 | 6.700 | 24.302 | 6.799 | 7.801 | 22.575 |
| C | GIM-cons | 6.904 | 7.743 | 22.011 | 5.962 | 6.469 | 22.314 | 6.644 | 7.658 | 21.717 |
| R | GRAPHIC | 4.404 | 8.003 | 20.440 | 4.391 | 8.582 | 17.139 | - | - | - |
| R | UC | 4.403 | 8.003 | 20.503 | 4.384 | 8.559 | 17.142 | - | - | - |
| R | BIM-cons | 4.347 | 8.095 | 19.267 | 4.268 | 8.442 | 16.998 | - | - | - |
| R | NTCM-cons | 4.356 | 8.090 | 18.713 | 4.279 | 8.449 | 16.873 | - | - | - |
| R | GIM-cons | 4.248 | 7.941 | 18.313 | 3.998 | 8.373 | 16.668 | - | - | - |
| E | GRAPHIC | 2.717 | 3.751 | 7.863 | 2.486 | 3.901 | 8.048 | 2.939 | 4.805 | 8.760 |
| E | UC | 2.717 | 3.753 | 7.862 | 2.488 | 3.901 | 8.053 | 2.939 | 4.805 | 8.759 |
| E | BIM-cons | 2.658 | 3.777 | 7.832 | 2.369 | 3.932 | 7.872 | 2.832 | 4.592 | 8.681 |
| E | NTCM-cons | 2.758 | 3.668 | 7.786 | 2.530 | 3.742 | 7.004 | 2.917 | 4.496 | 8.190 |
| E | GIM-cons | 2.521 | 3.532 | 7.750 | 2.315 | 3.236 | 6.906 | 2.666 | 4.424 | 7.906 |
| GC | GRAPHIC | 1.652 | 3.387 | 9.168 | 1.808 | 3.430 | 6.785 | 3.699 | 8.942 | 13.284 |
| GC | UC | 1.652 | 3.387 | 9.165 | 1.808 | 3.429 | 6.787 | 3.699 | 8.941 | 13.282 |
| GC | BIM-cons | 1.628 | 3.908 | 9.242 | 1.746 | 3.907 | 6.839 | 3.304 | 7.860 | 12.912 |
| GC | NTCM-cons | 1.659 | 3.162 | 9.245 | 1.796 | 3.166 | 6.759 | 3.584 | 7.430 | 12.257 |
| GC | GIM-cons | 1.632 | 3.066 | 9.208 | 1.793 | 3.141 | 6.740 | 3.106 | 6.681 | 12.244 |
| GR | GRAPHIC | 1.662 | 3.418 | 9.260 | 1.810 | 3.461 | 6.890 | - | - | - |
| GR | UC | 1.662 | 3.417 | 9.259 | 1.810 | 3.461 | 6.890 | - | - | - |
| GR | BIM-cons | 1.618 | 3.982 | 9.246 | 1.765 | 3.919 | 6.853 | - | - | - |
| GR | NTCM-cons | 1.662 | 3.159 | 9.268 | 1.819 | 3.172 | 6.795 | - | - | - |
| GR | GIM-cons | 1.631 | 2.876 | 9.216 | 1.821 | 3.169 | 6.779 | - | - | - |
| GE | GRAPHIC | 1.568 | 2.905 | 8.657 | 1.606 | 3.123 | 6.879 | 2.903 | 4.489 | 8.089 |
| GE | UC | 1.568 | 2.905 | 8.656 | 1.606 | 3.122 | 6.880 | 2.903 | 4.489 | 8.089 |
| GE | BIM-cons | 1.542 | 3.242 | 8.655 | 1.568 | 3.675 | 6.890 | 2.806 | 4.390 | 8.074 |
| GE | NTCM-cons | 1.585 | 3.007 | 8.634 | 1.620 | 2.899 | 6.832 | 2.864 | 4.164 | 7.837 |
| GE | GIM-cons | 1.543 | 2.480 | 8.620 | 1.618 | 2.861 | 6.819 | 2.829 | 3.235 | 7.715 |
| GCR | GRAPHIC | 1.651 | 3.385 | 9.161 | 1.711 | 3.342 | 6.775 | - | - | - |
| GCR | UC | 1.651 | 3.385 | 9.159 | 1.710 | 3.341 | 6.777 | - | - | - |
| GCR | BIM-cons | 1.550 | 3.098 | 9.013 | 1.664 | 3.840 | 6.762 | - | - | - |
| GCR | NTCM-cons | 1.591 | 2.253 | 8.932 | 1.734 | 3.145 | 6.688 | - | - | - |
| GCR | GIM-cons | 1.550 | 2.047 | 8.844 | 1.699 | 3.129 | 6.597 | - | - | - |
| GCRE | GRAPHIC | 1.557 | 2.885 | 8.579 | 1.599 | 3.095 | 6.670 | - | - | - |
| GCRE | UC | 1.557 | 2.885 | 8.576 | 1.599 | 3.094 | 6.673 | - | - | - |
| GCRE | BIM-cons | 1.538 | 3.035 | 8.488 | 1.562 | 3.507 | 6.669 | - | - | - |
| GCRE | NTCM-cons | 1.578 | 2.240 | 8.408 | 1.610 | 2.802 | 6.575 | - | - | - |
| GCRE | GIM-cons | 1.541 | 1.962 | 8.316 | 1.599 | 2.753 | 6.517 | - | - | - |
| IF | UC | Ionosphere Constraint | |
|---|---|---|---|
| Observed quantity | 2m+2n+2p+2q | 4m+4n+4p+4q | 5m+5n+5p+5q |
| Parameter number | m+n+p+q+8 | 3m+3n+3p+3q+8 | 3m+3n+3p+3q+12 |
| Redundancy | m+n+p+q−8 | m+n+p+q−8 | 2m+2n+2p+2q−12 |
| Type of the parameters | Position, receiver clock, ZWD, ambiguity | Position, receiver clock, ZWD, slant ionospheric delay, ambiguity | Position, receiver clock, ZWD, DCB, slant ionospheric delay, ambiguity |
| Type | Schemes | b1/b2 | b1/b3 | ||||
|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | ||
| G | IF | 0.905 | 1.613 | 3.147 | - | - | - |
| G | UC | 0.907 | 1.609 | 3.135 | - | - | - |
| G | BIM-cons | 0.878 | 1.595 | 3.162 | - | - | - |
| G | NTCM-cons | 0.905 | 1.587 | 3.159 | - | - | - |
| G | GIM-cons | 0.898 | 1.597 | 3.148 | - | - | - |
| C | IF | 1.435 | 2.490 | 5.679 | 1.560 | 2.954 | 5.886 |
| C | UC | 1.440 | 2.526 | 5.726 | 1.572 | 2.956 | 5.968 |
| C | BIM-cons | 1.360 | 2.374 | 5.535 | 1.390 | 2.464 | 5.828 |
| C | NTCM-cons | 1.387 | 2.309 | 5.488 | 1.398 | 2.444 | 5.692 |
| C | GIM-cons | 1.377 | 2.269 | 5.466 | 1.340 | 2.438 | 5.507 |
| R | IF | 0.917 | 1.873 | 3.303 | - | - | - |
| R | UC | 0.917 | 1.873 | 3.302 | - | - | - |
| R | BIM-cons | 0.944 | 1.875 | 3.472 | - | - | - |
| R | NTCM-cons | 0.944 | 1.889 | 3.434 | - | - | - |
| R | GIM-cons | 0.924 | 1.878 | 3.428 | - | - | - |
| E | IF | 1.028 | 1.809 | 3.566 | 1.109 | 2.099 | 3.364 |
| E | UC | 1.025 | 1.813 | 3.560 | 1.080 | 2.089 | 3.357 |
| E | BIM-cons | 1.040 | 1.805 | 3.486 | 1.066 | 1.918 | 3.306 |
| E | NTCM-cons | 1.030 | 1.771 | 3.404 | 1.097 | 1.847 | 3.318 |
| E | GIM-cons | 1.039 | 1.742 | 3.111 | 1.038 | 1.799 | 3.308 |
| GC | IF | 0.886 | 1.710 | 3.066 | 1.427 | 2.789 | 5.405 |
| GC | UC | 0.892 | 1.708 | 3.056 | 1.425 | 2.774 | 5.393 |
| GC | BIM-cons | 0.870 | 1.581 | 2.946 | 1.330 | 2.367 | 5.426 |
| GC | NTCM-cons | 0.889 | 1.563 | 2.957 | 1.355 | 2.353 | 5.238 |
| GC | GIM-cons | 0.827 | 1.529 | 2.922 | 1.293 | 2.307 | 5.007 |
| GR | IF | 0.811 | 1.525 | 2.903 | - | - | - |
| GR | UC | 0.807 | 1.523 | 2.907 | - | - | - |
| GR | BIM-cons | 0.790 | 1.496 | 2.874 | - | - | - |
| GR | NTCM-cons | 0.817 | 1.487 | 2.757 | - | - | - |
| GR | GIM-cons | 0.771 | 1.372 | 2.718 | - | - | - |
| GE | IF | 0.871 | 1.776 | 3.107 | 1.053 | 2.030 | 3.362 |
| GE | UC | 0.864 | 1.778 | 3.092 | 1.054 | 1.997 | 3.355 |
| GE | BIM-cons | 0.853 | 1.607 | 2.920 | 1.071 | 1.914 | 3.445 |
| GE | NTCM-cons | 0.854 | 1.604 | 2.884 | 1.077 | 1.826 | 3.275 |
| GE | GIM-cons | 0.834 | 1.587 | 2.868 | 0.994 | 1.771 | 3.247 |
| GCR | IF | 0.794 | 1.513 | 2.886 | - | - | - |
| GCR | UC | 0.787 | 1.511 | 2.884 | - | - | - |
| GCR | BIM-cons | 0.782 | 1.428 | 2.818 | - | - | - |
| GCR | NTCM-cons | 0.795 | 1.408 | 2.742 | - | - | - |
| GCR | GIM-cons | 0.755 | 1.305 | 2.701 | - | - | - |
| GCRE | IF | 0.777 | 1.426 | 2.702 | - | - | - |
| GCRE | UC | 0.760 | 1.393 | 2.695 | - | - | - |
| GCRE | BIM-cons | 0.774 | 1.345 | 2.476 | - | - | - |
| GCRE | NTCM-cons | 0.778 | 1.324 | 2.366 | - | - | - |
| GCRE | GIM-cons | 0.676 | 1.286 | 2.347 | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, K.; Jin, S.; Hoque, M.M. Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance. Remote Sens. 2019, 11, 171. https://doi.org/10.3390/rs11020171
Su K, Jin S, Hoque MM. Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance. Remote Sensing. 2019; 11(2):171. https://doi.org/10.3390/rs11020171
Chicago/Turabian StyleSu, Ke, Shuanggen Jin, and M. M. Hoque. 2019. "Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance" Remote Sensing 11, no. 2: 171. https://doi.org/10.3390/rs11020171
APA StyleSu, K., Jin, S., & Hoque, M. M. (2019). Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance. Remote Sensing, 11(2), 171. https://doi.org/10.3390/rs11020171