Refined Two-Stage Programming Approach of Phase Unwrapping for Multi-Baseline SAR Interferograms Using the Unscented Kalman Filter
Abstract
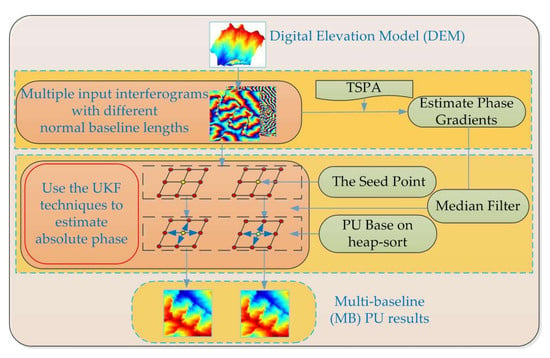
:1. Introduction
2. Review of the TSPA
2.1. Mathematical Foundation of MB PU
2.2. TSPA
3. TSPA-UKFPU Method
3.1. Estimating the Phase Gradient
3.2. UKFPU Algorithm
3.3. Analysis of the Time Complexity
4. Experiments
4.1. Validation Using Simulated Data
4.2. Robustness Analysis Using Simulated Data
4.3. Validation Using Real Data
4.3.1. The Monostatic Data Set
4.3.2. The Bistatic Data Set
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Yu, H.; Lan, Y. Robust two-dimensional phase unwrapping for multibaseline sar interferograms a two-stage programming approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5217–5225. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, Z.; Lin, S.; Liu, T.; Zhang, Q.; Long, T. Local Fringe Frequency Estimation Based on Multifrequency InSAR for Phase-Noise Reduction in Highly Sloped Terrain. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1527–1531. [Google Scholar] [CrossRef]
- Yu, H.; Lan, Y.; Xu, J.; An, D.; Lee, H. Large-Scale L0-Norm and L1-Norm 2-D Phase Unwrapping. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4712–4728. [Google Scholar] [CrossRef]
- Pascazio, V.; Schirinzi, G. Multifrequency InSAR Height Reconstruction Through Maximum Likelihood Estimation of Local Planes Parameters. IEEE Trans. Image Process. 2002, 11, 1478–1489. [Google Scholar] [CrossRef]
- Fornaro, G.; Monti Guarnieri, A.; Pauciullo, A.; De-Zan, F. Maximum likelihood multi-baseline SAR interferometry. In Proceedings of the 2006. IEE Proc. Radar Sonar Navig. 2006, 153, 279–288. [Google Scholar] [CrossRef]
- Fornaro, G.; Pauciullo, A.; Sansosti, E. Phase difference-based multichannel phase unwrapping. IEEE Trans. Image Process. 2005, 14, 960–972. [Google Scholar] [CrossRef] [PubMed]
- Ghiglia, D.C.; Wahl, D.E. Interferometric synthetic aperture radar terrain elevation mapping from multiple observations. In Proceedings of the 1994 IEEE Digital Signal Processing Workshop, Yosemite National Park, CA, USA, 2–5 October 1994; pp. 33–36. [Google Scholar]
- Lombardo, P.; Lombardini, F. Multi-baseline SAR interferometry for terrain slope adaptivity. In Proceedings of the 1997 IEEE National Radar Conference, Syracuse, NY, USA, 13–15 May 1997; pp. 196–201. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Sansosti, E. Bayesian approach to phase-difference-based phase unwrapping. In Proceedings of the 2002 IEEE 36th Asilomar Conference Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2002; pp. 1391–1396. [Google Scholar]
- Poggi, G.; Ragozini, A.R.P.; Servadei, D. A Bayesian Approach for SAR Interferometric Phase Restoration. In Proceedings of the 2000 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; pp. 3202–3205. [Google Scholar]
- Ying, L.; Munson, D.C.; Koetter, R.; Frey, B.J. Multibaseline InSAR terrain elevation estimation: A dynamic programming approach. In Proceedings of the 2003 International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003; pp. 1522–4880. [Google Scholar]
- Ferraiuolo, G.; Pascazio, V.; Schirinzi, G. Maximum a posteriori estimation of height profiles in InSAR imaging. IEEE Geosci. Remote Sens. Lett. 2004, 1, 66–70. [Google Scholar] [CrossRef]
- Ferraioli, G.; Shabou, A.; Tupin, F.; Pascazio, V. Multichannel phase unwrapping with Graph-cuts. IEEE Geosci. Remote Sens. Lett. 2009, 6, 562–566. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G.; Pascazio, V.; Schirinzi, G. Contextual Information-Based Multichannel Synthetic Aperture Radar Interferometry: Addressing DEM reconstruction using contextual information. IEEE Signal Process. Mag. 2014, 31, 59–68. [Google Scholar] [CrossRef]
- Ferraiuolo, G.; Federica, M.; Pascazio, V.; Schirinzi, G. DEM Reconstruction Accuracy in Multichannel SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2009, 47, 191–201. [Google Scholar] [CrossRef]
- Yu, H.; Li, Z.; Bao, Z. A Cluster-Analysis-Based Efficient Multibaseline Phase-Unwrapping Algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 478–487. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, J.; Song, Q.; Zhou, Z. A Refined Cluster-Analysis-Based Multibaseline Phase-Unwrapping Algorithm. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1565–1569. [Google Scholar] [CrossRef]
- Liu, H.; Xing, M.; Bao, Z. A Cluster-Analysis-Based Noise-Robust Phase-Unwrapping Algorithm for Multibaseline Interferograms. IEEE Trans. Geosci. Remote Sens. 2015, 45, 494–504. [Google Scholar] [CrossRef]
- Xu, W.; Chang, E.C.; Kwoh, L.K.; Heng, A. Phase-unwrapping of SAR interferogram with multi-frequency or multi-baseline. In Proceedings of the 1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 730–732. [Google Scholar]
- Yuan, Z.; Deng, Y.; Li, F.; Wang, R.; Liu, G.; Han, X. Multichannel InSAR DEM Reconstruction Through Improved Closed-Form Robust Chinese Remainder Theorem. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1314–1318. [Google Scholar] [CrossRef]
- Wang, W.; Xia, X. A Closed-Form Robust Chinese Remainder Theorem and Its Performance Analysis. IEEE Trans. Image Process. 2010, 58, 5655–5666. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Xia, X. A Fast robust Chinese remainder theorem based phase unwrapping algorithm. IEEE Trans. Signal Process. Lett. 2008, 15, 665–668. [Google Scholar] [CrossRef]
- Thompson, D.G.; Robertson, A.E.; Arnold, D.V.; Long, D.G. Multi-baseline interferometric SAR for iterative height estimation. In Proceedings of the 1999 IEEE International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; pp. 251–253. [Google Scholar]
- Gao, Y.; Zhang, S.; Li, T.; Chen, Q.; Li, S.; Meng, P. Adaptive Unscented Kalman Filter Phase Unwrapping Method and Its Application on Gaofen-3 Interferometric SAR Data. Sensors 2018, 18, 1793. [Google Scholar] [CrossRef]
- Xie, X.; Dai, G. Unscented information filtering phase unwrapping algorithm for interferometric fringe patterns. Appl. Opt. 2017, 56, 9423–9434. [Google Scholar] [CrossRef]
- Kim, M.G.; Griffiths, H.D. Phase unwrapping of multibaseline interferometry using Kalman filtering. In Proceedings of the 7th 1999 International Conference on Image Processing and Its Applications, February Manchester, UK, 13–15 July 1999; pp. 813–817. [Google Scholar]
- Xie, X.; Pi, Y. Multi-baseline phase unwrapping algorithm based on the unscented Kalman filter. IET Radar Sonar Navig. 2011, 5, 296–304. [Google Scholar] [CrossRef]
- Xie, X. Multi-baseline UKF phase unwrapping algorithm via joint phase slope estimator. IEICE Commun. Express 2014, 3, 20–26. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Yu, W.; Wang, R.; Liu, G.; Shao, Y. Integrated Denoising and Unwrapping of InSAR Phase Based on Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4473–4485. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Valadão, G. Phase Unwrapping via Graph Cuts. IEEE Trans. Image Process. 2007, 16, 698–709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wyant, J.C. Testing aspherics using two-wavelength holography. Appl. Opt. 1971, 10, 2113–2118. [Google Scholar] [CrossRef] [PubMed]
- Servin, M.; Padilla, M.; Garnica, G. Super-sensitive two-wavelength fringe projection profilometry with 2-sensitivities temporal unwrapping. Opt. Lasers Eng. 2018, 106, 68–74. [Google Scholar] [CrossRef] [Green Version]








| Orbit Altitude | Incidence Angle | Wavelength |
|---|---|---|
| 600 km | 30° | 0.24 m |
| Interferogram | Figure 4b | Figure 4c |
| Normal Baseline | 389.20 m | 112.10 m |
| Image Size | 458 × 157 pixels | 458 × 157 pixels |
| Orbit Altitude | Incidence Angle | Wavelength |
|---|---|---|
| 691.65 km | 34.30° | 0.2360 m |
| Interferogram | Figure 6b | Figure 6c |
| Normal Baseline | 193.17 m | 101.57 m |
| Image Size | 800 × 800 pixels | 800 × 800 pixels |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Zhang, S.; Li, T.; Chen, Q.; Zhang, X.; Li, S. Refined Two-Stage Programming Approach of Phase Unwrapping for Multi-Baseline SAR Interferograms Using the Unscented Kalman Filter. Remote Sens. 2019, 11, 199. https://doi.org/10.3390/rs11020199
Gao Y, Zhang S, Li T, Chen Q, Zhang X, Li S. Refined Two-Stage Programming Approach of Phase Unwrapping for Multi-Baseline SAR Interferograms Using the Unscented Kalman Filter. Remote Sensing. 2019; 11(2):199. https://doi.org/10.3390/rs11020199
Chicago/Turabian StyleGao, YanDong, ShuBi Zhang, Tao Li, QianFu Chen, Xiang Zhang, and ShiJin Li. 2019. "Refined Two-Stage Programming Approach of Phase Unwrapping for Multi-Baseline SAR Interferograms Using the Unscented Kalman Filter" Remote Sensing 11, no. 2: 199. https://doi.org/10.3390/rs11020199
APA StyleGao, Y., Zhang, S., Li, T., Chen, Q., Zhang, X., & Li, S. (2019). Refined Two-Stage Programming Approach of Phase Unwrapping for Multi-Baseline SAR Interferograms Using the Unscented Kalman Filter. Remote Sensing, 11(2), 199. https://doi.org/10.3390/rs11020199