Autonomous Airborne 3D SAR Imaging System for Subsurface Sensing: UWB-GPR on Board a UAV for Landmine and IED Detection
Abstract
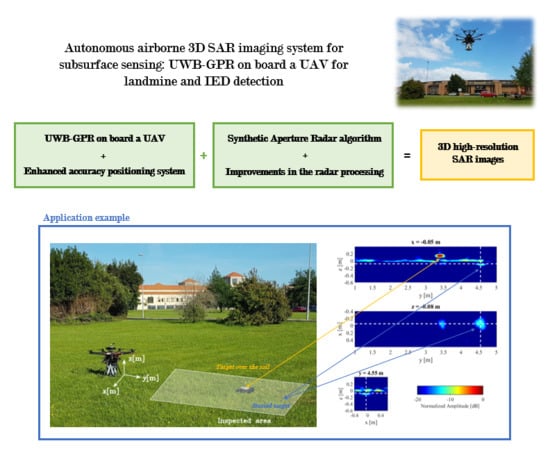
:1. Introduction
2. System Architecture
- The flight control subsystem is composed of the UAV flight controller and common positioning sensors on board UAVs. These sensors are: an Inertial Measurement Unit (IMU), a barometer, and a Global Navigation Satellite System (GNSS) receiver.
- The enhanced positioning system consists of a laser rangefinder and a dual-band Real Time Kinematic (RTK) system.
- The radar subsystem includes the radar module, and the transmitter and receiver antennas.
- The communication subsystem has a receiver at 433 MHz for the link with the pilot remote controller and a wireless local area network (WLAN) transceiver at GHz to exchange data with the ground station. Both frequencies were selected to minimize possible interferences with the radar subsystem during the experimental campaigns.
3. Methodology
3.1. Positioning Data Processing
- , where and are the differences between adjacent values of and , respectively. This condition ensures that the UAV is actually moving.
- , , and , where denotes the mean value. These conditions are used to filter out the positions where there was a noticeable change in attitude.
- , where denotes the remainder operator. Only measurements with the course over ground close to the main one are kept. This means that, if the UAV path deviates noticeably from the main path, these measurements are discarded.
- . This condition helps to get rid of considerable changes in height.
- First, the minimum area bounding rectangle that encloses the observation plane (called bounding box) is retrieved. To find it, the convex hull of the observation plane coordinates (i.e., the smallest convex polygon containing the observation plane) is computed. Then, the bounding box can be easily obtained since it always contains an edge of the convex hull.
- Then, the maximum axis-aligned rectangle inside the bounding box is computed, since it is easy to define and work with an axis-aligned investigation domain and the observation domain is almost aligned (due to the rotation according to the main course over the ground previously performed).
- Finally, the investigation plane is defined by shrinking this rectangle by a scale factor of and in the track and across-track directions (to avoid edge effects in the SAR image) and sampling it every and , respectively.
3.2. Radar Data Processing
4. Results and Discussion
4.1. Basic Processing
4.2. Enhanced Processing
4.2.1. Height Correction
4.2.2. Equalization
4.2.3. Height Correction and Equalization
4.2.4. Soil Composition Consideration
4.3. Comparison
5. Conclusions
6. Patents
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yao, H.; Qin, R.; Chen, X. Unmanned Aerial Vehicle for Remote Sensing Applications—A Review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Hildmann, H.; Kovacs, E. Review: Using Unmanned Aerial Vehicles (UAVs) as Mobile Sensing Platforms (MSPs) for Disaster Response, Civil Security and Public Safety. Drones 2019, 3, 59. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Jeziorska, J. UAs for Wetland Mapping and Hydrological Modeling. Remote Sens. 2019, 11, 1997. [Google Scholar] [CrossRef]
- Garcia-Fernandez, M.; Alvarez-Lopez, Y.; Las Heras, F. On the use of Unmanned Aerial Vehicles for antenna and coverage diagnostics in mobile networks. IEEE Commun. Mag. 2018, 56, 72–78. [Google Scholar] [CrossRef]
- Llort, M.; Aguasca, A.; Lopez-Martinez, C.; Martinez-Marin, T. Initial evaluation of SAR capabilities in UAV multicopter platforms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 127–140. [Google Scholar] [CrossRef]
- Garcia-Fernandez, M.; Alvarez-Lopez, Y.; Arboleya-Arboleya, A.; Gonzalez-Valdes, B.; Rodriguez-Vaqueiro, Y.; Las Heras, F.; Pino, A. Synthetic Aperture Radar imaging system for landmine detection using a Ground Penetrating Radar on board an Unmanned Aerial Vehicle. IEEE Access 2018, 6, 45100–45112. [Google Scholar] [CrossRef]
- Robledo, L.; Carrasco, M.; Mery, D. A survey of land mine detection technology. Int. J. Remote Sens. 2009, 30, 2399–2410. [Google Scholar] [CrossRef]
- Jol, H.M. Ground Penetrating Radar Theory and Applications; Elsevier Science: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Daniels, D.J. A review of GPR for landmine detection. Sens. Imaging Int. J. 2006, 7, 90–123. [Google Scholar] [CrossRef]
- Rappaport, C.; El-Shenawee, M.; Zhan, H. Suppressing GPR clutter from randomly rough ground surfaces to enhance nonmetallic mine detection. Subsurf. Sens. Technol. Appl. 2003, 4, 311–326. [Google Scholar] [CrossRef]
- Wang, T.; Keller, J.M.; Gader, P.D.; Sjahputera, O. Frequency subband processing and feature analysis of forward-looking ground-penetrating radar signals for land-mine detection. IEEE Trans. Geosci. Remote Sens. 2007, 45, 718–729. [Google Scholar] [CrossRef]
- Peichl, M.; Schreiber, E.; Heinzel, A.; Kempf, T. TIRAMI-SAR—A Synthetic Aperture Radar approach for efficient detection of landmines and UXO. In Proceedings of the 10th European Conference on Synthetic Aperture Radar—EuSAR, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Comite, D.; Galli, A.; Catapano, I.; Soldovieri, F. Advanced imaging for down-looking contactless GPR systems. In Proceedings of the International Applied Computational Electromagnetics Society Symposium—Italy (ACES), Florence, Italy, 26–30 March 2017. [Google Scholar]
- Gonzalez-Valdes, B.; Alvarez-Lopez, Y.; Arboleya, A.; Rodriguez-Vaqueiro, Y.; Garcia-Fernandez, M.; Las Heras, F.; Pino, A. Airborne Systems and Methods for the Detection, Localisation and Imaging of Buried Objects, and Characterization of the Subsurface Composition. ES Patent 2,577,403 (WO2017/125627), 21 January 2016. [Google Scholar]
- Fasano, G.; Renga, A.; Vetrella, A.R.; Ludeno, G.; Catapano, I.; Soldovieri, F. Proof of concept of micro-UAV-based radar imaging. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017. [Google Scholar]
- Schartel, M.; Bähnemann, R.; Burr, R.; Mayer, W.; Waldschmidt, C. Position acquisition for a multicopter-based synthetic aperture radar. In Proceedings of the 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019. [Google Scholar]
- Alvarez-Narciandi, G.; Lopez-Portuges, M.; Las-Heras, F.; Laviada, J. Freehand, Agile and High-Resolution Imaging With Compact mm-Wave Radar. IEEE Access 2019, 7, 95516–95526. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, M.; Garcia-Fernandez, M.; Alvarez-Lopez, Y.; Las Heras, F. Improvement of GPR SAR-based techniques for accurate detection and imaging of buried objects. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
- Topcon B111 Receiver. Available online: https://www.topconpositioning.com/oem-components-technology/gnss-components/b111 (accessed on 31 August 2019).
- Solimene, R.; Cuccaro, A.; Dell’Aversano, A.; Catapano, I.; Soldovieri, F. Ground clutter removal in gpr surveys. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 792–798. [Google Scholar] [CrossRef]
- Johansson, E.M.; Mast, J.E. Three-dimensional ground-penetrating radar imaging using synthetic aperture time-domain focusing. In Proceedings of the International Symposium on Optics, Imaging, and Instrumentation, International Society for Optics and Photonics, San Diego, CA, USA, 14 September 1994. [Google Scholar]
- Fuse, Y.; Gonzalez-Valdes, B.; Martinez-Lorenzo, J.A.; Rappaport, C.M. Advanced SAR imaging methods for forward-looking ground penetrating radar. In Proceedings of the European Conference on Antennas and Propagation, Davos, Switzerland, 10–15 April 2016. [Google Scholar]
- Alvarez, Y.; Garcia-Fernandez, M.; Arboleya-Arboleya, A.; Gonzalez-Valdes, B.; Rodriguez-Vaqueiro, Y.; Las-Heras, F.; Pino, A. SAR-based technique for soil permittivity estimation. Int. J. Remote Sens. 2017, 38, 5168–5186. [Google Scholar] [CrossRef]



















© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Fernandez, M.; Alvarez-Lopez, Y.; Las Heras, F. Autonomous Airborne 3D SAR Imaging System for Subsurface Sensing: UWB-GPR on Board a UAV for Landmine and IED Detection. Remote Sens. 2019, 11, 2357. https://doi.org/10.3390/rs11202357
Garcia-Fernandez M, Alvarez-Lopez Y, Las Heras F. Autonomous Airborne 3D SAR Imaging System for Subsurface Sensing: UWB-GPR on Board a UAV for Landmine and IED Detection. Remote Sensing. 2019; 11(20):2357. https://doi.org/10.3390/rs11202357
Chicago/Turabian StyleGarcia-Fernandez, Maria, Yuri Alvarez-Lopez, and Fernando Las Heras. 2019. "Autonomous Airborne 3D SAR Imaging System for Subsurface Sensing: UWB-GPR on Board a UAV for Landmine and IED Detection" Remote Sensing 11, no. 20: 2357. https://doi.org/10.3390/rs11202357
APA StyleGarcia-Fernandez, M., Alvarez-Lopez, Y., & Las Heras, F. (2019). Autonomous Airborne 3D SAR Imaging System for Subsurface Sensing: UWB-GPR on Board a UAV for Landmine and IED Detection. Remote Sensing, 11(20), 2357. https://doi.org/10.3390/rs11202357