Super-Resolution of Remote Sensing Images via a Dense Residual Generative Adversarial Network
Abstract
:1. Introduction
2. Related Work
2.1. GAN-Based SR
2.2. Residual Learning-Based SR
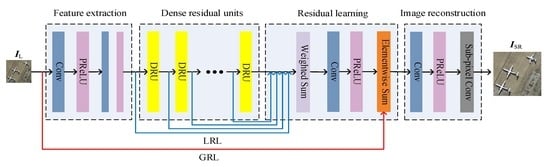
3. Proposed Method
3.1. Structure of the GN
3.1.1. Feature Extraction
3.1.2. DRUs
3.1.3. Residual Learning
3.1.4. Image Reconstruction
- 1)
- Convolution. Similar to the previous convolution layers in the GN, this step is used to extract features. The difference between them is that there are feature maps according to the upscaling factor .
- 2)
- Arrangement. Arrange all the pixels in the corresponding position of feature maps in a predetermined order in order to combine them into a series of areas. The size of each area is . Each area corresponds to a mini-patch in the final SR image . In this manner, we rearrange the final feature maps of size into of size . This implementation equals the rearrangement of the image without convolution operations, and thus, requires very little time.
3.2. Structure of the DN
3.3. Loss Function
- 1)
- Feed the LR image into the GN, obtain the corresponding reconstructed image and compute the content loss based on the MSE.
- 2)
- Import the reconstructed image and the corresponding ground-truth image into VGG, and extract the respective high-level features.
- 3)
- Feed the extracted feature maps into the DN and obtain the adversarial loss. The final loss is computed as the weighted sum of the content loss and the adversarial loss .
- 4)
- Implement the backward process of the network and compute the gradients of each layer. Optimize the network iteratively by updating the parameters in the DN and GN according to the training policy.
- 5)
- Repeat the above steps until reaching the minimum loss of the network, and then the work of training the network is finished.
4. Experiments
4.1. Dataset
4.2. Training Details
4.3. Quantitative Evaluation Factors
4.3.1. Peak Signal-To-Noise Ratio (PSNR)
4.3.2. Structural Similarity Index (SSIM)
4.3.3. Normalized Root Mean Square Error (NRMSE)
4.3.4. Erreur Relative Globale Adimensionnelle De Synthese (ERGAS)
5. Results
6. Discussion
6.1. The Effect of Adding MSE into the Loss Function
6.2. The Impact of Using or on Our SR Model
6.3. Robustness of the Model
6.4. Future Work
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wilman, W.W.Z.; Yuen, P.C. Very low resolution face recognition problem. IEEE Trans. Image Process. 2010, 21, 327–340. [Google Scholar]
- Thornton, M.W.; Atkinson, P.M.; Holland, D.A. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping. Int. J. Remote Sens. 2006, 27, 473–491. [Google Scholar] [CrossRef]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.-H.; Zhang, L.; Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M.; et al. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1110–1121. [Google Scholar]
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP Graph. Model. Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Su, H.; Zhou, J.; Zhang, Z. Survey of super-resolution image reconstruction methods. Acta Autom. Sin. 2013, 39, 1202–1213. [Google Scholar] [CrossRef]
- Yang, C.-Y.; Ma, C.; Yang, M.-H. Single-Image Super-Resolution: A Benchmark. Model Data Eng. 2014, 8692, 372–386. [Google Scholar]
- Freedman, G.; Fattal, R. Image and video up-scaling from local self-examples. ACM Trans. Graph. 2011, 2, 12. [Google Scholar]
- Yang, J.; Lin, Z.; Cohen, S. Fast Image Super-Resolution Based on In-Place Example Regression. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1059–1066. [Google Scholar]
- Kim, K.I.; Kwon, Y. Single-Image Super-Resolution Using Sparse Regression and Natural Image Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar]
- Chang, H.; Yeung, D.Y.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 275–282. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Li, F.; Jia, X.; Fraser, D.; Lambert, A. Super resolution for remote sensing images based on a universal hidden Markov tree model. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1270–1278. [Google Scholar]
- Pan, Z.; Yu, J.; Huang, H.; Hu, S.; Zhang, A.; Ma, H.; Sun, W. Super-Resolution Based on Compressive Sensing and Structural Self-Similarity for Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4864–4876. [Google Scholar] [CrossRef]
- Timofte, R.; Smet, V.; Gool, L.V. Anchored neighborhood regression for fast example-based super-resolution. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 1920–1927. [Google Scholar]
- Timofte, R.; Smet, D.; Gool, L.V. A+: Adjusted anchored neighborhood regression for fast super-resolution. In Proceedings of the Asian Conference on Computer Vision (ACCV), Singapore, 1–5 November 2014; pp. 111–126. [Google Scholar]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the IEEE 12th international conference on computer vision, Kyoto, Japan, 29 September–2 October 2009; pp. 349–356. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Perez-Pellitero, E.; Salvador, J.; Ruiz-Hidalgo, J.; Rosenhahn, B. PSyCo: Manifold Span Reduction for Super Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1837–1845. [Google Scholar]
- Salvador, J.; Perezpellitero, E. Naive Bayes Super-Resolution Forest. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2380–7504. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In Proceedings of the Computer Vision–ECCV, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Berlin, Germany, 2014; pp. 184–199. [Google Scholar]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the Super-Resolution Convolutional Neural Network. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; Volume 9906, pp. 391–407. [Google Scholar]
- Zhao, X.; Zhang, Y.; Zhang, T.; Zou, X. Channel Splitting Network for Single MR Image Super-Resolution. IEEE Trans. Image Process. 2019, 28, 5649–5662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muqeet, A.; Bin Iqbal, M.T.; Bae, S.-H. HRAN: Hybrid Residual Attention Network for Single Image Super-Resolution. IEEE Access 2019, 7, 137020–137029. [Google Scholar] [CrossRef]
- Zhao, F.; Si, W.; Dou, Z. Image super-resolution via two stage coupled dictionary learning. Multimedia Tools Appl. 2017, 78, 28453–28460. [Google Scholar] [CrossRef]
- Li, F.; Bai, H.; Zhao, Y. Detail-preserving image super-resolution via recursively dilated residual network. Neurocomputing 2019, 358, 285–293. [Google Scholar] [CrossRef]
- He, H.; Chen, T.; Chen, M.; Li, D.; Cheng, P. Remote sensing image super-resolution using deep–shallow cascaded convolutional neural networks. Sens. Rev. 2019, 39, 629–635. [Google Scholar] [CrossRef]
- Ma, W.; Pan, Z.; Guo, J.; Lei, B. Achieving Super-Resolution Remote Sensing Images via the Wavelet Transform Combined With the Recursive Res-Net. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3512–3527. [Google Scholar] [CrossRef]
- Zhang, T.; Du, Y.; Lu, F. Super-Resolution Reconstruction of Remote Sensing Images Using Multiple-Point Statistics and Isometric Mapping. Remote Sens. 2017, 9, 724. [Google Scholar] [CrossRef]
- Gu, J.; Sun, X.; Zhang, Y.; Fu, K.; Wang, L. Deep Residual Squeeze and Excitation Network for Remote Sensing Image Super-Resolution. Remote Sens. 2019, 11, 1817. [Google Scholar] [CrossRef]
- He, Z.; Liu, L. Hyperspectral Image Super-Resolution Inspired by Deep Laplacian Pyramid Network. Remote Sens. 2018, 10, 1939. [Google Scholar] [CrossRef]
- Kwan, C.; Choi, J.H.; Chan, S.H.; Zhou, J.; Budavari, B. A Super-Resolution and Fusion Approach to Enhancing Hyperspectral Images. Remote Sens. 2018, 10, 1416. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; Shi, W. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ma, W.; Pan, Z.; Guo, J.; Lei, B. Super-Resolution of Remote Sensing Images Based on Transferred Generative Adversarial Network. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1148–1151. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. Available online: https://arxiv.org/abs/1511.06434 (accessed on 1 August 2019).
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. Available online: https://arxiv.org/abs/1701.07875 (accessed on 1 August 2019).
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved Training of Wasserstein GANs. Available online: https://arxiv.org/abs/1704.00028 (accessed on 1 August 2019).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the NIPS, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 2–5. [Google Scholar]
- Jiwon, K.; Jung, K.L.; Kyoung, M.L. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Jiwon, K.; Jung, K.L.; Kyoung, M.L. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar]
- Nah, S.; Kim, T.; Lee, K. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 257–265. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on Image Net Classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. Lecture 6.5-RmsProp: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. International Conference on Pattern Recognition. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Veganzones, M.A.; Simoes, M.; Licciardi, G.; Yokoya, N.; Bioucas-Dias, J.M.; Chanussot, J. Hyperspectral super-resolution of locally low rank images from complementary multisource data. IEEE Trans. Image Process. 2016, 25, 274–288. [Google Scholar] [CrossRef]
- Bevilacqua, C.M.; Roumy, A.; Morel, M.-L.A. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the BMVC, Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 416–423. [Google Scholar]
- Huang, J.-B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
















| Title | Scale | Bicubic | SRCNN | FSRCNN | ESPCN | VDSR | DRRN | SRGAN | DRGAN (ours) |
|---|---|---|---|---|---|---|---|---|---|
| airplane _001 | ×2 | 29.99 | 32.85 | 33.72 | 33.23 | 34.14 | 34.34 | -/- | 34.62 |
| ×3 | 26.95 | 28.84 | 29.59 | 29.21 | 30.29 | 30.45 | -/- | 30.69 | |
| ×4 | 25.21 | 26.45 | 26.94 | 26.68 | 27.66 | 27.88 | 26.25 | 28.11 | |
| airplane _035 | ×2 | 30.36 | 32.75 | 33.22 | 32.92 | 33.45 | 33.63 | -/- | 33.91 |
| ×3 | 27.36 | 29.02 | 29.21 | 29.15 | 29.78 | 29.94 | -/- | 30.16 | |
| ×4 | 25.78 | 27.20 | 27.69 | 27.32 | 28.02 | 28.19 | 27.03 | 28.48 | |
| airplane _095 | ×2 | 27.98 | 29.86 | 30.36 | 30.08 | 30.69 | 30.86 | -/- | 30.15 |
| ×3 | 25.34 | 26.54 | 26.95 | 26.80 | 27.31 | 27.54 | -/- | 27.80 | |
| ×4 | 24.02 | 24.87 | 25.11 | 25.00 | 25.36 | 25.53 | 24.69 | 25.83 | |
| Test dataset | ×2 | 32.20 | 34.37 | 34.96 | 34.63 | 35.12 | 35.33 | -/- | 35.56 |
| ×3 | 29.09 | 30.59 | 31.15 | 30.87 | 31.47 | 31.70 | -/- | 31.92 | |
| ×4 | 27.42 | 28.43 | 28.92 | 28.68 | 29.31 | 29.55 | 27.99 | 29.76 |
| Title | Scale | Bicubic | SRCNN | FSRCNN | ESPCN | VDSR | DRRN | SRGAN | DRGAN (ours) |
|---|---|---|---|---|---|---|---|---|---|
| airplane _001 | ×2 | 0.9160 | 0.9489 | 0.9539 | 0.9515 | 0.9563 | 0.9583 | -/- | 0.9661 |
| ×3 | 0.8350 | 0.8768 | 0.8893 | 0.8826 | 0.9013 | 0.9089 | -/- | 0.9196 | |
| ×4 | 0.7681 | 0.8035 | 0.8187 | 0.8111 | 0.8422 | 0.8512 | 0.8063 | 0.8622 | |
| airplane _035 | ×2 | 0.9401 | 0.9645 | 0.9697 | 0.9655 | 0.9709 | 0.9745 | -/- | 0.9811 |
| ×3 | 0.8693 | 0.9074 | 0.9210 | 0.9101 | 0.9381 | 0.9396 | -/- | 0.9460 | |
| ×4 | 0.8053 | 0.8494 | 0.8676 | 0.8477 | 0.8950 | 0.9012 | 0.8554 | 0.9143 | |
| airplane _095 | ×2 | 0.8750 | 0.9152 | 0.9217 | 0.9190 | 0.9273 | 0.9338 | -/- | 0.9432 |
| ×3 | 0.7708 | 0.8151 | 0.8307 | 0.8243 | 0.8444 | 0.8522 | -/- | 0.8628 | |
| ×4 | 0.7005 | 0.7369 | 0.7519 | 0.7460 | 0.7711 | 0.7802 | 0.7378 | 0.7908 | |
| Test dataset | ×2 | 0.9042 | 0.9346 | 0.9397 | 0.9372 | 0.9435 | 0.9497 | -/- | 0.9631 |
| ×3 | 0.8232 | 0.8582 | 0.8692 | 0.8644 | 0.8810 | 0.8904 | -/- | 0.9102 | |
| ×4 | 0.7623 | 0.7918 | 0.8045 | 0.7995 | 0.8240 | 0.8369 | 0.7933 | 0.8544 |
| Title | Scale | Bicubic | SRCNN | FSRCNN | ESPCN | VDSR | DRRN | SRGAN | DRGAN (ours) |
|---|---|---|---|---|---|---|---|---|---|
| airplane _001 | ×2 | 0.0317 | 0.0211 | 0.0206 | 0.0218 | 0.0196 | 0.0192 | -/- | 0.0186 |
| ×3 | 0.0450 | 0.0362 | 0.0355 | 0.0346 | 0.0306 | 0.0300 | -/- | 0.0292 | |
| ×4 | 0.0549 | 0.0476 | 0.0449 | 0.0464 | 0.0414 | 0.0404 | 0.0487 | 0.0393 | |
| airplane _035 | ×2 | 0.0304 | 0.0230 | 0.0218 | 0.0226 | 0.0213 | 0.0208 | -/- | 0.0201 |
| ×3 | 0.0429 | 0.0354 | 0.0334 | 0.0349 | 0.0324 | 0.0318 | -/- | 0.0310 | |
| ×4 | 0.0514 | 0.0437 | 0.0413 | 0.0431 | 0.0397 | 0.0389 | 0.0445 | 0.0377 | |
| airplane _095 | ×2 | 0.0399 | 0.0321 | 0.0303 | 0.0313 | 0.0292 | 0.0286 | -/- | 0.0311 |
| ×3 | 0.0541 | 0.0471 | 0.0449 | 0.0457 | 0.0431 | 0.0420 | -/- | 0.0407 | |
| ×4 | 0.0629 | 0.0571 | 0.0555 | 0.0563 | 0.0539 | 0.0529 | 0.0583 | 0.0511 | |
| Test dataset | ×2 | 0.0273 | 0.0215 | 0.0201 | 0.0209 | 0.0195 | 0.0171 | -/- | 0.0167 |
| ×3 | 0.0382 | 0.0323 | 0.0304 | 0.0314 | 0.0293 | 0.0260 | -/- | 0.0254 | |
| ×4 | 0.0459 | 0.0408 | 0.0387 | 0.0398 | 0.0371 | 0.0333 | 0.0399 | 0.0325 |
| Title | Scale | Bicubic | SRCNN | FSRCNN | ESPCN | VDSR | DRRN | SRGAN | DRGAN (ours) |
|---|---|---|---|---|---|---|---|---|---|
| airplane _001 | ×2 | 3.6583 | 2.6447 | 2.3910 | 2.5311 | 2.2697 | 2.1977 | -/- | 2.0831 |
| ×3 | 3.4587 | 2.7844 | 2.5551 | 2.6733 | 2.3535 | 2.2882 | -/- | 2.1940 | |
| ×4 | 3.1679 | 2.7466 | 2.5948 | 2.6816 | 2.3907 | 2.3011 | 2.6216 | 2.2354 | |
| airplane _035 | ×2 | 4.5529 | 3.4659 | 3.2829 | 3.3995 | 3.1908 | 3.1116 | -/- | 2.9958 |
| ×3 | 4.3017 | 3.5533 | 3.3545 | 3.5144 | 3.2527 | 3.1998 | -/- | 3.0587 | |
| ×4 | 3.8641 | 3.2866 | 3.1039 | 3.2488 | 2.9900 | 2.8045 | 3.0587 | 2.7582 | |
| airplane _095 | ×2 | 4.0629 | 3.2816 | 3.0968 | 3.2021 | 2.9791 | 2.9877 | -/- | 2.8653 |
| ×3 | 3.6805 | 3.2110 | 3.0617 | 3.1190 | 2.9353 | 2.9122 | -/- | 2.8800 | |
| ×4 | 3.2179 | 2.9187 | 2.8388 | 2.8827 | 2.7590 | 2.6654 | 2.8252 | 2.6029 | |
| Test dataset | ×2 | 3.1608 | 2.5015 | 2.3451 | 2.4345 | 2.2666 | 2.2081 | -/- | 2.1630 |
| ×3 | 2.9462 | 2.4996 | 2.3551 | 2.4379 | 2.2613 | 2.2475 | -/- | 2.1815 | |
| ×4 | 2.6522 | 2.3634 | 2.2415 | 2.3107 | 2.1469 | 2.0998 | 2.2973 | 2.0764 |
| Title | Scale | Bicubic | SRCNN | FSRCNN | ESPCN | VDSR | DRRN | SRGAN | DRGAN (ours) |
|---|---|---|---|---|---|---|---|---|---|
| airplane _001 | ×2 | 0.0000 | 0.1297 | 0.0369 | 0.0319 | 1.7643 | 0.2157 | -/- | 0.1638 |
| ×3 | 0.0000 | 0.1277 | 0.0189 | 0.0170 | 1.7264 | 0.2153 | -/- | 0.1619 | |
| ×4 | 0.0000 | 0.1287 | 0.0109 | 0.0120 | 1.7762 | 0.2154 | 0.7515 | 0.1610 | |
| airplane _035 | ×2 | 0.0000 | 0.1267 | 0.0339 | 0.0309 | 1.7513 | 0.2389 | -/- | 0.1820 |
| ×3 | 0.0000 | 0.1316 | 0.0180 | 0.0170 | 1.7234 | 0.2374 | -/- | 0.1816 | |
| ×4 | 0.0000 | 0.1297 | 0.0100 | 0.0120 | 1.7563 | 0.2365 | 0.7550 | 0.1814 | |
| airplane _095 | ×2 | 0.0000 | 0.1316 | 0.0329 | 0.0299 | 1.7982 | 0.2268 | -/- | 0.0410 |
| ×3 | 0.0000 | 0.1267 | 0.0160 | 0.0159 | 1.7254 | 0.2070 | -/- | 0.0382 | |
| ×4 | 0.0000 | 0.1466 | 0.0100 | 0.0100 | 1.7663 | 0.2099 | 0.7587 | 0.0394 | |
| Test dataset | ×2 | 0.0000 | 0.1303 | 0.0337 | 0.0300 | 1.7961 | 0.2386 | -/- | 0.1621 |
| ×3 | 0.0000 | 0.1278 | 0.0158 | 0.0156 | 1.7442 | 0.2173 | -/- | 0.1657 | |
| ×4 | 0.0000 | 0.1371 | 0.0096 | 0.0102 | 1.7689 | 0.2102 | 0.7647 | 0.1539 |
| Title | Scale | BicubicPSNR/SSIM | SRCNNPSNR/SSIM | SRGANPSNR/SSIM | DRGANPSNR/SSIM |
|---|---|---|---|---|---|
| Set5 | × 2 | 33.66/0.9299 | 36.66/0.9542 | -/- | 36.98/0.9602 |
| × 3 | 30.39/0.8682 | 32.75/0.9090 | -/- | 33.11/0.9130 | |
| × 4 | 28.42/0.8104 | 30.49/0.8628 | 29.40/0.8472 | 30.86/0.8712 | |
| Set14 | × 2 | 30.23/0.8687 | 32.45/0.9067 | -/- | 32.81/0.9118 |
| × 3 | 27.54/0.7736 | 29.30/0.8215 | -/- | 29.65/0.8286 | |
| × 4 | 26.00/0.7019 | 27.50/0.7513 | 26.02/0.7397 | 27.89/0.7655 | |
| BSD100 | × 2 | 29.56/0.8431 | 31.36/0.8879 | -/- | 31.91/0.8936 |
| × 3 | 27.21/0.7385 | 28.41/0.7863 | -/- | 28.77/0.7951 | |
| × 4 | 25.96/0.6675 | 26.90/0.7101 | 25.16/0.6688 | 27.22/0.7268 | |
| Urban100 | × 2 | 26.88/0.8403 | 29.50/0.8946 | -/- | 30.02/0.9024 |
| × 3 | 24.46/0.7349 | 26.24/0.7989 | -/- | 26.56/0.8031 | |
| × 4 | 23.14/0.6577 | 24.52/0.7221 | 23.98/0.6935 | 24.90/0.7356 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Pan, Z.; Yuan, F.; Lei, B. Super-Resolution of Remote Sensing Images via a Dense Residual Generative Adversarial Network. Remote Sens. 2019, 11, 2578. https://doi.org/10.3390/rs11212578
Ma W, Pan Z, Yuan F, Lei B. Super-Resolution of Remote Sensing Images via a Dense Residual Generative Adversarial Network. Remote Sensing. 2019; 11(21):2578. https://doi.org/10.3390/rs11212578
Chicago/Turabian StyleMa, Wen, Zongxu Pan, Feng Yuan, and Bin Lei. 2019. "Super-Resolution of Remote Sensing Images via a Dense Residual Generative Adversarial Network" Remote Sensing 11, no. 21: 2578. https://doi.org/10.3390/rs11212578
APA StyleMa, W., Pan, Z., Yuan, F., & Lei, B. (2019). Super-Resolution of Remote Sensing Images via a Dense Residual Generative Adversarial Network. Remote Sensing, 11(21), 2578. https://doi.org/10.3390/rs11212578