Modeling Population Density Using a New Index Derived from Multi-Sensor Image Data
Abstract
:1. Introduction
2. Data and Method
2.1. Data Collection and Preprocessing
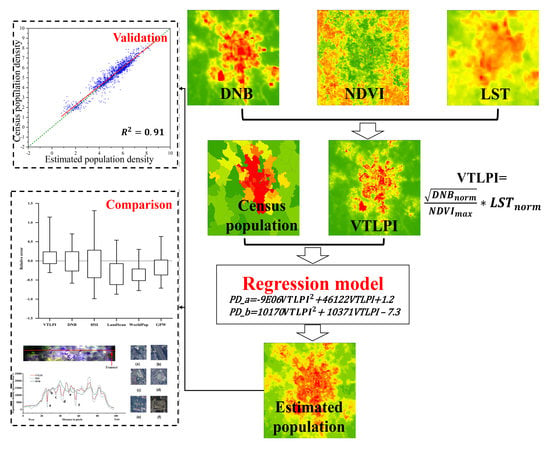
2.2. Vegetation Temperature Light Population Index
2.3. Elevation Correction of VTLPI
2.4. Modeling of Population Density based on VTLPI
2.5. Validation
3. Results
3.1. Implementation of the Proposed Model
3.2. Accuracy Assessment
3.3. Comparison with Other Methods
3.3.1. Comparative Analysis at the County and Township Levels
3.3.2. Comparison of Specific Spatial Locations
4. Discussion
4.1. Performance of VTLPI for Population Estimation
4.2. Regression Analysis Versus Dasymetric Mapping
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A1. Determination of Parameter C

Appendix A2. Regression Analysis in Region A and B

Appendix A3. The Latitudinal Transect in the Chengdu City

Appendix A4. Comparison of Population Density in the Wenchuan County

References
- Hay, S.I.; Noor, A.M.; Nelson, A.; Tatem, A.J. The accuracy of human population maps for public health application. Trop. Med. Int. Health 2005, 10, 1073–1086. [Google Scholar] [CrossRef] [PubMed]
- Ahola, T.; Virrantaus, K.; Krisp, J.M.; Hunter, G.J.; Ahola, T.; Virrantaus, K.; Krisp, J.M.; Hunter, G.J. A spatio-Temporal population model to support risk assessment and damage analysis for decision-making. Int. J. Geogr. Inf. Sci. 2007, 21, 935–953. [Google Scholar] [CrossRef]
- Aubrecht, C.; Özceylan, D.; Steinnocher, K.; Freire, S. Multi-level geospatial modeling of human exposure patterns and vulnerability indicators. Nat. Hazards 2013, 68, 147–163. [Google Scholar] [CrossRef]
- Jia, P.; Qiu, Y.; Gaughan, A.E. A fine-scale spatial population distribution on the High-resolution Gridded Population Surface and application in Alachua County, Florida. Appl. Geogr. 2014, 50, 99–107. [Google Scholar] [CrossRef]
- Yang, X.; Yue, W.; Gao, D. Spatial improvement of human population distribution based on multi-sensor remote-sensing data: An input for exposure assessment. Int. J. Remote Sens. 2013, 34, 5569–5583. [Google Scholar] [CrossRef]
- Yang, X.; Huang, Y.; Dong, P.; Jiang, D.; Liu, H. An updating system for the gridded population database of china based on remote sensing, GIS and spatial database technologies. Sensors 2009, 9, 1128–1140. [Google Scholar] [CrossRef]
- Roy Chowdhury, P.K.; Maithani, S.; Dadhwal, V.K. To Estimation of urban population in Indo-Gangetic Plains using night-time OLS data. Int. J. Remote Sens. 2012, 33, 2498–2515. [Google Scholar] [CrossRef]
- Tian, Y.; Yue, T.; Zhu, L.; Clinton, N. Modeling population density using land cover data. Ecol. Model. 2005, 189, 72–88. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R. Relation between satellite observed visible-near infrared emissions, population, economic activity and electric power consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Tan, M.; Li, X.; Li, S.; Xin, L.; Wang, X.; Li, Q.; Li, W.; Li, Y.; Xiang, W. Modeling population density based on nighttime light images and land use data in China. Appl. Geogr. 2018, 90, 239–247. [Google Scholar] [CrossRef]
- Chen, K.; McAneney, J.; Blong, R.; Leigh, R.; Hunter, L.; Magill, C. Defining area at risk and its effect in catastrophe loss estimation: A dasymetric mapping approach. Appl. Geogr. 2004, 24, 97–117. [Google Scholar] [CrossRef]
- Zoraghein, H.; Leyk, S.; Ruther, M.; Butten, B.P. Exploiting temporal information in parcel data to re fi ne small area population estimates. Comput. Environ. Urban Syst. 2016, 58, 19–28. [Google Scholar] [CrossRef]
- Zoraghein, H.; Leyk, S. Enhancing areal interpolation frameworks through dasymetric refinement to create consistent population estimates across censuses Enhancing areal interpolation frameworks through. Int. J. Geogr. Inf. Sci. 2018, 32, 1948–1976. [Google Scholar] [CrossRef] [PubMed]
- Zoraghein, H.; Leyk, S. Data-enriched interpolation for temporally consistent population compositions. GISci. Remote Sens. 2019, 56, 430–461. [Google Scholar] [CrossRef]
- Zandbergen, P.A.; Ignizio, D.A. Comparison of Dasymetric Mapping Techniques for Small-Area Population Estimates. Cartogr. Geogr. Inf. Sci. 2010, 37, 199–214. [Google Scholar] [CrossRef]
- Balk, D.; Yetman, G. The Global Distribution of Population: Evaluating the Gains in Resolution Refinement; Columbia University Press: New York, NY, USA, 2004; Available online: https://sedac.ciesin.columbia.edu/downloads/docs/gpw-v3/gpw3_documentation_final.pdf (accessed on 8 November 2019).
- Doxsey-Whitfield, E.; Macmanus, K.; Adamo, S.B.; Pistolesi, L.; Squires, J.; Borkovska, O.; Baptista, S.R.; Macmanus, K.; Adamo, S.B.; Pistolesi, L.; et al. Taking Advantage of the Improved Availability of Census Data: A First Look at the Gridded Population of the World, Version 4. Pap. Appl. Geogr. 2015, 1, 226–234. [Google Scholar] [CrossRef]
- Bhaduri, B.; Bright, E.; Coleman, P.; Urban, M.L. LandScan USA: A high-resolution geospatial and temporal modeling approach for population distribution and dynamics. GeoJournal 2007, 69, 103–117. [Google Scholar] [CrossRef]
- Mennis, J. Generating Surface Models of Population Using Dasymetric Mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Ye, T.; Zhao, N.; Yang, X.; Ouyang, Z.; Liu, X.; Chen, Q.; Hu, K.; Yue, W.; Qi, J.; Li, Z.; et al. Science of the Total Environment Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model. Sci. Total Environ. 2019, 658, 936–946. [Google Scholar] [CrossRef]
- Yue, T.X.; Wang, Y.A.; Chen, S.P.; Liu, J.Y.; Qiu, D.S.; Deng, X.Z.; Liu, M.L.; Tian, Y.Z. Numerical simulation of population distribution in China. Popul. Environ. 2003, 25, 141–163. [Google Scholar] [CrossRef]
- Sutton, P.C.; Elvidge, C.; Obremski, T. Building and Evaluating Models to Estimate Ambient Population Density. Photogramm. Eng. Remote Sens. 2003, 69, 545–553. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Stevens, F.R.; Linard, C.; Jia, P.; Tatem, A.J. High Resolution Population Distribution Maps for Southeast Asia in 2010 and 2015. PLoS ONE 2015, 8, e55882. [Google Scholar] [CrossRef] [PubMed]
- Sutton, P.C.; Taylor, M.J.; Elvidge, C.D. Using DMSP OLS Imagery to Characterize Urban Populations in Developed and Developing Countries. In Remote Sensing of Urban and Suburban Areas; Springer: Dordrecht, The Netherlands, 2010; pp. 329–348. [Google Scholar]
- Gallego, F.J. A population density grid of the European Union. Popul. Environ. 2010, 31, 460–473. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Pan, Y.; Ma, Y.; Li, T.; Chen, S. Mapping population distribution by integrating night-time light satellite imagery and land-cover data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2186–2189. [Google Scholar]
- Linard, C.; Gilbert, M.; Snow, R.W.; Noor, A.M.; Tatem, A.J. Population distribution, settlement patterns and accessibility across Africa in 2010. PLoS ONE 2012, 7, e31743. [Google Scholar] [CrossRef]
- Sutton, P.; Roberts, D.; Elvidge, C.; Baugh, K. Census from Heaven: An estimate of the global human population using night-time satellite imagery. Int. J. Remote Sens. 2001, 22, 3061–3076. [Google Scholar] [CrossRef]
- Jing, X.; Shao, X.; Cao, C.; Xiaodong, L.Y. Comparison between the Suomi-NPP Day-Night Band and DMSP-OLS for Correlating Socio-Economic Variables at the Provincial Level in China. Remote Sens. 2016, 8, 17. [Google Scholar] [CrossRef]
- Bagan, H.; Yamagata, Y. Analysis of urban growth and estimating population density using satellite images of nighttime lights and land-use and population data. GISci. Remote Sens. 2015, 52, 765–780. [Google Scholar]
- Small, C.; Pozzi, F.; Elvidge, C.D. Spatial analysis of global urban extent from DMSP-OLS night lights. Remote Sens. Environ. 2005, 96, 277–291. [Google Scholar] [CrossRef]
- Imhoff, M.; Lawrence, W.T.; Elvidge, C.D. A technique for using composite DMSP/OLS “City Lights” satellite data to map urban area. Remote Sens. Environ. 1997, 61, 361–370. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P. A temperature and vegetation adjusted NTL urban index for urban area mapping and analysis. ISPRS J. Photogramm. Remote Sens. 2018, 135, 93–111. [Google Scholar] [CrossRef]
- Miller, S.D.; Turner, R.E. A dynamic lunar spectral irradiance data set for NPOESS/VIIRS day/night band night time environmental applications. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2316–2329. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Hu, Y.; Huang, C.; Shi, K.; Wu, J. Estimating House Vacancy Rate in Metropolitan Areas Using NPP-VIIRS Nighttime Light Composite Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2188–2197. [Google Scholar] [CrossRef]
- Wang, X.; Rafa, M.; Moyer, J.D.; Li, J.; Scheer, J.; Sutton, P. Estimation and Mapping of Sub-National GDP in Uganda Using NPP-VIIRS Imagery. Remote Sens. 2019, 11, 163. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W. A test of the new VIIRS lights data set: Population and economic output in Africa. Remote Sens. 2015, 7, 4937–4947. [Google Scholar] [CrossRef]
- Amaral, S.; Câmara, G.; Monteiro, A.M.V.; Quintanilha, J.A.; Elvidge, C.D. Estimating population and energy consumption in Brazilian Amazonia using DMSP night-time satellite data. Comput. Environ. Urban Syst. 2005, 29, 179–195. [Google Scholar] [CrossRef]
- Dong, N.; Yang, X.; Cai, H.; Wang, L. A novel method for simulating urban population potential based on urban patches: A case study in Jiangsu Province, China. Sustainability 2015, 7, 3984–4003. [Google Scholar] [CrossRef]
- Yu, B.; Lian, T.; Huang, Y.; Yao, S.; Ye, X.; Chen, Z.; Yang, C.; Wu, J. Integration of nighttime light remote sensing images and taxi GPS tracking data for population surface enhancement Bailang. Int. J. Geogr. Inf. Sci. 2019, 33, 687–706. [Google Scholar] [CrossRef]
- Lu, D.; Tian, H.; Zhou, G.; Ge, H. Regional mapping of human settlements in southeastern China with multisensor remotely sensed data. Remote Sens. Environ. 2008, 112, 3668–3679. [Google Scholar] [CrossRef]
- Maithani, P.K.R.C.S. Monitoring Growth of Built-up areas in Indo-Gangetic Plain using Multi-sensor Remote Sensing Data. J. Indian Soc. Remote Sens. 2010, 38, 291–300. [Google Scholar]
- Yu, B.; Tang, M.; Wu, Q.; Yang, C.; Deng, S.; Shi, K.; Peng, C.; Wu, J.; Chen, Z. Urban built-up area extraction from log-transformed NPP-VIIRS nighttime light composite data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1279–1283. [Google Scholar] [CrossRef]
- Guo, W.; Lu, D.; Wu, Y.; Zhang, J. Mapping impervious surface distribution with integration of SNNP VIIRS-DNB and MODIS NDVI Data. Remote Sens. 2015, 7, 12459–12477. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Remote Sensing of Environment Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. Remote Sensing of Environment A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.S.; Gumma, M.K.; Teluguntla, P.; Poehnelt, J.; Congalton, R.G.; Yadav, K.; Thau, D. ISPRS Journal of Photogrammetry and Remote Sensing Automated cropland mapping of continental Africa using Google Earth Engine cloud computing. ISPRS J. Photogramm. Remote Sens. 2017, 126, 225–244. [Google Scholar] [CrossRef]
- Goldblatt, R.; You, W.; Hanson, G.; Khandelwal, A.K. Detecting the Boundaries of Urban Areas in India: A Dataset for Pixel-Based Image Classification in Google Earth Engine. Remote Sens. 2016, 8, 634. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. ISPRS Journal of Photogrammetry and Remote Sensing Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Song, W.; Liu, H.; Wu, Q.; Shi, K.; Wu, J. A New Approach for Detecting Urban Centers and Their Spatial Structure With Nighttime Light Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6305–6319. [Google Scholar] [CrossRef]
- Li, X.; Xu, H.; Chen, X.; Li, C. Potential of NPP-VIIRS nighttime light imagery for modeling the regional economy of China. Remote Sens. 2013, 5, 3057–3081. [Google Scholar] [CrossRef]
- Bhandari, S.; Phinn, S.; Gill, T.; Bhandari, S.; Phinn, S.; Gill, T. Assessing viewing and illumination geometry effects on the MODIS vegetation index (MOD13Q1) time series: Implications for monitoring phenology and disturbances in forest communities in. Int. J. Remote Sens. 2011, 32, 7513–7538. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef] [PubMed]
- Santillan, J.R.; Makinano-santillan, M. Vertical accuracy assessment of 30-m resolution alos, aster, and srtm global dems over northeastern mindanao, philippines. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 149–156. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Yu, L.; Wang, L.; Liu, X.; Shi, T.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM + data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Responses of Suomi-NPP VIIRS-derived nighttime lights to socioeconomic activity in Chinas cities. Remote Sens. Lett. 2014, 5, 165–174. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature – vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q.; Li, G. Residential population estimation using a remote sensing derived impervious surface approach. Int. J. Remote Sens. 2006, 27, 3553–3570. [Google Scholar] [CrossRef]
- Hao, R.; Yu, D.; Sun, Y.; Cao, Q.; Liu, Y.; Liu, Y. Integrating multiple source data to enhance variation and weaken the blooming effect of DMSP-OLS light. Remote Sens. 2015, 7, 1422–1440. [Google Scholar] [CrossRef]
- Heinl, M.; Hammerle, A.; Tappeiner, U.; Leitinger, G. Determinants of urban-rural land surface temperature differences—A landscape scale perspective. Landsc. Urban Plan. 2015, 134, 33–42. [Google Scholar] [CrossRef]
- Du, Y.; Xie, Z.; Zeng, Y.; Shi, Y.; Wu, J. Impact of urban expansion on regional tempera- ture change in the Yangtze River Delta. J. Geogr. Sci. 2007, 17, 387–389. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Remote Sensing of Environment Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Price, J.C. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens. 1990, 28, 940–948. [Google Scholar] [CrossRef] [Green Version]
- Yue, W.; Xu, J.; Tan, W.; Xu, L. The relationship between land surface temperature and NDVI with remote sensing: Application to Shanghai Landsat 7 ETM + data. Int. J. Remote Sens. 2007, 28, 3205–3226. [Google Scholar] [CrossRef]
- Lambin, E.F.; Ehrlich, D. Land-cover Changes in Sub-Saharan Africa (1982–1991): Application of a Change Index Based on Remotely Sensed Surface Temperature and Vegetation Indices at a Continental Scale. Remote Sens. Environ. 1997, 61, 181–200. [Google Scholar] [CrossRef]
- Melesse, A.M.; Jordan, J.D. Spatially distributed watershed mapping and modeling: Thermal maps and vegetation indices to enhance land cover and surface microclimate mapping: Part 1. J. Spat. Hydrol. 2003, 3, 1–29. [Google Scholar]
- Lambin, E.F.; Ehrlich, D. Combining vegetation indices and surface temperature for land-cover mapping at broad spatial scales. Int. J. Remote Sens. 1995, 16, 573–579. [Google Scholar] [CrossRef]
- Lambin, E.F.; Ehrlich, D. The surface temperature-vegetation index space for land cover and land-cover change analysis. Int. J. Remote Sens. 1996, 17, 463–487. [Google Scholar] [CrossRef]
- Small, C.; Elvidge, C.D.; Baugh, K. Mapping Urban Structure and Spatial Connectivity with VIIRS and OLS Night Light Imagery. In Proceedings of the Joint Urban Remote Sensing Event 2013, São Paulo, Brazil, 21–23 April 2013; IEEE; pp. 230–233. [Google Scholar]
- Dong, P.; Ramesh, S.; Nepali, A. Evaluation of small-area population estimation using LiDAR, Landsat TM and parcel data. Int. J. Remote Sens. 2010, 31, 5571–5586. [Google Scholar] [CrossRef]
- Gao, B.; Huang, Q.; He, C.; Ma, Q. Dynamics of Urbanization Levels in China from 1992 to 2012: Perspective from DMSP/OLS Nighttime Light Data. Remote Sens. 2015, 7, 1721–1735. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Smith, S.J.; Elvidge, C.D.; Zhao, K.; Thomson, A.; Imhoff, M. A cluster-based method to map urban area from DMSP/OLS nightlights. Remote Sens. Environ. 2014, 147, 173–185. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-Sensed and Ancillary Data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef]
- Gaughan, A.E.; Stevens, F.R.; Huang, Z.; Nieves, J.J.; Sorichetta, A.; Lai, S.; Ye, X.; Linard, C.; Hornby, G.M.; Hay, S.I.; et al. Spatiotemporal patterns of population in mainland China, 1990 to 2010. Sci. DATA 2016, 3, 160005. [Google Scholar] [CrossRef] [PubMed]










| Region | Selected Regression Model | F | P Value | RMSE | MRE | MdRE | |
|---|---|---|---|---|---|---|---|
| A | PD=−9E06 + 46122 VTLPI + 1.2 | 0.81 | 60.30 | 0.00 | 206.46 | 0.26 | 0.19 |
| B | PD = 10170 + 10371VTLPI − 7.3 | 0.98 | 4231.63 | 0.00 |
| Variables | Best Regression Model | RMSE | MRE | MdRE | |
|---|---|---|---|---|---|
| VTLPI | PD_a=-9E06+46122VTLPI+1.2 | 0.807 | 206.46 | 0.26 | 0.19 |
| PD_b=10170+ 10371VTLPI – 7.3 | 0.983 | ||||
| HSI | PD_a=-121943+8166HSI-10.7 | 0.705 | 358.74 | 0.47 | 0.38 |
| PD_b=529492+1725HSI-347.2 | 0.964 | ||||
| DNB | PD_a=-1E102+1E06DNB+3.9 | 0.746 | 262.14 | 0.49 | 0.28 |
| PD_b=672082+64554DNB+289 | 0.937 |
| Population Data Products | RMSE | MAE | MdRE |
|---|---|---|---|
| VTLPI- based | 212.31 | 0.29 | 0.12 |
| DNB- based | 231.99 | 0.36 | 0.25 |
| HSI- based | 352.00 | 0.64 | 0.39 |
| LandScan | 348.05 | 0.50 | 0.44 |
| WorldPop | 312.34 | 0.42 | 0.38 |
| GPW | 329.92 | 0.41 | 0.26 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, P.; Zhang, X.; Cheng, J.; Sun, Q. Modeling Population Density Using a New Index Derived from Multi-Sensor Image Data. Remote Sens. 2019, 11, 2620. https://doi.org/10.3390/rs11222620
Luo P, Zhang X, Cheng J, Sun Q. Modeling Population Density Using a New Index Derived from Multi-Sensor Image Data. Remote Sensing. 2019; 11(22):2620. https://doi.org/10.3390/rs11222620
Chicago/Turabian StyleLuo, Peng, Xianfeng Zhang, Junyi Cheng, and Quan Sun. 2019. "Modeling Population Density Using a New Index Derived from Multi-Sensor Image Data" Remote Sensing 11, no. 22: 2620. https://doi.org/10.3390/rs11222620
APA StyleLuo, P., Zhang, X., Cheng, J., & Sun, Q. (2019). Modeling Population Density Using a New Index Derived from Multi-Sensor Image Data. Remote Sensing, 11(22), 2620. https://doi.org/10.3390/rs11222620