Purifying SLIC Superpixels to Optimize Superpixel-Based Classification of High Spatial Resolution Remote Sensing Image
Abstract
:1. Introduction
2. Background and Methods
2.1. Simple Linear Iterative Clustering (SLIC) Superpixels
- (1)
- For each cluster center, calculate the distance D between the cluster center and pixels within the search space centered by the cluster center and assign each pixel to the nearest cluster center.
- (2)
- Update new cluster centers by calculating the mean vector of all the pixels belonging to the superpixel.
- (3)
- Calculate the residual error E, which is the distance between previous center locations and updated center locations.
2.2. SLIC Superpixels Purification Algorithm Based on Color Quantization
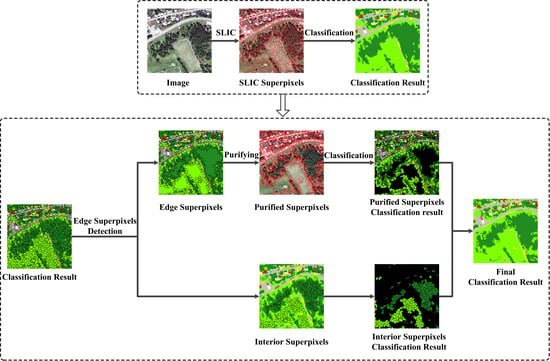
2.3. High Spatial Resolution Remote Sensing Image Classification Based on Purified SLIC Superpixels
3. Datasets and Experimental Results
3.1. Datasets
3.2. Segmentation Quality Comparison between Purified SLIC Superpixels and Original SLIC Superpixels
3.3. Comparison of Remote Sensing Image Classification Results Generated from Purified SLIC Superpixels and Original SLIC Superpixels
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Csillik, O. Fast Segmentation and Classification of Very High Resolution Remote Sensing Data Using SLIC Superpixels. Remote Sens. 2017, 9, 243. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less is more: Optimizing classification performance through feature selection in a very-high-resolution remote sensing object-based urban application. GIScience Remote Sens. 2018, 55, 221–242. [Google Scholar] [CrossRef]
- Han, W.; Feng, R.; Wang, L.; Cheng, Y. A semi-supervised generative framework with deep learning features for high-resolution remote sensing image scene classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 23–43. [Google Scholar]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Meer, F.V.D.; Werff, H.V.D.; Coillie, F.V. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Hay, G.J.; Castilla, G. Geographic Object-Based Image Analysis (GEOBIA): A new name for a new discipline. In Object-Based Image Analysis; Springer: Berlin/Heidelberg, Germany, 2008; pp. 75–89. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [Green Version]
- Cheng, J.; Bo, Y.; Zhu, Y.; Ji, X. A novel method for assessing the segmentation quality of high-spatial resolution remote-sensing images. Int. J. Remote Sens. 2014, 35, 3816–3839. [Google Scholar] [CrossRef]
- Arvor, D.; Durieux, L.; Andrés, S.; Laporte, M.A. Advances in geographic object-based image analysis with ontologies: A review of main contributions and limitations from a remote sensing perspective. ISPRS J. Photogramm. Remote Sens. 2013, 82, 125–137. [Google Scholar] [CrossRef]
- Drăguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Baatz, M.; Schäpe, A. An optimization approach for high quality multi-scale image segmentation. Angew. Geogr. Inf. Sverarbeitung 2000, 12, 12–23. [Google Scholar]
- Tong, H.; Maxwell, T.; Zhang, Y.; Dey, V. A supervised and fuzzy-based approach to determine optimal multi-resolution image segmentation parameters. Photogramm. Eng. Remote Sens. 2012, 78, 1029–1044. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Jia, X.; Hu, J. Superpixel-based graphical model for remote sensing image mapping. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5861–5871. [Google Scholar] [CrossRef]
- Ren, X.; Malik, J. Learning a classification model for segmentation. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 14–17 October 2003; Volume 1, pp. 10–17. [Google Scholar]
- Neubert, P.; Protzel, P. Superpixel benchmark and comparison. In Proceedings of the Forum Bildverarbeitung 2012, Regensburg, Germany, 29–30 November 2012; Volume 6. [Google Scholar]
- Li, Z.; Chen, J. Superpixel segmentation using linear spectral clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1356–1363. [Google Scholar]
- Shi, C.; Wang, L. Incorporating spatial information in spectral unmixing: A review. Remote Sens. Environ. 2014, 149, 70–87. [Google Scholar] [CrossRef]
- Fourie, C.; Schoepfer, E. Data transformation functions for expanded search spaces in geographic sample supervised segment generation. Remote Sens. 2014, 6, 3791–3821. [Google Scholar] [CrossRef]
- Ma, L.; Du, B.; Chen, H.; Soomro, N.Q. Region-of-interest detection via superpixel-to-pixel saliency analysis for remote sensing image. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1752–1756. [Google Scholar] [CrossRef]
- Arisoy, S.; Kayabol, K. Mixture-based superpixel segmentation and classification of SAR images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1721–1725. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, X.; Li, J.; Plaza, A.; Prasad, S. Superpixel-based active learning and online feature importance learning for hyperspectral image analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 347–359. [Google Scholar] [CrossRef]
- Tong, F.; Tong, H.; Jiang, J.; Zhang, Y. Multiscale union regions adaptive sparse representation for hyperspectral image classification. Remote Sens. 2017, 9, 872. [Google Scholar] [CrossRef]
- Li, S.; Lu, T.; Fang, L.; Jia, X.; Benediktsson, J.A. Probabilistic fusion of pixel-level and superpixel-level hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7416–7430. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A Superpixelwise PCA Approach for Unsupervised Feature Extraction of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Ma, J.; Wang, Z.; Chen, C.; Liu, X. Hyperspectral Image Classification in the Presence of Noisy Labels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 851–865. [Google Scholar] [CrossRef]
- Ortiz Toro, C.; Gonzalo Martín, C.; García Pedrero, Á.; Menasalvas Ruiz, E. Superpixel-based roughness measure for multispectral satellite image segmentation. Remote Sens. 2015, 7, 14620–14645. [Google Scholar] [CrossRef]
- Vargas, J.E.; Falcão, A.X.; Dos Santos, J.; Esquerdo, J.C.D.M.; Coutinho, A.C.; Antunes, J. Contextual superpixel description for remote sensing image classification. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1132–1135. [Google Scholar]
- Garcia-Pedrero, A.; Gonzalo-Martin, C.; Fonseca-Luengo, D.; Lillo-Saavedra, M. A GEOBIA methodology for fragmented agricultural landscapes. Remote Sens. 2015, 7, 767–787. [Google Scholar] [CrossRef]
- Stefanski, J.; Mack, B.; Waske, B. Optimization of object-based image analysis with random forests for land cover mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2492–2504. [Google Scholar] [CrossRef]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vis. Image Underst. 2018, 166, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Conrad, C.; Mertz, M.; Mester, R. Contour-Relaxed Superpixels. In Energy Minimization Methods in Computer Vision and Pattern Recognition; Heyden, A., Kahl, F., Olsson, C., Oskarsson, M., Tai, X.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 280–293. [Google Scholar]
- Buyssens, P.; Gardin, I.; Ruan, S. Eikonal based region growing for superpixels generation: Application to semi-supervised real time organ segmentation in CT images. Innovat. Res. BioMed. Eng. 2014, 35, 20–26. [Google Scholar] [CrossRef] [Green Version]
- Van den Bergh, M.; Boix, X.; Roig, G.; Van Gool, L. SEEDS: Superpixels Extracted Via Energy-Driven Sampling. Int. J. Comput. Vis. 2015, 111, 298–314. [Google Scholar] [CrossRef]
- Yao, J.; Boben, M.; Fidler, S.; Urtasun, R. Real-Time Coarse-to-Fine Topologically Preserving Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Wu, X. Color quantization by dynamic programming and principal analysis. ACM Trans. Graph. 1992, 11, 348–372. [Google Scholar] [CrossRef]
- Connolly, C.; Fleiss, T. A study of efficiency and accuracy in the transformation from RGB to CIELAB color space. IEEE Trans. Image Process. 1997, 6, 1046–1048. [Google Scholar] [CrossRef] [PubMed]
- Braquelaire, J.P.; Brun, L. Comparison and optimization of methods of color image quantization. IEEE Trans. Image Process. 1997, 6, 1048–1052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- K8, S. A Simple—Yet Quite Powerful—Palette Quantizer in C#. Available online: https://www.codeproject.com/Articles/66341/A-Simple-Yet-Quite-Powerful-Palette-Quantizer-in-C (accessed on 25 April 2019).
- Luo, M.R.; Cui, G.H.; Rigg, B. The development of the CIE 2000 colour-difference formula: CIEDE2000. Color Res. Appl. 2001, 26, 340–350. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef] [PubMed]
- Alex, L.; Adrian, S.; Kutulakos, K.N.; Fleet, D.J.; Dickinson, S.J.; Kaleem, S. TurboPixels: Fast superpixels using geometric flows. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2290–2297. [Google Scholar]
- Moore, A.P.; Prince, S.J.; Warrell, J.; Mohammed, U.; Jones, G. Superpixel lattices. In Proceedings of the 2008 IEEE conference on computer vision and pattern recognition, Anchorage, AK, USA, 24–26 June 2008; Citeseer: Pittsburgh, PA, USA, 2008; pp. 1–8. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef] [Green Version]












| Image 24,063 | Image 29,030 | Image 201,080 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Rec | UE | EV | Rec | UE | EV | Rec | UE | EV | |
| SLIC | 0.8347 | 0.0466 | 0.9736 | 0.8261 | 0.0600 | 0.9170 | 0.8753 | 0.0514 | 0.9268 |
| Purified SLIC | 0.8727 | 0.0360 | 0.9865 | 0.8622 | 0.0434 | 0.9453 | 0.9150 | 0.0328 | 0.9583 |
| SLIC | 0.7743 | 0.0641 | 0.9620 | 0.7840 | 0.0847 | 0.8821 | 0.8391 | 0.0728 | 0.9049 |
| Purified SLIC | 0.8338 | 0.0435 | 0.9834 | 0.8208 | 0.0579 | 0.9342 | 0.9030 | 0.0406 | 0.9507 |
| SLIC | 0.7630 | 0.0776 | 0.9540 | 0.5790 | 0.1051 | 0.8737 | 0.7328 | 0.0937 | 0.8859 |
| Purified SLIC | 0.8202 | 0.0527 | 0.9787 | 0.6523 | 0.0706 | 0.9308 | 0.7883 | 0.0479 | 0.9422 |
| Tree | 40,621 | 15,555 | 7457 |
| Light Roof | 564 | 189 | 90 |
| Road | 8394 | 3271 | 1614 |
| Grass | 16,651 | 6108 | 2879 |
| Dark Roof | 2069 | 715 | 374 |
| Bare Soil | 4212 | 1483 | 677 |
| Water | 4654 | 1919 | 998 |
| Total | 77,165 | 29,240 | 14,089 |
| SLIC superpixels | 205,700 | 87,442 | 46,778 |
| OA(%) | AA(%) | Kappa | |
|---|---|---|---|
| SLIC | 77.74 | 67.97 | 0.697 |
| Purified SLIC | 79.68 | 71.29 | 0.725 |
| All Purified SLIC | 79.51 | 71.26 | 0.722 |
| SLIC | 75.99 | 65.15 | 0.674 |
| Purified SLIC | 79.41 | 70.83 | 0.722 |
| All Purified SLIC | 79.20 | 70.80 | 0.720 |
| SLIC | 74.12 | 62.80 | 0.648 |
| Purified SLIC | 78.80 | 70.46 | 0.714 |
| All Purified SLIC | 78.62 | 70.42 | 0.712 |
| SLIC | Purified SLIC | SLIC | Purified SLIC | SLIC | Purified SLIC | |
|---|---|---|---|---|---|---|
| SLIC | 27 | 27 | 23 | 23 | 22 | 22 |
| Feature Extraction | 5230 | 5230 | 2177 | 2177 | 1174 | 1174 |
| RF Training | 212 | 212 | 74 | 74 | 33 | 33 |
| Classification | 30 | 30 | 11 | 11 | 5 | 5 |
| Purifying | – | 110 | – | 93 | – | 92 |
| Feature Extraction | – | 2584 | – | 2155 | – | 1752 |
| Classification | – | 17 | – | 12 | – | 8 |
| Total | 5499 | 8210 | 2285 | 4545 | 1234 | 3086 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, H.; Tong, F.; Zhou, W.; Zhang, Y. Purifying SLIC Superpixels to Optimize Superpixel-Based Classification of High Spatial Resolution Remote Sensing Image. Remote Sens. 2019, 11, 2627. https://doi.org/10.3390/rs11222627
Tong H, Tong F, Zhou W, Zhang Y. Purifying SLIC Superpixels to Optimize Superpixel-Based Classification of High Spatial Resolution Remote Sensing Image. Remote Sensing. 2019; 11(22):2627. https://doi.org/10.3390/rs11222627
Chicago/Turabian StyleTong, Hengjian, Fei Tong, Wei Zhou, and Yun Zhang. 2019. "Purifying SLIC Superpixels to Optimize Superpixel-Based Classification of High Spatial Resolution Remote Sensing Image" Remote Sensing 11, no. 22: 2627. https://doi.org/10.3390/rs11222627
APA StyleTong, H., Tong, F., Zhou, W., & Zhang, Y. (2019). Purifying SLIC Superpixels to Optimize Superpixel-Based Classification of High Spatial Resolution Remote Sensing Image. Remote Sensing, 11(22), 2627. https://doi.org/10.3390/rs11222627