The Influence of Heterogeneity on Lunar Irradiance Based on Multiscale Analysis

Abstract

The Moon is a stable light source for the radiometric calibration of satellite sensors. It acts as a diffuse panel that reflects sunlight in all directions, however, the lunar surface is heterogeneous due to its topography and different mineral content and chemical composition at different locations, resulting in different optical properties. In order to perform radiometric calibration using the Moon, a lunar irradiance model using different observation geometry is required. Currently, two lunar irradiance models exist, namely, the Robotic Lunar Observatory (ROLO) and the Miller and Turner 2009 (MT2009). The ROLO lunar irradiance model is widely used as the radiometric standard for on-orbit sensors. The MT2009 lunar irradiance model is popular for remote sensing at night, however, the original version of the MT2009 lunar irradiance model takes less consideration of the heterogeneous lunar surface and lunar topography. Since the heterogeneity embedded in the lunar surface is the key to the improvement of the lunar irradiance model, this study analyzes the influence of the heterogeneous surface on the irradiance of moonlight based on model data at different scales. A heterogeneous correction factor is defined to describe the impact of the heterogeneous lunar surface on lunar irradiance. On the basis of the analysis, the following conclusions can be made. First, the influence of heterogeneity in the waning hemisphere is greater than that in waxing hemisphere under all 32 wavelengths of the ROLO filters. Second, the influence of heterogeneity embedded in the lunar surface exerts less impact on lunar irradiance at lower resolution. Third, the heterogeneous correction factor is scale independent. Finally, the lunar irradiance uncertainty introduced by topography is very small and decreases as the resolution of model data decreases due to the loss of topographic information.

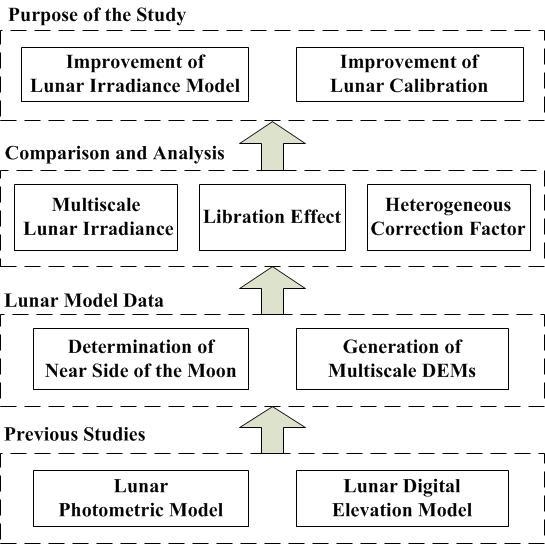
1. Introduction

Due to its photometric stability, radiometric calibration using the Moon as a standard light source, also known as lunar calibration, has been widely used by on-orbit sensors, such as Moderate Resolution Imaging Spectroradiometer (MODIS), Sea-Viewing Wide Field-of-View Sensor (SeaWiFS), Visible Infrared Imager Radiometer Suite (VIIRS), Landsat Multispectral Scanner (MSS), and Geostationary Operational Environmental Satellite (GOES) visible imager [1,2,3,4,5,6]. In order to perform lunar calibration, empirical models describing lunar irradiance under different observation geometries are required. Two lunar irradiance models, namely, the Robotic Lunar Observatory (ROLO) and the Miller and Turner 2009 (MT2009), have been developed. The ROLO model describes the irradiance of moonlight under different lunar phases and librations, and its absolute scale is derived from the spectra of the star Vega and returned Apollo samples [7]. Currently, it is considered to be the best lunar radiometric reference and numerous efforts have been made to make the model an absolute reference for lunar calibration [8]. Brown et al. (2017) [9] developed an approach by establishment an absolute top-of-atmosphere (TOA) lunar irradiance model and demonstrated the ability to make the output of the ROLO model at a phase angle of seven degrees absolutely SI-traceable to the TOA lunar irradiance measured at Mt. Hopkins at a phase angle of 6.6 degrees. The MT2009 lunar irradiance model accounts for the variation of the lunar phase, however, it takes less consideration of lunar topography, surface heterogeneity, and the libration effect [10]. Both models have been widely used in applications including lunar calibration, night-time aerosol retrieval, and in socioeconomic fields [11,12,13,14,15].

Since the lunar surface is heterogeneous both in its composition and terrain types, one difficulty of establishing a lunar irradiance model is the consideration of its global heterogeneity. In addition, on-orbit sensors are built with different resolutions. Therefore, the impact of heterogeneity at different resolutions on the irradiance of the moonlight is a topic of interest. Many studies on surface roughness based on multiscale analysis have been conducted. Hani et al. (2011) [16] proposed an innovative method to compute surface roughness based on multiscale analysis. The proposed method could discriminate between convex and concave regions, and shallow and deep incisions, at different scales. Rosenburg et al. (2011) [17] calculated the Hurst exponent, the root mean square (RMS) slopes and median slopes to measure the roughness of the lunar surface. The results showed that lunar highland and maria plains exhibited different roughness properties. Kreslavsky et al. (2013) [18] analyzed the geomorphological and geological information of the lunar surface based on the hectometer-scale and kilometer-scale roughness. Cao et al. (2015) [19] used a structure element (SE) to measure the roughness of lunar surface. On the basis of the lunar orbital laser altimeter (LOLA) data, global roughness maps with different resolutions were created to interpret the stability of the roughness measure. Although abundant studies of surface roughness using multiscale analysis have been performed, the impact of the heterogeneous lunar surface at different scales on the irradiance of moonlight is less studied. The key to studying this issue is a function predicting the texture of the lunar surface under different illumination and viewing angles. Previous studies have paved the way to solving the problem. Yokota et al. (2011) [20] divided the lunar surface into three groups, and a photometric model was created for each group using Selenological and Engineering Explorer (SELENE) Spectral Profiler (SP) data. The texture function of the lunar surface under different illumination and viewing angles at 1° × 1° resolution meshes was created. Similarly, Wu et al. (2013) [21] divided the lunar surface into four categories based on the percentage of FeO content. The photometric model of each category was created and used to remove the geometric effect. The results showed that corrected reflectance in two adjacent orbits displayed better consistency than the uncorrected reflectance. Kieffer and Stone (2009) [7] extensively studied the radiometric property of 11 selected lunar regions. These areas (chips) are globally distributed on the lunar surface. The chips are 3 × 3 pixel squares in a modified Lambert azimuth equal area projection of the ROLO images. Buratti et al. (2011) [22] fitted a fourth-order polynomial with an extra exponential term to 36,000 photometric data points from the 11 ROLO focus regions at each of the 32 wavelengths of the ROLO filters and derived the photometric model of two lunar terrain types, namely, maria and highland, based on the Lommel–Seeliger function. Hicks et al. (2011) [23] derived photometric models of “maria” and ”not maria” terrains based on Moon Mineralogy Mapper (M³) data. The models agree well with the models derived in [22], however, the effective solar phase angle interval is between 24 and 90 degrees.

Previous results showed that the derived night-time top-of-atmosphere (TOA) reflectance using the MT2009 lunar irradiance model had a strong lunar phase dependency [24,25]. The dependency is due to the heterogeneous lunar surface, which is less considered by the original version of the MT2009 lunar irradiance model [10]. In this study, we evaluate the influence of the lunar surface on lunar irradiance and simulate it at eight different scales. Since ROLO is currently the best lunar radiometric reference [8], photometric models of the two typical terrain types of the lunar surface based on ROLO lunar observation datasets are selected to describe the reflectance of each point on the lunar surface. The LOLA data are combined to determine the impact of lunar topography considering the solar phase, illumination, and viewing angles. An algorithm is developed to determine the near side of the lunar surface visible to the observers, allowing a model of the lunar near side under different lunar phases and librations to be created. A correction factor is defined to measure the impact of heterogeneity on the irradiance of the moonlight. The factor, under different lunar phases, is also calculated. The influence by heterogeneity on lunar irradiance is analyzed based on the correction factor at eight different scales. The result shows that the heterogeneous correction factor is scale independent, indicating the ability to measure the degree of impact due to heterogeneity upon lunar irradiance at varying scales. The heterogeneous correction factors at all 32 wavelengths of the ROLO filters follow the same trend with greater values during the waxing lunar phases than during the waning lunar phases. The correction factor approaches one as the resolution decreases, indicating less impact of heterogeneity on lunar irradiance at lower resolutions. The lunar irradiance uncertainty introduced by the topography is small and decreases as the resolution of simulated lunar images decreases due to the loss of topographic information. The results of this study are meaningful to the improvement of the lunar irradiance model and its application in nocturnal remote sensing.

2. Methodology

In this study, the global topography of the lunar surface is determined using LOLA data. To study the impact of heterogeneity on lunar irradiance, model data at different scales are generated. The overall methodology is as follows: generation of multiscale digital elevation models (DEMs), generation of multiscale lunar irradiance dataset, comparison of lunar irradiance at different scales, evaluation of the libration effect and, finally, evaluation of the heterogeneous correction factor at different scales. The details of the analysis method are described below.

2.1. Generation of Multiscale DEMs

The LOLA data provided the global topography of the lunar surface with a resolution of 256 pixels per degree. In this study, the multiscale global topography was derived from LOLA data with a resolution of 8 pixels per degree, 4 pixels per degree, 2 pixels per degree, 1 pixel per degree, 0.5 pixels per degree, 0.25 pixels per degree, 0.1 pixels per degree, and 0.083 pixels per degree. The down sampling of LOLA data was implemented in global maps in a series of square neighborhoods, whose lengths of sides were 32, 64, 128, 256, 512, 1024, 2560, and 3072 pixels. Therefore, the corresponding sizes of the generated grids of the DEMs were 2880 × 1440, 1440 × 720, 720 × 360, 360 × 180, 180 × 90, 90 × 45, 36 × 18, and 30 × 15, respectively. The newly generated DEMs were the averages of each square neighborhood under the assumption that digital elevation data at a given resolution can be interpreted as averages over an area surrounding the point at which the elevation is reported [26]. The generated multiscale DEMs are shown in Figure 1.

As shown in Figure 1, on the one hand, the textures of images in Figure 1a,b show no obvious differences by visual inspection. On the other hand, the details of textures of images in Figure 1c,d are not as clear as in images in Figure 1a,b. As the length of the square neighborhood grows in the images of Figure 1e,f, more details of textures are lost. Finally, the textures in images Figure 1g,h can barely be seen because most details are lost. The Tycho Crater located at 43.31°S, 11.36°W is chosen to examine the detail of the near side of the lunar DEMs at various resolutions. We only provide the DEMs at six resolutions in Figure 2 since the feature is lost in the final two resolutions. Nonetheless, we can see that the images in Figure 2a,b show no obvious difference by visual inspection. The textures in images in Figure 2c–f are less clear as compared to the images in Figure 2a,b.

In order to quantify the details of textures of the DEMs at different scales in Figure 1, the entropy of each digital elevation model (DEM) map at different scales is calculated using Equation (1) [27]:

$$e=-{\displaystyle \sum }_{i=0}^{L-1}p\left(z_i\right)lo{g}_{2}p\left(z_i\right)$$

(1)

where z is a random variable denoting the gray levels of the DEM, L is the number of gray levels, and p(z_i) is the frequency of each gray level. The greater the variation of DEM, the larger the value of entropy. If the DEM values are the same over the global lunar surface, entropy will be zero.

The entropy of the DEMs at eight different scales are given in

Table 1. Entropy of global DEMs at different scale levels.

Scale Level	8 pixels/degree	4 pixels/degree	2 pixels/degree	1 pixel/degree
Entropy	16,977.78	4272.33	1087.52	285.41
Scale level	0.5 pixels/degree	0.25 pixels/degree	0.1 pixels/degree	0.083 pixels/degree
Entropy	81.65	28.43	11.25	10.44

, which shows that the value of entropy gradually decreases from 16,977.78 at a scale of 8 pixels/degree to 10.44 at a scale of 0.083 pixels/degree. By establishing a threshold for the global entropy map, the lunar surface can be divided into two typical terrain types, namely, maria and highland [28].

Using the multiscale DEMs, the global slopes of the lunar surface, at different scales, are derived using a 3 × 3 pixel window. The values of the slope at the eight scales are 6.8303 ± 6.6261, 5.0753 ± 4.8172, 3.3870 ± 3.0873, 1.9619 ± 1.7172, 0.9616 ± 0.9309, 0.5102 ± 0.4517, 0.2574 ± 0.2244, and 0.2037 ± 0.2178, respectively, as shown in Figure 3. It can be seen that the average and standard deviation of the slope decreases as the grid length increases, which is consistent with the results in [29,30]. In this study, the left and right side of the Moon is defined as the waning and waxing hemisphere, respectively. The variation of topography in the waning hemisphere is greater than that in the waxing hemisphere, as deduced from the entropy measurement shown in

Table 2. Entropy of the global DEMs at different scale levels.

	Waning Hemisphere		Waxing Hemisphere
Scale Level	256 pixels/degree	8 pixels/degree	256 pixels/degree	8 pixels/degree
Entropy	5,239,252.83	5130.96	5,124,114.39	5024.82

. Combining the results shown in Figure 1 and Figure 3, Table 1 and Table 2, we can see that the variation of the topography of the lunar surface decreases as the resolution decreases due to the loss of topographic information, and that the variation of the topography of the waning hemisphere is larger than that of the waxing hemisphere.

2.2. The Photometric Model

In order to simulate the irradiance of the Moon, the intensity of one point on the lunar surface at different observation geometries must be known. This can be derived using a photometric model of the lunar surface. Then, the irradiance of the whole lunar surface can be derived by integrating all the points on the lunar surface. As a low-albedo object, it has long been recognized that the lunar surface exhibits a reflectance property that is dominated by singly scattered light [22], which can be described based on the Lommel–Seeliger photometric model. The equation of the model is the following:

$$\frac{I}{F}=f\left(\alpha \right)\left(\frac{{\mu }_0}{{\mu }_1+{\mu }_0}\right)$$

(2)

where I represent the intensity of reflected sunlight (unit W/Sr), F represents the incident solar irradiance, μ₀ represents the cosine of incident angle, μ₁ represents the cosine of reflected angle, and f(α) represents the solar phase function.

The equation of the surface solar phase function is the following:

$$f\left(\alpha \right)=C_0{e}_1^{-C\alpha }+A_0+A_1\alpha +A_2{\alpha }^2+A_3{\alpha }^3+A_4{\alpha }^4$$

(3)

The exponential term in the equation is used to describe the opposition surge at a small surface solar phase angle, expressed in degrees, and the fourth-order polynomial term describes the intensity with the change of surface phase angles. The coefficients of the solar phase function for highland and maria are obtained based on the 11 reference regions defined by Kieffer and Stone using 36,000 photometric data points from the ROLO observations [22]. The photometric model in the above form has also been used in [21,23,31].

The cosines of the incident angle μ₀ and reflected angle μ₁ on the inclined lunar surface are derived using the following two equations:

$${\mu }_0=\cos \left({\theta }_{sz}\right)\cos \left({\theta }_{slope}\right)+\sin \left({\theta }_{sz}\right)\sin \left({\theta }_{slope}\right)\cos \left({\phi }_{aspect}-{\phi }_{saz}\right)$$

(4)

$${\mu }_1=\cos \left({\theta }_{vz}\right)\cos \left({\theta }_{slope}\right)+\sin \left({\theta }_{vz}\right)\sin \left({\theta }_{slope}\right)\cos \left({\phi }_{aspect}-{\phi }_{vaz}\right)$$

(5)

where ${\theta }_{sz}$ indicates the solar zenith angle on a flat surface, ${\phi }_{saz}$ denotes the solar azimuth angle, ${\theta }_{vz}$ represents the viewing zenith angle on a flat surface, ${\phi }_{vaz}$ represents the viewing azimuth angle, ${\theta }_{slope}$ represents the slope of the inclined lunar surface, and ${\phi }_{aspect}$ represents the azimuth of the inclined surface.

With the knowledge of incident solar irradiance and the photometric model of the lunar surface, the intensity of reflected sunlight can be determined. The intensity can be converted into irradiance using the following equation:

$$I\left(\alpha \right)={\displaystyle \sum }_{i=1}^n\frac{L_i}{S_i}·{\Omega }_i$$

(6)

where L_i indicates the intensity of moonlight, Ω_i denotes the solid angle, S_i denotes the area of one point on the lunar surface, and I represent the irradiance of the moonlight at lunar phase angle α.

2.3. Generation of Multiscale Lunar Images

The side of the Moon facing the observer is determined by its position in a Moon-centered coordinate system. The lunar image is a projection of the Moon onto an imaging plane, which is determined by the view orientation of the imager [32]. In order to simplify the imaging process and focus on the radiometric property of the Moon, in this study we assume the imager is located at the center of the Earth and points directly at the center of the Moon. The sub-Earth point on the near side of the lunar surface is not fixed at (0°N, 0°W) in the Moon-centered coordinate system. The apparent motion ranges from −7.6 to 7.6 degrees in longitude and −6.7 to 6.7 degrees in latitude, which is known as the libration effect. The lunar surface looks the same to the naked eye every night, however, it actually changes cyclically with nearly 59% of the lunar surface visible from the Earth. In order to take the libration effect into account in the simulation of lunar irradiance data, the near side of the Moon needs to be known using knowledge of the sub-Earth point on the lunar surface. The following procedures are used to determine the near side of the Moon:

• The sub-Earth point is determined with knowledge of the Julian date using Spacecraft, Planet, Instruments, C-matrix, and Events (SPICE) toolkit.
• The latitude and longitude in moon-centered coordinates, with (−90°, 90°) longitude and (−90°, 90°) latitude is converted into a rectangular coordinate system.
• The rotation matrix is determined using Rodrigues’ rotation formula as follows:

  $$R=Ecos\left(\theta \right)+\left(1-\cos \left(\theta \right)\right)\left[\begin{array}{c}{k}_x\\ k_y\\ k_z\end{array}\right]\left[\begin{array}{ccc}{k}_x& k_y& k_z\end{array}\right]+\sin \left(\theta \right)\left[\begin{array}{ccc}0& k_z& k_y\\ k_z& 0& -k_x\\ -k_y& k_x& 0\end{array}\right]$$

  (7)

  where $\theta$ represents the angle between the unit normal vector at (0°N, 0°W) in the moon-centered coordinate system ($\overrightarrow{n_0}$) and the unit normal vector at sub-Earth point ($\overrightarrow{n_e}$), E represents the three-order unit matrix, and [k_x, k_y, k_z]’ represents the unit vector of rotation axis, which is determined by the cross product of $\overrightarrow{n_0}$ and $\overrightarrow{n_e}$.
  The rectangular coordinates after rotation are derived using the following equation:

  $$\overrightarrow{v_{rot}}=R\overrightarrow{v}$$

  (8)

  where $\overrightarrow{v}$ represents the original points of the rectangular coordinate system and $\overrightarrow{v_{rot}}$ indicates the points after rotation.
• The rectangular coordinates are converted back into latitude and longitude in the moon-centered coordinate system.

Since the viewing point stands at the center of the Earth and points to the center of the Moon, the coordinates projected onto the imaging plane can be derived using the following equations:

$$x=\cos \left(b\right)\sin \left(l\right)$$

(9)

$$y=\sin \left(b\right)$$

(10)

where b and l represent the latitude and longitude of points on the lunar surface, respectively.

The multiscale lunar images are shown in Figure 4. The unit of each point is W/m². The lunar phase of Figure 4a–h are −60 degrees. It can be seen that the topography and heterogeneous surface have been modeled in the image at the scale of 8 pixels/degree in Figure 4a. Here craters including Copernicus (10°N, 20°W), Plato (51.62°N, 9.38°W), and Eratosthenes (14.5°N, 11.3°W), and mountains including Apennine (19.87°N, 0.03°W) and the Alps (48.37°N, 0.58°W), are shown separately to validate the model data shown in Figure 4a. The resolution of Figure 4h is the lowest among all the images in Figure 4 and corresponds to the resolution of lunar images captured by sensors such as SeaWiFS and MODIS at 1 km resolution.

Figure 5 illustrates the comparison of lunar irradiance between the waxing and waning sides of the Moon. The lunar irradiance is derived from model data at the scale of 8 pixels/degree during a full moon when the absolute lunar phase angle is around 5 degrees. The average and variation of lunar irradiance under 32 wavelengths of ROLO filters for both the waning and waxing hemispheres are given in Figure 5a. It shows that the irradiance of the waxing side of the Moon is greater than that of the waning side due to larger areas of dark terrain types, which can be seen even with the naked eyes. The vertical bars represent the variation of lunar irradiance of the waning and waxing hemispheres. It can be seen that the variation is small, illustrating a small impact on the lunar irradiance due to the libration effect. Analysis of the libration effect will be shown in more detail in Section 3.2. Figure 5b shows the relative difference of the irradiance of moonlight between the waxing and waning sides of the Moon. The maximum relative difference is 14.85% ± 5.23% at 941.94 nm and the minimum is 10.19% ± 5.39% at 2383.15 nm.

2.4. Heterogeneous Correction Factor

Ideally, if the heterogeneity of the lunar surface did not exist, lunar irradiance at a specific distance would only be dependent on the lunar phase. A plot of lunar irradiance over waxing and waning lunar phases would produce a curve symmetrical about a y-axis value of the average irradiance, however, lunar surface heterogeneity disturbs this curve. In order to quantify the impact of heterogeneity on lunar irradiance, the heterogeneity correction factor is applied as follows:

$$tc\left(\alpha \right)=\frac{1}{1-\delta \left(\alpha \right)}$$

(11)

where $\delta \left(\alpha \right)$ represents the difference between the irradiance of homogeneous and heterogeneous lunar surfaces and is given as,

$$\delta \left(\alpha \right)=\frac{I_{hetero}\left(\alpha \right)-I_{homo}\left(\alpha \right)}{I_{hetero}\left(\alpha \right)}$$

(12)

where $I_{inhomo}\left(\alpha \right)$ and $I_{homo}\left(\alpha \right)$ indicate lunar irradiance of heterogeneous and homogeneous lunar surface, respectively, under a particular lunar phase angle α. According to Equations (11) and (12), the irradiance of an ideal homogeneous lunar surface can be corrected to that of the heterogeneous lunar surface using the heterogeneous correction factor as follows:

$$I_{hetero}\left(\alpha \right)=tc\left(\alpha \right)·I_{homo}\left(\alpha \right)$$

(13)

It can be seen from Equations (11)–(13) that if the value of the heterogeneous correction factor is close to one, the impact of heterogeneity is small. If it is far from one, the impact is large. Expanding the heterogeneous correction factor into the n-th-order polynomial form yields the following Equation (14):

$$tc\left(\alpha \right)=tc\left(0\right)+t{c}^{\prime }\left(0\right)\alpha +\frac{t{c}^{″}\left(0\right)}{2!}{\mathsf{\alpha }}^2+\cdots +\frac{t{c}^{\left(n\right)}\left(0\right)}{n!}{\alpha }^n$$

(14)

where the order of polynomial is determined based on the lunar phase coverage and the resolution of lunar observations.

The first-order polynomial of Equation (14) is called the first-order heterogeneous correction factor and the n-th-order polynomial is called the n-th-order heterogeneous correction factor.

3. Results

3.1. Comparison of Multiscale Lunar Images

The observation period should be long enough to cover the libration cycle. Therefore, the observation geometries from 1990 to 2010 are chosen to simulate lunar irradiance data in this study. Observation geometries whose absolute lunar phase angles are lower than 90 degrees (half-moon) are selected to perform the simulation. The comparisons between multiscale lunar irradiance data are shown in Figure 6. Since the scale (8 pixels/degree) reserves most details of texture and is the most accurate representation of the real lunar surface in the study, lunar irradiance at this scale is taken as a reference for lunar irradiance at other scales. The biases between the reference irradiance and irradiance at other scales are defined using the following formula:

$$\delta =\frac{I-I_{ref}}{I_{ref}}\times 100\%$$

(15)

where $I_{ref}$ represents lunar irradiance at the high scale (8 pixels/degree), and I indicate lunar irradiance at other scales.

It can be seen from Figure 6 that the bias increases as the resolution of model data decreases. The biases between the reference scale and other scales, including 4 pixels/degree, 2 pixels/degree, 1 pixel/degree, and 0.5 pixels/degree, are below 2% and the standard deviations of the differences are within 1%. The biases between these scales are almost the same throughout the 32 wavelengths of ROLO filters. However, the biases between the reference scale and the remaining scales range from 3 to 8.5% and show a greater difference than the previous scales throughout the 32 ROLO bands. The results demonstrate that heterogeneities at different scales exert different degrees of impact on the irradiance of moonlight, and that there is a threshold scale that separates the degree of impact. When the scales are above the threshold, the degree of impact shows little difference, however, when the scales are below the threshold, the degree of impact is large and shows obvious variation throughout the 32 ROLO bands. On the basis of the above comparison, the scale of 0.5 pixels/degree is chosen to serve as the threshold scale in this study.

3.2. The Evaluation of Libration Effect

Since the lunar surface visible to observers on Earth changes cyclically, the irradiance under different librations needs to be studied. On the basis of the model data, the influence of the libration effect can be easily determined. The best way to perform the evaluation is to use model data at the reference scale, however, this requires a sophisticated algorithm or high-performance machine, and excessive time. From Section 3.1, we can see that the biases of lunar irradiance between the reference scale and scales higher than 0.5 pixels/degree are within 2%. Therefore, the scale of 0.5 pixels/degree is sufficient to evaluate the libration effect. Lunar irradiance for different lunar phases and wavelengths are illustrated in Figure 7. The lunar phases are sampled at ±5, ±10, ±20, ±30, ±40, ±50, ±60, ±70, ±80, and ±90 degrees. Figure 7a,b show the time series of lunar irradiance at the 351.2 nm band for different waxing and waning lunar phases, respectively.

It can be seen that the libration effect causes the irradiance of the Moon to fluctuate slightly from its mean. The magnitude of the fluctuation under all 32 ROLO bands is very small, ranging between 0.79% and 1.46% during waxing lunar phases, and 0.82% and 2.39% during waning lunar phases, which is quantified by the standard deviation relative to the average lunar irradiance. The uncertainties (1δ/mean) of lunar irradiance for the ±5 and ±90 lunar phases and 32 wavelengths of ROLO filters are shown in

Table 3. Uncertainties of lunar irradiance at ±5 lunar phase angle.

Band	1	2	3	4	5	6	7	8
Uncertainty (%)	1.05 0.98	1.08 1.01	1.06 0.99	1.09 1.02	1.07 1.01	1.05 0.99	1.10 1.03	1.07 1.00
Band	9	10	11	12	13	14	15	16
Uncertainy (%)	1.06 0.99	1.09 1.02	1.05 0.99	1.06 0.99	1.01 0.94	1.03 0.96	1.05 0.99	1.00 0.93
Band	17	18	19	20	21	22	23	24
Uncertainty	1.03 0.96	1.04 0.97	1.06 1.00	1.07 1.00	1.07 1.00	1.11 1.04	1.11 1.04	1.15 1.07
Band	25	26	27	28	29	30	31	32
Uncertainty (%)	1.04 0.97	0.98 0.91	0.91 0.85	0.91 0.85	0.97 0.90	0.90 0.83	0.88 0.81	0.86 0.79

and

Table 4. Uncertainties of lunar irradiance at ±90 lunar phase angle.

Band	1	2	3	4	5	6	7	8
Uncertainty (%)	2.25 1.04	2.28 1.05	2.32 1.07	2.22 1.04	2.31 1.06	2.20 1.03	2.33 1.07	2.31 1.06
Band	9	10	11	12	13	14	15	16
Uncertainy (%)	2.22 1.04	2.31 1.06	2.31 1.06	2.32 1.06	2.14 1.01	2.25 1.04	2.25 1.04	2.13 1.01
Band	17	18	19	20	21	22	23	24
Uncertainty (%)	2.22 1.04	2.25 1.04	2.22 1.04	2.34 1.07	2.36 1.08	2.38 1.08	2.39 1.08	2.23 1.04
Band	25	26	27	28	29	30	31	32
Uncertainty (%)	2.19 1.03	2.06 0.99	1.91 0.94	1.93 0.95	1.96 0.96	2.22 1.04	1.84 0.92	1.77 0.90

. The number on the first row in each cell indicates the uncertainty during the waning lunar phase, whereas the number on the second row represents the uncertainty during the waxing lunar phase. We can see that the uncertainty of lunar irradiance during the waning lunar phase is always higher than that during the waxing lunar phase due to greater variation of the heterogeneous lunar surface on the waning hemisphere, which will be discussed in Section 3.3. The results shown in Table 3 and Table 4 indicate that the uncertainty of lunar irradiance changes slightly with the variation of wavelength. Therefore, it can be inferred that the libration effect is wavelength independent. The evaluation results for this study are in agreement with the results in [33].

3.3. Heterogeneous Correction Factors at Different Scales

The heterogeneous correction factors under different lunar phases are calculated by comparing heterogeneous and homogeneous lunar surfaces. The irradiance of the homogeneous lunar surface is derived by mixing maria and highland solar phase functions in a combination that is consistent with the measured spectrum and albedo of the Apollo 16 landing site. The fraction of highland is 84% and the fraction of maria is 16% [22]. Figure 8a shows four examples of model data with heterogeneity taken into consideration. The lunar phases of these examples are 45, 90, −45, and, −90 degrees from left to right, respectively. The corresponding model data without consideration of topographic information is shown in Figure 8b. Figure 8c shows corresponding examples without the influence of heterogeneity. The model data in Figure 8 are generated at high resolution (8 pixels/degree).

The heterogeneous correction factor derived using Equations (11) and (12), and the results of six bands (351.2 nm, 474.9 nm, 745.3 nm, 941.9 nm, 1243.2 nm, and 2125.5 nm) at the scale of 8 pixels/degree, are shown as examples in Figure 9. The vertical bars for each lunar phase represent the standard deviation of the heterogeneous correction factors, and the curved line represents the mean heterogeneous correction factor. The mean heterogeneous correction factor under the four ROLO bands ranges from 0.8155 to 0.9321, 0.8113 to 0.9309, 0.8242 to 0.9347, 0.8168 to 0.9325, 0.8292 to 0.9361, and 0.8192 to 0.9338, respectively. We can see that the heterogeneous correction factors between each adjacent lunar phase show good consistency since almost all the texture information has been retained at a high scale. The results show that the heterogeneous correction factors for different lunar phases at the four ROLO bands exhibit different forms of curved line. It can be seen that the factor is lower than one under all lunar phases since the irradiance of the homogeneous lunar surface is greater than that of the heterogeneous lunar surface. The further the value deviates from one, the greater the impact of heterogeneity on the lunar irradiance. It also shows that the factor during the waxing lunar phase is greater than that during the waning lunar phase; the other 28 bands also show the same trend, indicating less impact of heterogeneity of the lunar surface on the irradiance of moonlight during waxing lunar phases than during waning lunar phases.

The heterogeneous correction factors at eight different scales at 351.19 nm are shown in Figure 10a–h. The factors with and without the influence of topography are plotted in each figure. Figure 10i illustrates the absolute relative difference between factors with and without consideration of topography. The result is derived at a high scale of 8 pixels/degree, as shown in Figure 10a. Figure 10a–c and i demonstrate that the topography of the lunar surface exerts a greater impact on lunar irradiance during waxing lunar phases, which is in agreement with the results shown in Table 2, indicating larger variation of topography in the waning hemisphere. The results indicate that the degree of impact due to topography decreases as the resolution of lunar images decreases, which can be seen from images Figure 10a–g, in which the curved lines with and without the influence of topography gradually coincide. Therefore, the lower the resolution of the lunar image, the less impact of lunar topography on lunar irradiance. From Figure 10a–h, we can see that the heterogeneous correction factors increase from 0.82 ± 0.02 to 0.93 ± 0.01 at a scale of 8 pixels/degree and from 0.89 ± 0.01 to 1.00 ± 0.01 at a scale of 0.083 pixels/degree. The trends indicate that the heterogeneous correction factor increases as the resolution decreases. The greater the heterogeneity of the Moon, the further the factor away from one, indicating the higher degree of the impact on lunar irradiance. The heterogeneous correction factors plotted in Figure 10a–g are shown to be scale independent, indicating the ability to measure the influence of heterogeneities on the irradiance of moonlight at different scales. The heterogeneous correction factors plotted in Figure 10h, however, show greater linearity than the other images since too much texture detail is lost and the high-order terms in Equation (14) are insignificant. Figure 10i shows that the influence of topography is very small even at the highest resolution since the observer is too far away from the Moon. The average influence is greater during the waxing lunar phases than the waning lunar phases and reaches its maximum around the half-moon lunar phases.

4. Discussion

4.1. The Challenge of the Study

Two challenges are involved in this study as follows: the creation of a texture function of the lunar surface under different illumination and viewing angles, and the quantitative evaluation of the impact of heterogeneity on lunar irradiance. The lunar surface is heterogeneous from physical and chemical perspectives, and therefore the influence of heterogeneity needs to be studied and taken into account in lunar irradiance models. One method of conducting the experiment is to make accurate observations of the Moon, remove the influence of heterogeneity, and compare the difference of lunar irradiance with and without the influence of heterogeneity. However, the correction algorithm does not fully remove the impact due to heterogeneity. Another method is to create model data with and without the influence of heterogeneity and compare the difference between them, however, this method is also challenging, particularly in building the texture function under different illumination and viewing angles. Fortunately, previous studies by many researchers have paved the way to the solution. In [20], the lunar surface was divided into three groups, and a photometric model was created for each group based on SELENE/SP data. The texture functions of the lunar surface under different illumination and viewing angles at 1° × 1° resolution meshes were created. Similarly, Wu et al. (2013) [21] divided the lunar surface into four categories based on the mineral contents of FeO; the photometric model of each category was created and used to remove the geometric effect. The result indicated that corrected reflectance at two adjacent orbits showed better consistency than the uncorrected reflectance.

The Robotic Lunar Observatory program [34] at the US Geological Survey in Flagstaff, Arizona, acquired thousands of lunar data points. On the basis of these observations, the ROLO lunar irradiance model was established and has been applied to the radiometric calibration of on-orbit sensors, including SeaWiFS, MODIS, VIIRS, and MSS [9]. The photometric models of two important terrain types of lunar surface have been created using the ROLO dataset [22]. By dividing the lunar surface into two categories and calculating the reflectance of each category using a photometric model, the texture function of the lunar surface under different illumination and viewing angles was created in this study.

Another difficulty involves the quantitative evaluation of the impact of heterogeneity on lunar irradiance. In this study, a texture function of the lunar surface is established so that the heterogeneous lunar surface can be modeled. The heterogeneous correction factor is defined by comparing lunar irradiance with and without the influence of heterogeneity. The imaging sensors are manufactured with different resolutions, therefore, the impact of multiscale heterogeneities on lunar irradiance are of particular interest. Multiscale lunar irradiance data are created and the heterogeneous correction factors at different scales are compared and analyzed in this study.

4.2. The Analysis of the Results

In order to study the impact of heterogeneity of the lunar surface on the irradiance of moonlight and provide the basis for improving lunar irradiance models, lunar model data with and without the influence of heterogeneity are created in this study. Multiscale DEMs data are created at first, and the photometric models based on the ROLO dataset of two typical terrain types on the lunar surface are used to determine the intensity of each point on lunar surface. An algorithm is developed to determine the near side of the Moon. Then, the irradiance of moonlight is computed by integrating over the lunar surface that faces the imager. The heterogeneous correction factor is defined and computed for each lunar phase based on the model data. Finally, evaluation of the libration effect is performed and the measurement of the influence of heterogeneity on lunar irradiance is made.

The average and standard deviation of the slope for each multiscale DEM data point decrease as the scale is reduced, however, this trend does not demonstrate a unique pattern that can be used to determine the threshold scale. Since the combined topography and composition of the lunar surface determine the optical properties of the Moon, it is hard to determine the threshold scale solely based on topographic parameters. When model data at eight different scales are created, a scale of 8 pixels/degree is selected as a reference scale for the comparison between multiscale lunar irradiance data since it is the most accurate representation of the lunar surface, in this study. Compared with the lunar irradiance at the reference scale, the irradiance at scales of 4 pixels/degree, 2 pixels/degree, 1 pixel/degree, and 0.5 pixels/degree is below 2%, while the lunar irradiance at the remaining scales is between 3% and 8%. Therefore, the scale of 0.5 pixels/degree is chosen as the threshold scale.

The libration effect is evaluated using the threshold scale to save computation cost and time. Observation geometries from 1990 to 2010 whose absolute lunar phases were lower than 90 degrees are selected to perform the evaluation. Since the lunar surface is heterogeneous due to topography and different mineral and chemical compositions at different locations, the near side of the lunar surface needs to be determined at each lunar phase, which is accomplished using a newly developed algorithm in this study. The results show that the libration effect exerts a small impact on the irradiance of moonlight, with only 0.94 to 2.33% uncertainty throughout the 32 ROLO bands. It can be concluded from the results that the libration effect is wavelength independent.

By defining a heterogeneous correction factor, the influence of the heterogeneous lunar surface on lunar irradiance can be quantified. The heterogeneous correction factor at a high scale of 8 pixels/degree is the lowest among all scales, ranging between 0.8 and 0.95 over all the selected lunar phases, indicating it is the most vulnerable scale to heterogeneity. This is reasonable since the high scale reserves most details of texture and is the most accurate representation of the lunar surface in this study. As the resolution decreases, the heterogeneous correction factor increases and gradually approaches one. The results demonstrate that the heterogeneity of the lunar surface exerts less influence on lunar irradiance at lower resolution. Another finding is that the curved line, namely, the plot of the heterogeneous correction factor for different lunar phases, shows many similarities between the previous seven scales, with excellent consistency and curvature between each adjacent lunar phase, however, the curved line at the low scale of 0.083 pixels/degree shows less consistency between each adjacent lunar phase and demonstrates greater linearity than the previous seven scales. The reason behind this result is that the lowest scale reserves the least information as compared with the other scales, and therefore the high-order terms in Equation (14) are insignificant. From the curved line derived for all eight scales, the heterogeneous correction factor is always greater during the waxing lunar phases than during the waning lunar phases, representing a smaller degree of influence due to heterogeneity on the waxing hemisphere than that on the waning hemisphere. The curved line with and without the influence of lunar topography is compared and the results show that as the resolution decreases, the influence of lunar topography on lunar irradiance also decreases due to the loss of topographic information. The comparison at the highest resolution shows that lunar topography exerts little impact on lunar irradiance since the observer is too far away from the Moon.

The original MT2009 lunar irradiance model does not differentiate the waxing and waning lunar phases, and the irradiance of moonlight produced by the model is symmetrical during the waxing and waning lunar phases, which is in agreement with the model data without the influence of heterogeneity. Therefore, the results shown in Section 3.3 provide a basis to correct the MT2009 lunar irradiance model. Miller et al. (2014) [24] compared the MT2009 lunar irradiance model to the lunar irradiance data from Meteosat Second Generation (MSG) for 0.6 and 0.8 μm bands. They used a sixth-order polynomial function to fit the percent error and corrected the MT2009 lunar irradiance model. The corrected MT2009 lunar irradiance model greatly reduces the lunar phase dependence on the night-time reflectance of Salar de Uyuni. Zeng et al. (2017) [25] compared the MT2009 lunar irradiance model to the lunar irradiance data from the Sea-Viewing Wide Field-of-View Sensor (SeaWiFS) at its eight bands. Since SeaWiFS lunar observations are limited by their resolution and lunar phase coverage, they used a one-order polynomial function to fit the percent error and corrected the MT2009 lunar irradiance model. The corrected MT2009 lunar irradiance model also removes the lunar phase dependence from the night-time reflectance of the Dome-C site.

4.3. Limitations

There are a number of limitations in this study. First, the lunar surface is only divided into two categories, namely, maria and highland, due to the absence of global reflectance of the lunar surface. The plot line of the heterogeneous correction factor may show a different curvature under some lunar phases if the lunar surface is divided into much finer categories. Secondly, the Lommel–Seeliger model does not take into account scattering of diffuse light that has made its way indirectly to the same position by being scattered one or more times. Therefore, multiple scattering due to the topography of lunar surface is less considered in the simulation of lunar irradiance data. Thus, different photometric models could be tried in the future. Finally, the opposition effect is not discussed in this study. The photometric model takes the opposition effect into consideration by including an exponential term in the polynomial equation. Therefore, lunar model data is created even for small lunar phases, however, lunar irradiance does not exhibit an obvious surge at small lunar phase angles. Since the mechanism of the opposition effect is quite complicated, extensive studies have been performed to explain it [35,36,37].

5. Conclusions

Since the radiometric property of the Moon is very stable, it has been used as a standard light source by many on-orbit sensors, including SeaWiFS, MODIS, and VIIRS. In order to perform lunar calibration, the construction of an accurate lunar irradiance model is necessary. The irradiance of moonlight is mainly determined by the lunar phase angle, however, due to the existence of heterogeneity on the lunar surface, the change of lunar irradiance with the variation of the lunar phase is complicated. In order to evaluate the influence of the heterogeneous lunar surface on the irradiance of moonlight, model data at eight different scales are created using the Lommel–Seeliger photometric model based on the lunar observations of ROLO. The threshold scale is determined by comparing lunar irradiance at eight different scales at first. Then, the libration effect is evaluated based on model data at the threshold scale of 0.5 pixels/degree, and the result shows that only 0.94% to 2.33% of uncertainties embedded in lunar irradiance are caused by the libration effect. Finally, a heterogeneous correction factor is defined to measure the degree of influence of heterogeneity on lunar irradiance. On the basis of the multiscale model data under observation geometries from 1990 to 2010, the heterogeneous correction factor is calculated. Four conclusions can be made based on the analysis of the heterogeneous correction factor. First, the heterogeneity embedded in the waning hemisphere exerts a greater impact on the irradiance of moonlight than that in the waxing hemisphere under 32 wavelengths of ROLO filters. Second, the heterogeneous correction factors increase and approach one as the resolutions are reduced, indicating less influence of heterogeneity at lower resolutions on lunar irradiance. Third, the heterogeneous correction factor is scale independent. Finally, lunar topography exerts little impact on lunar irradiance since the observer is too far away from the Moon.

The results of this study support the improvement of the MT2009 lunar irradiance model, undertaken to improve its consideration of topography and the heterogeneous surface [10]. The corrected lunar irradiance model has been applied to the field of night-time remote sensing. Compared with the original model, the corrected MT2009 lunar irradiance model greatly reduces uncertainty introduced by the heterogeneous lunar surface [22,23].