1. Introduction
Owing to various issues and challenges related to land cover classification (LCC) [
1,
2] and the wide application of land cover data as basic inputs in various interdisciplinary studies [
3,
4,
5], LCC has been a very popular topic in remote sensing [
3,
4,
6]. Fine LCC (FLCC) of complex landscapes drew increasing attention [
7,
8,
9,
10,
11] owing to landscape-specific characteristics and their accompanying issues. LCC of complex open pit mining and agricultural development landscapes (CMALs) was studied previously [
12,
13,
14]. In particular, Li et al. [
12] conducted fine classification of three open pit mining lands, and Chen et al. [
13] reviewed FLCC of open pit mining landscapes by using remote sensing data. However, the FLCC of CMALs has not been investigated. This is significant for the scientific management of mines and agricultural development.
Three significant landscape-specific characteristics seriously limit the accuracy of FLCC of CMALs [
12,
13,
14]: significant three-dimensional terrain [
15,
16]; strong spatio–temporal variability [
17,
18]; and spectral–spatial homogeneity. Methods to reduce these characteristics were identified. These include the extraction of effective features [
12,
13,
19,
20,
21] and feature sets [
13,
14,
22] with feature reduction (FR) [
12] and feature selection (FS) [
12,
13,
14,
23] and the construction of powerful classification models [
13].
Many low-level handcrafted features were proven to be effective for the LCC of CMALs [
12,
13,
14] (e.g., texture and filter features and topographic information). Moreover, fusion of these features is necessary and one of the most effective approaches for this purpose. Currently, data fusion [
24,
25] is one of the most studied areas in remote sensing owing to the easy acquisition of multi-source data and its success in classification tasks. In particular, multimodal data fusion [
26,
27], such as the fusion of optical image and topographic data, is helpful for the LCC of complex landscapes. The development of multimodal data fusion can be partly attributed to the rapid development of light detection and ranging (LiDAR) [
7,
19,
28,
29,
30,
31] and stereo satellite sensor [
12] technologies. However, simple fusion methods, such as stacking all the features, are far from yielding sufficient information for the FLCC of CMALs.
Deep learning (DL) algorithms, which can be used to extract deep and discriminative features layer by layer, have become increasingly popular in machine learning and remote sensing [
32,
33,
34]. The most typical DL algorithms are the deep belief network (DBN), the autoencoder [
35,
36,
37,
38], and the convolutional neural network (CNN) [
39,
40,
41,
42,
43,
44]. In particular, DBN [
45,
46] is one of the most widely used DL algorithms in various communities. This is due to DBN’s unsupervised learning ability in feature extraction, which has a very low demand for labeled data in high-accuracy classification tasks. Consequently, DBNs were examined for remote sensing applications in some studies. For example, Chen et al. [
47] first proposed the paradigms of spectral, spatial, and spectral–spatial feature-based DBNs for the classification of hyperspectral images. Zhao et al. [
48] introduced a novel unsupervised feature learning method to classify synthetic aperture radar images based on a DBN algorithm and ensemble learning. In addition, Zou et al. [
49] used a DBN algorithm to select features for remote sensing scene classification. Basu et al. [
50] proposed a DBN-based framework for the classification of high-resolution scene datasets. Subsequently, Chen et al. [
51] used a DBN algorithm to classify high-resolution remote sensing images. However, DBNs have not been investigated for FLCC, especially for CMALs.
Machine learning algorithms (MLAs) have been widely used for remote sensing image classification in complex landscapes. For example, Attarchi and Gloaguen [
52] had compared random forest (RF), support vector machine (SVM), neural network (NN), and maximum likelihood algorithms for classifying complex mountainous forests. Abdi [
53] used RF, SVM, extreme gradient boosting, and deep NN for land cover and land use classification in complex boreal landscapes. Dronova et al. [
54] applied NN, decision tree (DT), k-nearest neighbour (KNN), and SVM to delineate wetland plant functional types. Zhao et al. [
55] combined a CNN model and a DT method for mapping rice paddies in complex landscapes. Some MLAs were employed to classify complex open pit mining landscapes [
30,
31,
56] and CMALs [
12]. Li et al. [
12] compared RF, SVM, and NN. Maxwell et al. [
30] assessed RF, SVM, and boosted classification and regression tree (CART). Maxwell et al. [
31] used RF, SVM, boosted CART, and KNN. The results showed that the RF and SVM algorithms were more effective and robust than the other investigated algorithms. Naturally, combining DBNs with powerful MLAs may be worthwhile. In the remote sensing domain, some typical studies were conducted and yielded good results. For example, Zhong et al. [
57] proposed a model for hyperspectral image classification by integrating DBN and conditional random field (CRF) algorithms (in the form of a DBN-CRF algorithm). Chen et al. [
47] and Le et al. [
58] combined the DBN algorithm and logistic regression (LR) to obtain a DBN-LR algorithm. Furthermore, Ayhan and Kwan [
59] compared the DBN algorithm with a spectral angle mapper (SAM) and SVM. Qin et al. [
60] developed a combined model based on a restricted Boltzmann machine (RBM, a basic component of a DBN) and an adaptive boosting (AdaBoost) algorithm, called the RBM-AdaBoost model. He et al. [
61] combined a deep stacking network (DSN) similar to a DBN and LR (DSN-LR). Thus, ensembles of DBNs and MLAs, which includes the above-mentioned approaches that are helpful for FLCC of CMALs, are worth exploring.
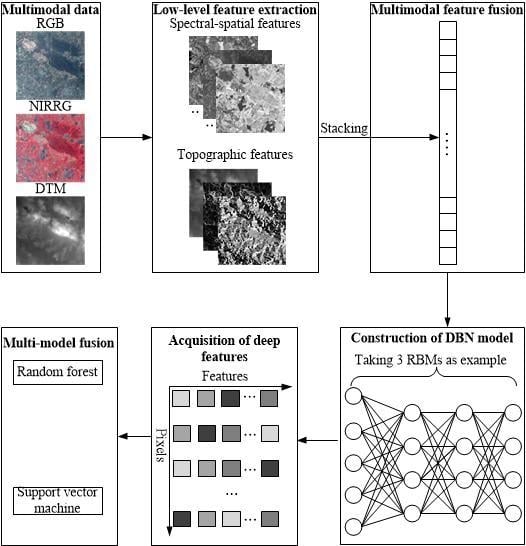
In this study, a novel multimodal and multi-model deep fusion strategy was proposed for the FLCC of CMALs and was tested on a CMAL in Wuhan City, China by using ZiYuan-3 (ZY-3) stereo satellite imagery. Multiple low-level multimodal features including spectral–spatial and topographic information were first extracted and fused. The features were then entered into a DBN model for deep feature learning. Finally, the developed deep features were fed to RF and SVM algorithms (hereafter referred to as the DBN-RF and DBN-SVM algorithms, respectively) for classification. Three groups of comparison experiments were conducted: deep features with the softmax classifier (hereafter referred to as DBN-S); low-level features with the RF and SVM algorithms; and low-level features with FS, RF, and SVM algorithms (hereafter referred to as the FS-RF and FS-SVM models, respectively). Five groups of training, validation, and test sets with some spatial auto-correlations [
62] were randomly constructed for parameter optimization, model development, and accuracy assessment. In particular, a spatially independent test set was examined. Moreover, statistical tests were conducted to investigate whether the proposed strategy yielded significant improvements.
4. Results
Figure 6 presents the FS, parameter optimization, and accuracy assessment processes. Based on five groups of training, validation, and test sets (
Figure 6a), FS yielded two feature subsets, both with 34 features (
Figure 6b, for details see
Section 4.1). In the parameter optimization process, only the first group of training and validation sets was used for the DBN-based models (
Figure 6(c1)). First, the
depth and
node were optimized for the DBN-S model using five different random initializations of the DBN (
Section 4.2.1). Based on the optimized DBN, the
mtry,
cost, and
gamma parameters were optimized for the DBN-RF and DBN-SVM models (
Section 4.2.2). Owing to the randomness of the RF algorithm, five trials were performed to obtain the optimal parameters of the DBN-RF model. Five groups of training and validation sets were used to optimize the MLA-based models (
Figure 6(c2), for details see
Section 4.2.3). For the RF and FS-RF models, an optimized value of
mtry was obtained for each group of data sets based on five random runs. For the SVM and FS-SVM models, the same values of
cost and
gamma were obtained for all five groups of data sets based on five runs. Because the first and third groups of data sets yielded the same feature subset, the second, fourth, and fifth groups of data sets yielded another one. The parameter optimization of FS-RF is displayed separately for each case in
Figure 6(c2). In the model assessment process, five test sets were used (
Figure 6d, for details see
Section 4.3). In total, there was just one DBN-S, DBN-RF, and DBN-SVM model. However, there were five RF, SVM, FS-RF, and FS-SVM models for five groups of training, validation, and test sets, respectively. Owing to the randomness of the DBN and RF algorithms, each test set yielded five sets of accuracies for the DBN-S, DBN-RF, DBN-SVM, RF, and FS-RF models. Then, the final accuracies of those models were averaged 25 times, and five times for the SVM and FS-SVM models. For the independent test set, some models were used to obtain only a group of accuracies for comparison (
Section 4.5).
4.1. Feature Subsets for MLA-Based Classification
Based on the FS procedure, the five random training sets yielded two different feature subsets that had a different feature importance. Training sets 1 and 3 yielded feature subset 1; the average and standard deviation values of the mean decrease in accuracy for each feature were calculated (
Figure 7). Training sets 2, 4, and 5 yielded feature subset 2; the average and standard deviation values of the mean decrease in accuracy for each feature were also calculated (
Figure 7). Similar to Li et al. [
12], about 32% of the features (i.e., 34) were selected for almost all types.
4.2. Parameter Optimization Results
4.2.1. Parameter Optimization for DBN-S
For deep feature extraction using the DBN-S model, two parameters were optimized. The first group of training and validation sets was used, and the process was repeated five times. The
depth was set between 1 and 6, and the
node was set to one group of values (50, 150, 350, 500, 800, 1500, and 2000). Moreover, to simplify the optimization process, it was assumed that the
node was the same in each hidden layer. Meanwhile, the activation function,
,
epoch, and the mini-batch size were set to sigmoid, 0.0001, 800, and 2048, respectively. The combination of 5 and 1500 was selected for the
depth and
node (
Table 4), which yielded the highest average OA of 94.19% ± 0.39% for validation set 1. The average and standard deviation of the OA for validation set 1 derived from different parameter combinations are depicted in
Figure 8.
4.2.2. Parameter Optimization for Multi-Model Fusion
For the multi-model fusion of the DBN algorithm and MLAs, the parameters for the MLAs were optimized. With respect to the DBN-RF model, since the optimized value of the
node was 1500, the value of
mtry ranged from 100 to 1500 in steps of 100. Finally, the optimal value of
mtry was determined to be 100 (
Table 4), which yielded the highest average OA of 94.22% ± 0.02%.
For the fused DBN-SVM model,
cost and
gamma were optimized. In total, 48 combinations were used, i.e., eight values (
) of
cost and 10 (
) of
gamma [
12]. The optimal parameter combination was determined to be
cost =
and
gamma =
(
Table 4), which yielded the highest OA of 94.97%.
4.2.3. Parameter Optimization for MLAs
For the MLA-based models, three parameters were optimized. For the RF and FS-RF models,
mtry ranged from 1 to 34 and 1 to 106, respectively, in steps of 1. For the SVM and FS-SVM models, the parameter spaces were the same as those described in
Section 4.2.2.
With respect to the RF-based models, five repeated runs were performed for each data set to achieve specific parameters. However, for the SVM-based models, five runs were performed for all of the data and the averaged results were used to determine the optimal parameter combinations. As a result, for data sets 1, 2, 3, 4, and 5 with all of the features, the
mtry values were 60, 53, 68, 56, and 55, which correspond to average OAs of 88.85% ± 0.09%, 89.49% ± 0.11%, 89.21% ± 0.07%, 89.02% ± 0.09%, and 88.86% ± 0.10%, respectively (
Table 5). For those with feature subsets, the optimized values of
mtry were 19, 18, 22, 17, and 15, which correspond to average OAs of 89.98% ± 0.06%, 91.05% ± 0.02%, 90.31% ± 0.07%, 90.72% ± 0.05%, and 90.39% ± 0.05%, respectively (
Table 5). For all of the data with all of the features, the combination of
and
for
cost and
gamma with an accuracy of 78.05% ± 0.47% was achieved (
Table 5). For those with feature subsets, the combination of
and
for
cost and
gamma with an accuracy of 92.35% ± 0.35% was acquired (
Table 5).
4.3. Accuracy Assessment and Analysis of Five Random Test Sets
4.3.1. Overall Performance
The time of each model based on the first group of training, validation, and test sets presents in
Table 6. The long-time of FS-RF and FS-SVM was attributed to the feature selection process, which took 1.93 h. The parameter optimization process needed more time than the model training and prediction. The convergence process diagram of DBN-S depicts in
Figure 9. When the iteration number reached 500 the model was stable.
The overall performance of the different models based on the OA, Kappa, and F1-score are shown in
Table 7. The percentage deviations of the three metrics between the models are presented in
Table 8.
For the MLA-based models, the OA decreased in the order of 91.77% ± 0.57% (FS-SVM), 90.39% ± 0.42% (FS-RF), 88.90% ± 0.20% (RF), and 77.88% ± 0.53% (SVM). The order is the same for Kappa and the F1-score. The best model was determined to be the FS-SVM model. It is clear that FS improved the classification accuracy. After FS, the OA, Kappa, and F1-score improvements of 1.68%, 1.79%, and 1.69%, respectively, were achieved for the RF-based model (
Table 8). Compared to the SVM model, the FS-SVM model considerably improved the OA, Kappa, and the F1-score, by 17.84%, 19.06%, and 17.95%, respectively (
Table 8). For the models based on all of the features, the RF model was better than the SVM model, yielding improvements of 14.15%, 15.11%, and 14.22% in the OA, Kappa, and the F1-score, respectively (
Table 8). However, for the models based on feature subsets, the FS-SVM model slightly outperformed the FS-RF model (
Table 8).
For the deep feature-based models, the OA decreased in the order of 94.74% ± 0.35% (DBN-SVM), 94.23% ± 0.67% (DBN-S), and 94.07% ± 0.34% (DBN-RF). The order is the same for Kappa and the F1-score. The best model was determined to be the DBN-SVM. Moreover, after model fusion, improvements of 0.54%, 0.56%, and 0.53% were achieved in the OA, Kappa, and the F1-score, respectively (
Table 8). However, compared with the DBN-S model, the DBN-RF model slightly decreased the classification accuracies (
Table 8).
Compared to the best MLA-based model, the FS-SVM model, all of the deep feature-based models yielded higher classification accuracies. The DBN-S model yielded improvements of 2.60%, 2.76%, and 2.60% in the OA, Kappa, and the F1-score, respectively (
Table 8). The improvements for the OA, Kappa, and the F1-score were 2.46%, 2.59%, and 2.46% when the DBN-RF model was used and 3.15%, 3.33%, and 3.15% when the DBN-SVM model was employed, respectively. (
Table 8).
4.3.2. Class-Specific Performance
The class-specific performance of the different models based on the F1-measure are displayed in
Table 9. The percentage deviations between the models are shown in
Table 10.
For the F1-measures for almost all of the classes, the performance of the MLA-based models (
Table 9) decreased in an order that agrees with the conclusion drawn in
Section 4.3.1. There are only three exceptions: for woodland, shrubbery, and ore processing site, the FS-RF model outperformed the FS-SVM model (i.e., the percentage deviations are negative in column D of
Table 10). Similarly, for the F1-measures of almost all of the classes, the performance of the deep feature-based models (
Table 9) decreased in an order that agrees with the conclusion drawn in
Section 4.3.1 with only five exceptions. For fallow land, woodland, shrubbery, pond and stream, and mine pit pond, the DBN-RF model outperformed the DBN-S model (i.e., the percentage deviations are positive in column H of
Table 10). For the F1-measures of all of the classes, all of the deep feature-based models outperformed the best MLA-based model, i.e., the FS-SVM model (
Table 9).
For the highest F1-measure of each land cover type derived from the MLA-based models, most achieved an accuracy over 90% (
Table 9), i.e., paddy, greenhouse, coerced forest, nursery, pond and stream, mine pit pond, dark road, bright road, red roof, blue roof, bare surface, open pit, and dumping ground. Only six and one classes achieved over 80% and 70% accuracy, respectively (
Table 9), i.e., green dry land, fallow land, woodland, shrubbery, light gray road, and ore processing site and bright roof. For the highest F1-measure of each land cover type derived from the deep feature-based models, almost all of the classes achieved over 90% accuracy and only three over 80% (
Table 9), i.e., fallow land, shrubbery, and bright roof.
The percentage deviations between the RF and SVM models for the different types of land cover are presented in column A of
Table 10. As demonstrated in
Table 10, the RF algorithm significantly outperformed the SVM algorithm. The percentage deviations range from 1.40% to 29.61% with an average of 15.39%. Moreover, 60% of the land cover types exhibited over 10% deviation, i.e., green dry land, fallow land, woodland, shrubbery, nursery, pond and stream, light gray road, bright roof, bare surface, open pit, ore processing site, and dumping ground.
FS resulted in positive effects for the accuracies of all of the classes (columns B and C of
Table 10). For the RF-based models, the percentage deviations range from 0.28% to 3.27% with an average of 1.73%. However, for the SVM-based models, the percentage deviations are very large, ranging from 4.63% to 36.90% with an average of 19.19%. Moreover, 75% of the land cover types exhibited over 10% deviation, i.e., paddy, green dry land, fallow land, woodland, shrubbery, coerced forest, nursery, pond and stream, mine pit pond, light gray road, bright roof, bare surface, open pit, ore processing site, and dumping ground.
In general, the FS-SVM model outperformed the FS-RF model for almost all of the land cover types (column D of
Table 10). Only three exceptions exist, i.e., woodland (−0.69%), shrubbery (−0.47%), and the mineral processing site (−0.70%). For the other classes, the percentage deviations range from 0.11% to 4.43% with an average of 1.94%.
For all of the classes, the percentage deviations between all the deep feature-based models and the FS-SVM model are positive (columns E–G of
Table 10). For the DBN-S, DBN-RF, and DBN-SVM models, the percentage deviations range from 0.11% to 9.69% with an average of 2.79%, from 0.17% to 8.61% with an average of 2.61%, and from 0.19% to 10.38% with an average of 3.36%, respectively.
Among the deep feature-based models, the DBN-S model outperformed the DBN-RF model for almost all of the classes (column H of
Table 10). Also, the DBN-SVM model outperformed the DBN-S model for all of the classes (column I of
Table 10). For the percentage deviations between the DBN-RF and DBN-S models, only five exceptions exist, i.e., fallow land (0.11%), woodland (0.23%), shrubbery (0.05%), pond and stream (0.04%), and mine pit pond (0.06%). For the other classes, the percentage deviations range from −0.98% to −0.10% with an average of −0.27%. Meanwhile, the percentage deviations between the DBN-SVM and DBN-S models range from 0.07% to 1.12% with an average of 0.55%.
4.3.3. Statistical Tests
Statistical tests were performed on the pairs of results predicted for test set 1 using seven models. For the RF and DBN-based models, results with OAs closer to the average values of five random runs were selected. For the SVM and FS-SVM models, the individual results were directly used (
Table 11).
Table 12 shows the chi-square and
p values between the different models. If the chi-square value is greater than 30.14, a statistical significance exists at the 95% confidence level (
p < 0.05). The statistical tests revealed the following. (1) The RF algorithm was significantly better than the SVM algorithm (with chi-square and
p values of 89.14 and 0.00, respectively). (2) FS had different effects on different algorithms. There was no significant difference between the FS-RF and RF algorithms (with a
p value of 0.15); however, a significant difference was observed between the FS-SVM and SVM algorithms, with chi-square and
p values of 46.21 and 0.00, respectively. (3) Although the average OA difference between the FS-SVM and FS-RF algorithms was not large, a significant difference was observed (with chi-square and
p values of 55.94 and 0.00, respectively). (4) All the deep feature-based models significantly outperformed the best MLA-based model, i.e., the FS-SVM model. (5) Among the three deep models, the fused DBN-SVM model significantly outperformed the DBN-S model (with chi-square and
p values of 31.70 and 0.03, respectively), and there was no significant difference between the DBN-S and DBN-RF models, (with chi-square and
p values of 25.57 and 0.14, respectively).
4.4. Visual Assessment of Predicted Maps
For the CMAL, the FLCC map predicted based on the DBN-SVM model and the LCC maps based on the DBN-SVM and FS-RF models [
12] are illustrated in
Figure 10. The LCC map that predicted by using the DBN-SVM model was derived by grouping the FLCC results into seven first-level classes. The LCC map that predicted based on the FS-RF model was obtained from [
12]. Some classes in the LCC results derived from the FS-RF model are superior to those from the DBN-SVM model. The main differences are the misclassification of roads, residential land, and bare surfaces as open pit mining land. Besides the spectral similarity among those land cover types, two main factors caused those differences. (1) The training samples for open pit mining land in [
12] were randomly selected from all the open pit mining land in the study area; however, the samples used in this study were obtained from a very small subset of all of the open pit mining land (
Table 2). Consequently, the spatial auto-correlation [
62] significantly contributed to the results obtained using the FS-RF model [
12]. (2) Compared to the FS-RF model, the DBN-SVM model normalized the stacked multimodal features. This might have weakened the advantages of the topographic information and resulted in misclassification of the above-mentioned land cover types. The other classes such as water, crop land, and forest land were classified better in the LCC map derived from DBN-SVM.
For the FLCC, besides the misclassification of the above-mentioned first-level classes, there was misclassification within some second-level classes. For example, many pond and stream pixels were incorrectly classified as mine pit pond pixels. In addition, many dumping ground and ore processing site pixels were misclassified as open pit pixels. These misclassifications were also attributed to the two above-mentioned factors.
4.5. Accuracy Assessment and Statistical Tests for Independent Test Set
For the independent test set, the best MLA-based model in [
12] was the FS-RF model with an OA of 77.57%. Among the DBN-based models, the DBN-S and DBN-SVM models were further examined. Their OAs are shown in
Table 13. Statistical tests were also performed and
Table 14 shows the resulting chi-square and
p values. In this situation, if the chi-square value is greater than 12.59, a statistical significance exists at the 95% confidence level (
p < 0.05).
Obviously, the DBN-S and DBN-SVM models significantly outperformed the FS-RF model with OAs of 79.86% and 81.14% and improvements of 2.95% and 4.60%, respectively. Although there was a 1.60% deviation between the DBN-SVM and DBN-S models, no significant difference existed between them.
6. Conclusions
A multimodal and multi-model deep fusion strategy was proposed and tested by conducting FLCC of a CMAL in Wuhan City, China in this study. Three steps were performed. (1) Low-level multimodal features involving spectral–spatial and topographic information were extracted from ZY-3 imagery and fused. (2) These features were entered into a DBN for deep feature learning. (3) The developed deep features were fed to the RF and SVM algorithms for classification. The fused DBN-RF and DBN-SVM models were compared to the DBN-S, RF, SVM, FS-RF, and FS-SVM models. Parameter optimization, model construction, and accuracy assessment were conducted using two sets of data: five groups of training, validation, and test sets with some spatial auto-correlations and a spatially independent test set. Five metrics, i.e., the OA, Kappa coefficient, F1-measure, F1-score, and percentage deviation, were calculated. Generalized McNemar tests were performed to evaluate the performance of the different models. The results showed the following. (1) In the FLCC of the CMAL, the DBN-SVM model achieved an OA of 94.74% ± 0.35% and significantly outperformed the MLA-based models and deep feature-based model of DBN-S. Moreover, the DBN-RF model was significantly better than the MLA-based models and had a predictive power similar to the DBN-S model. (2) In the LCC of the CMAL, the DBN-SVM model achieved an OA of 81.14%, which significantly outperformed the FS-RF model and was slightly better than the DBN-S model. (3) The FLCC and LCC maps had an acceptable visual accuracy.
The following conclusions were drawn from this study. (1) The multimodal and multi-model deep fusion strategy takes advantage of the low-level and multimodal features, unsupervised learning, and the classification abilities of MLAs is effective for FLCC of CMALs. (2) FS is effective for the MLAs and parameter optimization is indispensable for the MLA- and DL-based models. (3) The sampling design should be properly selected and training samples should be added to take full advantage of the effects of the spatial auto-correlation to obtain better predicted maps of large areas. (4) The generalized McNemar test with a relatively large test set is applicable for comparing classification algorithms. Future work will focus on other fusion methods involving different DL algorithms and MLAs for the FLCC of various complex landscapes.