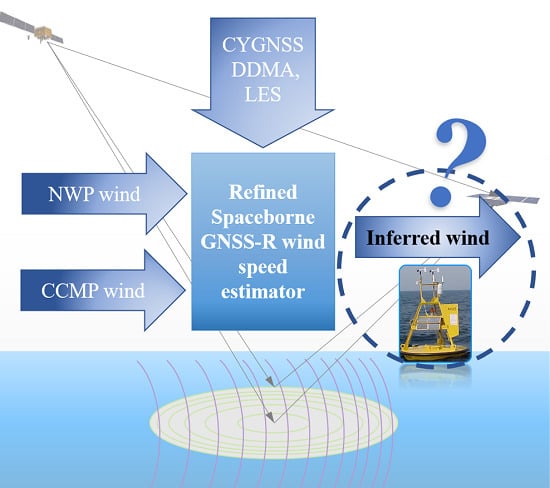
Evaluation of Spaceborne GNSS-R Retrieved Ocean Surface Wind Speed with Multiple Datasets
Abstract
:1. Introduction
2. Theory and Methods
2.1. Bistatic Radar Equation
2.2. Delay-Doppler Map Observables
2.3. Wind Speed Retrieval Algorithm
3. Results and Validation
3.1. Wind Speed Retrieval Based on ERA5 and GDAS
3.2. Wind Speed Retrieval Based on CCMP
3.3. GNSS-R Wind Speed Validation with Buoy Observation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Martineira, M. A Passive Reflectometry and Interferometry System (Paris)—Application to Ocean Altimetry. Esa J. Eur. Space Agency 1993, 17, 331–355. [Google Scholar]
- Katzberg, S.; Garrison, J. Utilizing GPS To Determine Ionospheric Delay over the Ocean; NASA Technical Memorandum 4750; NASA: Greenbelt, MD, USA, 1996.
- Zavorotny, V.; Voronovich, A. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Saïd, F.; Soisuvarn, S.; Jelenak, Z.; Chang, P.S. Performance Assessment of Simulated CYGNSS Measurements in the Tropical Cyclone Environment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4709–4719. [Google Scholar] [CrossRef]
- O’Brien, A.; Johnson, J.T.; IEEE. Comparing the Cygnss Simulator forward Scattering Model with Tds-1 and Cygnss on-Orbit Ddms. In 2017 IEEE International Geoscience and Remote Sensing Symposium; IEEE: New York, NY, USA, 2017; pp. 2657–2658. [Google Scholar]
- Hoover, K.E.; Mecikalski, J.R.; Lang, T.J.; Li, X.; Castillo, T.J.; Chronis, T. Use of an End-to-End-Simulator to Analyze CYGNSS. J. Atmos. Ocean. Technol. 2018, 35, 35–55. [Google Scholar] [CrossRef]
- Garrison, J.L.; Hill, M.I.; Katzberg, S.J. Effect of sea roughness on bistatically scattered range coded signals from the Global Positioning System. Geophys. Res. Lett. 1998, 25, 2257–2260. [Google Scholar] [CrossRef]
- Lin, B.; Katzberg, S.J.; Garrison, J.L.; Wielicki, B.A. Relationship between GPS signals reflected from sea surfaces and surface winds: Modeling results and comparisons with aircraft measurements. J. Geophys. Res. Space Phys. 1999, 104, 20713–20727. [Google Scholar] [CrossRef]
- Lowe, S.T.; LaBrecque, J.L.; Zuffada, C.; Romans, L.J.; Young, L.E.; Hajj, G.A. First spaceborne observation of an Earth-reflected GPS signal. Radio Sci. 2002, 37, 28. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Gommenginger, C.P.; Gleason, S.T.; Srokosz, M.A.; Galdi, C.; Di Bisceglie, M. Analysis of GNSS-R delay-Doppler maps from the UK-DMC satellite over the ocean. Geophys. Res. Lett. 2009, 36, 5. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J.; et al. New Ocean Winds Satellite Mission to Probe Hurricanes and Tropical Convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Lowe, S.; Zuffada, C.; Esterhuizen, S.; Oveisgharan, S. Spaceborne GNSS-R from the SMAP Mission: First Assessment of Polarimetric Scatterometry over Land and Cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar] [CrossRef]
- Wickert, J.; Cardellach, E.; Martin-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F.; et al. GEROS-ISS: GNSS REflectometry, Radio Occultation, and Scatterometry Onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef]
- Gleason, S.; Ruf, C.S.; O’Brien, A.J.; McKague, D.S. The CYGNSS Level 1 Calibration Algorithm and Error Analysis Based on On-Orbit Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 37–49. [Google Scholar] [CrossRef]
- Shah, R.; Garrison, J.L.; Grant, M.S. Demonstration of Bistatic Radar for Ocean Remote Sensing Using Communication Satellite Signals. IEEE Geosci. Remote Sens. Lett. 2012, 9, 619–623. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; De Haan, S. An improved C-band scatterometer ocean geophysical model function: CMOD5. J. Geophys. Res. Space Phys. 2007, 112, 18. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CYGNSS Wind Speed Retrieval Uncertainty. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 87–97. [Google Scholar] [CrossRef]
- Ruf, C.S.; Balasubramaniam, R. Development of the CYGNSS Geophysical Model Function for Wind Speed. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 66–77. [Google Scholar] [CrossRef]
- Lin, W.M.; Portabella, M.; Foti, G.; Stoffelen, A.; Gommenginger, C.; He, Y.J. Toward the Generation of a Wind Geophysical Model Function for Spaceborne GNSS-R. IEEE Trans. Geosci. Remote Sens. 2019, 57, 655–666. [Google Scholar] [CrossRef]
- Gleason, S.; Ruf, C.S.; Clarizia, M.P.; O’Brien, A.J. Calibration and Unwrapping of the Normalized Scattering Cross Section for the Cyclone Global Navigation Satellite System. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2495–2509. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Bayesian Wind Speed Estimation Conditioned on Significant Wave Height for GNSS-R Ocean Observations. J. Atmos. Ocean. Technol. 2017, 34, 1193–1202. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Wind Speed Retrieval Algorithm for the Cyclone Global Navigation Satellite System (CYGNSS) Mission. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4419–4432. [Google Scholar] [CrossRef]
- Huang, F.; Garrison, J.L.; Rodriguez-Alvarez, N.; O’Brien, A.J.; Schoenfeldt, K.M.; Ho, S.C.; Zhang, H. Sequential Processing of GNSS-R Delay-Doppler Maps to Estimate the Ocean Surface Wind Field. Available online: https://ieeexplore.ieee.org/abstract/document/8807371 (accessed on 14 November 2018).
- Liu, Y.; Collett, I.; Morton, Y.J. Application of Neural Network to GNSS-R Wind Speed Retrieval. Available online: https://ieeexplore.ieee.org/abstract/document/8802279 (accessed on 14 November 2018).
- Park, H.; Valencia, E.; Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Ramos-Perez, I.; Camps, A.; IEEE. New Approach to Sea Surface Wind Retrieval from Gnss-R Measurements. In 2011 IEEE International Geoscience and Remote Sensing Symposium; IEEE: New York, NY, USA, 2011; pp. 1469–1472. [Google Scholar] [CrossRef]
- Marchan-Hernandez, J.; Camps, A.; Rodriguez-Alvarez, N.; Valencia, E.; Bosch-Lluis, X.; Ramos-Perez, I. An Efficient Algorithm to the Simulation of Delay–Doppler Maps of Reflected Global Navigation Satellite System Signals. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2733–2740. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. On the Spatial Resolution of GNSS Reflectometry. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1064–1068. [Google Scholar] [CrossRef]
- Hersbach, H.; de Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational global reanalysis: Progress, future directions and synergies with NWP. ERA Rep. Ser. 2018, 27, 65. [Google Scholar]
- National Centers for Environmental Prediction/National Weather Service/NOAA/U.S. Department of Commerce. 2015, Updated Daily. NCEP GDAS/FNL Global Surface Flux Grids. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Available online: https://rda.ucar.edu/datasets/ds084.4/ (accessed on 14 November 2018).
- Wentz, F.J.; Scott, J.; Hoffman, R.; Leidner, M.; Atlas, R.; Ardizzone, J. Cross-Calibrated Multi-Platform Ocean Surface Wind Vector Analysis Product V2, 1987—ongoing. Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. 2016. Available online: https://rda.ucar.edu/datasets/ds745.1/ (accessed on 14 November 2018).
- Thomas, B.R.; Kent, E.C.; Swail, V.R. Methods to homogenize wind speeds from ships and buoys. Int. J. Climatol. 2005, 25, 979–995. [Google Scholar] [CrossRef]
- Jin, S.G.; Feng, G.; Gleason, S. Remote sensing using GNSS signals: current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]














© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Jin, S. Evaluation of Spaceborne GNSS-R Retrieved Ocean Surface Wind Speed with Multiple Datasets. Remote Sens. 2019, 11, 2747. https://doi.org/10.3390/rs11232747
Dong Z, Jin S. Evaluation of Spaceborne GNSS-R Retrieved Ocean Surface Wind Speed with Multiple Datasets. Remote Sensing. 2019; 11(23):2747. https://doi.org/10.3390/rs11232747
Chicago/Turabian StyleDong, Zhounan, and Shuanggen Jin. 2019. "Evaluation of Spaceborne GNSS-R Retrieved Ocean Surface Wind Speed with Multiple Datasets" Remote Sensing 11, no. 23: 2747. https://doi.org/10.3390/rs11232747
APA StyleDong, Z., & Jin, S. (2019). Evaluation of Spaceborne GNSS-R Retrieved Ocean Surface Wind Speed with Multiple Datasets. Remote Sensing, 11(23), 2747. https://doi.org/10.3390/rs11232747