Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images
Abstract
:1. Introduction
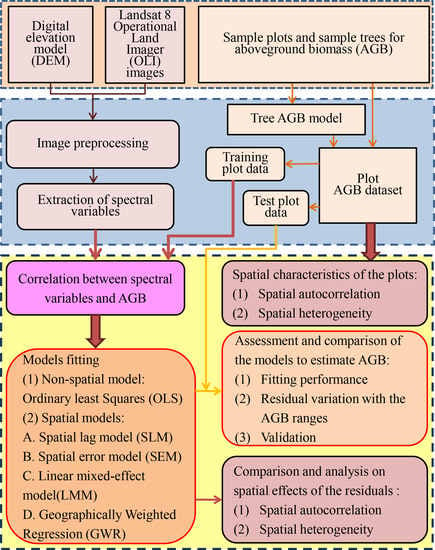
2. Materials and Methods
2.1. Study Area
2.2. Pinus Densata Forests
2.3. Sample Plot Data and Forest Aboveground Biomass
2.4. Collection and Preprocessing of Landsat 8 Images
2.5. Spatial Effect Analysis
2.5.1. Spatial Autocorrelation
2.5.2. Spatial Heterogeneity
2.6. The AGB Estimation using Remote Sensing Data
2.6.1. Ordinary Least Squares (OLS)
2.6.2. Spatial Lag Model (SLM)
2.6.3. Spatial Error Model (SEM)
2.6.4. Linear Mixed-Effects Model (LMM)
2.6.5. Geographically Weighted Regression (GWR)
2.7. Model Evaluation
3. Results
3.1. Spatial Characteristics of Stand Aboveground Biomass
3.1.1. Spatial Autocorrelation
3.1.2. Spatial Heterogeneity
3.2. Model Performance
3.3. Characteristics of Residuals with AGB Classes
3.4. Spatial Effect Analysis for the Models
3.4.1. Spatial Autocorrelation of the Model Residuals
3.4.2. Spatial Heterogeneity of the Model Residuals
4. Discussion
4.1. Spatial Effects
4.2. Model comparison
4.3. Overestimation and Underestimation
4.4. Comparison and Implication of Similar Studies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 4. [Google Scholar] [CrossRef]
- Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent car bon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Chang. Biol. 2015, 21, 1762–1776. [Google Scholar] [CrossRef] [PubMed]
- Goetz, S.J.; Hansen, M.; Houghton, R.A.; Walker, W.; Laporte, N.; Busch, J. Measurement and monitoring needs, capabilities and potential for addressing reduced emissions from deforestation and forest degradation under REDD+. Environ. Res. Lett. 2015, 10, 12. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.E.; Hartig, F.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Stratified aboveground forest biomass estimation by remote sensing data. Int. J. Appl. Earth Obs. 2015, 38, 229–241. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Schroeder, P.; Brown, S.; Mo, J.; Birdsey, R.; Cleszewski, C. Biomass estimation for temperate broadleaf forests of the united states using inventory data. For. Sci. 1997, 43, 424–434. [Google Scholar]
- Rochow, J.J. Estimates of above-ground biomass and primary productivity in a Missouri Forest. J. Ecol. 1974, 62, 567–577. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS J. Photogramm. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Xi, Y. Estimation of forest above-ground biomass by geographically weighted regression and machine learning with Sentinel imagery. Forests 2018, 9, 582. [Google Scholar] [CrossRef]
- Lindeman, R.L. The trophic-dynamic aspect of ecology. Ecology 1942, 23, 399–417. [Google Scholar] [CrossRef]
- Cairns, M.A.; Brown, S.; Helmer, E.H.; Baumgardner, G.A. Root biomass allocation in the world’s upland forests. Oecologia 1997, 111, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest aboveground biomass mapping and estimation across multiple spatial scales using model-based inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Laurin, G.V.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Del Frate, F.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an African tropical forest with LiDAR and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Plank, S. Rapid damage assessment by means of multi-temporal SAR-A comprehensive review and outlook to Sentinel-1. Remote Sens. 2014, 6, 4870–4906. [Google Scholar] [CrossRef]
- Hyde, P.; Nelson, R.; Kimes, D.; Levine, E. Exploring Lidar–Radar synergy—Predicting aboveground biomass in a southwestern ponderosa pine forest using Lidar, Sar and Insar. Remote Sens. Environ. 2007, 106, 28–38. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016, 8, 469. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Montesano, P.M.; Nelson, R.F.; Dubayah, R.O.; Sun, G.; Cook, B.D.; Ranson, K.J.R.; Næsset, E.; Kharuk, V. The uncertainty of biomass estimates from LiDAR and SAR across a boreal forest structure gradient. Remote Sens. Environ. 2014, 154, 398–407. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E.J. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G. Estimation and uncertainty analysis of aboveground forest biomass with Landsat and LiDAR data: Brief overview and case studies. Int. J. For. Res. 2012, 1, 1–16. [Google Scholar]
- Ou, G.; Li, C.; Lv, Y.; Wei, A.; Xiong, H.; Xu, H.; Wang, G. Improving aboveground biomass estimation of Pinus densata forests in Yunnan using Landsat 8 imagery by incorporating age dummy variable and method comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- Diblasi, A.; Bowman, A.W. On the use of the variogram in checking for independence in spatial data. Biometrics 2001, 57, 211. [Google Scholar] [CrossRef]
- Gilbert, B.; Lowell, K. Forest attributes and spatial autocorrelation and interpolation: Effects of alternative sampling schemata in the boreal forest. Landsc. Urban Plan. 1997, 37, 235–244. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, Y.; Li, W.; Gong, H.; Wang, S.; Wang, S. Effects of spatial autocorrelation on individual tree growth model of Picea likiangensis forest in northwest of Yunnan, China. J. Anim. Plant Sci. 2015, 25, 1411–1418. [Google Scholar]
- Kwak, H.; Lee, W.K.; Saborowski, J.; Lee, S.Y.; Won, M.S.; Koo, K.S.; Lee, M.B.; Kim, S.N. Estimating the spatial pattern of human-caused forest fires using a generalized linear mixed model with spatial autocorrelation in south Korea. Int. J. Geogr. Inf. Sci. 2012, 26, 1589–1602. [Google Scholar] [CrossRef]
- Kim, T.J.; Bullock, B.P.; Stape, J.L. Effects of silvicultural treatments on temporal variations of spatial autocorrelation in Eucalyptus plantations in brazil. Forest Ecol. Manag. 2015, 358, 90–97. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, Z.; Guo, L. An evaluation of spatial autocorrelation and heterogeneity in the residuals of six regression models. Forest Sci. 2009, 55, 533–548. [Google Scholar]
- Anselin, L. Lagrange multiplier test diagnostics for spatial dependence and heterogeneity. Geogr. Anal. 1988, 20, 1–17. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Cheng, P.; Davis, C.J. Modeling spatial variation in tree diameter-height relationships. Forest Ecol. Manag. 2004, 189, 317–329. [Google Scholar] [CrossRef]
- Cooper, S.D.; Barmuta, L.; Sarnelle, O.; Kratz, K.; Diehl, S. Quantifying spatial heterogeneity in streams. J. N. Am. Benthol. Soc. 1997, 16, 174–188. [Google Scholar] [CrossRef]
- Legendre, P. Spatial autocorrelation: Trouble or new paradigm? Ecology 1993, 74, 1659. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, Z.; Guo, L. Spatially assessing model errors of four regression techniques for three types of forest stands. Forestry 2008, 81, 209–225. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Shi, H. Local modeling of tree growth by geographically weighted regression. Forest Sci. 2004, 50, 225–244. [Google Scholar]
- Zhang, L.; Gove, J.H.; Heath, L.S. Spatial residual analysis of six modeling techniques. Ecol. Model. 2005, 186, 154–177. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Geary, R.C. The contiguity ratio and statistical mapping. Inc. Stat. 1954, 5, 115–145. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association-LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, L. Local analysis of tree competition and growth. Forest Sci. 2003, 49, 938–955. [Google Scholar]
- Chas-Amil, M.L.; Prestemon, J.P.; Mcclean, C.J.; Touza, J. Human-ignited wildfire patterns and responses to policy shifts. Appl. Geogr. 2015, 56, 164–176. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plan. A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Wang, Q.; Ni, J.; Tenhunen, J. Application of a geographically-weighted regression analysis to estimate net primary production of Chinese forest ecosystems. Glob. Ecol. Biogeogr. 2005, 14, 379–393. [Google Scholar] [CrossRef]
- Roth, R.R. Spatial heterogeneity and bird species diversity. Ecology 1976, 57, 773–782. [Google Scholar] [CrossRef]
- Dutilleul, P. Spatial heterogeneity and the design of ecological field experiments. Ecology 1993, 74, 1646–1658. [Google Scholar] [CrossRef]
- Pickett, S.T.A.; Cadenasso, M.L. Landscape ecology: Spatial heterogeneity in ecological systems. Science 1995, 269, 331–334. [Google Scholar] [CrossRef]
- Carey, A.B. Biocomplexity and restoration of biodiversity in temperate coniferous forest: Inducing spatial heterogeneity with variable-density thinning. Forestry 2003, 76, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Assal, T.J.; Anderson, P.J.; Sibold, J. Spatial and temporal trends of drought effects in a heterogeneous semi-arid forest ecosystem. Forest Ecol. Manag. 2016, 365, 137–151. [Google Scholar] [CrossRef] [Green Version]
- Beckage, B.; Clark, J.S. Seedling survival and growth of three forest tree species: The role of spatial heterogeneity. Ecology 2003, 84, 1849–1861. [Google Scholar] [CrossRef]
- Ngao, J.; Epron, D.; Delpierre, N.; Bréda, N.; Granier, A.; Longdoz, B. Spatial variability of soil CO2, efflux linked to soil parameters and ecosystem characteristics in a temperate beech forest. Agric. Forest Meteorol. 2012, 154, 136–146. [Google Scholar] [CrossRef]
- Ward, J.S.; Parker, G.R.; Ferrandino, F.J. Long-term spatial dynamics in an old-growth deciduous forest. Forest Ecol. Manag. 1996, 83, 189–202. [Google Scholar] [CrossRef]
- Brazhnik, K.; Shugart, H.H. Model sensitivity to spatial resolution and explicit light representation for simulation of boreal forests in complex terrain. Ecol. Model. 2017, 352, 90–107. [Google Scholar] [CrossRef]
- Gundale, M.J.; Metlen, K.L.; Fiedler, C.E.; Deluca, T.H. Nitrogen spatial heterogeneity influences diversity following restoration in a ponderosa pine forest, Montana. Ecol. Appl. 2006, 16, 479–489. [Google Scholar] [CrossRef]
- Clark, P.J.; Evans, F.C. Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Perry, G.L.W.; Miller, B.P.; Enright, N.J. A comparison of methods for the statistical analysis of spatial point patterns in plant ecology. Plant Ecol. 2006, 187, 59–82. [Google Scholar] [CrossRef]
- Fotheringham, A.S. Trends in quantitative methods I: Stressing the local. Prog. Hum. Geogr. 1997, 21, 88–96. [Google Scholar] [CrossRef]
- Fotheringham, A.S. “the problem of spatial autocorrelation” and local spatial statistics. Geogr. Anal. 2009, 41, 398–403. [Google Scholar] [CrossRef]
- Madden, L.V.; Hughes, G.; Ellis, M.A. Spatial heterogeneity of the incidence of grape downy mildew. Phytopathology 1995, 85, 269–275. [Google Scholar] [CrossRef]
- Yang, X.; Han, Y. Spatial heterogeneity of soil nitrogen in six natural secondary forests in mountainous region of northern China. Sci. Soil Water Conserv. 2010, 8, 95–102. [Google Scholar]
- Anselin, L.; Kelejian, H.H. Testing for spatial error autocorrelation in the presence of endogenous regressors. J. Risk Insur. 1997, 20, 153–182. [Google Scholar] [CrossRef] [Green Version]
- Yin, C.; Yuan, M.; Lu, Y.; Huang, Y.; Liu, Y. Effects of urban form on the urban heat island effect based on spatial regression model. Sci. Total Environ. 2018, 634, 696–704. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, F.; Zhu, Y.; Li, F.; Jin, G. Spatial heterogeneity of leaf area index in a temperate old-growth forest: Spatial autocorrelation dominates over biotic and abiotic factors. Sci. Total Environ. 2018, 634, 287–295. [Google Scholar] [CrossRef]
- Guo, L.; Ma, Z.; Zhang, L. Comparison of bandwidth selection in application of geographically weighted regression: A case study. Can. J. Forest Res. 2008, 38, 2526–2534. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, L. Evaluation of parameter estimation methods for fitting spatial regression models. Forest Sci. 2010, 56, 505–514. [Google Scholar]
- Lu, J.; Zhang, L. Modeling and prediction of tree height diameter relationships using spatial autoregressive models. For. Sci. 2011, 57, 252–264. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, L. Geographically local linear mixed models for tree height-diameter relationship. Forest Sci. 2012, 58, 75–84. [Google Scholar] [CrossRef]
- Imran, M.; Zuritamilla, R.; Stein, A. Modeling crop yield in west-African rainfed agriculture using global and local spatial regression. Agron. J. 2013, 105, 1177–1188. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Propastin, P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. Int. J. Appl. Earth Obs. 2012, 18, 82–90. [Google Scholar] [CrossRef]
- Compilation Committee of Yunnan Forest. Yunnan Forest; Yunnan Science and Technology Press: Kunming, China; China Forestry Publishing House: Beijing, China, 1986. [Google Scholar]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Reese, H.; Olsson, H. C-correction of optical satellite data over alpine vegetation areas: A comparison of sampling strategies for determining the empirical c-parameter. Remote Sens. Environ. 2011, 115, 1387–1400. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Fan, J.; Fu, X.; Fan, H. Analysis and comparison test on C-correction strategies and their scale effects with TM images in rugged mountainous terrain. J. Geo-Inf. Sci. 2014, 16, 134–141. [Google Scholar]
- Wang, G.; Zhang, M.; Gertner, G.Z.; Oyana, T.; McRoberts, R.E.; Ge, H. Uncertainties of mapping forest carbon due to plot locations using national forest inventory plot and remotely sensed data. Scand. J. For. Res. 2011, 26, 360–373. [Google Scholar] [CrossRef]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Boots, B. Local measures of spatial association. Eco. Sci. 2002, 9, 168–176. [Google Scholar] [CrossRef]
- Zhang, L.; Gove, J.H. Spatial assessment of model errors from four regression techniques. For. Sci. 2005, 51, 334–346. [Google Scholar]
- Liu, C.; Zhang, L.; Li, F.; Jin, X. Spatial modeling of the carbon stock of forest trees in Heilongjiang Province, China. J. For. Res. 2014, 25, 269–280. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications, 3rd ed.; Springer: New York, NY, USA, 2003; p. 387. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sens. Environ. 2006, 103, 81–96. [Google Scholar] [CrossRef]
- Sawada, M. Rookcase: An excel 97/2000 visual basic (VB) add-in for exploring global and local spatial autocorrelation. Bull. Ecol. Soc. Am. 1999, 80, 231–234. [Google Scholar]
- Foody, G.M. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI–rainfall relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Foody, G.M. Spatial nonstationarity and scale-dependency in the relationship between species richness and environmental determinants for the sub-Saharan endemic avifauna. Glob. Ecol. Biogeogr. 2004, 13, 315–320. [Google Scholar] [CrossRef]
- Bickford, S.A.; Laffan, S.W. Multi-extent analysis of the relationship between pteridophyte species richness and climate. Glob. Ecol. Biogeogr. 2006, 15, 588–601. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. Geoda: An introduction to spatial data analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An introduction to spatial data analysis. In Handbook of Applied Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty; John Wiley & Sons: New York, NY, USA, 1999; p. 695. [Google Scholar]
- Myers, D.E. Statistical models for multiple-scaled analysis. In Scale in Remote Sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1997; pp. 273–293. [Google Scholar]
- Song, W.; Jia, H.; Li, Z.; Tang, D. Using geographical semi-variogram method to quantify the difference between NO2 and PM 2.5 spatial distribution characteristics in urban areas. Sci. Total Environ. 2018, 631–632, 688–694. [Google Scholar] [CrossRef]
- Farber, S.; Páez, A. A systematic investigation of cross-validation in GWR model estimation: Empirical analysis and Monte Carlo simulations. J. Geogr. Syst. 2007, 9, 371–396. [Google Scholar] [CrossRef]
- Kupfer, J.A.; Farris, C.A. Incorporating spatial non-stationarity of regression coefficients into predictive vegetation models. Landsc. Ecol. 2007, 22, 837–852. [Google Scholar] [CrossRef]
- Lu, B.; Yang, W.; Ge, Y.; Harris, P. Improvements to the calibration of a geographically weighted regression with parameter-specific distance metrics and bandwidths. Comput. Environ. Urban Syst. 2018, 71, 41–57. [Google Scholar] [CrossRef]
- Lou, M.; Zhang, H.; Lei, X.; Li, C.; Zang, H. Spatial autoregressive models for stand top and stand mean height relationship in mixed Quercus mongolica broadleaved natural stands of northeast China. Forests 2016, 7, 43. [Google Scholar] [CrossRef] [Green Version]
- Littell, R.C.; Milliken, G.A.; Wolfinger, R.D.; Schabenberger, O.; Institute, S. Sas for Mixed Models; SAS Institute, Inc.: Cary, NC, USA, 2006; p. 814. [Google Scholar]
- Chen, W.; Chen, J.; Liu, J.; Cihlar, J. Approaches for reducing uncertainties in regional forest carbon balance. Glob. Biogeochem. Cycles 2000, 14, 827–838. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; BrondíZio, E.; Moran, E. Relationships between forest stand parameters and Landsat TM spectral responses in the Brazilian Amazon basin. For. Ecol. Manag. 2004, 198, 149–167. [Google Scholar] [CrossRef]
- Mascaro, J.; Detto, M.; Asner, G.P.; Muller-Landau, H.C. Evaluating uncertainty in mapping forest carbon with airborne lidar. Remote Sens. Environ. 2011, 115, 3770–3774. [Google Scholar] [CrossRef]
- Gregoryp, A.; Flint, H.R.; Timothya, V.; Davide, K.; Ty, K.B. Environmental and biotic controls over aboveground biomass throughout a tropical rain forest. Ecosystems 2009, 12, 261–278. [Google Scholar]
- Nabuurs, G.J.; Van, P.B.; Knippers, T.S.; Gmj, M. Comparison of uncertainties in carbon sequestration estimates for a tropical and a temperate forest. For. Ecol. Manag. 2008, 256, 237–245. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. ISPRS J. Photogramm. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Yue, C.R. Forest Biomass Estimation in Shangri-La County Based on Remote Sensing; Beijing Forestry University: Beijing, China, 2011. [Google Scholar]
- Sun, X.L. Biomass Estimation Model of Pinus Densata Forests in Shangri-la City Based on Landsat 8- OLI by Remote Sensing; Southwest Forestry University: Kunming, China, 2016. [Google Scholar]










| Variables | Minimum | Maximum | Mean | Standard Deviation | |
|---|---|---|---|---|---|
| Fitting dataset (n = 117) | Hm (m) | 2.2 | 21.7 | 10.3 | 3.5 |
| Dg (cm) | 2.9 | 39.6 | 15.1 | 5.0 | |
| AGB (Mg/ha) | 2.1 | 251.5 | 117.6 | 58.6 | |
| Test dataset (n = 30) | Hm (m) | 3.1 | 24.3 | 9.6 | 4.5 |
| Dg (cm) | 5.0 | 41.3 | 13.7 | 7.1 | |
| AGB (Mg/ha) | 11.1 | 344.4 | 96.1 | 60.4 | |
| All dataset (n = 147) | Hm (m) | 2.2 | 24.3 | 10.12 | 3.7 |
| Dg (cm) | 2.9 | 41.3 | 14.8 | 5.5 | |
| AGB (Mg/ha) | 2.1 | 344.4 | 113.2 | 59.4 | |
| Variable | Minimum | Maximum | Mean | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| AGB | −0.0204 | 0.0273 | 0.0008 | 0.0004 | 0.7139 | 8.9277 |
| Z-Score | |Z| < 1.96 | 2.58 > |Z| ≥ 1.96 | |Z| ≥ 2.58 | Total | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| −2.58 < Z ≤ −1.96 | 1.96 < Z ≤ 2.58 | ≤−2.58 | ≥2.58 | |||||||
| Types | NS | LH | HL | LL | HH | LH | HL | LL | HH | |
| Number | 127 | 3 | 0 | 0 | 4 | 0 | 0 | 4 | 9 | 147 |
| Percentage | 86.39 | 2.04 | 0 | 0 | 2.72 | 0 | 0 | 2.72 | 6.12 | 100 |
| Models | Fitting (n = 117) | Test (n = 30) | |||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (Mg/ha) | AIC | ME (Mg/ha) | MAE (Mg/ha) | MRE (%) | MARE (%) | |
| OLS | 0.239 | 51.137 | 1263.701 | −25.199 | 50.063 | −18.545 | 41.094 |
| SEM | 0.266 | 50.219 | 1258.720 | −24.125 | 48.804 | −18.578 | 40.452 |
| SLM | 0.282 | 49.672 | 1258.250 | −24.388 | 51.064 | −16.590 | 44.110 |
| LMM | 0.361 | 46.845 | 1218.107 | −22.932 | 48.385 | −12.495 | 44.908 |
| GWR | 0.665 | 34.507 | 1199.341 | −18.923 | 45.568 | −9.070 | 40.091 |
| Regression Coefficients | Variables | OLS | SEM | SLM | LMM | GWR |
|---|---|---|---|---|---|---|
| Constant | −39.464 (45.874) | −24.041 (44.943) | −77.359 (46.625) | −22.533 (44.182) | −52.270 (−549.500~148.900) | |
| CC3_1 | 29.973 (14.932) | 27.917 (14.392) | 27.488 (14.214) | 26.689 (14.234) | 28.700 (−120.900~114.800) | |
| SM7_1 | 170.780 (46.626) | 151.130 (49.912) | 154.079 (44.471) | 145.064 (44.299) | 167.200 (−1.164~589.800) | |
| DI7_1 | 213.320 (74.473) | 188.358 (71.714) | 191.809 (70.938) | 175.979 (71.224) | 178.800 (−72.470~920.900) | |
| CC7_3 | −44.167 (17.499) | −37.412 (16.724) | −39.096 (16.642) | −33.699 (16.685) | −33.640 (−121.000~109.100) | |
| Spatial parameters | = 0.432 (0.199) | = 0.444 (0.174) | ||||
| Models | <40 (Mg/ha) | 40–80 (Mg/ha) | 80–120 (Mg/ha) | 120–160 (Mg/ha) | 160–200 (Mg/ha) | >200 (Mg/ha) | Overall | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | μ | σ | |
| OLS | 65.25 | 8.17 | 46.57 | 5.00 | 11.14 | 4.95 | −23.47 | 5.68 | −38.57 | 5.14 | −86.68 | 7.72 | 0.02 | 4.73 |
| SLM | 65.12 | 8.13 | 43.25 | 5.11 | 9.66 | 4.69 | −22.51 | 5.34 | −39.00 | 5.14 | −86.30 | 7.25 | −0.83 | 4.62 |
| SEM | 66.88 | 7.26 | 47.06 | 4.63 | 10.61 | 4.38 | −24.65 | 5.18 | −41.82 | 4.68 | −89.71 | 6.97 | −0.87 | 4.74 |
| LMM | 67.21 | 9.35 | 39.16 | 4.55 | 4.35 | 5.23 | −22.82 | 5.26 | −29.65 | 6.53 | −71.54 | 5.77 | 0.02 | 4.33 |
| GWR | 26.91 | 7.62 | 31.96 | 4.68 | 3.08 | 3.99 | −10.67 | 5.60 | −16.58 | 7.70 | −42.88 | 7.59 | 1.04 | 3.13 |
| Models | Minimum | Maximum | Mean | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| OLS | −121.548 | 136.502 | −1.71 × 10−7 | 51.137 | 0.157 | −0.404 |
| SLM | −127.740 | 128.666 | 8.55 × 10−8 | 49.672 | 0.100 | −0.344 |
| SEM | −122.801 | 130.236 | −1.71 × 10−7 | 50.219 | 0.126 | −0.421 |
| LMM | −133.338 | 109.608 | 3.77 × 10−14 | 46.845 | −0.103 | −0.237 |
| GWR | −80.815 | 87.538 | −0.993 | 34.507 | 0.212 | 0.256 |
| Models | Moran’s I | Z Score |
|---|---|---|
| OLS | 0.151 | 4.296 |
| SEM | 0.096 | 2.809 |
| SLM | 0.064 | 1.945 |
| LMM | −0.030 | −0.575 |
| GWR | −0.048 | −1.075 |
| Models | Minimum | Maximum | Mean | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| OLS | −25.645 | 21.068 | 1.547 | 6.244 | −0.464 | 4.874 |
| SEM | −21.307 | 15.010 | 0.651 | 5.029 | −1.102 | 6.772 |
| SLM | −23.110 | 17.765 | 0.981 | 5.627 | −0.940 | 6.263 |
| LMM | −11.632 | 5.349 | −0.307 | 2.565 | −1.731 | 6.306 |
| GWR | −15.016 | 7.220 | −0.496 | 2.586 | −2.246 | 11.675 |
| Z Score | |Z| < 1.96 | 2.58 > |Z| ≥ 1.96 | |Z| ≥ 2.58 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| −2.58 < Z ≤ −1.96 | 1.96 < Z ≤ 2.58 | ≤−2.58 | ≥2.58 | ||||||
| Types | NS | LH | HL | LL | HH | LH | HL | LL | HH |
| OLS | 98 (83.76) | 1 (0.85) | 0 (0.00) | 0 (0.00) | 3 (2.56) | 2 (1.71) | 0 (0.00) | 3 (2.56) | 10 (8.55) |
| SEM | 99 (84.62) | 1 (0.85) | 0 (0.00) | 3 (2.56) | 4 (3.42) | 3 (2.56) | 0 (0.00) | 0 (0.00) | 7 (5.98) |
| SLM | 103 (88.03) | 0 (0.00) | 0 (0.00) | 3 (2.56) | 3 (2.56) | 3 (2.56) | 0 (0.00) | 0 (0.00) | 5 (4.27) |
| LMM | 114 (97.44) | 0 (0.00) | 0 (0.00) | 1 (0.85) | 0 (0.00) | 1 (0.85) | 0 (0.00) | 0 (0.00) | 1 (0.85) |
| GWR | 112 (95.73) | 3 (2.56) | 0 (0.00) | 0 (0.00) | 0 (0.00) | 0 (0.00) | 1 (0.85) | 1 (0.85) | 0 (0.00) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, G.; Lv, Y.; Xu, H.; Wang, G. Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images. Remote Sens. 2019, 11, 2750. https://doi.org/10.3390/rs11232750
Ou G, Lv Y, Xu H, Wang G. Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images. Remote Sensing. 2019; 11(23):2750. https://doi.org/10.3390/rs11232750
Chicago/Turabian StyleOu, Guanglong, Yanyu Lv, Hui Xu, and Guangxing Wang. 2019. "Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images" Remote Sensing 11, no. 23: 2750. https://doi.org/10.3390/rs11232750
APA StyleOu, G., Lv, Y., Xu, H., & Wang, G. (2019). Improving Forest Aboveground Biomass Estimation of Pinus densata Forest in Yunnan of Southwest China by Spatial Regression using Landsat 8 Images. Remote Sensing, 11(23), 2750. https://doi.org/10.3390/rs11232750