Optimal Assimilation of Daytime SST Retrievals from SEVIRI in a Regional Ocean Prediction System
Abstract
:1. Introduction
2. Data and Methods
3. SST Data Assimilation
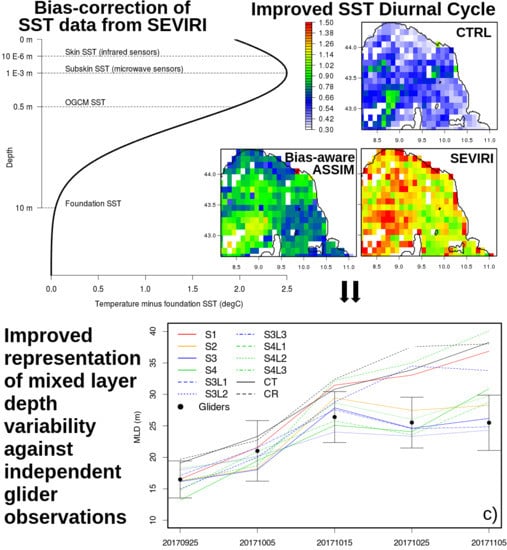
3.1. Skin SST Prognostic Scheme
3.2. SST Bias Correction Scheme
3.3. SST Vertical Localization
4. Experimental Setup and Results
4.1. Configuration of the Experiments
4.2. Analysis Increments, Mean Ocean State, and Diurnal Variability
4.3. Validation against Independent Data
4.3.1. Validation against Glider Data
4.3.2. Validation against Mooring and Drifter Data
5. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Le Traon, P.Y. Satellites and Operational Oceanography. In Operational Oceanography in the 21st Century; Schiller, A., Brassington, G.B., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 29–54. [Google Scholar] [CrossRef]
- Oke, P.R.; Larnicol, G.; Jones, E.M.; Kourafalou, V.; Sperrevik, A.K.; Carse, F.; Tanajura, C.A.S.; Mourre, B.; Tonani, M.; Brassington, G.B.; et al. Assessing the impact of observations on ocean forecasts and reanalyses: Part 2, Regional applications. J. Oper. Oceanogr. 2015, 8, s63–s79. [Google Scholar] [CrossRef]
- Legler, D.M.; Freeland, H.J.; Lumpkin, R.; Ball, G.; McPhaden, M.J.; North, S.; Crowley, R.; Goni, G.J.; Send, U.; Merrifield, M.A. The current status of the real-time in situ Global Ocean Observing System for operational oceanography. J. Oper. Oceanogr. 2015, 8, s189–s200. [Google Scholar] [CrossRef]
- Miyazawa, Y.; Varlamov, S.M.; Miyama, T.; Guo, X.; Hihara, T.; Kiyomatsu, K.; Kachi, M.; Kurihara, Y.; Murakami, H. Assimilation of high-resolution sea surface temperature data into an operational nowcast/forecast system around Japan using a multi-scale three-dimensional variational scheme. Ocean Dyn. 2017, 67, 713–728. [Google Scholar] [CrossRef]
- Chen, Y.L.; Yan, C.X.; Zhu, J. Assimilation of sea surface temperature in a global Hybrid Coordinate. Ocean Model. Adv. Atmos. Sci. 2018, 35, 1291–1304. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, W. Assimilating high-resolution sea surface temperature data improves the ocean forecast potential in the Baltic Sea. Ocean Sci. 2018, 14, 525–541. [Google Scholar] [CrossRef]
- Helber, R.W.; Barron, C.N.; Carnes, M.R.; Zingarelli, R.A. Evaluating the sonic layer depth relative to themixed layer depth. J. Geophys. Res. 2008, 113, C07033. [Google Scholar] [CrossRef]
- Waters, J.; Lea, D.J.; Martin, M.J.; Mirouze, I.; Weaver, A.; While, J. Implementing a variational data assimilation system in an operational 1/4 degree global ocean model. Q. J. R. Meteorol. Soc. 2015, 141, 333–349. [Google Scholar] [CrossRef]
- Storto, A.; Masina, S. C-GLORSv5: An improved multipurpose global ocean eddy-permitting physical reanalysis. Earth Syst. Sci. Data 2016, 8, 679–696. [Google Scholar] [CrossRef]
- Marullo, S.; Santoleri, R.; Ciani, D.; le Borgne, P.; Péré, S.; Pinardi, N.; Tonani, M.; Nardone, G. Combining model and geostationary satellite data to reconstruct hourly SST field over the Mediterranean Sea. Remote Sens. Environ. 2014, 146. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Donlon, C.J.; Stuart-Menteth, A.; Wentz, F.J. Diurnal signals in satellite sea surface temperature measurements. Geophys. Res. Lett. 2003, 30, 1140. [Google Scholar] [CrossRef]
- Marullo, S.; Minnett, P.J.; Santoleri, R.; Tonani, M. The diurnal cycle of sea-surface temperature and estimation of the heat budget of the Mediterranean Sea. J. Geophys. Res. Ocean. 2016, 121, 8351–8367. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- GHRSST. Available online: https://www.ghrsst.org/ghrsst-data-services/products (accessed on 19 November 2019).
- While, J.; Mao, C.; Martin, M.J.; Roberts-Jones, J.; Sykes, P.A.; Good, S.A.; McLaren, A.J. An operational analysis system for the global diurnal cycle of sea surface temperature: Implementation and validation. Q. J. R. Meteorol. Soc. 2017, 143, 1787–1803. [Google Scholar] [CrossRef]
- Akella, S.; Todling, R.; Suarez, M. Assimilation for skin SST in the NASA GEOS atmospheric data assimilation system. Q. J. R. Meteorol. Soc. 2017, 143, 1032–1046. [Google Scholar] [CrossRef] [PubMed]
- Gentemann, C.L.; Akella, S. Evaluation of NASA GEOS-ADAS modeled diurnal warming through comparisons to SEVIRI and AMSR2 SST observations. J. Geophys. Res. Ocean. 2018, 123, 1364–1375. [Google Scholar] [CrossRef]
- Korres, G.; Denaxa, D.; Jansen, E.; Mirouze, I.; Pimentel, S.; Tse, W.H.; Storto, A. Assimilation of SST data in the POSEIDON system using the SOSSTA statistical-dynamical observation operator. Ocean Sci. Discuss. 2019. [Google Scholar] [CrossRef]
- Jansen, E.; Pimentel, S.; Tse, W.H.; Denaxa, D.; Korres, G.; Mirouze, I.; Storto, A. Using Canonical Correlation Analysis to produce dynamically-based highly-efficient statistical observation operators. Ocean Sci. 2019, 1023–1032. [Google Scholar] [CrossRef]
- Storto, A.; Oddo, P.; Cozzani, E.; Coelho, E.F. Introducing along-track error correlations for altimetry data in a regional ocean prediction system. J. Atmos. Ocean. Technol. 2019. [Google Scholar] [CrossRef]
- Oddo, P.; Storto, A.; Dobricic, S.; Russo, A.; Lewis, C.; Onken, R.; Coelho, E. A hybrid variational-ensemble data assimilation scheme with systematic error correction for limited-area ocean models. Ocean Sci. 2016, 12, 1137–1153. [Google Scholar] [CrossRef]
- Storto, A.; Oddo, P.; Cipollone, A.; Mirouze, I.; Lemieux, B. Extending an oceanographic variational scheme to allow for affordable hybrid and four-dimensional data assimilation. Ocean Model. 2018, 128, 67–86. [Google Scholar] [CrossRef]
- Storto, A.; Falchetti, S.; Oddo, P.; Jiang, Y.M.; Tesei, A. Assessing the Impact of Different Ocean Analysis Schemes On Oceanic and Underwater Acoustic Predictions. J. Geophys. Res. Ocean. 2019. in review. [Google Scholar]
- Dobricic, S.; Pinardi, N. An oceanographic three-dimensional assimilation scheme. Ocean Model. 2008, 22, 89–105. [Google Scholar] [CrossRef]
- Madec, G.; the NEMO team. NEMO Ocean Engine; Note du Pole de modélisation; Institut Pierre-Simon Laplace: Paris, France, 2012. [Google Scholar]
- Large, W.G.; Yeager, S. Diurnal to Decadal Global Forcing for Ocean and Sea-Ice Models: The Data Sets And Flux Climatologies; NCAR Technical Note, NCAR/TN-460+STR; CGD Division of the National Center for Atmospheric Research: Boulder, CO, USA, 2004. [Google Scholar]
- Oddo, P.; Bonaduce, A.; Pinardi, N.; Guarnieri, A. Sensitivity of the Mediterranean sea level to atmospheric pressure and free surface elevation numerical formulation in NEMO. Geosci. Model Dev. 2014, 7, 3001–3015. [Google Scholar] [CrossRef]
- Weatherall, P.; Marks, K.M.; Jakobsson, M.; Schmitt, T.; Tani, S.; Arndt, J.E.; Rovere, M.; Chayes, D.; Ferrini, V.; Wigley, R. A new digital bathymetric model of the world’s oceans. Earth Space Sci. 2015, 2, 331–345. [Google Scholar] [CrossRef]
- Barnier, B.; Madec, G.; Penduff, T.; Molines, J.M.; Treguier, A.M.; le Sommer, J.; Beckmann, A.; Biastoch, A.; Boning, C.; Dengg, J.; et al. Impact of partial steps and momentum advection schemes in a global circulation model at eddy permitting resolution. Ocean Dyn. 2006, 56, 543–567. [Google Scholar] [CrossRef]
- Lengaigne, M.; Menkes, C.; Aumont, O.; Gorgues, T.; Bopp, L.; Madec, J.M.A.G. Biophysical feedbacks on the tropical pacific climate in a coupled general circulation model. Clim. Dyn. 2007, 28, 503–516. [Google Scholar] [CrossRef]
- Volpe, G.; Colella, S.; Forneris, V.; Tronconi, C.; Santoleri, R. The Mediterranean Ocean Colour Observing System—System development and product validation. Ocean Sci. 2012, 8, 869–883. [Google Scholar] [CrossRef]
- Bloom, S.C.; Takacs, L.L.; da Silva, A.M.; Ledvina, D. Data Assimilation Using Incremental Analysis Updates. Mon. Weather Rev. 1996, 124, 1256–1271. [Google Scholar] [CrossRef]
- Derrien, M.; Le Gléau, H. MSG/SEVIRI cloud mask and type from SAFNWC. Int. J. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Marsouin, A.; Roquet, H. Sea surface temperature from a geostationary satellite by optimal estimation. Remote Sens. Environ. 2009, 113, 445–457. [Google Scholar] [CrossRef]
- Marullo, S.; Santoleri, R.; Banzon, V.; Evans, R.H.; Guarracino, M. A diurnal-cycle resolving sea surface temperature product for the tropical Atlantic. J. Geophys. Res. 2010, 115, C05011. [Google Scholar] [CrossRef]
- Le Borgne, P.; Roquet, H.; Merchant, C. Estimation of sea Surface Temperature from the SEVIRI, improved using numerical weather prediction. Remote Sens. Environ. 2011, 115, 55–65. [Google Scholar] [CrossRef]
- OSI-SAF. Geostationary Sea Surface Temperature Product User Manual, Document SAF/OSI/CDOP3/MF/TEC/MA/181. Prepared by Meteo-France. 2018. Available online: http://www.osi-saf.org/lml/doc/osisaf_cdop2_ss1_pum_geo_sst.pdf (accessed on 25 February 2019).
- Donlon, C.J.; Minnett, P.J.; Gentemann, C.; Nightingale, T.J.; Barton, I.J.; Ward, B.; Murray, M.J. Toward improved and validation of satellite and sea surface and skin temperature and measurements and for climate and research. J. Clim. 2002, 15, 353–359. [Google Scholar] [CrossRef] [Green Version]
- Merchant, C.J.; Filipiak, M.J.; le Borgne, P.; Roquet, H.; Autret, E.; Piollé, J.F.; Lavender, S. Diurnal warm-layer events in the western Mediterranean and European shelf seas. Geophys. Res. Lett. 2008, 35, L04601. [Google Scholar] [CrossRef] [Green Version]
- Karagali, I.; Høyer, J.L. Characterisation and quantification of regional diurnal SST cycles from SEVIRI. Ocean Sci. 2014, 10, 745–758. [Google Scholar] [CrossRef] [Green Version]
- Takaya, Y.; Bidlot, J.R.; Beljaars, A.C.M.; Janssen, P.A.E.M. Refinements to a prognostic scheme of sea surface skin temperature. J. Geophys. Res. 2010, 115, C06009. [Google Scholar] [CrossRef] [Green Version]
- Artale, V.; Iudicone, D.; Santoleri, R.; Rupolo, V.; Marullo, S.; D’Ortenzio, F. Role of surface fluxes in ocean general circulation models using satellite sea surface temperature: Validation of and sensitivity to the forcing frequency of the Mediterranean thermohaline circulation. J. Geophys. Res. Ocean. 2002, 107, 1978–2012. [Google Scholar] [CrossRef]
- Saunders, P.M. The temperature at the ocean-air interface. J. Atmos. Sci. 1967, 24, 269–273. [Google Scholar] [CrossRef] [Green Version]
- Zeng, X.; Beljaars, A. A prognostic scheme of sea surface skin temperature for modeling and data assimilation. Geophys. Res. Lett. 2005, 32, L14605. [Google Scholar] [CrossRef] [Green Version]
- Tu, C.; Tsuang, B. Cool-skin simulation by a one-column ocean model. Geophys. Res. Lett. 2005, 32, L22602. [Google Scholar] [CrossRef] [Green Version]
- Harris, B.A.; Kelly, G. A satellite radiance-bias correction scheme for data assimilation. Q. J. R. Meteorol. Soc. 2001, 127, 1453–1468. [Google Scholar] [CrossRef]
- Storto, A.; Randriamampianina, R. A New Bias Correction Scheme for Assimilating GPS Zenith Tropospheric Delay Estimates. Idojaras 2010, 114, 237–250. [Google Scholar]
- Auligné, T.; McNally, A.P.; Dee, D.P. Adaptive bias correction for satellite data in a numerical weather prediction system. Q. J. R. Meteorol. Soc. 2007, 133, 631–642. [Google Scholar] [CrossRef]
- Eyre, J.R. Observation bias correction schemes in data assimilation systems: A theoretical study of some of their properties. Q. J. R. Meteorol. Soc. 2016, 142, 2284–2291. [Google Scholar] [CrossRef]
- Schroeder, L.D.; Sjoquist, D.L.; Stephan, P.E. Understanding Regression Analysis; Sage Publications: Saunders Oaks, CA, USA, 1986; pp. 31–32. [Google Scholar]
- Auligné, T. An objective approach to modelling biases in satellite radiances: Application to AIRS and AMSU-A. Q. J. R. Meteorol. Soc. 2007, 133, 1789–1801. [Google Scholar] [CrossRef]
- Le Borgne, P.; Marsouin, A.; Orain, F.; Roquet, H. Operational sea surface temperature bias adjustment using AATSR data. Remote Sens. Environ. 2012, 116, 93–106. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; Wiley-Interscience: Hoboken, NJ, USA, 1998; ISBN 978-0-471-17082-2. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J. Applied Linear Regression Models, 4th ed.; McGraw-Hill Irwin: New York, NY, USA, 2004; ISBN 978-0073014661. [Google Scholar]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Karatzoglou, A.; Smola, A.; Kurt, H.; Zeileis, A. Kernlab—An S4 Package for Kernel Methods in R. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Buehner, M. Ensemble-derived stationary and flow-dependent background-error covariances: Evaluation in a quasi-operational NWP setting. Q. J. R. Meteorol. Soc. 2005, 131, 1013–1043. [Google Scholar] [CrossRef]
- Wang, X.; Snyder, C.; Hamill, T. On the theoretical equivalence of differently proposed ensemble-3DVAR hybrid analysis schemes. Mon. Weather Rev. 2007, 135, 222–227. [Google Scholar] [CrossRef]
- Oke, P.R.; Sakov, P. Representation error of oceanic observations for data assimilation. J. Atmos. Oceanic Technol. 2008, 25, 1004–1017. [Google Scholar] [CrossRef] [Green Version]
- Oke, P.R.; Brassington, G.B.; Griffin, D.A.; Schiller, A. The Bluelink ocean data assimilation system (BODAS). Ocean Model. 2008, 21, 46–70. [Google Scholar] [CrossRef] [Green Version]
- Nardelli, B.B.; Tronconi, C.; Pisano, A.; Santoleri, R. High and Ultra-High resolution processing of satellite Sea Surface Temperature data over Southern European Seas in the framework of MyOcean project. Remote Sens. Environ. 2013, 129, 1–16. [Google Scholar] [CrossRef]
- Courtier, P. Variational methods. J. Meteorol. Soc. Jpn. 1997, 75, 211–218. [Google Scholar] [CrossRef] [Green Version]
- Storto, A. Variational quality control of hydrographic profile data with non-Gaussian errors for global ocean variational data assimilation systems. Ocean Model. 2016, 104, 226–241. [Google Scholar] [CrossRef]
- Fofonoff, N.P.; Millard, R.C. Algorithms for Computation of Fundamental Properties of Seawater. UNESCO Technical Papers in Marine Science, 1983, 44, Paris. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000059832 (accessed on 23 November 2019).
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
















| Experiment | SST Assimilation | SST Data | Method | Localization |
|---|---|---|---|---|
| CT | NO | - | - | - |
| CR | Nudging | L4 (Foundation) | 1st Level | - |
| S1 | Hybrid 3DVAR | Night-time SEVIRI | 1st Level | NO |
| S2 | Hybrid 3DVAR | All-day SEVIRI | 1st Level | NO |
| S3 | Hybrid 3DVAR | All-day SEVIRI | 1st Level + bias correction | NO |
| S4 | Hybrid 3DVAR | All-day SEVIRI | Warm layer skin SST | NO |
| S3L1 | Hybrid 3DVAR | All-day SEVIRI | 1st Level + bias correction | MLD (L1) |
| S3L2 | Hybrid 3DVAR | All-day SEVIRI | 1st Level + bias correction | DEN1 (L2) |
| S3L3 | Hybrid 3DVAR | All-day SEVIRI | 1st Level + bias correction | DEN2 (L3) |
| S4L1 | Hybrid 3DVAR | All-day SEVIRI | Warm layer skin SST | MLD (L1) |
| S4L2 | Hybrid 3DVAR | All-day SEVIRI | Warm layer skin SST | DEN1 (L2) |
| S4L3 | Hybrid 3DVAR | All-day SEVIRI | Warm layer skin SST | DEN2 (L3) |
| Experiment | MLD Bias (m) | MLD RMSE (m) |
|---|---|---|
| CT | 6.9 | 11.2 |
| CR | 6.7 | 11.4 (−1.8%) |
| S1 | 4.4 | 10.9 (2.7%) |
| S2 | −0.3 | 9.5 (15.2%) |
| S3 | 0.2 | 8.9 (20.5%) |
| S4 | 0.3 | 9.0 (19.6%) |
| S3L1 | 5.0 | 10.5 (6.2%) |
| S3L2 | −1.6 | 9.0 (19.6%) |
| S3L3 | −0.1 | 8.6 (23.2%) |
| S4L1 | 6.6 | 11.2 (0.0%) |
| S4L2 | 0.4 | 9.9 (11.6%) |
| S4L3 | −0.4 | 8.8 (21.4%) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Storto, A.; Oddo, P. Optimal Assimilation of Daytime SST Retrievals from SEVIRI in a Regional Ocean Prediction System. Remote Sens. 2019, 11, 2776. https://doi.org/10.3390/rs11232776
Storto A, Oddo P. Optimal Assimilation of Daytime SST Retrievals from SEVIRI in a Regional Ocean Prediction System. Remote Sensing. 2019; 11(23):2776. https://doi.org/10.3390/rs11232776
Chicago/Turabian StyleStorto, Andrea, and Paolo Oddo. 2019. "Optimal Assimilation of Daytime SST Retrievals from SEVIRI in a Regional Ocean Prediction System" Remote Sensing 11, no. 23: 2776. https://doi.org/10.3390/rs11232776
APA StyleStorto, A., & Oddo, P. (2019). Optimal Assimilation of Daytime SST Retrievals from SEVIRI in a Regional Ocean Prediction System. Remote Sensing, 11(23), 2776. https://doi.org/10.3390/rs11232776