1. Introduction
Land cover and land use (LCLU) classification is the fundamental task in remote sensing image interpretation, with the goal of assigning a category label to each pixel of an image [
1]. It provides the opportunity to monitor and analyze the evolution of global earth and key regions, and has spawned many new applications, e.g., precision agriculture [
1], population density estimation [
2], location information service [
3]. Among these applications, automatic building extraction with optical remote sensing (ORS) images is one of the most popular research directions [
4,
5,
6,
7], owing to its convenience and feasibility.
As the resolution of ORS images has reached the decimeter level, more and more elaborate structure, texture and spectral information of buildings has become available. Meanwhile, the increasing intra-class variance and decreasing inter-class variance in VHR images make it more difficult to manually design classification features [
8,
9]. Therefore, the traditional methods based on hand-crafted features are no longer suitable for building extraction in VHR images [
10,
11,
12,
13]. Fortunately, the rise of deep learning, especially the convolutional neural network (CNN), has brought us new solutions, as it can automatically learn effective classification features. In recent years, with the development of semantic segmentation technology, building extraction from ORS images has been continuously improved.
In earlier studies, semantic labels have been independently determined pixel by pixel using patch-based CNN models, which predict the label relying on only a small patch around the target pixel and ignores the inherent relationship between patches. Patch-based CNN models have achieved remarkable performance in building extraction, while they cannot guarantee the spatial continuity and integrity of the building structures [
14,
15]. Moreover, patch-based CNN methods are time consuming.
To overcome the problems of patch-based CNNs, Long et al. [
16] proposed the fully convolutional networks (FCNs), which have become a new paradigm for semantic segmentation. FCNs replace the fully connected layers in traditional CNNs with convolutional layers and upsampling layers. Based on the basic FCN8 model [
16], several modifications of FCNs have been proposed. For example, DeconvNet [
17], SegNet [
18] and U-net [
19] used the encoder-decoder structure to improve the segmentation accuracy, FastFCN [
20] proposed Joint Pyramid Upsampling (JPU) to extract high-resolution feature maps and DeepLab [
21] used the dilated convolution to enlarge model receptive field.
To train supervised neural network models, datasets with large number of tagged samples are necessary. In recent years, as more and more remote sensing datasets have become available, FCNs have drawn increasing attention in building extraction research and demonstrated remarkable classification ability on different datasets such as the WHU dataset [
22,
23], the Massachusetts dataset [
6,
24], and the Inria Aerial Image Labeling dataset [
7,
25,
26].
Compared with the natural image semantic segmentation tasks, there are two challenges for building extraction from high-resolution ORS images. One is how to accurately extract the regularized contours of buildings. The other one is that buildings in different areas show complex shapes and diverse scales. The scales of different buildings may vary by dozens of times.
Regardless of the diversity of building shapes, they have clear contours. The most commonly used loss function in building extraction is cross-entropy loss function, but it only focuses on the accuracy of single pixel classification. Therefore, the spatial continuity of building shapes is entirely dependent on the features extracted by the models. In order to get accurate contours, some researchers choose to use post-processing methods. A common post-processing method to capture fine edge details is conditional random fields (CRFs) [
27]. Shrestha et al. [
28] proposed a ELU-FCN model, which replaced the rectified linear unit (ReLU) in FCN8 with the exponential linear unit (ELU) [
29], to extract preliminary building maps and then used CRFs to recover accurate building boundaries. Alshehhi et al. [
30] extracted features with a single patch-based CNN architecture and integrated them with low-level features of adjacent regions during the post-processing stage to improve the performance. Another branch to solve the contour problem is to use the generative adversarial networks (GANs) [
31]. GANs have achieved great success in image conversion [
32,
33] and super-resolution reconstruction [
34,
35]. A GAN model consists of two parts: a generator network and a discriminator network. These two networks are trained with adversarial strategy alternatively until the discriminator cannot distinguish the generated image from the real one. Many researchers believe that the GANs can enforce spatial label continuity to refine the building boundaries [
8,
25]. Li et al. [
25] adopted a stable learning strategy to train a GAN model and tested it on the Inria dataset and the Massachusetts dataset. Although this model gave the state-of-the-art results on the Inria dataset, it needed 21 days to train even on a NVIDIA K80 GPU. In addition, the GAN model is prone to collapse, leading to an extremely unstable training procedure. In contrast to the above methods only using RGB images, some studies improved the extraction accuracy of building boundaries by introducing additional geographic information (digital elevation model (DEM), digital surface model (DSM), etc.) [
36,
37].
Besides the contour problem in building extraction, the buiding sizes can vary greatly, even in one remote sensing image. To deal with the multi-scale problem, one way is to keep the network model unchanged and train the model with input images of different scales. Ji et al. [
5] used the original images and double down-sampled images to train one Siamese U-Net (SiU-Net) model simultaneously and share weights between two networks. Although the model can simultaneously learn multi-scale features of the buildings, the training resources are double, which greatly reduces the training efficiency. In order to improve efficiency, researchers reuse single-scale inputs and hope that deep networks can simultaneously exploit multi-scale features extracted by different layers. There are two branches here. The first is to study multi-scale feature extraction block and output one building extraction map [
22,
24,
38]. The JointNet [
24] gave a new dense atrous convolution block (DACB), which used dense connectivity block and atrous convolution to acquire multi-scale features. Through extensive use of the DACB modules, the JointNet has achieved the best results on the Massachusetts dataset, while consuming a large amount of GPU memory. Another branch uses the multiple outputs of the middle layer to constrain the model [
39,
40,
41,
42]. Ji et al. [
40] proposed a scale-robust FCN (SR-FCN) and trained it with five outputs of two atrous spatial pyramid pooling (ASPP) structures.
On the one hand, high-resolution focal detail features are indispensable to improve the accuracy of building contour extraction. On the other hand, in order to extract buildings with varying morphologies and scales, global semantic features are the key. Furthermore, to use more context information, models tend to enlarge receptive fields [
24,
40], which will further increase the difficulty of extracting accurate contours. To solve this conflict, Liu et al. [
22] proposed an SRI-Net model to handle the balance between discrimination and detail-preservation abilities. To this end, the SRI-Net used large kernel convolution and the spatial residual inception (SRI) module to preserve detail information while obtaining a large receptive field. These strategies made SRI-Net achieve the best results on the WHU dataset, but also made it computationally expensive.
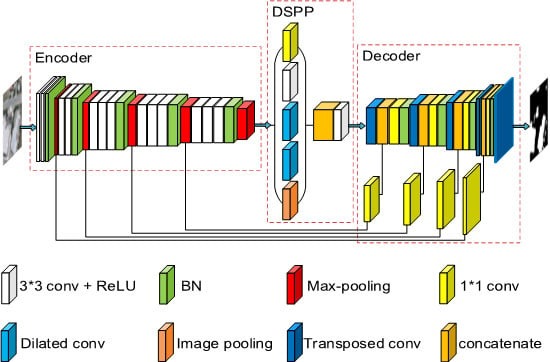
Although FCNs-based models have achieved great success in remote sensing building extraction task, the accuracies of existing results are still not satisfactory due to the poor prediction of boundaries. Moreover, the state-of-the-art models are complex and inefficient, i.e., they are difficult to train and time-consuming to forecast. Furthermore, they are not versatile and can only achieve good results on a single dataset. To solve the foregoing problems, we proposed a simple but efficient U-Net for building extraction, named EU-Net. The main contributions of this paper can be summarized as follows.
A simple but efficient model EU-Net is proposed for optical remote sensing image building extraction. It can be trained efficiently with large learning rate and large batch size.
By applying the dense spatial pyramid pooling (DSPP) structure, multi-scale dense features can be extracted simultaneously from more compact receptive field and then buildings of different scales can be better detected. By using the focal loss in reverse, we reduced the impact of error labels in the datasets on model training, leading to a significant improvement of the accuracy.
Exhaustive experiments were performed for evaluation and comparison using three public remote sensing building datasets. Compared with the state-of-the-art models on each dataset, the results have demonstrated the universality of the proposed model for building extraction task.
This paper is organized as follows. Some preliminary concepts of neural network are introduced in
Section 2.
Section 3 details the proposed EU-Net and the loss function used in this paper. Then, the datasets, implementation settings and experiment results are illustrated in
Section 4. A series of comparative experiments are discussed in
Section 5. Finally, a conclusion is made in
Section 6.
4. Experimental Results
In this section, we first present detailed dataset description, implementation settings, evaluation metrics and comparative methods. Then, extensive experiments were performed to evaluate the performance of the proposed EU-Net.
4.1. Dataset Description
In this paper, we evaluate the proposed EU-Net on three publicly available building datasets for semantic labeling. The metrics of subsequent experiments are evaluated on the test sets of three datasets.
WHU Building Dataset: This dataset is proposed in [
5] and includes both aerial and satellite images. In this paper, we only use the aerial imagery dataset (0.3 m ground resolution) which has higher label accuracy. Therefore, we use this dataset to evaluate the accuracy of building extraction. The aerial dataset contains 8189 tiles with 512*512 pixels. Paper [
5] divided the samples into three parts: a training set (4736 tiles with 130,500 buildings), a validation set (1036 tiles with 14,500 buildings) and a test set (2416 tiles with 42,000 buildings). An example is shown in
Figure 3.
Massachusetts Building Dataset: This dataset is proposed in [
6]. Unlike the WHU dataset, the ground resolution of this dataset is 1m, which is relatively low. The label accuracy of this dataset is also lower than the WHU dataset. Thus, we use this dataset to evaluate the ability to handle fuzzy images. There are 151 images with 1500*1500 pixels and paper [
6] divided them into three parts: a training set of 137 images, a validation set of 4 images and a test set of 10 images. An example is shown in
Figure 4.
Inria Aerial Image Labeling Dataset: This dataset is proposed in [
7] and includes 180 images with public labels and 180 images without public labels. For quantitative analysis, we only use the former in this paper. There are five dissimilar urban settlements (Austin, Chicago, Kitsap County, Western Tyrol and Vienna) with 36 images respectively, ranging from densely populated areas to alpine towns. Since the label accuracy of this dataset is lower than the first dataset, we use this dataset to evaluate the generalization ability of the model. The ground resolution of this dataset is also 0.3 m and image size is 5000*5000 pixels. The first five images of each city are set as test images. An example is shown in
Figure 5.
4.2. Implementation Settings
Due to hardware limitations, raw images are too large to be directly used for training. In this paper, the raw images are cropped into 512*512 patches in preprocessing with no overlap. The WHU dataset has 4736 512*512 patches, the Massachusetts dataset has 1065 512*512 patches, and the Inria dataset has 15,500 512*512 patches. Then, in each iteration, a batch is clipped to 256*256 pixels using the same random cropping to further increase the diversity of the training samples. Except for random cropping, we do not use other data augmentation tricks such as rotation and flip.
We implemented our EU-Net model based on the Keras API in TensorFlow framework. In the experiments, we did not use any pre-training parameters. The convolution kernels were initialized with Glorot uniform initializer [
55] and the biases were initialized to 0. Our proposed network was trained from scratch using SGD optimizer with batch size 64, momentum 0.9. Unlike most literature, we did not use any learning rate adjustment strategies. For the WHU dataset and the Inria dataset, the learning rate was set to 0.2. And for the Massachusetts dataset, the learning rate was set to 0.5. As for the
in (
6), we set 0 for the WHU dataset, and 2 for the Massachusetts dataset and the Inira dataset. This was because the WHU dataset had a high-precision label and therefore did not require the FL. The model was trained using two NVIDIA GeForce GTX 1080Ti and tested with one. We trained EU-Net 300 epochs with WHU dataset, 2000 epochs with Massachusetts dataset, and 400 epochs with Inria dataset.
4.3. Evaluation Metrics
To assess the quantitative performance, four benchmark metrics are used, i.e., recall (Rec), precision (Pre), F1 score (F1) and intersection over union (IoU). These four metrics are defined as:
where TP, FP and FN are the number of true positives, false positives and false negatives, respectively. In addition, we will give the normalized confusion matrix, following [
56,
57]. The form of normalized confusion matrix is shown in
Figure 6. The indexes in the
row denote the rates of the pixels that are classified as each class from the
class.
As we all know, every building has a clear boundary, no matter how the shape of the building changes. Therefore, in addition to using the original mask labels, we also create contour labels to evaluate the model. The criterion for judging whether a building pixel belongs to the contour is based on whether there are background pixels among its four adjacent pixels. If the judgment is true, then the pixel is a contour pixel, and vice versa. An example of the contour label in WHU dataset is shown in
Figure 7.
The four metrics based on mask labels and contour labels are both presented in the subsequent experiments.
In addition to extraction accuracy, the efficiency of the model is also our focus. Considering that the size of the original image in the WHU dataset is only 512*512 pixels, we use the number of images processed per second by the model as a metric. As for the other two datasets, we use the time processing an image as the metric.
4.4. Comparing Methods
To demonstrate its superior performance, the proposed EU-Net is compared with the state-of-the-art methods on each dataset. In this subsection, we will give a brief introduction of the best performing model on each dataset. In addition, we use the results of DeepLabv3+ and FastFCN as the benchmarks for all three datasets.
SRI-Net: Liu et al. [
22] proposed SRI-Net for building detection, which was tested on the WHU dataset and the Inria dataset. According to our research, it achieved the best performance on the WHU dataset. We reproduced the SRI-Net with the Keras API and retrained it on the WHU dataset. We followed the training settings in [
22]: an Adam optimizer was initialized with a learning rate of 1 × 10
, the learning rate was decayed at a rate of 0.9 per epoch, L2 regularization was introduced with a weight decay of 0.0001. Cross-entropy was used as loss function. We trained SRI-Net 300 epochs on WHU dataset.
JointNet: Zhang et al. [
24] proposed JointNet for building detection, which was tested on the Massachusetts dataset. According to our research, it achieved the best performance on this dataset. We reproduced the JointNet with the Keras API and retrained it on the Massachusetts dataset. We followed the training settings in [
24]: an Adam optimizer was initialized with a learning rate of 1 × 10
, and focal loss was used as loss function. We trained JointNet 400 epochs on Massachusetts dataset.
Web-Net: Zhang et al. [
38] proposed a nested encoder-decoder deep network for building extraction, named Web-Net. To balance the local cues and the structural consistency, the Web-Net used the Ultra-Hierarchical Sampling (UHS) blocks to extract and fuse the inter-level features. According to our research, it achieved the best performance on the Inria dataset. In order to achieve the best result, Web-Net had to use the pretrained parameters from ImageNet.
FastFCN: The FastFCN model was proposed by Wu et al. [
20] and achieved the state-of-the-art results on the ADE20K dataset and the PASCAL Context dataset. We reproduced the FastFCN with the Keras API. We trained FastFCN 300 epochs on WHU dataset, 1600 epochs on Massachusetts dataset, and 350 epochs on Inria dataset. FastFCN was trained with SGD, of which the momentum was set to 0.9 and the weight decay was set to 1 × 10
. We set the learning rate to 0.1 and reduced it following the ‘poly’ strategy. Loss function was kept same with EU-Net.
DeepLabv3+: The DeepLab networks were proposed by Chen et al. and have been improved several times, including v1 [
21], v2 [
58], v3 [
59], and v3+ [
49]. The DeepLabv3+ achieved the state-of-the-art results on the Cityscapes dataset and the PASCAL VOC 2012 dataset. We reproduced the DeepLabv3+ with the Keras API. We trained DeepLabv3+ 300 epochs on WHU dataset, 1600 epochs on Massachusetts dataset, and 400 epochs on Inria dataset. DeepLabv3+ was trained with SGD, of which the momentum was set to 0.9 and the weight decay was set to 1 × 10
. We set the learning rate to 0.01 for WHU dataset, 0.5 for Massachusetts dataset, and 0.01 for Inria dataset. We also reduced the learning rate following the ’poly’ strategy. Loss function was kept same with EU-Net.
4.5. Comparison with Deep Models
4.5.1. WHU Dataset
Table 2 gives the quantitative evaluation indexes of different models on the test images of the WHU dataset. Our proposed EU-Net outperforms SRI-Net, FastFCN, and DeepLabv3 on all the four metrics, except for the precision of SRI-Net. However, the precision of our EU-Net is only 0.23% lower than that of SRI-Net, and our EU-Net makes a better balance between recall and precision, as can be intuitively seen from the F1. The mask IoU metrics are all higher than 85% and our EU-Net even exceeds 90%. This is because the WHU dataset is of higher quality and is easier to distinguish than the other two datasets [
22]. Compared with the result of SRI-Net in [
22], our EU-Net improved the mask IoU by 1.47%. Moreover, our model can process 16.78 images per second, while SRI-Net can only process 8.51 images per second. In other words, our model efficiency is approximately twice that of the latter. The FastFCN and the DeepLabv3+ are also much slower than our model. As a reference, we also presented the normalized confusion matrix for EU-Net in
Figure 8.
Figure 9 shows the visual performance of four different scenarios. The first scenario is an example of an oversized building. The result of FastFCN was very terrible where the oversized building was almost undetected. SRI-Net and DeepLabv3+ misclassified the cement floor in the lower middle area into buildings, while our EU-Net successfully avoided this error. The second scenario is sparsely distributed medium-sized buildings. Only our EU-Net successfully detected the building in the upper left corner and all four models misclassified the containers in the lower right corner into buildings. The third scenario is densely distributed small-sized buildings. All four models missed several buildings of very small size. The fourth scenario is a negative sample. Only our EU-Net gave the right prediction and the other three models had more or less misclassifications. In summary, our EU-Net gives the best results both on the integrity of building shapes and the accuracy of building contours.
4.5.2. Massachusetts Dataset
In this dataset, we predicted the test images in blocks of 512*512 pixels, with a sliding stride of 256 pixels.
Table 3 gives the quantitative evaluation indexes and time costs of processing one image for different models. It is clear that our proposed EU-Net outperforms JointNet, FastFCN, and DeepLabv3+. Compared with the results of the WHU dataset, all metrics are much lower for the four models. There are two reasons for the results. First, the scenes of the Massachusetts dataset are more complicated. Especially the shadows of high buildings bring great difficulties to the classification. Second, the Massachusetts dataset has a lower resolution and label quality. As shown in
Table 3, recall metrics for all models are much lower than the precision metrics and our model has the smallest gap between the two metrics. Compared with the report result of JointNet in [
24], our EU-Net improved the IoU by 1.94%. In terms of processing efficiency, the FastFCN is almost the same as the DeepLabv3+, and the time to process one image is nearly twice that of our model. The most time-consuming JointNet takes more than three times as much as our model. As a reference, we also presented the normalized confusion matrix for EU-Net in
Figure 10.
Figure 11 shows the visual performance of four different scenarios. The odd rows are original images and the even rows are the regions of interest selected by red boxes in the original images. The first scenario showed the impact of high-rise shadows on the accuracy of building extraction. It could be seen that the buildings predicted by four models were all incomplete and the integrity of DeepLabv3+ was the worst. Although the integrity of FastFCN was better than DeepLabv3+, there was a significant sawtooth effect on the building contours. Our EU-Net gave the most complete and accurate building extraction results. The main problem was that the shadows in the middle of the buildings cannot be accurately classified. As mentioned before, there exist obvious wrong labels in Massachusetts dataset. An example of error labels is shown in the 4th and 8th row of
Figure 11, where the ground truth presents a wrong label on the grassland area. The last two scenarios were used to show the performance of four models for detecting buildings of different sizes. For small and medium-sized buildings, JointNet, DeepLabv3+ and EU-Net had similar performance. Meanwhile, for oversized buildings, only our EU-Net gave a relatively complete prediction.
4.5.3. Inria Dataset
The test image size is the same as the Massachusetts dataset.
Table 4 gives the quantitative evaluation indexes and time costs of processing one image for different models. Similar conclusions can be drawn from
Table 4. The results on the Inria dataset are also worse than the WHU dataset, but better than the Massachusetts dataset. The latter is because the resolution of the Inria dataset is higher than the resolution of the Massachusetts dataset. Compared with the WHU dataset, the Inria dataset has a lower quality where some obvious error labels can be found in the ground truth. Moreover, the scenes of the Inria dataset are more complicated, as there are five different cities in the dataset. These factors cause the results on the Inria dataset to be worse than the WHU dataset. Compared with the result of Web-Net reported in [
38], our EU-Net improved the mask IoU by 0.4%. According to paper [
38], the Web-Net takes 56.5 s to process one image, while the EU-Net only needs 14.79 s, i.e., our model has improved the efficiency four times compared with the Web-Net. As a reference, we also presented the normalized confusion matrix for EU-Net in
Figure 12.
We also test the performance of EU-Net on five cities respectively, showed in
Table 5. Compared with Web-Net, the proposed EU-Net gained better performance on Austin, Chicago, and Vienna. But for Kitsap and Tyrol-w, Web-Net performed better. In general, the overall performance of the proposed EU-Net is slightly better than Web-Net.
We selected a representative image from each of the five cities, as shown in
Figure 13. The buildings in Kitsap County (the third row in
Figure 13) are randomly scattered throughout the image and the buildings in Western Tyrol (the fourth row in
Figure 13) are concentrated in parts of the image. The buildings of the other three cities are densely distributed throughout the images. Among them, the buildings in Chicago (the second row in
Figure 13) are neatly distributed, while the buildings in Austin (the first row in
Figure 13) and Vienna (the last row in
Figure 13) are irregular. Compared with Austin, the building size varies drastically in Vienna.
Roughly speaking, the three model predictions are visually similar. In order to compare the details, we enlarged the red boxes in
Figure 13, shown in
Figure 14. From top to bottom are Austin, Chicago, Kitsap, Tyrol and Vienna. For the large buildings in Austin, the predictions of FastFCN and our model were more complete than DeepLabv3+, and the contour accuracy of DeepLabv3+ and our model was better than that of FastFCN. Moreover, there were some misclassifications of small-size buildings in the predictions of FastFCN and DeepLabv3+. For the Chicago, there are many neatly arranged buildings. In the prediction of FastFCN, the adjacent buildings were treated as a whole. The prediction of DeepLabv3+ was slightly better, and only EU-Net successfully distinguished these buildings. In addition, the selected areas in Chicago showed some error labels. Although all three models gave correct predictions for these areas, they gave some false alarms as shown in the yellow rectangles. Moreover, the large building in the prediction of DeepLabv3+ obviously missed the right piece. As for the Kitsap, all buildings in the selected area were error labels. Our EU-Net showed a bad performance while the predictions of DeepLabv3+ and FastFCN only had a few noises in the selected area. We ascribed the bad performance to the simple encoder of EU-Net. Compared with the other four cities, there were much fewer buildings in Kitsap, and thus it was difficult for models to learn enough effective features to correctly extract the buildings in Kitsap, especially for our simple encoder. This conclusion can be also drawn from the quantitative indexes on Kitsap among the five cities. Because there were few buildings in the Kitsap, the error labels had a great influence on the evaluation metrics, leading to abnormally low metrics in this area. If we ignored these obviously error labels, the IoU metrics for EU-Net, DeepLabv3+ and FastFCN could be improved by 4.91%, 7.83% and 7.50%, which were obvious improvements. There are four large buildings in Tyrol. The prediction results of FastFCN and DeepLabv3+ missed two of them while the EU-Net extracted four buildings. As for the enlarged areas in Vienna, the buildings in yellow box were under construction. It is clear that the FastFCN and DeepLabv3+ both failed to extract the two buildings, and the proposed EU-Net successfully detected one of them.