Spatial Modeling of Snow Avalanche Using Machine Learning Models and Geo-Environmental Factors: Comparison of Effectiveness in Two Mountain Regions
Abstract
:1. Introduction
2. Materials and Methods
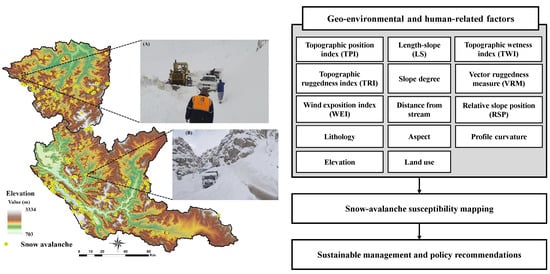
2.1. Study Area
2.2. Dataset Used
2.2.1. Snow Avalanche Inventory
2.2.2. Factors Influencing Snow Avalanches
2.3. Methodology
2.3.1. Generating Snow Avalanche Hazard Maps
2.3.2. Accuracy Assessments
2.3.3. Ensemble Modeling
2.3.4. Statistical Comparison of Models
Friedman Test
Wilcoxon Signed-rank Test
3. Results
3.1. Snow Avalanche Hazard Maps
3.2. Performance of Models
3.3. Statistical Comparison of Models
3.3.1. Friedman Test
3.3.2. Wilcoxon Signed-Rank Test
3.4. Variable Importance
4. Discussion
4.1. The Performance of Models
4.2. Statistical Comparison of Models
4.3. Variable Importance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blahut, J.; Klimeš, J.; Balek, J.; Hájek, P.; Červená, L.; Lysák, J. Snow avalanche hazard of the Krkonoše National Park, Czech Republic. J. Maps 2017, 13, 86–90. [Google Scholar] [CrossRef] [Green Version]
- Abdollahi, S.; Pourghasemi, H.R.; Ghanbarian, G.A.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2018, 78, 4017–4034. [Google Scholar] [CrossRef]
- Arpaci, A.; Malowerschnig, B.; Sass, O.; Vacik, H. Using multi variate data mining techniques for estimating fire susceptibility of Tyrolean forests. Appl. Geogr. 2014, 53, 258–270. [Google Scholar] [CrossRef]
- Barbolini, M.; Natale, L.; Savi, F. Effects of release conditions uncertainty on avalanche hazard mapping. Nat. Hazards 2002, 25, 225–244. [Google Scholar] [CrossRef]
- Barbolini, M.; Pagliardi, M.; Ferro, F.; Corradeghini, P. Avalanche hazard mapping over large undocumented areas. Nat. Hazards 2011, 56, 451–464. [Google Scholar] [CrossRef]
- Bebi, P.; Kulakowski, D.; Rixen, C. Snow avalanche disturbances in forest ecosystems—State of research and implications for management. For. Ecol. Manag. 2009, 257, 1883–1892. [Google Scholar] [CrossRef]
- Bergua, S.B.; Piedrabuena, M.Á.P.; Alfonso, J.L.M. Snow avalanches, land use changes, and atmospheric warming in landscape dynamics of the Atlantic mid-mountains (Cantabrian Range, NW Spain). Appl. Geogr. 2019, 107, 38–50. [Google Scholar] [CrossRef]
- Bernhardt, M.; Zängl, G.; Liston, G.; Strasser, U.; Mauser, W. Using wind fields from a high-resolution atmospheric model for simulating snow dynamics in mountainous terrain. Hydrol. Process. Int. J. 2009, 23, 1064–1075. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Bhargavi, P.; Jyothi, S. Applying naive bayes data mining technique for classification of agricultural land soils. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 117–122. [Google Scholar]
- Böhner, J.; Antonić, O. Land-surface parameters specific to topo-climatology. Dev. Soil Sci. 2009, 33, 195–226. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Bühler, Y.; Kumar, S.; Veitinger, J.; Christen, M.; Stoffel, A.; Snehmani, S. Automated identification of potential snow avalanche release areas based on digital elevation models. Nat. Hazards Earth Syst. Sci. 2013, 13, 1321–1335. [Google Scholar] [CrossRef]
- Bühler, Y.; Rickenbach, D.; Stoffel, A.; Margreth, S.; Stoffel, L.; Christen, M. Automated snow avalanche release area delineation–validation of existing algorithms and proposition of a new object-based approach for large-scale hazard indication mapping. Nat. Hazards Earth Syst. Sci. 2018, 18, 3235–3251. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Ngo, P.-T.T.; Pham, T.D.; Jaafari, A.; Minh, N.Q.; Hoa, P.V.; Samui, P. A novel hybrid approach based on a swarm intelligence optimized extreme learning machine for flash flood susceptibility mapping. Catena 2019, 179, 184–196. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Bunn, A.G.; Hughes, M.K.; Salzer, M.W. Topographically modified tree-ring chronologies as a potential means to improve paleoclimate inference. Clim. Chang. 2011, 105, 627–634. [Google Scholar] [CrossRef]
- Cama, M.; Lombardo, L.; Conoscenti, C.; Rotigliano, E. Improving transferability strategies for debris flow susceptibility assessment: Application to the Saponara and Itala catchments (Messina, Italy). Geomorphology 2017, 288, 52–65. [Google Scholar] [CrossRef]
- Casteller, A.; Häfelfinger, T.; Cortés Donoso, E.; Podvin, K.; Kulakowski, D.; Bebi, P. Assessing the interaction between mountain forests and snow avalanches at Nevados de Chillán, Chile and its implications for ecosystem-based disaster risk reduction. Nat. Hazards Earth Syst. Sci. 2018, 18, 1173–1186. [Google Scholar] [CrossRef] [Green Version]
- Che, V.B.; Kervyn, M.; Suh, C.E.; Fontijn, K.; Ernst, G.G.; Del Marmol, M.-A.; Trefois, P.; Jacobs, P. Landslide susceptibility assessment in Limbe (SW Cameroon): A field calibrated seed cell and information value method. Catena 2012, 92, 83–98. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive Bayes and RBFNetwork models for the Long County area (China). Bull. Eng. Geol. Environ. 2019, 78, 247–266. [Google Scholar] [CrossRef]
- Choubin, B.; Borji, M.; Mosavi, A.; Sajedi-Hosseini, F.; Singh, V.P.; Shamshirband, S. Snow avalanche hazard prediction using machine learning methods. J. Hydrol. 2019, 577, 123929. [Google Scholar] [CrossRef]
- Confortola, G.; Maggioni, M.; Freppaz, M.; Bocchiola, D. Modelling soil removal from snow avalanches: A case study in the North-Western Italian Alps. Cold Reg. Sci. Technol. 2012, 70, 43–52. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1. 4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef] [Green Version]
- Covăsnianu, A. Mapping Snow Avalanche Risk Using GIS Technique and 3D Modeling: Case Study Ceahlau National Park. Available online: SSRN 1884082 2011 (accessed on 24 June 2019).
- Dadic, R.; Mott, R.; Lehning, M.; Burlando, P. Wind influence on snow depth distribution and accumulation over glaciers. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Darabi, H.; Choubin, B.; Rahmati, O.; Haghighi, A.T.; Pradhan, B.; Kløve, B. Urban flood risk mapping using the GARP and QUEST models: A comparative study of machine learning techniques. J. Hydrol. 2019, 569, 142–154. [Google Scholar] [CrossRef]
- de Bouchard d’Aubeterre, G.; Favillier, A.; Mainieri, R.; Saez, J.L.; Eckert, N.; Saulnier, M.; Peiry, J.-L.; Stoffel, M.; Corona, C. Tree-ring reconstruction of snow avalanche activity: Does avalanche path selection matter? Sci. Total Environ. 2019, 684, 496–508. [Google Scholar] [CrossRef]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Eckerstorfer, M.; Bühler, Y.; Frauenfelder, R.; Malnes, E. Remote sensing of snow avalanches: Recent advances, potential, and limitations. Cold Reg. Sci. Technol. 2016, 121, 126–140. [Google Scholar] [CrossRef]
- Eckerstorfer, M.; Malnes, E. Manual detection of snow avalanche debris using high-resolution Radarsat-2 SAR images. Cold Reg. Sci. Technol. 2015, 120, 205–218. [Google Scholar] [CrossRef]
- Eckert, N.; Keylock, C.; Bertrand, D.; Parent, E.; Faug, T.; Favier, P.; Naaim, M. Quantitative risk and optimal design approaches in the snow avalanche field: Review and extensions. Cold Reg. Sci. Technol. 2012, 79, 1–19. [Google Scholar] [CrossRef]
- Falah, F.; Rahmati, O.; Rostami, M.; Ahmadisharaf, E.; Daliakopoulos, I.N.; Pourghasemi, H.R. Artificial Neural Networks for Flood Susceptibility Mapping in Data-Scarce Urban Areas. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 323–336. [Google Scholar]
- Farid, D.M.; Zhang, L.; Rahman, C.M.; Hossain, M.A.; Strachan, R. Hybrid decision tree and naïve Bayes classifiers for multi-class classification tasks. Expert Syst. Appl. 2014, 41, 1937–1946. [Google Scholar] [CrossRef]
- Formetta, G.; Capparelli, G.; Versace, P. Evaluating performance of simplified physically based models for shallow landslide susceptibility. Hydrol. Earth Syst. Sci. 2016, 20, 4585–4603. [Google Scholar] [CrossRef] [Green Version]
- Fornaciai, A.; Bisson, M.; Landi, P.; Mazzarini, F.; Pareschi, M.T. A LiDAR survey of Stromboli volcano (Italy): Digital elevation model-based geomorphology and intensity analysis. Int. J. Remote Sens. 2010, 31, 3177–3194. [Google Scholar] [CrossRef]
- Gądek, B.; Kaczka, R.J.; Rączkowska, Z.; Rojan, E.; Casteller, A.; Bebi, P. Snow avalanche activity in Żleb Żandarmerii in a time of climate change (Tatra Mts., Poland). Catena 2017, 158, 201–212. [Google Scholar]
- Ganteaume, A.; Jappiot, M. What causes large fires in Southern France. For. Ecol. Manag. 2013, 294, 76–85. [Google Scholar] [CrossRef]
- Garosi, Y.; Sheklabadi, M.; Conoscenti, C.; Pourghasemi, H.R.; Van Oost, K. Assessing the performance of GIS-based machine learning models with different accuracy measures for determining susceptibility to gully erosion. Sci. Total Environ. 2019, 664, 1117–1132. [Google Scholar] [CrossRef]
- Gayen, A.; Pourghasemi, H.R.; Saha, S.; Keesstra, S.; Bai, S. Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total Environ. 2019, 668, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Germain, D. Snow avalanche hazard assessment and risk management in northern Quebec, eastern Canada. Nat. Hazards 2016, 80, 1303–1321. [Google Scholar] [CrossRef]
- Ghinoi, A.; Chung, C.-J. STARTER: A statistical GIS-based model for the prediction of snow avalanche susceptibility using terrain features—Application to Alta Val Badia, Italian Dolomites. Geomorphology 2005, 66, 305–325. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Aryal, J.; Gholaminia, K. A new GIS-based technique using an adaptive neuro-fuzzy inference system for land subsidence susceptibility mapping. J. Spat. Sci. 2018, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of different machine learning methods and deep-learning convolutional neural networks for landslide detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. Multi-criteria risk evaluation by integrating an analytical network process approach into GIS-based sensitivity and uncertainty analyses. Geomat. Nat. Hazards Risk 2018, 9, 127–151. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Srivastava, P.K.; Snehmani. GIS-based MCDA–AHP modelling for avalanche susceptibility mapping of Nubra valley region, Indian Himalaya. Geocarto Int. 2017, 32, 1254–1267. [Google Scholar] [CrossRef]
- Goetz, J.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Grabs, T.; Seibert, J.; Bishop, K.; Laudon, H. Modeling spatial patterns of saturated areas: A comparison of the topographic wetness index and a dynamic distributed model. J. Hydrol. 2009, 373, 15–23. [Google Scholar] [CrossRef] [Green Version]
- Gruber, U.; Bartelt, P. Snow avalanche hazard modelling of large areas using shallow water numerical methods and GIS. Environ. Model. Softw. 2007, 22, 1472–1481. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models, 1st ed.; Chapman and Hall: London, UK, 1990; p. 352. [Google Scholar]
- Hinckley, E.L.S.; Ebel, B.A.; Barnes, R.T.; Anderson, R.S.; Williams, M.W.; Anderson, S.P. Aspect control of water movement on hillslopes near the rain–snow transition of the Colorado Front Range. Hydrol. Process. 2014, 28, 74–85. [Google Scholar] [CrossRef]
- Ho, T.K.; Hull, J.J.; Srihari, S.N. Decision combination in multiple classifier systems. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 66–75. [Google Scholar]
- Jamieson, B.; Margreth, S.; Jones, A. Application and limitations of dynamic models for snow avalanche hazard mapping. In Proceedings of the Whistler 2008 International Snow Science Workshop, Whistler, BC, Canada, 21–27 September 2008; p. 730. [Google Scholar]
- Janik, P.; Lobos, T. Automated classification of power-quality disturbances using SVM and RBF networks. IEEE Trans. Power Deliv. 2006, 21, 1663–1669. [Google Scholar] [CrossRef] [Green Version]
- Johnson, A.L.; Smith, D.J. Geomorphology of snow avalanche impact landforms in the southern Canadian Cordillera. Can. Geogr. Géographe Can. 2010, 54, 87–103. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Kern, A.N.; Addison, P.; Oommen, T.; Salazar, S.E.; Coffman, R.A. Machine learning based predictive modeling of debris flow probability following wildfire in the intermountain Western United States. Math. Geosci. 2017, 49, 717–735. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Kritikos, T.; Robinson, T.R.; Davies, T.R. Regional coseismic landslide hazard assessment without historical landslide inventories: A new approach. J. Geophys. Res. Earth Surf. 2015, 120, 711–729. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Snehmani;Srivastava, P.K.; Gore, A.; Singh, M.K. Fuzzy–frequency ratio model for avalanche susceptibility mapping. Int. J. Digit. Earth 2016, 9, 1168–1184. [Google Scholar] [CrossRef]
- Kumar, S.; Srivastava, P.K. Geospatial Modelling and Mapping of Snow Avalanche Susceptibility. J. Indian Soc. Remote Sens. 2018, 46, 109–119. [Google Scholar] [CrossRef]
- Kumar, S.; Srivastava, P.K.; Bhatiya, S. Geospatial probabilistic modelling for release area mapping of snow avalanches. Cold Reg. Sci. Technol. 2019, 165, 102813. [Google Scholar] [CrossRef]
- Leroy, B.; Delsol, R.; Hugueny, B.; Meynard, C.N.; Barhoumi, C.; Barbet-Massin, M.; Bellard, C. Without quality presence–absence data, discrimination metrics such as TSS can be misleading measures of model performance. J. Biogeogr. 2018, 45, 1994–2002. [Google Scholar] [CrossRef]
- Linden, A. Measuring diagnostic and predictive accuracy in disease management: An introduction to receiver operating characteristic (ROC) analysis. J. Eval. Clin. Pract. 2006, 12, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Bu, R.; Liu, J.; Leng, W.; Hu, Y.; Yang, L.; Liu, H. Predicting the wetland distributions under climate warming in the Great Xing’an Mountains, northeastern China. Ecol. Res. 2011, 26, 605–613. [Google Scholar] [CrossRef]
- Lombardo, L.; Bachofer, F.; Cama, M.; Märker, M.; Rotigliano, E. Exploiting Maximum Entropy method and ASTER data for assessing debris flow and debris slide susceptibility for the Giampilieri catchment (north-eastern Sicily, Italy). Earth Surf. Process. Landf. 2016, 41, 1776–1789. [Google Scholar] [CrossRef] [Green Version]
- Matthews, J.A.; McEwen, L.J.; Owen, G. Schmidt-hammer exposure-age dating (SHD) of snow-avalanche impact ramparts in southern Norway: Approaches, results and implications for landform age, dynamics and development. Earth Surf. Process. Landf. 2015, 40, 1705–1718. [Google Scholar] [CrossRef]
- Matthews, J.A.; Owen, G.; McEwen, L.J.; Shakesby, R.A.; Hill, J.L.; Vater, A.E.; Ratcliffe, A.C. Snow avalanche impact craters in southern Norway: Their morphology and dynamics compared with small terrestrial meteorite craters. Geomorphology 2017, 296, 11–30. [Google Scholar] [CrossRef]
- McGarigal, K.; Tagil, S.; Cushman, S.A. Surface metrics: An alternative to patch metrics for the quantification of landscape structure. Landsc. Ecol. 2009, 24, 433–450. [Google Scholar] [CrossRef]
- Meena, S.R.; Ghorbanzadeh, O.; Blaschke, T. A comparative study of statistics-based landslide susceptibility models: A case study of the region affected by the Gorkha Earthquake in Nepal. ISPRS Int. J. Geo-Inf. 2019, 8, 94. [Google Scholar] [CrossRef] [Green Version]
- Meena, S.R.; Mishra, B.K.; Tavakkoli Piralilou, S. A Hybrid Spatial Multi-Criteria Evaluation Method for Mapping Landslide Susceptible Areas in Kullu Valley, Himalayas. Geosciences 2019, 9, 156. [Google Scholar] [CrossRef] [Green Version]
- Melville, B.; Lucieer, A.; Aryal, J. Object-based random forest classification of Landsat ETM+ and WorldView-2 satellite imagery for mapping lowland native grassland communities in Tasmania, Australia. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 46–55. [Google Scholar] [CrossRef]
- Moosavi, V.; Niazi, Y. Development of hybrid wavelet packet-statistical models (WP-SM) for landslide susceptibility mapping. Landslides 2016, 13, 97–114. [Google Scholar] [CrossRef]
- Mott, R.; Faure, F.; Lehning, M.; Henning, L.; Hynek, B.; Michlmayer, G.; Prokop, A.; Schӧner, W. Simulation of seasonal snow-cover distribution for glacierized sites on Sonnblick, Austria, with the Alpine3D model. Ann. Glaciol. 2008, 49, 155–160. [Google Scholar] [CrossRef] [Green Version]
- Murphy, M.A.; Evans, J.S.; Storfer, A. Quantifying Bufo boreas connectivity in Yellowstone National Park with landscape genetics. Ecology 2010, 91, 252–261. [Google Scholar] [CrossRef] [Green Version]
- Nefeslioglu, H.A.; Sezer, E.A.; Gokceoglu, C.; Ayas, Z. A modified analytical hierarchy process (M-AHP) approach for decision support systems in natural hazard assessments. Comput. Geosci. 2013, 59, 1–8. [Google Scholar] [CrossRef]
- Park, N.W.; Chi, K.H. Quantitative assessment of landslide susceptibility using high-resolution remote sensing data and a generalized additive model. Int. J. Remote Sens. 2008, 29, 247–264. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Pourghasemi, H.R.; Indra, P.; Dholakia, M. Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Platt, R.V.; Schoennagel, T.; Veblen, T.T.; Sherriff, R.L. Modeling wildfire potential in residential parcels: A case study of the north-central Colorado Front Range. Landsc. Urban Plan. 2011, 102, 117–126. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, X.; Chen, J.-P.; Xiang, L.-J.; Zhang, W.; Niu, C.-C. A novel hybrid KPCA and SVM with PSO model for identifying debris flow hazard degree: A case study in Southwest China. Environ. Earth Sci. 2016, 75, 991. [Google Scholar] [CrossRef]
- Qiu, H.; Cui, P.; Regmi, A.D.; Hu, S.; Wang, X.; Zhang, Y. The effects of slope length and slope gradient on the size distributions of loess slides: Field observations and simulations. Geomorphology 2018, 300, 69–76. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Naghibi, S.A.; Biggs, T.; Soltani, M.; Deo, R.C.; Cerdà, A.; Mohammadi, F.; Bui, D.T. Land subsidence modelling using tree-based machine learning algorithms. Sci. Total Environ. 2019, 672, 239–252. [Google Scholar] [CrossRef]
- Rahmati, O.; Golkarian, A.; Biggs, T.; Keesstra, S.; Mohammadi, F.; Daliakopoulos, I.N. Land subsidence hazard modeling: Machine learning to identify predictors and the role of human activities. J. Environ. Manag. 2019, 236, 466–480. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Deo, R.C.; Conoscenti, C.; Lombardo, L.; Dayal, K.; Taghizadeh-Mehrjardi, R.; Pourghasemi, H.R.; Kumar, S. PMT: New analytical framework for automated evaluation of geo-environmental modelling approaches. Sci. Total Environ. 2019, 664, 296–311. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Characterization and quantification of path dependency in landslide susceptibility. Geomorphology 2017, 292, 16–24. [Google Scholar] [CrossRef]
- Selcuk, L. An avalanche hazard model for Bitlis Province, Turkey, using GIS based multicriteria decision analysis. Turk. J. Earth Sci. 2013, 22, 523–535. [Google Scholar] [CrossRef]
- Sharp, A.E.A. Evaluating the Exposure of Heliskiing Ski Guides to Avalanche Terrain Using a Fuzzy Logic Avalanche Susceptibility Model; University of Leeds: Leeds, UK, 2018. [Google Scholar]
- Singh, D.K.; Mishra, V.D.; Gusain, H.S.; Gupta, N.; Singh, A.K. Geo-spatial Modeling for Automated Demarcation of Snow Avalanche Hazard Areas Using Landsat-8 Satellite Images and In Situ Data. J. Indian Soc. Remote Sens. 2019, 47, 513–526. [Google Scholar] [CrossRef]
- Snehmani;Bhardwaj, A.; Pandit, A.; Ganju, A. Demarcation of potential avalanche sites using remote sensing and ground observations: A case study of Gangotri glacier. Geocarto Int. 2014, 29, 520–535. [Google Scholar] [CrossRef]
- Somodi, I.; Lepesi, N.; Botta-Dukát, Z. Prevalence dependence in model goodness measures with special emphasis on true skill statistics. Ecol. Evol. 2017, 7, 863–872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stanchi, S.; Freppaz, M.; Zanini, E. The influence of Alpine soil properties on shallow movement hazards, investigated through factor analysis. Nat. Hazards Earth Syst. Sci. 2012, 12, 1845–1854. [Google Scholar] [CrossRef] [Green Version]
- Statham, G.; Haegeli, P.; Greene, E.; Birkeland, K.; Israelson, C.; Tremper, B.; Stethem, C.; McMahon, B.; White, B.; Kelly, J. A conceptual model of avalanche hazard. Nat. Hazards 2018, 90, 663–691. [Google Scholar] [CrossRef] [Green Version]
- Tehrany, M.S.; Jones, S.; Shabani, F. Identifying the essential flood conditioning factors for flood prone area mapping using machine learning techniques. Catena 2019, 175, 174–192. [Google Scholar] [CrossRef]
- Minnier, J.; Yuan, M.; Liu, J.S.; Cai, T. Risk classification with an adaptive naive bayes kernel machine model. J. Am. Stat. Assoc. 2015, 110, 393–404. [Google Scholar] [CrossRef] [Green Version]
- Termeh, S.V.R.; Khosravi, K.; Sartaj, M.; Keesstra, S.D.; Tsai, F.T.-C.; Dijksma, R.; Pham, B.T. Optimization of an adaptive neuro-fuzzy inference system for groundwater potential mapping. Hydrogeol. J. 2019, 27, 2511–2534. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide susceptibility assessment in vietnam using support vector machines, decision tree, and Naive Bayes Models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar] [CrossRef] [Green Version]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land subsidence susceptibility mapping in south korea using machine learning algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef] [Green Version]
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar]
- Triola, M.F. Bayes’ Eheorem. PDF. Available online: http://faculty.washington.edu/tamre/BayesTheorem.pdf (accessed on 25 June 2019).
- Valdez, M.C.; Chang, K.-T.; Chen, C.-F.; Chiang, S.-H.; Santos, J.L. Modelling the spatial variability of wildfire susceptibility in Honduras using remote sensing and geographical information systems. Geomat. Nat. Hazards Risk 2017, 8, 876–892. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. Statistical Learning Theory; John Wiley & Sons. Inc.: New York, NY, USA, 1998. [Google Scholar]
- Veitinger, J.; Purves, R.S.; Sovilla, B. Potential slab avalanche release area identification from estimated winter terrain: A multi-scale, fuzzy logic approach. Nat. Hazards Earth Syst. Sci. 2016, 16, 2211. [Google Scholar] [CrossRef] [Green Version]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Vickers, H.; Eckerstorfer, M.; Malnes, E.; Larsen, Y.; Hindberg, H. A method for automated snow avalanche debris detection through use of synthetic aperture radar (SAR) imaging. Earth Space Sci. 2016, 3, 446–462. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.C.; Mohammadi, F.; Biggs, T.; Moghaddam, D.D.; Naghibi, S.A.; Bui, D.T. Machine learning approaches for spatial modeling of agricultural droughts in the south-east region of Queensland Australia. Sci. Total Environ 2020, 669, 134230. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Lin, D.; Sun, L.; Toh, K.-A.; Zhang, J.B.; Lin, Z. Twin SVM with a reject option through ROC curve. J. Frankl. Inst. 2018, 355, 1710–1732. [Google Scholar] [CrossRef]
- Wessel, M.; Brandmeier, M.; Tiede, D. Evaluation of different machine learning algorithms for scalable classification of tree types and tree species based on Sentinel-2 data. Remote Sens. 2018, 10, 1419. [Google Scholar] [CrossRef] [Green Version]
- Wesselink, D.S.; Malnes, E.; Eckerstorfer, M.; Lindenbergh, R.C. Automatic detection of snow avalanche debris in central Svalbard using C-band SAR data. Polar Res. 2017, 36, 1333236. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Lin, H.; Lü, Y.; Luo, Y.; Ren, Y.; Comber, A. A modified change vector approach for quantifying land cover change. Remote Sens. 2018, 10, 1578. [Google Scholar] [CrossRef] [Green Version]
- Yesilnacar, E.K. The Application of Computational Intelligence to Landslide Susceptibility Mapping in Turkey; University of Melbourne: Melbourne, Australia, 2005. [Google Scholar]
- Yi, Y.; Sun, J.; Zhang, S. A habitat suitability model for Chinese sturgeon determined using the generalized additive method. J. Hydrol. 2016, 534, 11–18. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The Staffora River Basin case study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]







| Characteristic | Zarrinehroud Watershed | Darvan Watershed |
|---|---|---|
| Location (province) | In northwest Kurdistan | In southwest Kurdistan and northeast Kermanshah |
| Elevation min (m a.s.l.) | 1372 | 703 |
| Elevation max (m a.s.l.) | 3141 | 3328 |
| Elevation mean (m a.s.l.) | 1886 | 1842 |
| Mean slope (degree) | 14.4 | 15.1 |
| Precipitation (mm/yr) | 487 | 931 |
| Average of wind speed (knots) | 5.1 | 3.5 |
| Annual minimum temperature (°C) | −36 | −27 |
| Annual maximum temperature (°C) | 38.2 | 36.4 |
| Characteristic | Function |
|---|---|
| Linear kernel | |
| Polynomial kernel | |
| Radial based kernel | |
| Sigmoid kernel |
| Watershed | Model | Snow Avalanche Susceptibility | ||||
|---|---|---|---|---|---|---|
| Very Low | Low | Medium | High | Very High | ||
| Darvan Watershed | RF | 51.4 | 13.1 | 10.6 | 12.8 | 12.1 |
| SVM | 45 | 18.9 | 14.6 | 11.7 | 9.8 | |
| NB | 53.7 | 7.1 | 21.7 | 10.3 | 7.2 | |
| GAM | 40.2 | 20.5 | 15.6 | 7.9 | 15.8 | |
| Ensemble | 40.9 | 22.81 | 10.17 | 13.84 | 12.28 | |
| Zarrinehroud Watershed | RF | 49.3 | 15.2 | 11.6 | 11.4 | 12.5 |
| SVM | 43.1 | 19.7 | 15.3 | 10.2 | 11.7 | |
| NB | 54.2 | 8.8 | 19.4 | 9.5 | 8.1 | |
| GAM | 38.9 | 20.4 | 14.1 | 10.4 | 16.2 | |
| Ensemble | 45.2 | 20.62 | 13.18 | 11.65 | 9.35 | |
| Watershed | Model | Goodness-of-Fit | Predictive Performance | ||||
|---|---|---|---|---|---|---|---|
| AUROC | TSS | MCC | AUROC | TSS | MCC | ||
| Darvan Watershed | RF | 0.981 | 0.893 | 0.884 | 0.964 | 0.862 | 0.865 |
| SVM | 0.972 | 0.882 | 0.863 | 0.955 | 0.844 | 0.858 | |
| NB | 0.932 | 0.791 | 0.855 | 0.914 | 0.727 | 0.847 | |
| GAM | 0.924 | 0.756 | 0.812 | 0.896 | 0.714 | 0.796 | |
| Ensemble | 0.977 | 0.886 | 0.871 | 0.966 | 0.865 | 0.861 | |
| Zarrinehroud Watershed | RF | 0.973 | 0.882 | 0.866 | 0.956 | 0.881 | 0.854 |
| SVM | 0.965 | 0.863 | 0.859 | 0.948 | 0.875 | 0.832 | |
| NB | 0.941 | 0.835 | 0.825 | 0.922 | 0.824 | 0.804 | |
| GAM | 0.934 | 0.835 | 0.808 | 0.905 | 0.816 | 0.793 | |
| Ensemble | 0.968 | 0.877 | 0.862 | 0.958 | 0.877 | 0.841 | |
| No. | Darvan Watershed | Zarrinehroud Watershed | ||||
|---|---|---|---|---|---|---|
| Model | X2 | p | Model | X2 | p | |
| 1 | RF | 121.502 | 0.000 | RF | 91.825 | 0.000 |
| 2 | SVM | SVM | ||||
| 3 | NB | NB | ||||
| 4 | GAM | GAM | ||||
| 5 | Ensemble | Ensemble | ||||
| Pairwise Comparison | Darvan Watershed | Zarrinehroud Watershed | ||||
|---|---|---|---|---|---|---|
| z | p | Significance | z | p | Significance | |
| SVM vs. RF | −2.114 | 0.005 | Yes | −2.205 | 0.000 | Yes |
| SVM vs. NB | −3.893 | 0.000 | Yes | −4.621 | 0.000 | Yes |
| SVM vs. GAM | −2.048 | 0.004 | Yes | −2.316 | 0.005 | Yes |
| SVM vs. ensemble | −2.289 | 0.000 | Yes | −2.870 | 0.000 | Yes |
| RF vs. NB | −5.766 | 0.000 | Yes | −4.478 | 0.000 | Yes |
| RF vs. GAM | −2.935 | 0.000 | Yes | −2.447 | 0.000 | Yes |
| RF vs. ensemble | −2.067 | 0.005 | Yes | −2.232 | 0.000 | Yes |
| NB vs. GAM | −3.492 | 0.000 | Yes | −4.882 | 0.000 | Yes |
| NB vs. ensemble | −3.682 | 0.000 | Yes | −3.945 | 0.000 | Yes |
| GAM vs. ensemble | −3.624 | 0.000 | Yes | −3.523 | 0.000 | Yes |
| No. | Avalanche-Affecting Factors | Percentage Increase in Mean Square Error (MSE) | |
|---|---|---|---|
| Darvan Watershed | Zarrinehroud Watershed | ||
| 1 | LS | 63.2 | 62.8 |
| 2 | Lithology | 54.6 | 55.2 |
| 3 | RSP | 41.3 | 39.8 |
| 4 | TRI | 36.5 | 37.6 |
| 5 | Slope | 32.4 | 33.4 |
| 6 | TPI | 28.2 | 29.5 |
| 7 | Profile curvature | 22.1 | 24.4 |
| 8 | Elevation | 19.8 | 21.7 |
| 9 | VRM | 17.5 | 16.5 |
| 10 | Land use | 14.7 | 14.2 |
| 11 | Aspect | 13.2 | 12.9 |
| 12 | Distance from stream | 7.3 | 8.7 |
| 13 | TWI | 5.1 | 6.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmati, O.; Ghorbanzadeh, O.; Teimurian, T.; Mohammadi, F.; Tiefenbacher, J.P.; Falah, F.; Pirasteh, S.; Ngo, P.-T.T.; Bui, D.T. Spatial Modeling of Snow Avalanche Using Machine Learning Models and Geo-Environmental Factors: Comparison of Effectiveness in Two Mountain Regions. Remote Sens. 2019, 11, 2995. https://doi.org/10.3390/rs11242995
Rahmati O, Ghorbanzadeh O, Teimurian T, Mohammadi F, Tiefenbacher JP, Falah F, Pirasteh S, Ngo P-TT, Bui DT. Spatial Modeling of Snow Avalanche Using Machine Learning Models and Geo-Environmental Factors: Comparison of Effectiveness in Two Mountain Regions. Remote Sensing. 2019; 11(24):2995. https://doi.org/10.3390/rs11242995
Chicago/Turabian StyleRahmati, Omid, Omid Ghorbanzadeh, Teimur Teimurian, Farnoush Mohammadi, John P. Tiefenbacher, Fatemeh Falah, Saied Pirasteh, Phuong-Thao Thi Ngo, and Dieu Tien Bui. 2019. "Spatial Modeling of Snow Avalanche Using Machine Learning Models and Geo-Environmental Factors: Comparison of Effectiveness in Two Mountain Regions" Remote Sensing 11, no. 24: 2995. https://doi.org/10.3390/rs11242995
APA StyleRahmati, O., Ghorbanzadeh, O., Teimurian, T., Mohammadi, F., Tiefenbacher, J. P., Falah, F., Pirasteh, S., Ngo, P. -T. T., & Bui, D. T. (2019). Spatial Modeling of Snow Avalanche Using Machine Learning Models and Geo-Environmental Factors: Comparison of Effectiveness in Two Mountain Regions. Remote Sensing, 11(24), 2995. https://doi.org/10.3390/rs11242995