3D Viewpoint Management and Navigation in Urban Planning: Application to the Exploratory Phase
Abstract
:1. Introduction
1.1. 3D Geovisualization and Urban Planning
1.2. 3D Occlusion Management Review
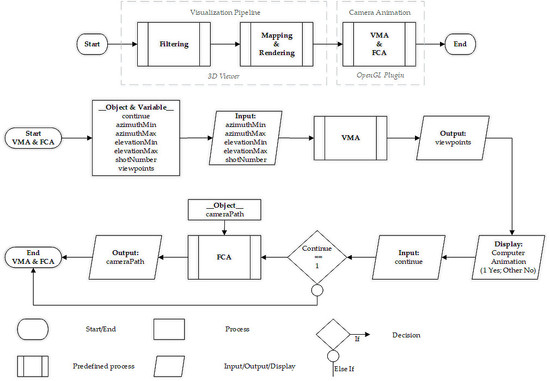
- The development of a new algorithm (flythrough creation algorithm) for producing automatic computer animations within virtual 3D geospatial models and subsequently supporting the spatial knowledge acquisition;
- The improvement of an existing viewpoint management algorithm [26] at several levels: the equal distribution of points of view on the analysis sphere, the definition of a utility function, and the framing computation of viewpoints for parallel projections. Moreover, the original algorithm has been enhanced both in calculation time and computer resources;
- The integration of the two previous algorithms within a broader semantic driven visualization process of 3D geospatial data;
- The implementation of an operational solution for automatically generating spatial bookmarks and computer animations within virtual 3D geospatial models.
2. Methodological Framework
2.1. Overview
2.2. Camera Settings
2.3. Viewpoint Management
2.3.1. Introduction
2.3.2. Method
2.4. Navigation
2.4.1. Introduction
2.4.2. Method
3. Illustration to the Virtual 3D LOD2 City Model of Brussels
3.1. Web Application
3.2. Urban Indicator
3.3. Viewpoint Management Algorithm
3.4. Flythrough Creation Algorithm
3.5. Conclusion
4. Discussion
4.1. Viewpoint Management Algorithm Complexity
4.2. Advantages
4.3. Limitations and Perspectives
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, K. Augmented Reality in Education and Training. TechTrends 2012, 56, 13–21. [Google Scholar] [CrossRef]
- Huk, T. Who benefits from learning with 3D models? The case of spatial ability: 3D-models and spatial ability. J. Comput. Assisted Learn. 2006, 22, 392–404. [Google Scholar] [CrossRef]
- Calcagno, P.; Chilès, J.P.; Courrioux, G.; Guillen, A. Geological modeling from field data and geological knowledge. Phys. Earth Planet. Interiors 2008, 171, 147–157. [Google Scholar] [CrossRef]
- Kaden, R.; Kolbe, T.H. City-wide total energy demand estimation of buildings using semantic 3d city models and statistical data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, II-2/W1, 163–171. [Google Scholar] [CrossRef]
- Pouliot, J.; Ellul, C.; Hubert, F.; Wang, C.; Rajabifard, A.; Kalantari, M.; Shojaei, D.; Atazadeh, B.; Van Oosterom, P.; De Vries, M.; et al. Visualization and New Opportunities. In Best Practices 3D Cadastre; International Federation of Surveyors: Copenhagen, Denmark, 2018; p. 77. ISBN 978-87-92853-64-6. [Google Scholar]
- Wang, C. 3D Visualization of Cadastre: Assessing the Suitability of Visual Variables and Enhancement Techniques in the 3D Model of Condominium Property Units; Université Laval: Québec, Canada, 2015. [Google Scholar]
- Milgram, P.; Kishino, F. A taxonomy of mixed reality visual displays. IEICE Trans. Inf. Syst. 1994, 77, 1321–1329. [Google Scholar]
- Kraak, M.J. Computer Assisted Cartographic Three-Dimensional Imaging Technique; Taylor & Francis: Delft, The Netherlands, 1988. [Google Scholar]
- Okoshi, T. Three-Dimensional Imaging Techniques; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- MacEachren, A.M.; Kraak, M.-J. Research Challenges in Geovisualization. Cartogr. Geogr. Inf. Sci. 2001, 28, 3–12. [Google Scholar] [CrossRef]
- Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3D City Models: State of the Art Review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842–2889. [Google Scholar] [CrossRef] [Green Version]
- Ranzinger, M.; Gleixner, G. GIS datasets for 3D urban planning. Comput. Environ. Urban Syst. 1997, 21, 159–173. [Google Scholar] [CrossRef]
- Congote, J.; Moreno, A.; Kabongo, L.; Pérez, J.-L.; San-José, R.; Ruiz, O. Web based hybrid volumetric visualisation of urban GIS data: Integration of 4D Temperature and Wind Fields with LoD-2 CityGML models. In Usage, Usability, and Utility of 3D City Model—European COST Action TU0801; Leduc, T., Moreau, G., Billen, R., Eds.; EDP Sciences: Nantes, France, 2012. [Google Scholar]
- Lu, L.; Becker, T.; Löwner, M.-O. 3D Complete Traffic Noise Analysis Based on CityGML. In Advances in 3D Geoinformation; Abdul-Rahman, A., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 265–283. ISBN 978-3-319-25689-4. [Google Scholar]
- Kaňuk, J.; Gallay, M.; Hofierka, J. Generating time series of virtual 3-D city models using a retrospective approach. Landsc. Urban Plan. 2015, 139, 40–53. [Google Scholar] [CrossRef]
- Lu, H.-C.; Sung, W.-P. Computer aided design system based on 3D GIS for park design. In Computer Intelligent Computing and Education Technology; CRC Press: London, UK, 2014; pp. 413–416. [Google Scholar]
- Moser, J.; Albrecht, F.; Kosar, B. Beyonf viusalisation—3D GIS analysis for virtual city models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, XXXVIII–4/W15, 143–146. [Google Scholar]
- Wu, H.; He, Z.; Gong, J. A virtual globe-based 3D visualization and interactive framework for public participation in urban planning processes. Comput. Environ. Urban Syst. 2010, 34, 291–298. [Google Scholar] [CrossRef]
- Calabrese, F.; Colonna, M.; Lovisolo, P.; Parata, D.; Ratti, C. Real-Time Urban Monitoring Using Cell Phones: A Case Study in Rome. IEEE Trans. Intell. Transp. Syst. 2011, 12, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Neuville, R.; Pouliot, J.; Poux, F.; De Rudder, L.; Billen, R. A Formalized 3D Geovisualization Illustrated to Selectivity Purpose of Virtual 3D City Model. ISPRS Int. J. Geo-Inf. 2018, 7, 194. [Google Scholar] [CrossRef]
- Cemellini, B.; Thompson, R.; De Vries, M.; Van Oosterom, P. Visualization/dissemination of 3D Cadastre. In FIG Congress 2018; International Federation of Surveyors: Istanbul, Turkey, 2018; p. 30. [Google Scholar]
- Ware, C. Information Visualization Perception for Design; Interactive Technologies; Elsevier Science: Burlington, NJ, USA, 2012; ISBN 0-12-381464-2. [Google Scholar]
- Li, X.; Zhu, H.; Professor, A.; Engineering, C.; Univ, T. Modeling and Visualization of Underground Structures. J. Comput. Civ. Eng. 2009, 23, 348–354. [Google Scholar] [CrossRef]
- Elmqvist, N.; Tudoreanu, M.E. Occlusion Management in Immersive and Desktop 3D Virtual Environments: Theory and Evaluation. IJVR 2007, 6, 21–32. [Google Scholar]
- Elmqvist, N.; Tsigas, P. A taxonomy of 3D occlusion management techniques. In Proceedings of the Virtual Reality Conference, Charlotte, NC, USA; 2007; pp. 51–58. [Google Scholar]
- Neuville, R.; Poux, F.; Hallot, P.; Billen, R. Towards a normalised 3D Geovisualisation: The viewpoint management. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 4, 179. [Google Scholar] [CrossRef]
- Ninger, A.K.; Bartel, S. 3D-GIS for Urban Purposes. GeoInformatica 1998, 79–103. [Google Scholar] [CrossRef]
- Semmo, A.; Trapp, M.; Jobst, M.; Döllner, J. Cartography-Oriented Design of 3D Geospatial Information Visualization—Overview and Techniques. Cartogr. J. 2015, 52, 95–106. [Google Scholar] [CrossRef]
- American Society of Civil Engineers. Glossary of the Mapping Sciences; ASCE Publications: New York, NY, USA, 1994. [Google Scholar]
- Plemenos, D. Exploring virtual worlds: Current techniques and future issues. In Proceedings of the International Conference GraphiCon, Moscow, Russia, 24–27 September 2018; 2003; pp. 5–10. [Google Scholar]
- Dutagaci, H.; Cheung, C.P.; Godil, A. A benchmark for best view selection of 3D objects. In Proceedings of the ACM Workshop on 3D Object Retrieval—3DOR ’10; ACM Press: Firenze, Italy, 2010; pp. 45–50. [Google Scholar]
- Polonsky, O.; Patané, G.; Biasotti, S.; Gotsman, C.; Spagnuolo, M. What’s in an image?: Towards the computation of the “best” view of an object. Visual Comput. 2005, 21, 840–847. [Google Scholar] [CrossRef]
- Vazquez, P.-P.; Feixas, M.; Sbert, M.; Heidrich, W. Viewpoint Selection using Viewpoint Entropy. In Proceedings of the Vision Modeling and Visualization Conference; Aka GlbH: Stuttgart, Germany, 2001; pp. 273–280. [Google Scholar]
- Lee, C.H.; Varshney, A.; Jacobs, D.W. Mesh saliency. ACM Trans. Graph. 2005, 24, 656–659. [Google Scholar] [CrossRef]
- Page, D.L.; Koschan, A.F.; Sukumar, S.R.; Roui-Abidi, B.; Abidi, M.A. Shape analysis algorithm based on information theory. In Proceedings 2003 International Conference on Image Processing (Cat. No.03CH37429); IEEE: Barcelona, Spain, 2003; Volume 1. [Google Scholar]
- Barral, P.; Dorme, G.; Plemenos, D. Visual Understanding of a Scene by Automatic Movement of a Camera. In Proceedings of the International Conference GraphiCon, Moscow, Russia, 26 August–1 September 1999. [Google Scholar]
- Snyder, J.P. Map Projections—A Working Manual; US Government Printing Office: Washington, DC, USA, 1987.
- Chittaro, L.; Burigat, S. 3D location-pointing as a navigation aid in Virtual Environments. In Proceedings of the Working Conference on Advanced Visual Interfaces—AVI ’04; ACM Press: Gallipoli, Italy, 2004; pp. 267–274. [Google Scholar]
- Darken, R.; Peterson, B. Spatial Orientation, Wayfinding, and Representation. In Handbook of Virtual Environment, 2nd ed.; CRC Press: Boca Raton, Florida, USA, 2014; pp. 467–491. ISBN 978-1-4665-1184-2. [Google Scholar] [Green Version]
- Sokolov, D.; Plemenos, D.; Tamine, K. Methods and data structures for virtual world exploration. Vis. Comput. 2006, 22, 506–516. [Google Scholar] [CrossRef]
- Häberling, C.; Bär, H.; Hurni, L. Proposed Cartographic Design Principles for 3D Maps: A Contribution to an Extended Cartographic Theory. Cartographica 2008, 43, 175–188. [Google Scholar] [CrossRef]
- Jaubert, B.; Tamine, K.; Plemenos, D. Techniques for off-line scene exploration using a virtual camera. In Proceedings of the International Conference 3IA, Limoges, France, 23–24 May 2006; 2006; p. 14. [Google Scholar]
- Poux, F.; Neuville, R.; Hallot, P.; Van Wersch, L.; Luczfalvy Jancsó, A.; Billen, R. Digital Investigations of an Archaeological Smart Point Cloud: A Real Time Web-Based Platform to Manage the Visualisation of Semantical Queries. In Conservation of Cultural Heritage in the Digital Era; ISPRS: Florence, Italy, 2017; pp. 581–588. [Google Scholar]
- DiCarlo, J.J.; Zoccolan, D.; Rust, N.C. How Does the Brain Solve Visual Object Recognition? Neuron 2012, 73, 415–434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baddeley, A.D.; Kopelman, M.D.; Wilson, B.A. The Handbook of Memory Disorders. John Wiley & Sons: Chichester, UK, 2002; ISBN 0-471-49819-X. [Google Scholar]
- Tjan, B.S.; Legge, G.E. The viewpoint complexity of an object-recognition task. Vis. Res. 1998, 38, 2335–2350. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Wang, L.; Zhou, W.; Zhang, H.; Cui, X.; Guo, Y. Viewpoint Selection for Photographing Architectures. arXiv, 2017; arXiv:1703.01702. [Google Scholar]
- Cemellini, B.; Thompson, R.; Oosterom, P.V. Usability testing of a web-based 3D Cadastral visualization system. In Proceedings of the 6th International FIG Workshop on 3D Cadastres, Delft, The Netherlands, 1–5 October 2018; p. 20. [Google Scholar]
- Poux, F.; Neuville, R.; Van Wersch, L.; Nys, G.-A.; Billen, R. 3D Point Clouds in Archaeology: Advances in Acquisition, Processing and Knowledge Integration Applied to Quasi-Planar Objects. Geosciences 2017, 7, 96. [Google Scholar] [CrossRef]
- Poux, F.; Neuville, R.; Nys, G.-A.; Billen, R. 3D Point Cloud Semantic Modeling: Integrated Framework for Indoor Spaces and Furniture. Remote Sens. 2018, 10, 1412. [Google Scholar] [CrossRef]














| Design Pattern | Signification | Example |
|---|---|---|
| Multiple viewports | Managing occlusion with two or more views (overview and detailed view(s)) | Tumbler, worldlets |
| Virtual X-ray | Managing occlusion in the image-space through fragment shaders | Perspective cutouts, image-space dynamic transparency |
| Tour planner | Managing occlusion with an exploration phase | Way-finder |
| Interactive exploder | Managing occlusion in the object-space through user’s interaction | 3D explosion probe, deformation-based volume explosion |
| Projection distorter | Managing occlusion in the view-space through two or more integrated views | Artistic multiprojection, view projection animation |
| P1/P1Max | P2/P2Max | P3/P3Max | P4/P4Max | P5/P5Max | P6/P6Max | P7/P7Max | P8/P8Max | P9/P9Max | Sum | |
|---|---|---|---|---|---|---|---|---|---|---|
| Viewpoint1 | 0.278 | 0.350 | 0.300 | 0.440 | 0.387 | 0.103 | 0.264 | 0.376 | 0.390 | 2.888 |
| Viewpoint2 | 0.291 | 0.390 | 0.350 | 0.522 | 0.413 | 0.144 | 0.315 | 0.434 | 0.470 | 3.329 |
| Viewpoint3 | 0.278 | 0.388 | 0.349 | 0.529 | 0.386 | 0.134 | 0.329 | 0.437 | 0.486 | 3.316 |
| Viewpoint4 | 0.353 | 0.329 | 0.412 | 0.543 | 0.315 | 0.330 | 0.280 | 0.336 | 0.363 | 3.261 |
| Viewpoint5 | 0.341 | 0.330 | 0.422 | 0.415 | 0.288 | 0.353 | 0.295 | 0.303 | 0.364 | 3.111 |
| … | … | … | … | … | … | … | … | … | … | … |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neuville, R.; Pouliot, J.; Poux, F.; Billen, R. 3D Viewpoint Management and Navigation in Urban Planning: Application to the Exploratory Phase. Remote Sens. 2019, 11, 236. https://doi.org/10.3390/rs11030236
Neuville R, Pouliot J, Poux F, Billen R. 3D Viewpoint Management and Navigation in Urban Planning: Application to the Exploratory Phase. Remote Sensing. 2019; 11(3):236. https://doi.org/10.3390/rs11030236
Chicago/Turabian StyleNeuville, Romain, Jacynthe Pouliot, Florent Poux, and Roland Billen. 2019. "3D Viewpoint Management and Navigation in Urban Planning: Application to the Exploratory Phase" Remote Sensing 11, no. 3: 236. https://doi.org/10.3390/rs11030236
APA StyleNeuville, R., Pouliot, J., Poux, F., & Billen, R. (2019). 3D Viewpoint Management and Navigation in Urban Planning: Application to the Exploratory Phase. Remote Sensing, 11(3), 236. https://doi.org/10.3390/rs11030236