Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. Image Acquisition and Preprocessing
2.3. Ground Reference Data Acquisition
3. Methodology
3.1. Image Segmentation
3.1.1. Unsupervised Optimal SP Selection Method
3.1.2. Supervised Optimal SP Selection Method
3.2. Feature Calculation
3.3. Optimal Feature Subset Selection
3.4. Parameter Optimization of Machine-Learning Classification Algorithms for Crop Recognition
4. Results and Discussion
4.1. Optimal SP Selection and Image Segmentation
4.2. Feature Calculation and Optimal Feature Subset Selection
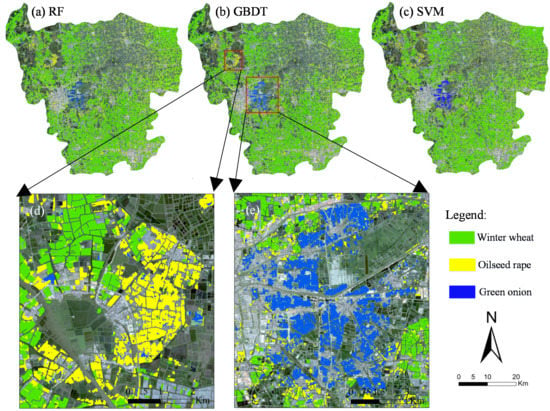
4.3. Crop Classification and Accuracy Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| R: = remaining feature set which contains n features initially |
| S: = the score of a criterion function for a particular feature set, e.g. the accuracy of 4-fold cross validation |
| Sset: = the dataset which contains the scores of each iteration of R, initialize Sset = ∅ |
| k: the number of remaining features, initialize k = n |
| d: = search depth,1 < d < n |
| START: |
| Step 1: Train a model of RF, GBDT or SVM based on R, calculate the score S1 and the importance of features in R, append S1 at the end of Sset. |
| Step 2: Rank features in R based on importance from the lowest to the highest, R= {f1, f2, f3, …, fk } |
| Step 3: m = min(d, k) |
| For i = 1 to m: |
| Construct a new feature set Ri by removing the feature fi from R. |
| Train a model on the samples with the remaining features in Ri and calculate the score of Si. |
| Re-rank features in Ri based on importance from the lowest to the highest Ri = { f1, f2, f3, …, fk−1}. |
| EndFor |
| Step 4: Set Sj = max(Si), and R = Rj, k = k − 1, append Sj to the end of Sset. |
| Step 5: Repeat steps 3~4 until R = ∅ |
| Step 6: Select the feature subset R with the highest score S in Sset as the optimal feature subset |
| END. |
Appendix B
| Classification Method | Object Class | Winter Wheat | Oilseed Rape | Green Onion | Others | User’s Accuracy (%) |
|---|---|---|---|---|---|---|
| RF | Winter wheat | 193 | 5 | 0 | 5 | 95.1 |
| Oilseed rape | 0 | 49 | 3 | 7 | 83.1 | |
| Green onion | 0 | 1 | 38 | 1 | 95.0 | |
| Others | 2 | 14 | 12 | 278 | 90.8 | |
| Producer’s accuracy (%) | 99.0 | 71.0 | 71.7 | 95.5 | - | |
| Overall accuracy (%) | 91.8 | - | Kappa coefficient | 0.871 | - | |
| GBDT | Winter wheat | 192 | 4 | 1 | 9 | 93.2 |
| Oilseed rape | 0 | 55 | 4 | 8 | 82.1 | |
| Green onion | 1 | 2 | 41 | 0 | 93.2 | |
| Others | 2 | 8 | 7 | 274 | 94.2 | |
| Producer’s accuracy (%) | 98.5 | 79.7 | 77.4 | 94.1 | - | |
| Overall accuracy (%) | 92.4 | - | Kappa coefficient | 0.882 | - | |
| SVM | Winter wheat | 189 | 9 | 0 | 10 | 90.9 |
| Oilseed rape | 1 | 47 | 2 | 15 | 72.3 | |
| Green onion | 0 | 4 | 49 | 1 | 90.7 | |
| Others | 5 | 9 | 2 | 265 | 94.3 | |
| Producer’s accuracy (%) | 96.9 | 68.1 | 92.5 | 91.1 | - | |
| Overall accuracy (%) | 90.5 | - | Kappa coefficient | 0.853 | - |
References
- Godfray, H.C.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812. [Google Scholar] [CrossRef] [PubMed]
- Morton, D.C.; Defries, R.S.; Nagol, J.; Souza, C.M., Jr.; Nagol, J.; Kasischke, E.S.; Hurtt, G.C.; Dubayah, R. Mapping canopy damage from understory fires in Amazon forests using annual time series of Landsat and MODIS data. Remote Sens. Environ. 2011, 115, 1706–1720. [Google Scholar] [CrossRef] [Green Version]
- Mansaray, L.; Huang, W.; Zhang, D.; Huang, J.; Li, J. Mapping Rice Fields in Urban Shanghai, Southeast China, Using Sentinel-1A and Landsat 8 Datasets. Remote Sens. 2017, 9, 257. [Google Scholar] [CrossRef]
- Sharma, R.C.; Hara, K.; Tateishi, R. High-Resolution Vegetation Mapping in Japan by Combining Sentinel-2 and Landsat 8 Based Multi-Temporal Datasets through Machine Learning and Cross-Validation Approach. Land 2017, 6, 50. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef] [Green Version]
- Novelli, A.; Aguilar, M.A.; Nemmaoui, A.; Aguilar, F.J.; Tarantino, E. Performance evaluation of object based greenhouse detection from Sentinel-2 MSI and Landsat 8 OLI data: A case study from Almeria (Spain). Int. J. Appl. Earth Obs. 2016, 52, 403–411. [Google Scholar] [CrossRef]
- Zhou, W.Q.; Huang, G.L.; Troy, A.; Cadenasso, M.L. Object-based land cover classification of shaded areas in high spatial resolution imagery of urban areas: A comparison study. Remote Sens. Environ. 2009, 113, 1769–1777. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Granger, J.; Brisco, B. Wetland classification in Newfoundland and Labrador using multi-source SAR and optical data integration. GISci. Remote Sens. 2017, 54, 779–796. [Google Scholar] [CrossRef]
- Kussul, N.; Lemoine, G.; Gallego, F.J.; Skakun, S.V. Parcel-Based Crop Classification in Ukraine Using Landsat-8 Data and Sentinel-1A Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 9, 2500–2508. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Wang, L.; Sousa, W.P.; Gong, P. Integration of object-based and pixel-based classification for mapping mangroves with IKONOS imagery. Int. J. Remote Sens. 2004, 25, 5655–5668. [Google Scholar] [CrossRef]
- Jobin, B.; Labrecque, S.; Grenier, M.; Falardeau, G. Object-Based Classification as an Alternative Approach to the Traditional Pixel-Based Classification to Identify Potential Habitat of the Grasshopper Sparrow. Environ. Manag. 2008, 41, 20–31. [Google Scholar] [CrossRef] [PubMed]
- Byun, Y.G. A multispectral image segmentation approach for object-based image classification of high resolution satellite imagery. KSCE J. Civ. Eng. 2013, 17, 486–497. [Google Scholar] [CrossRef]
- Coillie, F.M.B.V.; Verbeke, L.P.C.; Wulf, R.R.D. Feature selection by genetic algorithms in object-based classification of IKONOS imagery for forest mapping in Flanders, Belgium. Remote Sens. Environ. 2007, 110, 476–487. [Google Scholar]
- Huang, Y.; Zhao, C.; Yang, H.; Song, X.; Chen, J.; Li, Z. Feature Selection Solution with High Dimensionality and Low-Sample Size for Land Cover Classification in Object-Based Image Analysis. Remote Sens. 2017, 9, 939. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I.; Yomralioglu, T. Object-based classification with rotation forest ensemble learning algorithm using very-high-resolution WorldView-2 image. Remote Sens. Lett. 2015, 6, 834–843. [Google Scholar] [CrossRef]
- Cánovasgarcía, F.; Alonsosarría, F. Optimal Combination of Classification Algorithms and Feature Ranking Methods for Object-Based Classification of Submeter Resolution Z/I-Imaging DMC Imagery. Remote Sens. 2015, 7, 4651–4677. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Jia, K.; Li, X.; Yuan, Q.; Zhao, X. Multi-scale segmentation approach for object-based land-cover classification using high-resolution imagery. Remote Sens. Lett. 2014, 5, 73–82. [Google Scholar] [CrossRef]
- Liu, D.; Xia, F. Assessing object-based classification: Advantages and limitations. Remote Sens. Lett. 2009, 1, 187–194. [Google Scholar] [CrossRef]
- Ma, L.; Cheng, L.; Li, M.; Liu, Y.; Ma, X. Training set size, scale, and features in Geographic Object-Based Image Analysis of very high resolution unmanned aerial vehicle imagery. ISPRS J. Photogramm. Remote Sens. 2015, 102, 14–27. [Google Scholar] [CrossRef]
- Chen, X.W.; Jeong, J.C. Enhanced Recursive Feature Elimination. In Proceedings of the International Conference on Machine Learning and Applications, Cincinnati, OH, USA, 13–15 December 2007; pp. 429–435. [Google Scholar]
- Laliberte, A.S.; Browning, D.M.; Rango, A. A comparison of three feature selection methods for object-based classification of sub-decimeter resolution UltraCam-L imagery. Int. J. Appl. Earth Observ. Geoinf. 2012, 15, 70–78. [Google Scholar] [CrossRef]
- Li, L.; Solana, C.; Canters, F.; Kervyn, M. Testing random forest classification for identifying lava flows and mapping age groups on a single Landsat 8 image. J. Volcanol. Geotherm. Res. 2017, 345, 109–124. [Google Scholar] [CrossRef]
- Buddhiraju, K.M.; Rizvi, I.A. Comparison of CBF, ANN and SVM classifiers for object based classification of high resolution satellite images. In Proceedings of the Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 40–43. [Google Scholar]
- Bhaskaran, S.; Paramananda, S.; Ramnarayan, M. Per-pixel and object-oriented classification methods for mapping urban features using Ikonos satellite data. Appl. Geogr. 2010, 30, 650–665. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Rango, A.; Havstad, K.M.; Paris, J.F.; Beck, R.F.; Mcneely, R.; Gonzalez, A.L. Object-oriented image analysis for mapping shrub encroachment from 1937 to 2003 in southern New Mexico. Remote Sens. Environ. 2004, 93, 198–210. [Google Scholar] [CrossRef]
- Kim, M.; Madden, M.; Warner, T. Estimation of optimal image object size for the segmentation of forest stands with multispectral IKONOS imagery. In Object-Based Image Analysis; Springer: Berlin/Heidelberg, Germany, 2008; pp. 291–307. [Google Scholar]
- Rau, J.Y.; Jhan, J.P.; Rau, R.J. Semiautomatic Object-Oriented Landslide Recognition Scheme From Multisensor Optical Imagery and DEM. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1336–1349. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Möller, M.; Lymburner, L.; Volk, M. The comparison index: A tool for assessing the accuracy of image segmentation. Int. J. Appl. Earth Observ. Geoinf. 2007, 9, 311–321. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy Assessment Measures for Object-based Image Segmentation Goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Gao, H.; Tang, Y.; Jing, L.; Li, H.; Ding, H. A Novel Unsupervised Segmentation Quality Evaluation Method for Remote Sensing Images. Sensors 2017, 17, 2427. [Google Scholar] [CrossRef] [PubMed]
- Kalantar, B.; Mansor, S.B.; Sameen, M.I.; Pradhan, B.; Shafri, H.Z.M. Drone-based land-cover mapping using a fuzzy unordered rule induction algorithm integrated into object-based image analysis. Int. J. Remote Sens. 2017, 38, 2535–2556. [Google Scholar] [CrossRef]
- Mellor, A.; Haywood, A.; Jones, S.; Wilkes, P. Forest Classification using Random forests with multisource remote sensing and ancillary GIS data. In Proceedings of the Australian Remote Sensing and Photogrammetry Conference, Melbourne, Australia, 27–28 August 2012. [Google Scholar]
- Costa, H.; Foody, G.M.; Boyd, D.S. Supervised methods of image segmentation accuracy assessment in land cover mapping. Remote Sens. Environ. 2018, 205, 338–351. [Google Scholar] [CrossRef]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. Image segmentation evaluation: A survey of unsupervised methods. Comput. Vis. Image Understand. 2008, 110, 260–280. [Google Scholar] [CrossRef] [Green Version]
- Kaya, G.T.; Torun, Y.; Küçük, C. Recursive feature selection based on non-parallel SVMs and its application to hyperspectral image classification. In Proceedings of the Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3558–3561. [Google Scholar]
- Cintra, M.E.; Camargo, H.A. Feature Subset Selection for Fuzzy Classification Methods; Springer: Berlin/Heidelberg, Germany, 2010; pp. 318–327. [Google Scholar]
- Han, Y.; Yu, L. A Variance Reduction Framework for Stable Feature Selection. Stat. Anal. Data Min. 2012, 5, 428–445. [Google Scholar] [CrossRef]
- Khair, N.M.; Hariharan, M.; Yaacob, S.; Basah, S.N. Locality sensitivity discriminant analysis-based feature ranking of humanemotion actions recognition. J. Phys. Therapy Sci. 2015, 27, 2649–2653. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Chen, C.; Kechadi, T.M.; Sun, L. comparative evaluation of filter-based feature selection methods for hyper-spectral band selection. Int. J. Remote Sens. 2013, 34, 7974–7990. [Google Scholar] [CrossRef]
- Mursalin, M.; Zhang, Y.; Chen, Y.; Chawla, N.V. Automated Epileptic Seizure Detection Using Improved Correlation-based Feature Selection with Random Forest Classifier. Neurocomputing 2017, 241, 204–214. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.; Lin, C. LIBSVM: A library for support vector machines. ACM Trans. Intel. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Guyon, I. Erratum: Gene selection for cancer classification using support vector machines. Mach. Learn. 2001, 46, 389–422. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.; Stone, C.J. Classification and Regression Trees. Encycl. Ecol. 1984, 57, 582–588. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Liu, T.; Abdelrahman, A. An Object-Based Image Analysis Method for Enhancing Classification of Land Covers Using Fully Convolutional Networks and Multi-View Images of Small Unmanned Aerial System. Remote Sens. 2018, 10, 457. [Google Scholar] [CrossRef]
- Ma, L.; Fu, T.; Blaschke, T.; Li, M.; Tiede, D.; Zhou, Z.; Ma, X.; Chen, D. Evaluation of Feature Selection Methods for Object-Based Land Cover Mapping of Unmanned Aerial Vehicle Imagery Using Random Forest and Support Vector Machine Classifiers. ISPRS Int. J. Geo-Inf. 2017, 6, 51. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Li, H.; Wang, J.; Huang, W. A study on classification and monitoring of winter wheat growth status by Landsat/TM image. J. Triticeae Crops 2010, 30, 92–95. [Google Scholar]
- Liu, J.; Zhu, W.; Sun, G.; Zhang, J.; Jiang, N. Endmember abundance calibration method for paddy rice area extraction from MODIS data based on independent component analysis. Trans. Chin. Soc. Agric. Eng. 2012, 28, 103–108. [Google Scholar]
- Xue, Y.; Li, J. Year-round production technology of green onion in Xinhua. Shanghai Vegetables 2012, 6, 28–29. [Google Scholar]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. Geosci. Remote Sens. IEEE Trans. 2002, 35, 675–686. [Google Scholar] [CrossRef]
- Liu, J.; Wang, L.; Yang, L.; Shao, J.; Teng, F.; Yang, F.; Fu, C. Geometric correction of GF-1 satellite images based on block adjustment of rational polynomial model. Trans. Chin. Soc. Agric. Eng. 2015, 31, 146–154. [Google Scholar]
- Martha, T.R.; Kerle, N.; Westen, C.J.V.; Jetten, V.; Kumar, K.V. Segment Optimization and Data-Driven Thresholding for Knowledge-Based Landslide Detection by Object-Based Image Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Combining object-based texture measures with a neural network for vegetation mapping in the Everglades from hyperspectral imagery. Remote Sens. Environ. 2012, 124, 310–320. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. Isprs J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Böck, S.; Immitzer, M.; Atzberger, C. On the objectivity of the objective function—Problems with unsupervised segmentation evaluation based on global score and a possible remedy. Remote Sens. 2017, 9, 769. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. Syst. Man Cybern. IEEE Trans. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Rouse, J.W.J.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Jurgens, C. The modified normalized difference vegetation index (mNDVI) a new index to determine frost damages in agriculture based on Landsat TM data. Int. J. Remote Sens. 1997, 18, 3583–3594. [Google Scholar] [CrossRef]
- Reif, M.; Shafait, F.; Dengel, A. Meta-Learning for Evolutionary Parameter Optimization of Classifiers. Mach. Learn. 2012, 87, 357–380. [Google Scholar] [CrossRef]
- Chopra, T.; Vajpai, J. Fault Diagnosis in Benchmark Process Control System Using Stochastic Gradient Boosted Decision Trees. Int. J. Soft Comput. Eng. 2011, 1, 98–101. [Google Scholar]
- Liu, L.; Ji, M.; Buchroithner, M. Combining Partial Least Squares and the Gradient-Boosting Method for Soil Property Retrieval Using Visible Near-Infrared Shortwave Infrared Spectra. Remote Sens. 2017, 9, 1299. [Google Scholar] [CrossRef]
- Cherkassky, V. The nature of statistical learning theory. IEEE Trans. Neural Netw. 2002, 38, 409. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.N.; Yang, J.G.; Zhong, Y.W.; Deng, C. Multi-class SVM based remote sensing image classification and its semi-supervised improvement scheme. In Proceedings of the International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; pp. 3146–3151. [Google Scholar]
- HAY, A.M. The derivation of global estimates from a confusion matrix. Int. J. Remote Sens. 1988, 9, 1395–1398. [Google Scholar] [CrossRef]
- Bai, Y.; Sun, X.; Tian, M.; Fuller, A.M. Typical Water-Land Utilization GIAHS in Low-Lying Areas: The Xinghua Duotian Agrosystem Example in China. J. Resour. Ecol. 2014, 5, 320–327. [Google Scholar]
- Chi, M.; Rui, F.; Bruzzone, L. Classification of hyperspectral remote-sensing data with primal SVM for small-sized training dataset problem. Adv. Space Res. 2008, 41, 1793–1799. [Google Scholar] [CrossRef]
- Yu, Y.; McKelvey, T.; Kung, S. A classification scheme for ‘high-dimensional-small-sample-size’ data using soda and ridge-SVM with microwave measurement applications. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 3542–3546. [Google Scholar]
- Samadzadegan, F.; Hasani, H.; Schenk, T. Simultaneous feature selection and SVM parameter determination in classification of hyperspectral imagery using Ant Colony Optimization. Can. J. Remote Sens. 2012, 38, 139–156. [Google Scholar] [CrossRef]
- Mao, Q.H.; Ma, H.W.; Zhang, X.H. SVM Classification Model Parameters Optimized by Improved Genetic Algorithm. Adv. Mater. Res. 2014, 889–890, 617–621. [Google Scholar] [CrossRef]
- Poursanidis, D.; Topouzelis, K.; Chrysoulakis, N. Mapping coastal marine habitats and delineating the deep limits of the Neptune’s seagrass meadows using very high resolution Earth observation data. Int. J. Remote Sens. 2018, 39, 8670–8687. [Google Scholar] [CrossRef]












| Method | 30 Features Selected in Order of Feature Importance |
|---|---|
| RF | EVI_0429, EVI_0518, NDVI_1207, LSWI_0429, NDVI_0429, EVI_0315, EVI_0127, WNDWI_0429, B1_MEAN_0429, NDVI_0518, WNDWI_0518, EVI_0228, GLCM_MEAN_0228, Area, B8_MEAN_0228, LSWI_0518, LSWI_0315, B5_MEAN_0518, B1_MEAN_1207, WNDWI_0228, B1_MEAN_0228, GLCM_Homogeneit_0429, B10_MEAN_0228, Length, B6_MEAN_0429, B8_MEAN_0429, B6_MEAN_0518, NDVI_0315, B2_Std_0228, GLCM_Contrast_0228 |
| GBDT | EVI_0429, EVI_1207, B1_MEAN_0429, EVI_0518, EVI_0315, B10_MEAN_0228, NDVI_1207, GLCM_Correlation_0228, Length, B5_MEAN_0518, B8_MEAN_0228, LSWI_0315, B6_MEAN_0315, B7_MEAN_0429, LSWI_0518, GLCM_MEAN_0228, LSWI_0429, WNDWI_0429, B1_MEAN_1207, NDVI_0315, EVI_0228, WNDWI_0228, Area, B2_MEAN_0518, GLCM_Homogeneit_0429, B5_MEAN_0429, B1_MEAN_0315, B1_Std_1207, B3_MEAN_1207,NDVI_0518 |
| SVM | EVI_0429, EVI_1207, LSWI_0315, B1_MEAN_1207, NDVI_1207, EVI_0518, EVI_0127, EVI_0228, GLCM_Mean_0228, B4_MEAN_1207, B3_MEAN_1207, WNDWI_0429, EVI_0315, Area, LSWI_0518, B5_MEAN_0518, B8_Mean_0228, NDVI_0228, B1_Std_1207, WNDWI_0315, NDVI_0315, GLCM_entropy_1207, LSWI_0429, B10_MEAN_0429, GLCM_Homogeneit_0429, B7_MEAN_0518, B10_MEAN_0228, Length, B2_MEAN_1207, GLCM_Correlation_0315 |
| Feature Selection Algorithm | Classification Method | ||
|---|---|---|---|
| RF | GBDT | SVM | |
| RFE | 258.45 s | 122.73 s | 24712.55 s |
| EnRFE | 1955.22 s | 1284.21 s | 158432.64 s |
| iEnRFE | 651.75 s | 485.73 s | 52132.63 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Mansaray, L.R.; Huang, J.; Wang, L. Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery. Remote Sens. 2019, 11, 514. https://doi.org/10.3390/rs11050514
Yang L, Mansaray LR, Huang J, Wang L. Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery. Remote Sensing. 2019; 11(5):514. https://doi.org/10.3390/rs11050514
Chicago/Turabian StyleYang, Lingbo, Lamin R. Mansaray, Jingfeng Huang, and Limin Wang. 2019. "Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery" Remote Sensing 11, no. 5: 514. https://doi.org/10.3390/rs11050514
APA StyleYang, L., Mansaray, L. R., Huang, J., & Wang, L. (2019). Optimal Segmentation Scale Parameter, Feature Subset and Classification Algorithm for Geographic Object-Based Crop Recognition Using Multisource Satellite Imagery. Remote Sensing, 11(5), 514. https://doi.org/10.3390/rs11050514