An Uncertainty Quantified Fundamental Climate Data Record for Microwave Humidity Sounders
Abstract
:1. Introduction
2. Data and Methods
2.1. Microwave Radiometer Data
2.2. Methods
2.2.1. Measurement Equation Approach
2.2.2. Improvements Compared to AAPP
Antenna Pattern Correction (APC)
Band Correction
Usage of PRT No. 6 for AMSU-B
Radio Frequency Interference (RFI)
Accurate Value for Cosmic Microwave Background ()
2.2.3. Uncertainty Model
3. Results
3.1. Comparing the Initial and Final Implementation to AAPP
3.2. FCDR Example Contents
3.3. Assessment of Uncertainties
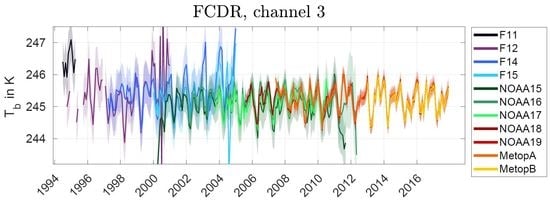
3.4. Inter-Satellite Comparison: Improvements in the FCDR
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AAPP | ATOVS and AVHRR Pre-processing Package |
| AMSU-B | Advanced Microwave Sounding Unit -B |
| APC | antenna pattern correction |
| ATOVS | Advanced TIROS-N Operational Vertical Sounder |
| AVHRR | Advanced Very High Resolution Radiometer |
| CDR | climate data record |
| DMSP | Defense Meteorological Satellite Program |
| DSV | deep space view |
| ECV | essential climate variable |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| FCDR | fundamental climate data record |
| FIDUCEO | Fidelity and uncertainty in climate data records from Earth observation |
| IWCT | internal warm calibration target |
| LECT | local equator crossing time |
| MHS | Microwave Humidity Sounder |
| MW | microwave |
| NET | Noise equivalent differential temperature |
| NetCDF | Network Common Data Format |
| NOAA CLASS | NOAA—Comprehensive Large Array-data Stewardship System |
| NOAA NCEI | NOAA—National Centers for Environmental Information |
| NWP | numerical weather prediction |
| RFI | radio frequency interference |
| SNO | simultaneous nadir overpass |
| SSM/I | Special Sensor Microwave Imager |
| SSMT-2 | Special Sensor Microwave Water Vapor Profiler |
| UTH | upper tropospheric humidity |
Appendix A





References
- John, V.O.; Allan, R.P.; Bell, B.; Buehler, S.A.; Kottayil, A. Assessment of inter-calibration methods for satellite microwave humidity sounders. J. Geophys. Res. 2013, 118, 4906–4918. [Google Scholar] [CrossRef]
- Hanlon, H.; Ingram, W. Algorithm Theoretical Basis Document, Fundamental Climate Data Record of Microwave Brightness Temperatures, CF-26/27/28, version 1.0; Technical Report SAF/CM/UKMO/ATBD/FCDR_MWAVE; Satellite Application Facility on Climate Monitoring (CM SAF), 2016. Available online: www.cmsaf.eu (accessed on 6 March 2019).
- Ferraro, R. AMSU-B/MHS Brightness Temperature—Climate Algorithm Theoretical Basis Document, NOAA Climate Data Record Program CDRP-ATBD-0801 Rev. 1; Technical report; NOAA STAR: College Park, MD, USA, 2016.
- Zou, C.Z.; Goldberg, M.D.; Cheng, Z.; Grody, N.C.; Sullivan, J.T.; Tarpley, D. Recalibration of microwave sounding unit for climate studies using simultaneous nadir overpasses. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Moradi, I.; Beauchamp, J.; Ferraro, R. Radiometric correction of observations from microwave humidity sounders. Atmos. Meas. Tech. 2018, 11, 6617–6626. [Google Scholar] [CrossRef]
- Chung, E.S.; Soden, B.J.; John, V.O. Intercalibrating microwave satellite observations for monitoring long-term variations in upper and mid-tropospheric water vapor. J. Atmos. Ocean. Technol. 2013, 30, 2303–2319. [Google Scholar] [CrossRef]
- Shi, L.; Bates, J.J. Three decades of intersatellite-calibrated High-Resolution Infrared Radiation Sounder upper tropospheric water vapor. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Chung, E.S.; Soden, B.J.; Huang, X.; Shi, L.; John, V.O. An assessment of the consistency between satellite measurements of upper tropospheric water vapor. J. Geophys. Res. 2016, 121, 2874–2887. [Google Scholar] [CrossRef]
- Wentz, F.J.; Mears, C.A.; Program, N.C. NOAA Climate Data Record (CDR) of SSM/I and SSMIS Microwave Brightness Temperatures, RSS Version 7; NOAA National Centers for Environmental Information: Silver Spring, MD, USA, 2013. [CrossRef]
- Kummerow, C.D.; Berg, W.K.; Sapiano, M.R.P.; Program, N.C. NOAA Climate Data Record (CDR) of SSM/I and SSMIS Microwave Brightness Temperatures, CSU Version 1; NOAA National Climatic Data Center: Silver Spring, MD, USA, 2013.
- Berg, W.; Kroodsma, R.; Kummerow, C.D.; McKague, D.S. Fundamental Climate Data Records of Microwave Brightness Temperatures. Remote Sens. 2018, 10, 1306. [Google Scholar] [CrossRef]
- Fennig, K.; Schröder, M.; Hollmann, R. Fundamental Climate Data Record of Microwave Imager Radiances; Satellite Application Facility on Climate Monitoring (CM SAF), 2017, 3rd ed. Available online: www.cmsaf.eu (accessed on 3 March 2019).
- Zou, C.Z.; Wang, W. Intersatellite calibration of AMSU-A observations for weather and climate applications. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Mo, T. Inter-satellite calibration of the NOAA AMSU-A measurements over tropical oceans. Remote Sens. Environ. 2014, 149, 205–212. [Google Scholar] [CrossRef]
- Chander, G. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- NOAA. NOAA KLM User’s Guide with NOAA-N, -N’ Supplement; Technical Report; National Oceanic and Atmospheric Administration, National Environmental Satellite, Data, and Information Service, National Climatic Data Center, Remote Sensing and Applications Division, 2009. Available online: https://www.noaa.gov/ (accessed on 6 March 2019).
- Kobayashi, S.; Poli, P.; John, V.O. Characterisation of Special Sensor Microwave Water Vapor Profiler (SSM/T-2) radiances using radiative transfer simulations from global atmospheric reanalyses. Adv. Space Res. 2016, 59, 917–935. [Google Scholar] [CrossRef]
- Labrot, T.; Lavanant, L.; Whyte, K.; Atkinson, N.; Brunel, P. AAPP Documentation Scientific Description, Version 6.0, Document NWPSAF-MF-UD-001; Technical Report. NWP SAF, Satellite Application Facility for Numerical Weather Prediction, 2006. Available online: https://www.nwpsaf.eu/site/ (accessed on 6 March 2019).
- Woolliams, E.; Mittaz, J.; Merchant, C.J.; Harris, P. D2.2a: Principles Behind the FCDR Effects Tables; Technical Report. National Physical Laboratory and University of Reading, 2017. Available online: www.npl.co.uk/ (accessed on 6 March 2019).
- Saunders, R.W.; Hewison, T.J.; Stringer, S.J.; Atkinson, N.C. The Radiometric Characterization of AMSU-B. IEEE Trans. Microw. Theory Tech. 1995, 43, 760–771. [Google Scholar] [CrossRef]
- Hewison, T.J.; Saunders, R. Measurements of the AMSU-B Antenna Pattern. IEEE Trans. Geosci. Remote Sens. 1996, 34, 405–412. [Google Scholar] [CrossRef]
- Klaes, D.; Ackermann, J. Techniques and Processes for Pre-Launch Characterisation of New Instruments; Technical Report. EUMETSAT, 2014. Available online: https://www.eumetsat.int/ (accessed on 6 March 2019).
- Atkinson, N.C.; McLellan, S. Initial evaluation of AMSU-B in-orbit data. Proce. SPIE Int. Soc. Opt. Eng. 1998, 3503, 276–287. [Google Scholar] [CrossRef]
- Atkinson, N.C. Performance of AMSU-B Flight Model 2 (FM2) During NOAA-L Post Launch Orbital Verification Tests, AMB112; Technical Report; Remote Sensing Instrumentation, Met Office: Exeter, UK, 2000.
- Atkinson, N.C. Performance of AMSU-B Flight Model 3 (FM3) During NOAA-M Post Launch Orbital Verification Tests, AMB113; Technical Report; Remote Sensing Instrumentation, Met Office: Exeter, UK, 2002.
- Hewison, T.J. A Thermal Model of Black Body Targets; Met Office (RS) Working Paper No. 29, August 1991; Met Office: Exeter, UK; Farnborough, UK, 1991; 12p.
- JPSS ATMS SDR Science Team. Joint Polar Satellite System (JPSS) Advanced Technology Microwave Sounder (ATMS) SDR Calibration Algorithm Theoretical Basis Document (ATBD); Technical Report; NOAA Center for Sattelite Application and Research: Silver Spring, MD, USA, 2013.
- Burgdorf, M.; Hans, I.; Prange, M.; Mittaz, J.; Woolliams, E. D2.2 Microwave: Report on the MW FCDR Uncertainty; Technical Report; Universität Hamburg, National Physical Laboratory: Hamburg, Germany, 2017. [Google Scholar]
- Khan, S.; Shaw, G. PFM Radiometric Calibration Test Report, MHS-TR-JA281-MMP; Technical Report; MATRA MARCONI SPACE UK Limited: Paris, France, 1999. [Google Scholar]
- Atkinson, N.C. Calibration, monitoring and validation of AMSU-B. Adv. Space Res. 2001, 28, 117–126. [Google Scholar] [CrossRef]
- John, V.O.; Holl, G.; Atkinson, N.; Buehler, S.A. Monitoring scan asymmetry of microwave humidity sounding channels using simultaneous all angle collocations (SAACs). J. Geophys. Res. 2013, 118, 1536–1545. [Google Scholar] [CrossRef] [Green Version]
- Hans, I.; Burgdorf, M.; Buehler, S.A. On-board radio frequency interference as origin of inter-satellite biases for microwave humidity sounders. Unpublished, in preparation.
- Hans, I.; Burgdorf, M.; Woolliams, E. Product User Guide—Microwave FCDR Release 4.1; Techreport; Universität Hamburg and National Physical Laboratory: Hamburg, Germany, 2019. [Google Scholar]
- Fixsen, D.J. The temperature of the cosmic microwave background. Astrophys. J. 2009, 707. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology (JCGM). Evaluation of Measurement Data—Guide to the Expression Of Uncertainty in Measurement (GUM) JCGM 100:2008. 1995. Available online: http://www.bipm.org/en/publications/guides (accessed on 15 July 2018).
- Hans, I.; Burgdorf, M.; John, V.O.; Mittaz, J.; Buehler, S.A. Noise performance of microwave humidity sounders over their life time. Atmos. Meas. Tech. 2017, 10, 4927–4945. [Google Scholar] [CrossRef]
- Tian, M.; Zou, X.; Weng, F. Use of Allan Deviation for Characterizing Satellite Microwave Sounder Noise Equivalent Differential Temperature (NEDT). IEEE Geosci. Remote Sens. Lett. 2015, 12, 2477–2480. [Google Scholar] [CrossRef]
- Merchant, C.J.; Woolliams, E.; Mittaz, J. Uncertainty and Error Correlation Quantification for FIDUCEO easyFCDR Products: Mathematical Recipes, v0.9; Technical Report; University of Reading, National Physical Laboratory: Reading, Berkshire, UK, 2017. [Google Scholar]
- NOAA-OSPO. POES Operational Status Webpage. 2015. Available online: http://www.ospo.noaa.gov/Operations/POES/status.html (accessed on 14 December 2017).
- Burgdorf, M.; Hans, I.; Prange, M.; Lang, T.; Buehler, S.A. Inter-channel uniformity of a microwave sounder in space. Atmos. Meas. Tech. 2018, 11. [Google Scholar] [CrossRef]
- Giering, R.; Quast, R.; Mittaz, J.; Hunt, S.; Harris, P.; Wooliams, E. Harmonisation of fundamental satellite data records. Remote Sens. 2019. in preparation. [Google Scholar]
- Burgdorf, M. Disk-Integrated Lunar Brightness Temperatures Between 89 and 190 GHz. Adv. Astron. 2019. submitted. [Google Scholar]






| Instrument and Satellite | Launched | End of Life | FCDR start date | FCDR End Date |
|---|---|---|---|---|
| SSMT-2 F11 | 28 November 1991 | 7 August 2000 | 5 July 1994 | 2 April 1995 |
| SSMT-2 F12 | 29 August 1994 | 13 October 2008 | 13 October 1994 | 8 January 2001 |
| SSMT-2 F14 | 4 April 1994 | 2015 | 28 April 1997 | 10 January 2005 |
| SSMT-2 F15 | 12 December 1999 | 2015 | 24 January 2000 | 2 January 2005 |
| AMSU-B NOAA-15 | 13 May 1998 | 28 March 2011 | 1 January 1999 | 28 March 2011 |
| AMSU-B NOAA-16 | 21 September 2000 | 9 June 2014 | 20 March 2001 | 30 April 2014 |
| AMSU-B NOAA-17 | 24 June 2002 | 10 April 2013 | 15 October 2002 | 10 April 2013 |
| MHS NOAA-18 | 20 May 2005 | ≥2018 | 30 August 2005 | 31 December 2017 |
| MHS NOAA-19 | 6 February 2009 | ≥2018 | 1 November 2009 | 31 December 2017 |
| MHS Metop-A | 19 October 2006 | ≥2018 | 1 June 2007 | 31 December 2017 |
| MHS Metop-B | 17 September 2012 | ≥2018 | 29 January 2013 | 31 December 2017 |
| Channel (in This Article) | Orig. Channel | Frequency in GHz | Total Bandwidth in GHz | Pre-Launch NET in K | |
|---|---|---|---|---|---|
| 1 | 4 | 91.655 ± 1.250 | 3 | 0.6 | |
| 2 | 5 | 150.00 ± 1.25 | 3 | 0.6 | |
| SSMT-2 | 3 | 2 | 183.31 ± 1.00 | 1 | 0.8 |
| 4 | 1 | 183.31 ± 3.00 | 2 | 0.6 | |
| 5 | 3 | 183.31 ± 7.00 | 3 | 0.6 | |
| 1 | 16 | 89.0 ± 0.9 | 2 | 0.37 | |
| 2 | 17 | 150.0 ± 0.9 | 2 | 0.84 | |
| AMSU-B | 3 | 18 | 183.31 ± 1.0 | 1 | 1.06 |
| 4 | 19 | 183.31 ± 3.0 | 2 | 0.70 | |
| 5 | 20 | 183.31 ± 7.0 | 4 | 0.60 | |
| 1 | H1 | 89.0 | 2.8 | 0.22 | |
| 2 | H2 | 157.0 | 2.8 | 0.34 | |
| MHS | 3 | H3 | 183.31 ± 1.0 | 1 | 0.51 |
| 4 | H4 | 183.31 ± 3.0 | 2 | 0.40 | |
| 5 | H5 | 190.31 | 2.2 | 0.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hans, I.; Burgdorf, M.; Buehler, S.A.; Prange, M.; Lang, T.; John, V.O. An Uncertainty Quantified Fundamental Climate Data Record for Microwave Humidity Sounders. Remote Sens. 2019, 11, 548. https://doi.org/10.3390/rs11050548
Hans I, Burgdorf M, Buehler SA, Prange M, Lang T, John VO. An Uncertainty Quantified Fundamental Climate Data Record for Microwave Humidity Sounders. Remote Sensing. 2019; 11(5):548. https://doi.org/10.3390/rs11050548
Chicago/Turabian StyleHans, Imke, Martin Burgdorf, Stefan A. Buehler, Marc Prange, Theresa Lang, and Viju O. John. 2019. "An Uncertainty Quantified Fundamental Climate Data Record for Microwave Humidity Sounders" Remote Sensing 11, no. 5: 548. https://doi.org/10.3390/rs11050548
APA StyleHans, I., Burgdorf, M., Buehler, S. A., Prange, M., Lang, T., & John, V. O. (2019). An Uncertainty Quantified Fundamental Climate Data Record for Microwave Humidity Sounders. Remote Sensing, 11(5), 548. https://doi.org/10.3390/rs11050548