Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season
Abstract
:1. Introduction
2. ZTDs and Tropospheric Gradients
2.1. Benchmark Data Set
2.2. GNSS ZTDs and Tropospheric Gradients
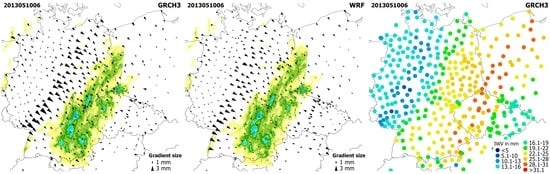
2.3. NWM ZTDs and Tropospheric Gradients
3. Method
3.1. Convert Tropospheric Gradients to Horizontal ZWD Gradients
3.2. Interpolation Algorithm
4. Results
4.1. Experiment with NWM Data
4.2. Experiment with GNSS Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. 1998, 103, 5019–5035. [Google Scholar] [CrossRef] [Green Version]
- Van Baelen, J.; Reverdy, M.; Tridon, F.; Labbouz, L.; Dick, G.; Bender, M.; Hagen, M. On the relationship between water vapour and evolution and the life cycle of precipitation systems. Q. J. R. Meteorol. Soc. 2011, 137, 204–223. [Google Scholar] [CrossRef]
- Labbouz, L.; Van Baelen, J.; Tridon, F.; Reverdy, M.; Hagen, M.; Bender, M.; Dick, G.; Gorgas, T.; Planche, C. Precipitation on the lee side of the Vosges Mountains: Multi-instrumental study of one case from the COPS campaign. Meteorol. Z. 2013, 22, 413–432. [Google Scholar] [CrossRef] [Green Version]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; et al. Review of the state of the art and future prospects of the ground-based GNSS meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zus, F.; Lu, C.; Ning, T.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Retrieving high-resolution tropospheric gradients from multiconstellation GNSS observations. Geophys. Res. Lett. 2015, 42, 4173–4181. [Google Scholar] [CrossRef] [Green Version]
- Morel, L.; Pottiaux, E.; Durand, F.; Fund, F.; Boniface, K.; de Oliveira, P.S.; Van Baelen, J. Validity and behaviour of tropospheric gradients estimated by GPS in Corsica. Adv. Space Res. 2015, 55, 135–149. [Google Scholar] [CrossRef]
- Douša, J.; Dick, G.; Kačmařík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef] [Green Version]
- Zus, F.; Deng, Z.; Wickert, J. The impact of higher-order ionospheric effects on estimated tropospheric parameters in Precise Point Positioning. Radio Sci. 2017, 52, 963–971. [Google Scholar] [CrossRef] [Green Version]
- Douša, J.; Václavovic, P.; Eliaš, M. Tropospheric products of the second European GNSS reprocessing (1996–2014). Atmos. Meas. Tech. 2017, 10, 3589–3607. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Zus, F.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Sensitivity of GNSS tropospheric gradients to processing options. Ann. Geophys. 2018. [Google Scholar] [CrossRef]
- Brenot, H.; Neméghaire, J.; Delobbe, L.; Clerbaux, N.; Meutter, P.; Deckmyn, A.; Delcloo, A.; Frappez, L.; Van Roozendael, M. Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 2013, 13, 5425–5449. [Google Scholar] [CrossRef] [Green Version]
- Douša, J.; Eliaš, M.; Václavovic, P.; Eben, K.; Krč, P. A two-stage tropospheric correction combining data from GNSS and numerical weather model. GPS Solut. 2018, 22, 77. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. 1997, 102, 20489–20502. [Google Scholar] [CrossRef] [Green Version]
- Douša, J.; Václavovic, P.; Zhao, L.; Kačmařík, M. New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks. Remote Sens. 2018, 10, 232. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Václavovic, P.; Douša, J. Backward smoothing for precise GNSS applications. Adv. Space Res. 2015, 56, 1627–1634. [Google Scholar] [CrossRef]
- Gérard, P.; Luzum, B. (Eds.) IERS Technical Note No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; p. 179. ISBN 3-89888-989-6. [Google Scholar]
- Schmid, R.; Dach, R.; Collilieux, X.; Jaeggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef]
- Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS contribution to ITRF2014. J. Geod. 2016, 90, 611–630. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 943–951. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR tech. note NCAR/TN-475+STR; NCAR: Boulder, CO, USA, 2008. [Google Scholar]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long–lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Tewri, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 12–16 January 2004; pp. 11–15. [Google Scholar]
- Jimenez, P.A.; Jimy Dudhia, J.; Gonzalez-Rouco, F.; Navarro, J.; Montavez, J.P.; Garcia-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Zus, F.; Bender, M.; Deng, Z.; Dick, G.; Heise, S.; Shang-Guan, M.; Wickert, J. A methodology to compute GPS slant total delays in a numerical weather model. Radio Sci. 2012, 47, RS2018. [Google Scholar] [CrossRef]
- Zus, F.; Dick, G.; Douša, J.; Heise, S.; Wickert, J. The rapid and precise computation of GPS slant total delays and mapping factors utilizing a numerical weather model. Radio Sci. 2014, 49, 207–216. [Google Scholar] [CrossRef] [Green Version]
- Zus, F.; Dick, G.; Heise, S.; Wickert, J. A forward operator and its adjoint for GPS slant total delays. Radio Sci. 2015, 50, 393–405. [Google Scholar] [CrossRef] [Green Version]
- Copernicus Climate Change Service (C3S) (2017): ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS), date of access. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 1 February 2019).
- Elosegui, P.; Davis, J.L.; Gradinarsky, L.P.; Elgered, G.; Johansson, J.M.; Tahmoush, D.A.; Rius, A. Sensing atmospheric structure using small-scale space geodetic networks. Geophys. Res. Lett. 1999, 26, 2445–2448. [Google Scholar] [CrossRef] [Green Version]
- Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Dick, G.; Wickert, J. Estimating the Impact of Global Navigation Satellite System Horizontal Delay Gradients in Variational Data Assimilation. Remote Sens. 2019, 11, 41. [Google Scholar] [CrossRef]
- Douša, J.; Eliaš, M. An improved model for calculating tropospheric wet delay. Geophys. Res. Lett. 2014, 41, 4389–4397. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Xu, C.; Li, Y.; Gao, Y. Impacts of real-time satellite clock errors on GPS precise point positioning-based troposphere zenith delay estimation. J. Geod. 2015, 89, 747. [Google Scholar] [CrossRef]










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sens. 2019, 11, 674. https://doi.org/10.3390/rs11060674
Zus F, Douša J, Kačmařík M, Václavovic P, Balidakis K, Dick G, Wickert J. Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sensing. 2019; 11(6):674. https://doi.org/10.3390/rs11060674
Chicago/Turabian StyleZus, Florian, Jan Douša, Michal Kačmařík, Pavel Václavovic, Kyriakos Balidakis, Galina Dick, and Jens Wickert. 2019. "Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season" Remote Sensing 11, no. 6: 674. https://doi.org/10.3390/rs11060674
APA StyleZus, F., Douša, J., Kačmařík, M., Václavovic, P., Balidakis, K., Dick, G., & Wickert, J. (2019). Improving GNSS Zenith Wet Delay Interpolation by Utilizing Tropospheric Gradients: Experiments with a Dense Station Network in Central Europe in the Warm Season. Remote Sensing, 11(6), 674. https://doi.org/10.3390/rs11060674