Chimera: A Multi-Task Recurrent Convolutional Neural Network for Forest Classification and Structural Estimation
Abstract
:1. Introduction
Objectives
2. Materials and Methods
2.1. Region of Analysis
2.2. Predictor Variables—Optical Data
2.2.1. NAIP (National Agricultural Imagery Program)
2.2.2. Landsat 7
2.3. Predictor Variables—Ancillary Data
2.3.1. PRISM (Parameter-Elevation Regressions on Independent Slopes Model)
2.3.2. USGS NED (National Elevation Dataset)
2.4. Response Variables
Training Data Targets: FIA Sampling and Database Parameter Usage
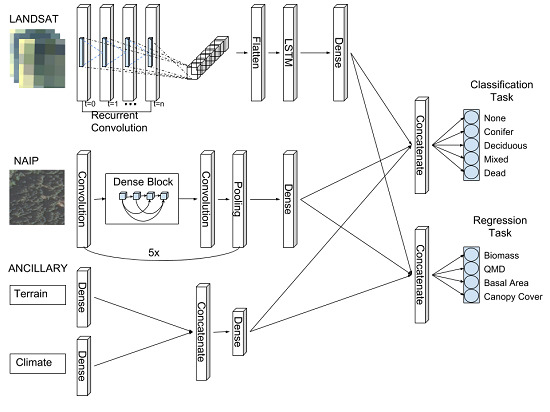
2.5. Chimera RCNN Architecture
2.6. Chimera Comparisons with RF and SVM
2.7. Model Ensembling
3. Results
3.1. Model Diagnostics and Input Experiments
3.1.1. Classification Task Diagnostics
3.1.2. Regression Task Diagnostics
3.2. Model Comparison Experiment
4. Discussion
Caveats Associated with the Training Data
5. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Above ground biomass |
| ANC | Ancillary climate and terrain data |
| BIM | Best individual chimera model |
| CA | California |
| CE | Chimera ensemble |
| CNN | Convolutional neural network |
| DEM | Digital elevation model |
| GEDI | Global Ecosystem Dynamics Investigation LiDAR |
| GEE | Google Earth Engine |
| GLAS | Geoscience laser altimeter system |
| GLCM | Gray level co-occurrence matrix |
| FIA | Forest inventory and analysis |
| LS | Landsat |
| LSTM | Long-short term memory cell |
| MODIS | Moderate resolution imaging spectroradiometer |
| MTL | Multi-task learning |
| NASA | National Aeronautics and Space Administration |
| NISAR | NASA-ISRO Synthetic Aperture Radar |
| NAIP | National Agriculture Inventory Program |
| NED | National elevation dataset |
| NV | Nevada |
| PRISM | Parameter-elevation regressions on independent slopes model |
| QA | Quality assessment |
| QMD | Quadratic mean diameter |
| RCNN | Recurrent convolutional neural network |
| ReLU | Rectified linear units |
| RF | Random forest |
| RGB | Red-green-blue |
| RMSE | Root mean squared error |
| SD | Standard deviation |
| SDGL | Standard deviation of gray levels |
| SVM | Support vector machine |
| TOA | Top Of atmosphere |
| USDA | United States Department of Agriculture |
| USGS | United States Geological Survey |
| YOLO | You only look once |
Appendix A. Additional Figures










References
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Chen, Q. Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS J. Photogramm. Remote Sens. 2015, 106, 95–106. [Google Scholar] [CrossRef]
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and earlier spring increase western US forest wildfire activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef]
- Cook, J.H.; Beyea, J.; Keeler, K.H. Potential impacts of biomass production in the United States on biological diversity. Annu. Rev. Energy Environ. 1991, 16, 401–431. [Google Scholar] [CrossRef]
- Malmsheimer, R.W.; Bowyer, J.L.; Fried, J.S.; Gee, E.; Izlar, R.; Miner, R.A.; Munn, I.A.; Oneil, E.; Stewart, W.C. Managing forests because carbon matters: Integrating energy, products, and land management policy. J. For. 2011, 109, S7–S50. [Google Scholar]
- Zolkos, S.; Goetz, S.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Wilson, B.T.; Woodall, C.W.; Griffith, D.M. Imputing forest carbon stock estimates from inventory plots to a nationally continuous coverage. Carbon Balance Manag. 2013, 8, 1. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.; Tyukavina, A.; Thau, D.; Stehman, S.; Goetz, S.; Loveland, T.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.; Clark, D.B.; Hofton, M.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using lidar remote sensing at La Selva, Costa Rica. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Blackard, J.; Finco, M.; Helmer, E.; Holden, G.; Hoppus, M.; Jacobs, D.; Lister, A.; Moisen, G.; Nelson, M.; Riemann, R.; et al. Mapping US forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. A review of remote sensing of forest biomass and biofuel: Options for small-area applications. GISci. Remote Sens. 2011, 48, 141–170. [Google Scholar] [CrossRef]
- Asner, G.P.; Hughes, R.F.; Mascaro, J.; Uowolo, A.L.; Knapp, D.E.; Jacobson, J.; Kennedy-Bowdoin, T.; Clark, J.K. High-resolution carbon mapping on the million-hectare Island of Hawaii. Front. Ecol. Environ. 2011, 9, 434–439. [Google Scholar] [CrossRef]
- Woodcock, C.E.; Allen, R.; Anderson, M.; Belward, A.; Bindschadler, R.; Cohen, W.; Gao, F.; Goward, S.N.; Helder, D.; Helmer, E.; et al. Free access to Landsat imagery. Science 2008, 320, 1011. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Smith, W.K.; Jones, M.O.; Moreno, A.; Erickson, T.A.; Naugle, D.E.; Running, S.W. Terrestrial primary production for the conterminous United States derived from Landsat 30 m and MODIS 250 m. Remote Sens. Ecol. Conserv. 2018. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground forest biomass estimation with Landsat and LiDAR data and uncertainty analysis of the estimates. Int. J. For. Res. 2012, 2012, 436537. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture Farm Service Agency. National Agriculture Imagery Program. 2016. Available online: https://www.fsa.usda.gov/programs-and-services/aerial-photography/imageryprograms/naip-imagery/index (accessed on 12 September 2018).
- Hogland, J.S.; Anderson, N.M.; Chung, W.; Wells, L. Estimating forest characteristics using NAIP imagery and ArcObjects. In Proceedings of the 2014 ESRI Users Conference, San Diego, CA, USA, 14–18 July 2014; Environmental Systems Research Institute: Redlands, CA, USA, 2014; pp. 155–181. [Google Scholar]
- Hulet, A.; Roundy, B.A.; Petersen, S.L.; Bunting, S.C.; Jensen, R.R.; Roundy, D.B. Utilizing national agriculture imagery program data to estimate tree cover and biomass of pinon and juniper woodlands. Rangel. Ecol. Manag. 2014, 67, 563–572. [Google Scholar] [CrossRef]
- Interdonato, R.; Ienco, D.; Gaetano, R.; Ose, K. DuPLO: A DUal view Point deep Learning architecture for time series classificatiOn. ISPRS J. Photogramm. Remote Sens. 2019, 149, 91–104. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.; Townshend, J. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Gopal, S.; Woodcock, C. Remote sensing of forest change using artificial neural networks. IEEE Trans. Geosci. Remote Sens. 1996, 34, 398–404. [Google Scholar] [CrossRef]
- Minetto, R.; Segundo, M.P.; Sarkar, S. Hydra: An Ensemble of Convolutional Neural Networks for Geospatial Land Classification. arXiv, 2018; arXiv:1802.03518. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN features off-the-shelf: An astounding baseline for recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Columbus, OH, USA, 23–28 June 2014; pp. 806–813. [Google Scholar]
- Anwer, R.M.; Khan, F.S.; van de Weijer, J.; Molinier, M.; Laaksonen, J. Binary patterns encoded convolutional neural networks for texture recognition and remote sensing scene classification. ISPRS J. Photogramm. Remote Sens. 2018, 138, 74–85. [Google Scholar] [CrossRef]
- Hogland, J.; Anderson, N.; St Peter, J.; Drake, J.; Medley, P. Mapping Forest Characteristics at Fine Resolution across Large Landscapes of the Southeastern United States Using NAIP Imagery and FIA Field Plot Data. ISPRS Int. J. Geo-Inf. 2018, 7, 140. [Google Scholar] [CrossRef]
- Ozdemir, I.; Karnieli, A. Predicting forest structural parameters using the image texture derived from WorldView-2 multispectral imagery in a dryland forest, Israel. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 701–710. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; Springer: Berlin, Germany, 2012; pp. 1097–1105. [Google Scholar]
- Liang, M.; Hu, X. Recurrent convolutional neural network for object recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3367–3375. [Google Scholar]
- Pinheiro, P.H.; Collobert, R. Recurrent convolutional neural networks for scene labeling. In Proceedings of the 31st International Conference on Machine Learning (ICML), Beijing, China, 21–26 June 2014. [Google Scholar]
- Saikat, B.; DiBiano, R.; Karki, M.; Mukhopadhyay, S.; Ganguly, S.; Nemani, R.R. DeepSat—A Learning framework for Satellite Imagery. 2016. Available online: https://csc.lsu.edu/~saikat/deepsat/ (accessed on 12 September 2018).
- Yang, Y.; Newsam, S. Bag-Of-Visual words and Spatial Extensions for Land-Use Classification. In Proceedings of the ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010. [Google Scholar]
- Mnih, V.; Hinton, G.E. Learning to detect roads in high-resolution aerial images. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 210–223. [Google Scholar]
- Caruana, R. A dozen tricks with multitask learning. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 165–191. [Google Scholar]
- Ruder, S. An overview of multi-task learning in deep neural networks. arXiv, 2017; arXiv:1706.05098. [Google Scholar]
- Van der Laan, M.J.; Polley, E.C.; Hubbard, A.E. Super learner. Stat. Appl. Genet. Mol. Biol. 2007, 6. [Google Scholar] [CrossRef]
- Bytnerowicz, A.; Fenn, M.E. Nitrogen deposition in California forests: A review. Environ. Pollut. 1996, 92, 127–146. [Google Scholar] [CrossRef]
- United State Department of Agriculture Forest Service. Humboldt-Toiyabe National Forest. 2018. Available online: https://www.fs.usda.gov/htnf/ (accessed on 13 September 2018).
- Google. Google Earth Engine. 2016. Available online: https://earthengine.google.com/ (accessed on 7 September 2018).
- Schrader-Patton, C.; Liknes, G.; Gatziolis, D.; Wing, B.; Nelson, M.; Miles, P.; Bixby, J.; Wendt, D.; Kepler, D.; Schaaf, A. Refining Fia Plot Locations Using lidar point clouds. In Proceedings of the Forest Inventory and Analysis (FIA) Symposium 2015, Portland, OR, USA, 8–10 December 2016. [Google Scholar]
- United States Geological Survey. Landsat Surface Reflectance Level-2 Science Products. 2018. Available online: https://www.usgs.gov/land-resources/nli/landsat/landsat-surface-reflectance?qtscience_support_page_related_con=0#qt-science_support_page_related_con (accessed on 18 September 2018).
- Kane, V.R.; Lutz, J.A.; Cansler, C.A.; Povak, N.A.; Churchill, D.J.; Smith, D.F.; Kane, J.T.; North, M.P. Water balance and topography predict fire and forest structure patterns. For. Ecol. Manag. 2015, 338, 1–13. [Google Scholar] [CrossRef]
- Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
- Daly, C.; Gibson, W.P.; Taylor, G.H.; Johnson, G.L.; Pasteris, P. A knowledge-based approach to the statistical mapping of climate. Clim. Res. 2002, 22, 99–113. [Google Scholar] [CrossRef]
- Gesch, D.; Evans, G.; Mauck, J.; Hutchinson, J.; Carswell, W.J., Jr. The National Map—Elevation. US Geol. Surv. Fact Sheet 2009, 3053, 4. Available online: https://www.univie.ac.at/cartography/lehre/thgk/doc/fs10602.pdf (accessed on 18 September 2018).
- Gesch, D.B.; Oimoen, M.J.; Evans, G.A. Accuracy Assessment of the US Geological Survey National Elevation Dataset, and Comparison With Other Large-Area Elevation Datasets: SRTM and ASTER; Technical Report; US Geological Survey: Reston, VA, USA, 2014.
- Gemmell, F. Effects of forest cover, terrain, and scale on timber volume estimation with Thematic Mapper data in a Rocky Mountain site. Remote Sens. Environ. 1995, 51, 291–305. [Google Scholar] [CrossRef]
- Parker, A.J. Stand structure in subalpine forests of Yosemite National Park, California. For. Sci. 1988, 34, 1047–1058. [Google Scholar]
- White, D.; Kimerling, J.A.; Overton, S.W. Cartographic and geometric components of a global sampling design for environmental monitoring. Cartogr. Geogr. Inf. Syst. 1992, 19, 5–22. [Google Scholar] [CrossRef]
- Coulston, J.W.; Moisen, G.G.; Wilson, B.T.; Finco, M.V.; Cohen, W.B.; Brewer, C.K. Modeling percent tree canopy cover: A pilot study. Photogramm. Eng. Remote Sens. 2012, 78, 715–727. [Google Scholar] [CrossRef]
- Burrill, E.A.; Wilson, A.M.; Turner, J.A.; Pugh, S.A.; Menlove, J.; Christiansen, G.; Conkling, B.L.; David, W. The Forest Inventory and Analysis Database: Database Description And User Guide Version 7.2 for Phase 2; Technical Report; U.S. Department of Agriculture, Forest Service: Reston, VA, USA, 2017.
- Toney, C.; Shaw, J.D.; Nelson, M.D. A stem-map model for predicting tree canopy cover of Forest Inventory and Analysis (FIA) plots. In Proceedings of the Forest Inventory and Analysis (FIA) Symposium 2008, Park City, UT, USA, 21–23 October 2008; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2009; Volume 56. [Google Scholar]
- Chollet, F. Keras: Deep Learning Library for Theano and Tensorflow. 2015, Volume 7. Available online: https://keras.io (accessed on 18 September 2018).
- Trottier, L.; Giguère, P.; Chaib-draa, B. Multi-Task Learning by Deep Collaboration and Application in Facial Landmark Detection. arXiv, 2017; arXiv:1711.00111. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; van der Maaten, L. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Volume 1, p. 3. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Donahue, J.; Anne Hendricks, L.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Saenko, K.; Darrell, T. Long-term recurrent convolutional networks for visual recognition and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2625–2634. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Young, S.; Abdou, T.; Bener, A. Deep Super Learner: A Deep Ensemble for Classification Problems. In Proceedings of the Advances in Artificial Intelligence: 31st Canadian Conference on Artificial Intelligence, Toronto, ON, Canada, 8–11 May 2018; pp. 84–95. [Google Scholar]
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst; Esri: Redlands, CA, USA, 2001; Volume 380. [Google Scholar]
- Cressie, N.; Ver Hoef, J. Spatial Statistical Analysis of Environmental and Ecological Data; Iowa State University, Department of Statistics, Statistical Laboratory: Ames, IA, USA, 1991. [Google Scholar]
- Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ. 2002, 79, 305–319. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; López-Sánchez, C.A.; Álvarez-González, J.G.; García-Gutiérrez, J. A comparison of machine learning techniques applied to landsat-5 TM spectral data for biomass estimation. Can. J. Remote Sens. 2016, 42, 690–705. [Google Scholar] [CrossRef]
- Wilson, B.T.; Lister, A.J.; Riemann, R.I. A nearest-neighbor imputation approach to mapping tree species over large areas using forest inventory plots and moderate resolution raster data. For. Ecol. Manag. 2012, 271, 182–198. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J. Predictive mapping of forest composition and structure with direct gradient analysis and nearest-neighbor imputation in coastal Oregon, USA. Can. J. For. Res. 2002, 32, 725–741. [Google Scholar] [CrossRef]
- Franco-Lopez, H.; Ek, A.R.; Robinson, A.P. A review of methods for updating forest monitoring system estimates. In Integrated Tools for Natural Resources Inventories in the 21st Century; Hansen, M., Burk, T., Eds.; Gen. Tech. Rep. NC-212; U.S. Dept. of Agriculture, Forest Service, North Central Forest Experiment Station: St. Paul, MN, USA, 2000; Volume 212, pp. 494–500. [Google Scholar]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Hampton, H.M.; Sesnie, S.E.; Bailey, J.D.; Snider, G.B. Estimating regional wood supply based on stakeholder consensus for forest restoration in northern Arizona. J. For. 2011, 109, 15–26. [Google Scholar]
- Zhu, X.; Liu, D. Improving forest aboveground biomass estimation using seasonal Landsat NDVI time-series. ISPRS J. Photogramm. Remote Sens. 2015, 102, 222–231. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Battles, J.J.; Saah, D. Integration of airborne lidar and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
- Franklin, S.; Hall, R.; Moskal, L.; Maudie, A.; Lavigne, M. Incorporating texture into classification of forest species composition from airborne multispectral images. Int. J. Remote Sens. 2000, 21, 61–79. [Google Scholar] [CrossRef]
- Coburn, C.; Roberts, A. A multiscale texture analysis procedure for improved forest stand classification. Int. J. Remote Sens. 2004, 25, 4287–4308. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- Dubayah, R.; Goetz, S.; Blair, J.; Fatoyinbo, T.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The global ecosystem dynamics investigation. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar]
- Alvarez-Salazar, O.; Hatch, S.; Rocca, J.; Rosen, P.; Shaffer, S.; Shen, Y.; Sweetser, T.; Xaypraseuth, P. Mission design for NISAR repeat-pass Interferometric SAR. Sens. Syst. Next-Gener. Satellites XVIII Int. Soc. Opt. Photonics 2014, 9241, 92410C. [Google Scholar]
- Dickson, B.G.; Sisk, T.D.; Sesnie, S.E.; Reynolds, R.T.; Rosenstock, S.S.; Vojta, C.D.; Ingraldi, M.F.; Rundall, J.M. Integrating single-species management and landscape conservation using regional habitat occurrence models: The northern goshawk in the Southwest, USA. Landsc. Ecol. 2014, 29, 803–815. [Google Scholar] [CrossRef]
- Finney, M.A. An overview of FlamMap fire modeling capabilities. In Proceedings of the Fuels Management-How to Measure Success: Conference Proceedings, Portland, OR, USA, 28–30 March 2006; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; Volume 41, pp. 213–220. [Google Scholar]
- Gray, M.E.; Zachmann, L.J.; Dickson, B.G. A weekly, near real-time dataset of the probability of large wildfire across western US forests and woodlands. Earth Syst. Sci. Data Discuss 2018, 10, 1715–1727. [Google Scholar] [CrossRef]









| Class | Training/Validation | Testing | ||
|---|---|---|---|---|
| (%) | (%) | |||
| None | 6226 | 0.66 | 330 | 0.66 |
| Conifer | 1686 | 0.18 | 92 | 0.18 |
| Deciduous | 407 | 0.04 | 15 | 0.03 |
| Mixed | 1105 | 0.12 | 62 | 0.12 |
| Dead | 43 | 1 | ||
| Metric | Training/Validation | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Min | Median | Max | Mean | SD | Min | Median | Max | |
| AGB (Mg/ha) | 99.62 | 139.04 | 0.1 | 41.0 | 3240.2 | 103.39 | 134.48 | 0.1 | 40.8 | 907.4 |
| QMD (in) | 15.15 | 7.20 | 1.0 | 13.2 | 87.2 | 15.61 | 7.49 | 5.0 | 13.4 | 42.1 |
| Basal Area (ft/ac) | 107.69 | 88.14 | 0.6 | 88.1 | 1201.6 | 107.84 | 85.48 | 1.1 | 86.6 | 435.2 |
| Canopy Cover (%) | 40.56 | 25.76 | 0.5 | 35.0 | 99.0 | 40.21 | 24.71 | 3.0 | 35.1 | 99.0 |
| Classification Metric (F1-Score) | ANC | NAIP | NAIP + ANC | LS | LS + ANC | NAIP + LS | FULL |
| None | 0.83 | 0.99 | 0.99 | 0.97 | 0.97 | 0.99 | 0.98 |
| Conifer | 0.57 | 0.80 | 0.82 | 0.78 | 0.81 | 0.85 | 0.81 |
| Deciduous | 0.00 | 0.46 | 0.39 | 0.27 | 0.39 | 0.65 | 0.60 |
| Mixed | 0.27 | 0.59 | 0.61 | 0.56 | 0.63 | 0.74 | 0.66 |
| Dead | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Overall | 0.68 | 0.89 | 0.89 | 0.86 | 0.88 | 0.92 | 0.90 |
| Regression Metric () | ANC | NAIP | NAIP + ANC | LS | LS + ANC | NAIP + LS | FULL |
| AGB | 0.00 | 0.70 | 0.70 | 0.74 | 0.73 | 0.75 | 0.78 |
| QMD | 0.12 | 0.78 | 0.76 | 0.68 | 0.67 | 0.78 | 0.79 |
| Basal Area | 0.04 | 0.75 | 0.76 | 0.78 | 0.79 | 0.78 | 0.81 |
| Canopy Cover | 0.07 | 0.82 | 0.82 | 0.83 | 0.83 | 0.84 | 0.85 |
| Overall (mean ) | 0.06 | 0.76 | 0.76 | 0.76 | 0.75 | 0.78 | 0.81 |
| Regression Metric (RMSE) | ANC | NAIP | NAIP + ANC | LS | LS + ANC | NAIP + LS | FULL |
| AGB (Mg/ha) | 92.62 | 50.67 | 50.45 | 46.95 | 48.05 | 46.45 | 43.34 |
| QMD (in) | 8.07 | 3.99 | 4.24 | 4.87 | 4.90 | 4.04 | 3.90 |
| Basal Area (ft/ac) | 69.90 | 35.86 | 34.65 | 33.16 | 32.72 | 33.42 | 30.91 |
| Canopy Cover (%) | 23.05 | 10.04 | 9.99 | 9.85 | 9.99 | 9.47 | 9.25 |
| Class | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|
| CE BIM SVM RF | CE BIM SVM RF | CE BIM SVM RF | ||
| None | 0.99 0.98 0.96 0.97 | 0.99 0.99 0.97 0.99 | 0.99 0.99 0.96 0.98 | 330 |
| Conifer | 0.81 0.82 0.73 0.79 | 0.91 0.90 0.76 0.87 | 0.86 0.86 0.74 0.83 | 92 |
| Deciduous | 0.60 0.54 0.36 0.54 | 0.60 0.47 0.33 0.40 | 0.60 0.50 0.34 0.46 | 15 |
| Mixed | 0.81 0.81 0.63 0.78 | 0.68 0.68 0.58 0.65 | 0.74 0.74 0.61 0.71 | 62 |
| Dead | 0.00 0.00 0.00 0.00 | 0.00 0.00 0.00 0.00 | 0.00 0.00 0.00 0.00 | 1 |
| Metric () | CE | BIM | RF | SVM |
| AGB | 0.84 | 0.83 | 0.76 | 0.68 |
| QMD | 0.81 | 0.80 | 0.76 | 0.69 |
| Basal Area | 0.87 | 0.85 | 0.78 | 0.79 |
| Canopy Cover | 0.89 | 0.88 | 0.84 | 0.84 |
| Metric () | CE | BIM | RF | SVM |
| AGB (Mg/ha) | 37.28 | 38.19 | 45.71 | 52.11 |
| QMD (in) | 3.74 | 3.86 | 4.19 | 4.81 |
| Basal Area (ft/ac) | 25.88 | 27.43 | 33.16 | 32.73 |
| Canopy Cover (%) | 8.01 | 8.10 | 9.64 | 9.68 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, T.; Rasmussen, B.P.; Dickson, B.G.; Zachmann, L.J. Chimera: A Multi-Task Recurrent Convolutional Neural Network for Forest Classification and Structural Estimation. Remote Sens. 2019, 11, 768. https://doi.org/10.3390/rs11070768
Chang T, Rasmussen BP, Dickson BG, Zachmann LJ. Chimera: A Multi-Task Recurrent Convolutional Neural Network for Forest Classification and Structural Estimation. Remote Sensing. 2019; 11(7):768. https://doi.org/10.3390/rs11070768
Chicago/Turabian StyleChang, Tony, Brandon P. Rasmussen, Brett G. Dickson, and Luke J. Zachmann. 2019. "Chimera: A Multi-Task Recurrent Convolutional Neural Network for Forest Classification and Structural Estimation" Remote Sensing 11, no. 7: 768. https://doi.org/10.3390/rs11070768
APA StyleChang, T., Rasmussen, B. P., Dickson, B. G., & Zachmann, L. J. (2019). Chimera: A Multi-Task Recurrent Convolutional Neural Network for Forest Classification and Structural Estimation. Remote Sensing, 11(7), 768. https://doi.org/10.3390/rs11070768