Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images
Abstract
:1. Introduction
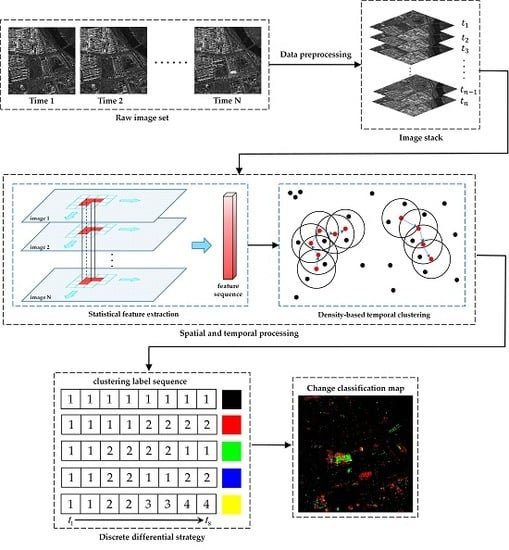
2. Materials and Methods
2.1. Time-Series SAR Data Preprocessing
2.2. Spatial Statistical Feature Extraction
2.3. Temporal Grouping Using a Density-Based Clustering Method
- Core point: for any sample , it is regarded as a core point if at least minPts are included in the circle area centered on with a radius of .
- Directly density-reachable: is directly density-reachable from if is within the distance of core point . Note that it does not satisfy the symmetry unless is also a core point.
- Density-reachable: is density-reachable from if there is a sample sequence with , and is directly density-reachable from , where all samples in the sequence are the core points, or in other words, the density-reachable meets the transitivity.
- Outliers: is an outlier or a noise point if it is not density-reachable from any other sample in .
| Algorithm 1. Temporal clustering for the pixel sequence (DBSCAN). |
| Input: temporal features of the patch sequence and the neighborhood parameters . |
| Output: the clustering labels for the pixel sequence. |
| 1: Mark all samples in dataset as unvisited, initialize the cluster index ; |
| 2: for each sample in dataset do 3: if has been classified as a cluster or marked as noise then 4: continue; 5: else 6: if the samples contained in neighborhood of () is less than minPts then 7: Mark as a outlier or noise point; 8: else 9: Mark as a core point, create a new cluster and add all points in to , 10: and assign the cluster index of as ; |
| 11: for each point () unvisited in do 12: Add the point in unclassified into any other cluster to if contains at least minPts points; 13: Assign the cluster index of as ; |
| 14: end for 15: end if 16: end if |
| 17: end for |
2.4. Classification with a Discrete Differential Strategy
2.5. Quantitative Evaluation Criteria
3. Experiments and Results
3.1. Study Site and Dataset Description
3.2. Experimental Setup and Paramter Setting
3.3. Experimental Results and Analysis
3.3.1. Test on Synthetic Time-Series SAR Images
3.3.2. Test on Realistic Time-Series SAR Images
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Malila, W.A. Change vector analysis: An approach for detecting forest changes with Landsat. In Proceedings of the LARS symposia, West Lafayette, IN, USA, 3–6 June 1980; p. 385. [Google Scholar]
- Singh, A. Review article digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- El-Kawy, O.A.; Rød, J.; Ismail, H.; Suliman, A. Land use and land cover change detection in the western Nile delta of Egypt using remote sensing data. Appl. Geogr. 2011, 31, 483–494. [Google Scholar] [CrossRef]
- Chen, X.; Chen, J.; Shi, Y.; Yamaguchi, Y. An automated approach for updating land cover maps based on integrated change detection and classification methods. ISPRS J. Photogramm. Remote Sens. 2012, 71, 86–95. [Google Scholar] [CrossRef]
- Gamba, P.; Dell’Acqua, F.; Lisini, G. Change detection of multitemporal SAR data in urban areas combining feature-based and pixel-based techniques. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2820–2827. [Google Scholar] [CrossRef]
- Ban, Y.; Yousif, O.A. Multitemporal spaceborne SAR data for urban change detection in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1087–1094. [Google Scholar] [CrossRef]
- Stramondo, S.; Bignami, C.; Chini, M.; Pierdicca, N.; Tertulliani, A. Satellite radar and optical remote sensing for earthquake damage detection: Results from different case studies. Int. J. Remote Sens. 2006, 27, 4433–4447. [Google Scholar] [CrossRef]
- Tewkesbury, A.P.; Comber, A.J.; Tate, N.J.; Lamb, A.; Fisher, P.F. A critical synthesis of remotely sensed optical image change detection techniques. Remote Sens. Environ. 2015, 160, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef] [Green Version]
- Moser, G.; Serpico, S.B. Generalized minimum-error thresholding for unsupervised change detection from SAR amplitude imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef] [Green Version]
- Gong, M.; Zhou, Z.; Ma, J. Change detection in synthetic aperture radar images based on image fusion and fuzzy clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef] [PubMed]
- Gong, M.; Zhao, J.; Liu, J.; Miao, Q.; Jiao, L. Change detection in synthetic aperture radar images based on deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 125–138. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR processing and products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Sun, J.; Yu, W.; Deng, Y. The SAR payload design and performance for the GF-3 mission. Sensors 2017, 17, 2419. [Google Scholar] [CrossRef]
- Coppin, P.; Lambin, E.; Jonckheere, I.; Muys, B. Digital change detection methods in natural ecosystem monitoring: A review. In Analysis of Multi-Temporal Remote Sensing Images; World Scientific: Singapore, 2002; pp. 3–36. [Google Scholar]
- Radke, R.J.; Andra, S.; Al-Kofahi, O.; Roysam, B. Image change detection algorithms: A systematic survey. IEEE Trans. Image Process. 2005, 14, 294–307. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Conradsen, K.; Nielsen, A.A.; Skriver, H. Determining the points of change in time series of polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3007–3024. [Google Scholar] [CrossRef]
- Dogan, O.; Perissin, D. Detection of Multitransition Abrupt Changes in Multitemporal SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3239–3247. [Google Scholar] [CrossRef]
- Muro, J.; Canty, M.; Conradsen, K.; Hüttich, C.; Nielsen, A.A.; Skriver, H.; Remy, F.; Strauch, A.; Thonfeld, F.; Menz, G. Short-Term Change Detection in Wetlands Using Sentinel-1 Time Series. Remote Sens. 2016, 8, 795. [Google Scholar] [CrossRef]
- Liu, W.; Yang, J.; Zhao, J.; Shi, H.; Yang, L. An unsupervised change detection method using time-series of PolSAR images from radarsat-2 and gaofen-3. Sensors 2018, 18, 559. [Google Scholar]
- Atto, A.M.; Trouvé, E.; Berthoumieu, Y.; Mercier, G. Multidate divergence matrices for the analysis of SAR image time series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1922–1938. [Google Scholar] [CrossRef]
- Le, T.T.; Atto, A.M.; Trouve, E. Change analysis using multitemporal Sentinel-1 SAR images. In Proceedings of the Geoscience & Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Su, X.; Deledalle, C.-A.; Tupin, F.; Sun, H. NORCAMA: Change analysis in SAR time series by likelihood ratio change matrix clustering. ISPRS J. Photogramm. Remote Sens. 2015, 101, 247–261. [Google Scholar] [CrossRef] [Green Version]
- Bujor, F.; Trouvé, E.; Valet, L.; Nicolas, J.M.; Rudant, J.P. Application of log-cumulants to the detection of spatiotemporal discontinuities in multitemporal SAR images. Geosci. Remote Sens. IEEE Trans. 2004, 42, 2073–2084. [Google Scholar] [CrossRef]
- Quin, G.; Pinel-Puyssegur, B.; Nicolas, J.-M.; Loreaux, P. MIMOSA: An automatic change detection method for SAR time series. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5349–5363. [Google Scholar] [CrossRef]
- Freeman, A. SAR calibration: An overview. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1107–1121. [Google Scholar] [CrossRef]
- Townshend, J.R.; Justice, C.O.; Gurney, C.; McManus, J. The impact of misregistration on change detection. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1054–1060. [Google Scholar] [CrossRef] [Green Version]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and interferometric processing software. In Proceedings of the Ers-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2000; p. 1620. [Google Scholar]
- Chierchia, G.; Gheche, M.E.; Scarpa, G.; Verdoliva, L. Multitemporal SAR Image Despeckling Based on Block-Matching and Collaborative Filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5467–5480. [Google Scholar] [CrossRef]
- Lv, X.; Yazıcı, B.; Zeghal, M.; Bennett, V.; Abdoun, T. Joint-Scatterer Processing for Time-Series InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7205–7221. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Kdd, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Yang, Y. An evaluation of statistical approaches to text categorization. Inf. Retr. 1999, 1, 69–90. [Google Scholar] [CrossRef]
- Yuan, J.; Lv, X.; Li, R. A Speckle Filtering Method Based on Hypothesis Testing for Time-Series SAR Images. Remote Sens. 2018, 10, 1383. [Google Scholar] [CrossRef]
- Sander, J.; Ester, M.; Kriegel, H.-P.; Xu, X. Density-based clustering in spatial databases: The algorithm gdbscan and its applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. (Tods) 2017, 42, 19. [Google Scholar] [CrossRef]











| Change Types | Number of Clusters | Category Sequence Example |
|---|---|---|
| Unchanged | 1 | {1,1,…} |
| Step change | 2 | {1,1,…,2,2,…} |
| Impulse change | 2 | {1,1,…,2,2,…,1,1,…} |
| Cycle change | 2 | {1,1,…,2,2,…,1,1,…,2,2,…} |
| Complex change | {1,1,…,2,2,…,3,3,…,4,4,…} |
| Change Areas | Step Change (Red) | Cycle Change (Blue) | Impulse Change (Green) | Complex Change (Yellow) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Length | 20 | 23 | 16 | 19 | 17 | 17 | 18 | 19 | 20 | 21 |
| Width | 20 | 23 | 18 | 25 | 16 | 23 | 20 | 22 | 17 | 18 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 988761 | 2202 | 3753 | 1236 | 197 |
| Step | 0 | 1214 | 0 | 0 | 3 |
| Impluse | 36 | 0 | 742 | 0 | 0 |
| Cycle | 3 | 0 | 2 | 1133 | 0 |
| Complex | 0 | 138 | 0 | 0 | 580 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 994725 | 423 | 358 | 441 | 202 |
| Step | 10 | 1179 | 0 | 1 | 27 |
| Impluse | 159 | 1 | 581 | 21 | 16 |
| Cycle | 9 | 0 | 5 | 1123 | 1 |
| Complex | 0 | 251 | 24 | 31 | 412 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 994916 | 442 | 509 | 268 | 14 |
| Step | 9 | 1181 | 1 | 3 | 23 |
| Impluse | 12 | 0 | 766 | 0 | 0 |
| Cycle | 7 | 0 | 0 | 1128 | 3 |
| Complex | 17 | 65 | 32 | 2 | 602 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 995604 | 189 | 154 | 202 | 0 |
| Step | 1 | 1216 | 0 | 0 | 0 |
| Impluse | 15 | 0 | 763 | 0 | 0 |
| Cycle | 2 | 0 | 0 | 1136 | 0 |
| Complex | 6 | 87 | 6 | 0 | 619 |
| Indices (%) | NORCAMA | KLD | KS2 | Proposed |
|---|---|---|---|---|
| Unchanged | ||||
| precision | 99.99 | 99.98 | 99.99 | 99.99 |
| recall | 99.26 | 99.86 | 99.88 | 99.95 |
| F1-score | 99.63 | 99.92 | 99.94 | 99.97 |
| Step change | ||||
| precision | 34.16 | 63.59 | 69.96 | 81.50 |
| recall | 99.75 | 96.88 | 97.04 | 99.92 |
| F1-score | 50.89 | 76.78 | 81.31 | 89.77 |
| Impulse change | ||||
| precision | 16.50 | 60.94 | 58.56 | 82.67 |
| recall | 95.37 | 74.81 | 98.46 | 98.07 |
| F1-score | 28.13 | 67.17 | 73.44 | 89.71 |
| Cycle change | ||||
| precision | 47.83 | 68.86 | 80.51 | 84.90 |
| recall | 99.56 | 98.51 | 99.12 | 99.82 |
| F1-score | 64.61 | 81.06 | 88.85 | 91.76 |
| Complex change | ||||
| precision | 74..36 | 62.73 | 93.77 | 100.00 |
| recall | 80.78 | 57.66 | 83.84 | 86.21 |
| F1-score | 77.44 | 60.09 | 88.53 | 92.60 |
| Macro F1-score | 64.14 | 77.00 | 86.41 | 92.76 |
| Micro F1-score | 99.24 | 99.80 | 99.86 | 99.93 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 947020 | 9467 | 6609 | 1521 | 64 |
| Step | 3883 | 18861 | 145 | 133 | 212 |
| Impluse | 2074 | 130 | 7402 | 19 | 202 |
| Cycle | 189 | 70 | 72 | 662 | 70 |
| Complex | 16 | 333 | 132 | 34 | 680 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 928148 | 15157 | 16186 | 4550 | 640 |
| Step | 7174 | 14461 | 521 | 598 | 480 |
| Impluse | 3623 | 578 | 5062 | 210 | 354 |
| Cycle | 400 | 63 | 98 | 442 | 60 |
| Complex | 73 | 506 | 202 | 48 | 366 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 914919 | 23245 | 20767 | 4663 | 1087 |
| Step | 4413 | 16123 | 612 | 449 | 1637 |
| Impluse | 1519 | 175 | 6526 | 225 | 1382 |
| Cycle | 359 | 58 | 94 | 477 | 75 |
| Complex | 13 | 234 | 123 | 52 | 773 |
| Actual Class | Classification Results | ||||
|---|---|---|---|---|---|
| Unchanged | Step | Impluse | Cycle | Complex | |
| Unchanged | 953546 | 5456 | 4940 | 704 | 35 |
| Step | 2383 | 20500 | 56 | 58 | 237 |
| Impluse | 829 | 37 | 8863 | 8 | 90 |
| Cycle | 249 | 7 | 5 | 801 | 1 |
| Complex | 3 | 329 | 13 | 1 | 849 |
| Indices (%) | NORCAMA | KLD | KS2 | Proposed |
|---|---|---|---|---|
| Unchanged | ||||
| precision | 99.35 | 98.80 | 99.32 | 99.64 |
| recall | 98.17 | 96.21 | 94.84 | 98.85 |
| F1-score | 98.76 | 97.49 | 97.03 | 99.24 |
| Step change | ||||
| precision | 65.35 | 47.00 | 40.47 | 77.86 |
| recall | 81.18 | 62.24 | 69.39 | 88.23 |
| F1-score | 72.41 | 53.56 | 51.13 | 82.72 |
| Impulse change | ||||
| precision | 51.55 | 22.94 | 23.21 | 63.87 |
| recall | 75.32 | 51.51 | 66.41 | 90.19 |
| F1-score | 61.21 | 31.74 | 34.39 | 74.78 |
| Cycle change | ||||
| precision | 27.94 | 7.56 | 8.13 | 50.95 |
| recall | 62.28 | 41.58 | 44.87 | 75.35 |
| F1-score | 38.58 | 12.79 | 13.77 | 60.80 |
| Complex change | ||||
| precision | 55.37 | 19.26 | 15.60 | 70.05 |
| recall | 56.90 | 30.63 | 64.69 | 71.05 |
| F1-score | 56.13 | 23.65 | 25.14 | 70.54 |
| Macro F1-score | 65.41 | 43.85 | 44.29 | 77.62 |
| Micro F1-score | 97.46 | 94.85 | 93.88 | 98.46 |
| Efficiency | NORCAMA | NOR_KLD | NOR_KS2 | Proposed |
|---|---|---|---|---|
| runtime | 582 s | 776 s | 923 s | 48 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Lv, X.; Dou, F.; Yao, J. Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images. Remote Sens. 2019, 11, 926. https://doi.org/10.3390/rs11080926
Yuan J, Lv X, Dou F, Yao J. Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images. Remote Sensing. 2019; 11(8):926. https://doi.org/10.3390/rs11080926
Chicago/Turabian StyleYuan, Jili, Xiaolei Lv, Fangjia Dou, and Jingchuan Yao. 2019. "Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images" Remote Sensing 11, no. 8: 926. https://doi.org/10.3390/rs11080926
APA StyleYuan, J., Lv, X., Dou, F., & Yao, J. (2019). Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images. Remote Sensing, 11(8), 926. https://doi.org/10.3390/rs11080926