Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS
Abstract
:1. Introduction
2. Model for Inter-System Bias Estimation and Descriptions of the Stochastic Models
2.1. Model for Inter-System Bias Estimation and Processing Strategies
- (a)
- One-step state prediction:
- (b)
- One-step prediction of covariance:
- (c)
- Filtering gain:
- (d)
- Status update:
- (e)
- State covariance update:where is transition matrix; is the coefficient matrix of observation equation; and is the variance matrix of system noise sequence and variance matrix of observation noise, respectively; and is one-step prediction value and its variance-covariance matrix, respectively; is gain matrix; and is filtered estimation and its variance-covariance matrix, respectively; denotes the unit matrix.
2.2. The Different Stochastic Models
- Neglecting inter-system bias between GPS and BDS is named ISB-OFF, which means the positioning model of BDS and GPS is separated, and the two systems are processed without any relation. The BDS observations are processed the same as GPS ones. However, the ISB between GPS and BDS will remain in the BDS processing model and will be reflected in the pseudorange residuals. The configuration equation can be expressed as:where is the ISB in the scheme ISB-OFF. to is an empty matrix which means without considering ISB.
- Estimating the ISB as a piece-wise constant every 30 min (ISB-PW). ISB parameter is initialized at the first epoch, then re-initialized, and updated every 30 min [9]. The configuration equation can be written as:where means the ISB in the scheme ISB-PW. The ISB in one 3-h processing-arc-window can be divided into six parts according to size of piece-wise (every 30 min), which are denoted as to . is one piece-wise ISB, and is from 1 to 6.
- Estimating the ISB as a random-walk processing (ISB-RW). With this scheme, ISB is initialized at the first epoch, and then with a time-related spectral density of 0.001 . The configuration equation can be formed as:where is the ISB in the scheme ISB-RW. is the ISB for one epoch, with from 1 to 360. means the time-related spectral density.
- Estimating the ISB as a processing-arc-dependent constant (ISB-AD). During the whole processing-arc period, ISB is only initialized at the first epoch. If the processing-arc window is one day, this means the ISB is estimated as a constant each day. In this paper, we make the period of our processing tests as 3 h, so the ISB is considered to be a 3-h arc-dependent constant. The configuration equation can be indicated as:where means the ISB in the scheme ISB-AD, which is estimated as a constant during the 3-h processing-arc window.
- Estimating the ISB as white noise (ISB-WN). In this way, the ISB is initialized for each epoch, which is the same as the normal processing mode as the receiver clock error. The configuration equation can be shown as:where means the ISB in the scheme ISB-WN. The ISB in each epoch will be initialized and estimated.
3. Experimental Data
4. Results and Discussion
4.1. Pseudorange and Carrier-Phase Observation Residuals
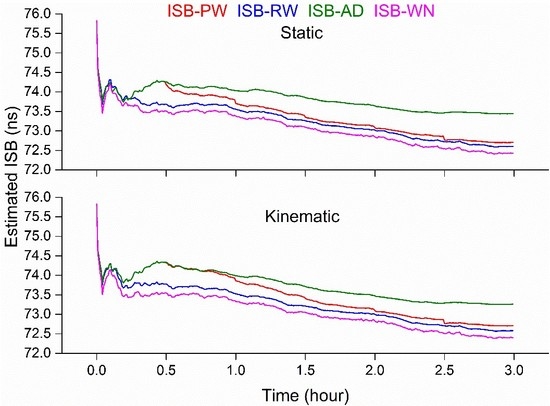
4.2. Comparison of Estimated Inter-System Bias
4.3. Convergence Time and Positioning Accuracy
4.3.1. The Case with GBM Precise Products
4.3.2. The Case with WUM Precise Products
4.4. Accuracy Improvement during the Convergence Period
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aboul-Enein, Y.H. The Precision Revolution: GPS and the Future of Aerial Warfare. Tech. Cult. 2003, 45, 883–884. [Google Scholar]
- Revnivykh, S. GLONASS Status and Progress. In Proceedings of the ION GNSS 2010, Portland, OR, USA, 22 September 2010; pp. 609–633. [Google Scholar]
- Falcone, M. GALILEO System Status. In Proceedings of the ION GNSS 2016, Portland, OR, USA, 12–16 September 2016; pp. 2410–2430. [Google Scholar]
- Yang, Y. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System. Acta Geod. Cartogr. Sin. 2010, 39, 1–6. [Google Scholar]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.B.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. In Proceedings of the 4th International Colloquium on Scientific and Fundamental Aspects of the Galileo System, Prague, Czech Republic, 4–6 December 2013. [Google Scholar]
- Torre, A.D.; Caporali, A. An analysis of intersystem biases for multi-GNSS positioning. GPS Solut. 2015, 19, 297–307. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Hessels, U. Characterization of GPS/GIOVE sensor stations in the CONGO network. GPS Solut. 2011, 15, 193–205. [Google Scholar] [CrossRef]
- Jiang, N.; Xu, Y.; Xu, T.; Xu, G.; Sun, Z.; Schuh, H. GPS/BDS short-term ISB modelling and prediction. GPS Solut. 2017, 21, 163–175. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zhang, Y.; Yang, S.; Chen, Q.; Gong, X. Modeling and Assessment of GPS/BDS Combined Precise Point Positioning. Sensors 2016, 16, 1151. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328. [Google Scholar] [CrossRef] [Green Version]
- Paziewski, J.; Wielgosz, P. Assessment of GPS + Galileo and multi-frequency Galileo single-epoch precise positioning with network corrections. GPS Solut. 2014, 18, 571–579. [Google Scholar] [CrossRef]
- Li, X.; Zus, F.; Lu, C.; Ning, T.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Retrieving high-resolution tropospheric gradients from multiconstellation GNSS observations. Geophys. Res. Lett. 2015, 42, 4173–4181. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geodesy 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Geng, J.; Li, X.; Zhao, Q.; Li, G. Inter-system PPP ambiguity resolution between GPS and BeiDou for rapid initialization. J. Geodesy 2019, 93, 383–398. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Chang, H.; Li, X. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS. J. Geodesy 2018. [Google Scholar] [CrossRef]
- Gioia, C.; Borio, D. A statistical characterization of the Galileo-to-GPS inter-system bias. J. Geodesy 2016, 60, 1279–1291. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Lutz, S.; Meindl, M.; Beutler, G. Combining the Observations from Different GNSS. Presented at the EUREF 2010 Symposium, Gävle, Sweden, 2–5 June 2010; Volume 12. [Google Scholar]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geodesy 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Defraigne, P.; Bruyninx, C. On the link between GPS pseudorange noise and day-boundary discontinuities in geodetic time transfer solutions. GPS Solut. 2007, 11, 239–249. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geodesy 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Xu, G.; Xu, Y. GPS: Theory, Algorithms Application; Springer Publishing Company: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Koch, K.; Yang, Y. Robust Kalman filter for rank deficient observation models. J. Geodesy 1998, 72, 436–441. [Google Scholar] [CrossRef]
- Yang, Y. Adaptively robust kalman filters with applications in navigation. In Sciences Geodesy-I; Springer: Berlin/Heidelberg, Germany, 2010; pp. 49–82. [Google Scholar]
- Hatch, R. The synergism of GPS code and carrier measurements. In Proceedings of the International Geodetic Symposium on Satellite Doppler Positioning; Physical Science Laboratory of the New Mexico State University: Las Cruces, NM, USA, 1983; pp. 1213–1231. [Google Scholar]
- Melbourne, W. The case for ranging in GPS-based geodetic systems. In Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Wubbena, G. Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements. In Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, MD, USA, 15–19 April 1985; pp. 403–412. [Google Scholar]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wu, S.; Hajj, G.; Bertiger, W.; Lichten, S. Effects of antenna orientation on GPS carrier phase. Astrodynamics 1992, 1, 1647–1660. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions. In Proceedings of IERS Technical Note 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt, Germany, 2010; Available online: https://www.iers.org/SharedDocs/Publikationen/EN/IERS/Publications/tn/TechnNote36/tn36.pdf;jsessionid=75EE4C0EE29A43CF4E0A45B6AA441D1A.live2?__blob=publicationFile&v=1 (accessed on 25 April 2019).
- de Oliveira, P.S., Jr.; Morel, L.; Fund, F.; Legros, R.; Monico, J.F.G.; Durand, S.; Durand, F. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar]
- Bree, R.J.P.V.; Tiberius, C.C.J.M. Real-time single-frequency precise point positioning: Accuracy assessment. GPS Solut. 2012, 16, 259–266. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Ge, M.; Li, P.; Wickert, J.; Schuh, H. Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 19. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophys. Res. Solid Earth 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Shi, C.; Yi, W.; Song, W.; Lou, Y.; Yao, Y.; Zhang, R. GLONASS pseudorange inter-channel biases and their effects on combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 439–451. [Google Scholar]










| Item | Models/Strategies |
|---|---|
| Data | GPS + BDS, 8 stations |
| Processing-arc-window | 3 h, 8 stations in one-week period have totally 448 tests |
| Signal selection | GPS:L1 and L2; BDS:B1 and B2 |
| Estimator | Kalman filter |
| Elevation cut off | 7° |
| Interval rate | 30 s |
| Satellite orbit and clock | Fixed to MGEX (GBM or WUM) products |
| Tropospheric delay | Saastamoinen model corrected for the dry component; estimate the residual wet component with random-walk processing |
| Mapping function | Global Mapping Function (GMF) |
| Ionospheric delay | First-order effect eliminated by ionospheric-free linear combination |
| Receiver phase center | PCO and PCV for GPS from igs14.atx are used; Corrections of BDS is applied the same with GPS |
| Satellite phase center | PCO and PCV are used with igs14.atx |
| ISB | Schemes ISB-OFF, ISB-PW, ISB-RW, ISB-AD, ISB-WN |
| Phase ambiguities | Estimated as a constant for each arc |
| Schemes | Descriptions |
|---|---|
| ISB-OFF | Neglecting inter-system bias |
| ISB-PW | Estimating the ISB as piece-wise constant |
| ISB-RW | Estimating the ISB as a random-walk processing |
| ISB-AD | Estimating the ISB as a processing-arc-dependent constant |
| ISB-WN | Estimating the ISB as white noise |
| Station ID | Location | Receiver Type | ||
|---|---|---|---|---|
| Latitude (°) | Longitude (°) | Height (m) | ||
| CUT0 | −32.0039 | 115.8948 | 24.000 | TRIMBLE NETR9 |
| KARR | −20.9814 | 117.0972 | 109.247 | TRIMBLE NETR9 |
| MRO1 | −26.6966 | 116.6375 | 354.069 | TRIMBLE NETR9 |
| PERT | −31.8019 | 115.8852 | 12.920 | TRIMBLE NETR9 |
| MOBS | −37.8294 | 144.9753 | 40.578 | SEPT POLARX4TR |
| NNOR | −31.0487 | 116.1927 | 234.984 | SEPT POLARX4 |
| STR1 | −35.3155 | 149.0109 | 800.032 | SEPT POLARX5 |
| YAR2 | −29.0466 | 115.3470 | 241.291 | SEPT POLARX4TR |
| Static (95%) | Static (68%) | Kinematic (95%) | Kinematic (68%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| OFF | 8.5 | - | 20.0 | 7.5 | 74.5 | 16.0 | 14.5 | - | - | 11.5 | - | 25.0 |
| PW | 5.0 | 63.0 | 31.0 | 4.5 | 45.5 | 31.0 | 7.5 | 72.5 | 34.5 | 6.0 | 63.5 | 25.5 |
| RW | 5.0 | 13.0 | 13.5 | 4.0 | 11.5 | 12.0 | 7.0 | 20.5 | 18.0 | 5.5 | 16.0 | 14.0 |
| AD | 5.0 | - | - | 4.5 | - | - | 7.5 | - | - | 6.0 | - | 25.5 |
| WN | 5.0 | 13.5 | 14.0 | 4.5 | 11.5 | 12.0 | 7.5 | 19.5 | 17.5 | 5.5 | 17.5 | 13.5 |
| Static (95%) | Static (68%) | Kinematic (95%) | Kinematic (68%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| OFF | 9.5 | 31.9 | 23.6 | 1.3 | 9.3 | 4.3 | 14.6 | 34.6 | 31.8 | 4.6 | 12.7 | 10.7 |
| PW | 1.4 | 3.6 | 3.9 | 0.7 | 1.6 | 1.8 | 2.9 | 6.7 | 8.6 | 1.4 | 3.0 | 3.8 |
| RW | 1.2 | 1.6 | 2.7 | 0.7 | 0.7 | 1.3 | 2.0 | 3.0 | 5.8 | 0.8 | 1.3 | 2.6 |
| AD | 12.0 | 36.3 | 34.3 | 3.6 | 18.9 | 12.8 | 19.1 | 50.6 | 43.8 | 7.9 | 24.8 | 19.8 |
| WN | 1.2 | 1.6 | 2.8 | 0.7 | 0.7 | 1.3 | 2.0 | 3.0 | 5.8 | 0.8 | 1.3 | 2.6 |
| Convergence Time (95%)/min | Convergence Time (68%)/min | Accuracy (95%)/cm | Accuracy (68%)/cm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| OFF | 7.5 | 17.5 | 17.0 | 6.5 | 15.5 | 13.0 | 4.9 | 6.1 | 7.6 | 2.0 | 2.7 | 3.2 |
| PW | 7.0 | 14.0 | 14.0 | 5.0 | 12.5 | 12.0 | 4.8 | 6.6 | 7.6 | 2.0 | 2.9 | 3.2 |
| RW | 7.0 | 21.0 | 14.5 | 5.5 | 17.5 | 12.5 | 5.0 | 7.0 | 7.8 | 2.1 | 3.3 | 3.3 |
| AD | 7.0 | 14.0 | 14.0 | 5.0 | 12.5 | 12.0 | 4.8 | 6.2 | 7.4 | 2.0 | 2.7 | 3.1 |
| WN | 7.0 | 23.5 | 14.5 | 5.5 | 19.0 | 12.5 | 5.2 | 6.8 | 8.0 | 2.2 | 3.3 | 3.3 |
| 8 min (95%) | 16 min (95%) | 8 min (68%) | 16 min (68%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| OFF | 71.4 | 78.4 | 191.8 | 76.1 | 94.7 | 178.7 | 49.3 | 57.9 | 106.1 | 35.6 | 45.5 | 76.4 |
| PW | 58.2 | 69.3 | 135.6 | 43.3 | 58.8 | 100.0 | 24.6 | 31.4 | 58.1 | 18.1 | 27.1 | 42.7 |
| RW | 58.7 | 71.2 | 135.9 | 42.9 | 53.1 | 99.0 | 24.3 | 30.6 | 57.4 | 17.6 | 23.7 | 41.5 |
| AD | 58.2 | 69.3 | 135.6 | 43.4 | 58.8 | 100.0 | 24.6 | 31.4 | 58.1 | 18.1 | 27.1 | 42.7 |
| WN | 60.5 | 69.9 | 137.1 | 43.8 | 54.3 | 99.2 | 24.6 | 31.1 | 57.5 | 17.8 | 24.3 | 41.5 |
| 8 min (95%) | 16 min (95%) | 8 min (68%) | 16 min (68%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| OFF | 104.8 | 122.8 | 247.2 | 51.3 | 59.7 | 137.7 | 32.1 | 38.7 | 82.0 | 23.0 | 29.1 | 58.6 |
| PW | 59.2 | 68.7 | 136.9 | 42.0 | 52.0 | 97.6 | 25.3 | 30.5 | 57.0 | 18.2 | 22.9 | 41.0 |
| RW | 59.3 | 68.2 | 136.8 | 42.5 | 55.5 | 98.0 | 25.4 | 31.4 | 57.0 | 18.4 | 24.3 | 41.1 |
| AD | 59.2 | 68.7 | 136.9 | 42.0 | 52.0 | 97.6 | 25.3 | 30.5 | 57.0 | 18.2 | 22.9 | 41.0 |
| WN | 59.6 | 73.4 | 137.0 | 43.2 | 57.6 | 98.8 | 25.7 | 32.5 | 57.6 | 18.6 | 25.6 | 41.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, N.; Xu, T.; Xu, Y.; Xu, G.; Schuh, H. Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS. Remote Sens. 2019, 11, 989. https://doi.org/10.3390/rs11080989
Jiang N, Xu T, Xu Y, Xu G, Schuh H. Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS. Remote Sensing. 2019; 11(8):989. https://doi.org/10.3390/rs11080989
Chicago/Turabian StyleJiang, Nan, Tianhe Xu, Yan Xu, Guochang Xu, and Harald Schuh. 2019. "Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS" Remote Sensing 11, no. 8: 989. https://doi.org/10.3390/rs11080989
APA StyleJiang, N., Xu, T., Xu, Y., Xu, G., & Schuh, H. (2019). Assessment of Different Stochastic Models for Inter-System Bias between GPS and BDS. Remote Sensing, 11(8), 989. https://doi.org/10.3390/rs11080989