Dimensionality Reduction of Hyperspectral Image Using Spatial-Spectral Regularized Sparse Hypergraph Embedding
Abstract
:1. Introduction
2. Related Works
2.1. Graph Embedding
2.2. Hypergraph Model
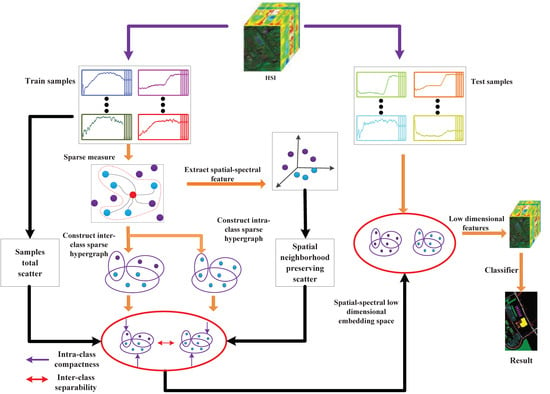
3. SSRHE
3.1. The Regularized Sparse Hypergraph Model
3.2. Spatial-Spectral Hypergraph Embedding
| Algorithm 1 SSRHE. |
Input: HSI dataset , corresponding class label set , tradeoff parameters , , weighted coefficient , spatial neighborhood size T, reduced dimensionality d.
|
4. Experimental Results and Discussion
4.1. HSI Datasets
4.2. Experimental Setup
4.3. Parameters Selection
4.4. Investigation of Embedding Dimension
4.5. Investigation of Classification Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liao, D.; Qian, Y.; Tang, Y.Y. Constrained manifold learning for hyperspectral imagery visualization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 1, 1213–1226. [Google Scholar] [CrossRef]
- Yuan, Q.Q.; Zhang, Q.; Li, J.; Li, J.; Zhang, L.P. Hyperspectral image denoising employing a spatial-spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, Y.; Hang, R.; Song, H. Spatial-spectral locality-constrained low-rank representation with semi-supervised hypergraph learning for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4171–4182. [Google Scholar] [CrossRef]
- Zhang, X.R.; Gao, Z.Y.; Jiao, L.C.; Zhou, H.Y. Multifeature hyperspectral image classification with local and nonlocal spatial information via markov random field in semantic space. IEEE Trans. Geosci. Remote Sens. 2016, 56, 1409–1424. [Google Scholar] [CrossRef]
- Xu, Y.H.; Zhang, L.P.; Du, B.; Zhang, F. Spectral-spatial unified networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5893–5909. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O. Spectral contextual classification of hyperspectral imagery with probabilistic relaxation labeling. IEEE Trans. Cybern. 2017, 47, 4380–4391. [Google Scholar] [CrossRef] [PubMed]
- Hang, R.; Liu, Q.; Sun, Y.; Yuan, X.; Pei, H.; Plaza, J.; Plaza, A. Robust matrix discriminative analysis for feature extraction from hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2002–2011. [Google Scholar] [CrossRef]
- Luo, F.L.; Huang, H.; Ma, Z.Z.; Liu, J.M. Semi-supervised sparse manifold discriminative analysis for feature extraction of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6197–6221. [Google Scholar] [CrossRef]
- Xu, J.; Yang, G.; Yin, Y.F.; Man, H.; He, H.B. Sparse representation based classification with structure preserving dimension reduction. Cogn. Comput. 2014, 6, 608–621. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.C.; Yang, M.Q.; Zhang, Y.; Wang, J.; Marshall, S.; Han, J.W. Novel folded-PCA for improved feature extraction and data reduction with hyperspectral imaging and SAR in remote sensing. ISPRS J. Photogramm. Remote Sens. 2014, 93, 112–122. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Noise-adjusted subspace discriminant analysis for hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1374–1378. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, L.; Bu, J.; Wang, C.; Chen, W. Constrained laplacian eigenmap for dimensionality reduction. Neurocomputing 2010, 73, 951–958. [Google Scholar] [CrossRef]
- Bachmann, C.M.; Ainsworth, T.L.; Fusina, R.A. Exploiting manifold geometry in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 441–454. [Google Scholar] [CrossRef]
- He, X.F.; Cai, D.; Yan, S.C.; Zhang, H.J. Neighborhood preserving embedding. In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 2, pp. 1208–1213. [Google Scholar]
- Zheng, Z.L.; Yang, F.; Tan, W.; Jia, J.; Yang, J. Gabor feature-based face recognition using supervised locality preserving projection. Signal Process. 2007, 87, 2473–2483. [Google Scholar] [CrossRef]
- Huang, H.; Yang, M. Dimensionality reduction of hyperspectral images with sparse discriminant embedding. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5160–5169. [Google Scholar] [CrossRef]
- Jiang, X.; Song, X.; Zhang, Y.; Jiang, J.; Gao, J.; Cai, Z. Laplacian regularized spatial-aware collaborative graph for discriminant analysis of hyperspectral imagery. Remote Sens. 2019, 11, 29. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q. Dimensionality reduction of hyperspectral image using spatial regularized local graph discriminant embedding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3262–3271. [Google Scholar] [CrossRef]
- Feng, F.B.; Li, W.; Du, Q.; Zhang, B. Dimensionality reduction of hyperspectral image with graph-based discriminant analysis considering spectral similarity. Remote Sens. 2017, 9, 323. [Google Scholar] [CrossRef]
- Luo, F.L.; Huang, H.; Duan, Y.L.; Liu, J.M.; Liao, Y.H. Local geometric structure feature for dimensionality reduction of hyperspectral imagery. Remote Sens. 2017, 9, 790. [Google Scholar] [CrossRef]
- Sugiyama, M. Dimensionality reduction of multimodal labeled data by local fisher discriminant analysis. J. Mach. Learn. Res. 2007, 8, 1027–1061. [Google Scholar]
- Zhou, Y.C.; Peng, J.T.; Philip Chen, L.C. Dimension reduction using spatial and spectral regularized local discriminant embedding for hyperspectral image classification. IEEE Trans. Geosic. Remote Sens. 2015, 53, 1082–1095. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Q.; Zhang, S.; Metaxas, D. Image retrieval via probabilistic hypergraph ranking. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3367–3383. [Google Scholar]
- Liu, Q.; Sun, Y.; Wang, C.; Liu, T.; Tao, D. Elastic net hypergraph learning for image clustering and semi-supervised classification. IEEE Trans. Image Process. 2017, 26, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Tao, D.; Wang, M. Adaptive hypergraph learning and its application in image classification. IEEE Trans. Image Process. 2012, 21, 3262–3272. [Google Scholar]
- Wang, W.H.; Qian, Y.T.; Tang, Y.Y. Hypergraph-regularized sparse NMF for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 681–694. [Google Scholar] [CrossRef]
- Huang, S.; Yang, D.; Ge, Y.X.; Zhang, X.H. Discriminant hyper-Laplacian projection and its scalable extension for dimensionality reduction. Neurocomputing 2016, 173, 145–153. [Google Scholar] [CrossRef]
- Du, W.B.; Qiang, W.W.; Lv, M.; Hou, Q.L.; Zhen, L.; Jing, L. Semi-supervised dimension reduction based on hypergraph embedding for hyperspectral images. Int. J. Remote Sens. 2018, 39, 1696–1712. [Google Scholar] [CrossRef]
- Gao, S.H.; Tsang, I.W.H.; Chia, L.T. Laplacian sparse coding, hypergraph Laplacian sparse coding, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 92–104. [Google Scholar] [CrossRef] [PubMed]
- Pio, G.; Serafino, F.; Malerba, D.; Ceci, M. Multi-type clustering and classification from heterogeneous networks. Inf. Sci. 2018, 425, 107–126. [Google Scholar] [CrossRef]
- Serafino, F.; Pio, G.; Ceci, M. Ensemble learning for multi-type classification in heterogeneous networks. IEEE Trans. Knowl. Data Eng. 2018, 30, 2326–2339. [Google Scholar] [CrossRef]
- Liao, W.Z.; Mura, M.D.; Chanussot, J.; Pizurica, A. Fusion of spectral and spatial information for classification of hyperspectral remote sensed imagery by local graph. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 9, 583–594. [Google Scholar] [CrossRef]
- Zhao, J.; Zhong, Y.F.; Shu, H.; Zhang, L.P. High-resolution image classification integrating spectral-spatial-location cues by conditional random fields. IEEE Trans. Image Process. 2016, 25, 4033–4045. [Google Scholar] [CrossRef]
- Cao, J.; Wang, B. Embedding learning on spectral-spatial graph for semi-supervised hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1805–1809. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral-spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Wu, Z.B.; Shi, L.L.; Li, J.; Wang, Q.C.; Sun, L.; Wei, Z.H.; Plaza, J.; Plaza, A.J. GPU parallel implementation of spatially adaptive hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1131–1143. [Google Scholar] [CrossRef]
- Mohan, A.; Sapion, G.; Bosch, E. Spatially coherent nonlinear dimensionality reduction and segmentation of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2007, 4, 206–210. [Google Scholar] [CrossRef]
- Huang, H.; Zheng, X.L. Hyperspectral image land cover classification algorithm based on spatial-spectral coordination embedding. Acta Geod. Cartogr. Sin. 2016, 4, 964–972. [Google Scholar]
- Feng, Z.X.; Yang, S.Y.; Wang, S.G.; Jiao, L.C. Discriminative spectral-spatial margin-based semisupervised dimensionality reduction of hyperspectral data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 224–228. [Google Scholar] [CrossRef]
- Ji, R.R.; Gao, Y.; Hong, R.C.; Liu, Q.; Tao, D.C.; Li, X.L. Spectral-spatial constraint hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1811–1824. [Google Scholar]
- Luo, F.L.; Du, B.; Zhang, L.P.; Zhang, L.F.; Tao, D.C. Feature learning using spatial-spectral hypergraph discriminant analysis for hyperspectral image. IEEE Trans. Cybern. 2019, 49, 2406–2419. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Lu, Y.; Yuan, H. Hyperspectral image classification based on three-dimensional scattering wavelet transform. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2467–2480. [Google Scholar] [CrossRef]
- Sun, Y.B.; Wang, S.J.; Liu, Q.S.; Hang, R.L.; Liu, G.C. Hypergraph embedding for spatial-spectral joint feature extraction in hyperspectral images. Remote Sens. 2017, 9, 506. [Google Scholar]
- Yuan, H.L.; Tang, Y.Y. Learning with hypergraph for hyperspectral image feature extraction. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1695–1699. [Google Scholar] [CrossRef]
- Sun, Y.; Hang, R.; Liu, Q.; Zhu, F.; Pei, H. Graph-rRegularized low rank representation for aerosol optical depth retrieval. Int. J. Remote Sens. 2016, 37, 5749–5762. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, Z.; Chen, Y.; Yang, J. Spatial-Spectral graph regularized kernel sparse representation for hyperspectral image classification. ISPRS Int. J. Geo-Inf. 2017, 6, 258. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Li, J.; Li, H.C.; Deng, C.Z.; Antonio, P. Spectral-spatial weighted sparse regression for hyperspectral image unmixing. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3265–3276. [Google Scholar] [CrossRef]
- Sun, W.W.; Zhang, L.F.; Zhang, L.P.; Yenming, M.L. A dissimilarity-weighted sparse self-representation method for band selection in hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4374–4388. [Google Scholar] [CrossRef]
- Luo, M.N.; Zhang, L.L.; Liu, J.; Zheng, Q.H. Distributed extreme learning machine with alternating direction method of multiplier. Neurocomputing 2017, 261, 164–170. [Google Scholar] [CrossRef]











| Method | 5 | 20 | 50 | 100 | 200 |
|---|---|---|---|---|---|
| RAW | 43.6 ± 2.8 (0.372) | 54.9 ± 1.7 (0.495) | 60.1 ± 1.4 (0.552) | 63.6 ± 0.9 (0.588) | 66.9 ± 0.6 (0.622) |
| PCA | 43.4 ± 2.7 (0.370) | 54.9 ± 1.6 (0.495) | 60.2 ± 1.2 (0.553) | 63.9 ± 0.8 (0.591) | 67.0 ± 0.6 (0.622) |
| LDA | 32.5 ± 4.8 (0.253) | 51.6 ± 1.9 (0.459) | 64.4 ± 1.2 (0.599) | 71.0 ± 0.5 (0.672) | 74.4 ± 0.7 (0.706) |
| LPP | 43.6 ± 3.7 (0.372) | 54.5 ± 1.8 (0.491) | 59.7 ± 1.2 (0.546) | 62.7 ± 1.0 (0.578) | 65.8 ± 0.5 (0.609) |
| MFA | 44.1 ± 4.0 (0.377) | 57.1 ± 1.6 (0.520) | 66.8 ± 1.9 (0.625) | 70.8 ± 1.1 (0.669) | 72.0 ± 1.0 (0.680) |
| RLDE | 41.7 ± 1.1 (0.622) | 60.9 ± 1.5 (0.561) | 69.8 ± 1.4 (0.659) | 74.6 ± 0.7 (0.711) | 78.4 ± 0.6 (0.751) |
| DHLP | 44.1 ± 3.8 (0.377) | 57.2 ± 2.1 (0.522) | 68.9 ± 1.2 (0.649) | 73.8 ± 0.8 (0.702) | 77.6 ± 0.7 (0.741) |
| SSCE | 30.2 ± 4.5 (0.230) | 69.7 ± 1.0 (0.658) | 76.3 ± 0.9 (0.730) | 79.1 ± 0.5 (0.760) | 82.9 ± 0.6 (0.801) |
| LPNPE | 60.2 ± 3.5 (0.594) | 74.0 ± 1.4 (0.706) | 79.3 ± 0.7 (0.759) | 81.6 ± 0.6 (0.791) | 84.2 ± 0.6 (0.817) |
| SSRHE | 65.6 ± 2.3 (0.615) | 74.8 ± 1.2 (0.711) | 80.0 ± 1.0 (0.765) | 82.9 ± 1.0 (0.803) | 86.7 ± 1.0 (0.829) |
| Method | 5 | 20 | 50 | 100 | 200 |
|---|---|---|---|---|---|
| RAW | 60.5 ± 4.2 (0.512) | 66.4 ± 2.4 (0.583) | 73.5 ± 1.6 (0.663) | 76.4 ± 0.8 (0.698) | 78.8 ± 0.8 (0.724) |
| PCA | 60.5 ± 4.2 (0.512) | 66.5 ± 2.2 (0.583) | 73.4 ± 1.6 (0.662) | 76.4 ± 0.8 (0.697) | 78.7 ± 0.6 (0.724) |
| LDA | 46.7 ± 6.4 (0.351) | 59.6 ± 1.8 (0.495) | 73.5 ± 1.4 (0.662) | 78.9 ± 0.9 (0.727) | 83.4 ± 0.6 (0.782) |
| LPP | 47.0 ± 5.6 (0.354) | 59.3 ± 2.6 (0.500) | 72.8 ± 2.3 (0.654) | 78.3 ± 1.3 (0.722) | 82.2 ± 1.2 (0.768) |
| MFA | 64.5 ± 4.3 (0.555) | 69.2 ± 4.5 (0.613) | 76.4 ± 2.0 (0.699) | 78.1 ± 2.4 (0.715) | 79.1 ± 2.2 (0.730) |
| RLDE | 64.4 ± 3.2 (0.555) | 74.6 ± 2.7 (0.677) | 77.9 ± 2.2 (0.718) | 82.1 ± 1.0 (0.770) | 84.8 ± 1.0 (0.802) |
| DHLP | 56.8 ± 8.0 (0.471) | 62.2 ± 3.6 (0.530) | 70.8 ± 2.1 (0.629) | 77.5 ± 2.7 (0.711) | 80.2 ± 1.5 (0.742) |
| SSCE | 42.3 ± 5.3 (0.309) | 63.3 ± 2.9 (0.543) | 75.8 ± 1.7 (0.692) | 82.7 ± 1.2 (0.804) | 87.0 ± 0.8 (0.828) |
| LPNPE | 68.0 ± 4.2 (0.606) | 80.0 ± 2.2 (0.747) | 86.3 ± 1.3 (0.822) | 87.9 ± 0.9 (0.842) | 89.9 ± 0.6 (0.877) |
| SSRHE | 71.6 ± 2.7 (0.646) | 82.6 ± 2.3 (0.776) | 87.5 ± 1.1 (0.837) | 90.0 ± 1.5 (0.882) | 92.2 ± 0.2 (0.908) |
| Class | Train | Test | RAW | PCA | LDA | LPP | MFA | RLDE | DHLP | SSCE | LPNPE | SSRHE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 36 | 41.67 | 41.67 | 77.78 | 36.11 | 50.00 | 61.11 | 63.89 | 55.56 | 77.78 | 94.44 |
| 2 | 143 | 1285 | 53.39 | 52.45 | 64.12 | 51.05 | 56.03 | 72.14 | 66.69 | 60.31 | 80.78 | 88.17 |
| 3 | 83 | 747 | 57.30 | 55.29 | 57.70 | 47.12 | 50.07 | 61.58 | 61.58 | 63.45 | 74.30 | 80.46 |
| 4 | 24 | 213 | 41.78 | 44.60 | 52.58 | 43.19 | 21.60 | 58.69 | 59.15 | 51.17 | 77.00 | 84.04 |
| 5 | 48 | 435 | 78.85 | 78.62 | 89.43 | 77.93 | 78.85 | 86.90 | 87.82 | 80.46 | 91.72 | 96.55 |
| 6 | 73 | 657 | 90.26 | 89.50 | 95.74 | 91.02 | 94.67 | 95.28 | 95.89 | 94.52 | 96.04 | 97.02 |
| 7 | 10 | 18 | 77.78 | 88.89 | 100 | 88.89 | 77.78 | 94.44 | 94.44 | 100 | 94.44 | 100 |
| 8 | 48 | 430 | 95.58 | 95.58 | 99.53 | 93.95 | 93.26 | 99.30 | 99.77 | 92.56 | 99.53 | 98.60 |
| 9 | 10 | 10 | 70.00 | 70.00 | 60.00 | 50.00 | 70.00 | 80.00 | 90.00 | 90.00 | 100 | 80.00 |
| 10 | 97 | 875 | 61.03 | 60.46 | 60.91 | 57.49 | 42.06 | 68.91 | 63.20 | 72.11 | 82.74 | 83.89 |
| 11 | 246 | 2209 | 69.76 | 69.85 | 71.89 | 69.62 | 58.85 | 79.36 | 79.22 | 74.02 | 85.92 | 89.50 |
| 12 | 59 | 534 | 39.33 | 37.45 | 65.36 | 32.02 | 47.38 | 67.42 | 62.73 | 50.56 | 87.83 | 83.71 |
| 13 | 21 | 184 | 88.04 | 88.04 | 97.83 | 88.04 | 94.57 | 97.28 | 98.37 | 94.57 | 98.91 | 100 |
| 14 | 127 | 1138 | 94.02 | 93.94 | 94.11 | 92.88 | 90.69 | 96.66 | 95.61 | 93.94 | 96.10 | 95.52 |
| 15 | 39 | 347 | 31.12 | 30.55 | 54.18 | 25.07 | 42.65 | 40.92 | 48.41 | 55.04 | 71.47 | 83.57 |
| 16 | 10 | 83 | 91.57 | 91.57 | 90.36 | 85.54 | 85.54 | 90.36 | 92.77 | 84.34 | 92.77 | 97.59 |
| OA (%) | 68.33 | 67.88 | 74.44 | 65.91 | 64.03 | 78.27 | 77.00 | 74.06 | 87.65 | 89.78 | ||
| AA (%) | 67.59 | 68.03 | 76.97 | 64.37 | 65.87 | 78.15 | 78.72 | 75.79 | 88.02 | 90.88 | ||
| KC | 0.638 | 0.633 | 0.707 | 0.609 | 0.589 | 0.751 | 0.736 | 0.704 | 0.858 | 0.884 | ||
| Class | Train | Test | RAW | PCA | LDA | LPP | MFA | RLDE | DHLP | SSCE | LPNPE | SSRHE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 332 | 6299 | 85.62 | 85.62 | 87.68 | 87.82 | 82.76 | 90.19 | 63.89 | 89.73 | 90.20 | 91.19 |
| 2 | 933 | 17,716 | 94.65 | 94.57 | 94.88 | 94.76 | 93.90 | 97.73 | 66.69 | 96.70 | 97.53 | 98.12 |
| 3 | 105 | 1994 | 65.15 | 64.64 | 63.34 | 67.00 | 61.84 | 74.77 | 61.58 | 72.37 | 77.28 | 78.6 |
| 4 | 154 | 2910 | 77.22 | 77.36 | 81.79 | 79.01 | 77.02 | 84.13 | 59.15 | 84.78 | 87.83 | 89.26 |
| 5 | 68 | 1277 | 98.83 | 98.83 | 98.84 | 99.30 | 99.77 | 99.53 | 87.82 | 99.37 | 99.77 | 99.77 |
| 6 | 252 | 4777 | 60.26 | 60.32 | 65.17 | 65.47 | 69.72 | 70.36 | 95.89 | 73.86 | 89.68 | 85.22 |
| 7 | 67 | 1263 | 75.30 | 75.30 | 66.67 | 75.69 | 71.26 | 80.36 | 94.4 | 88.60 | 86.06 | 90.18 |
| 8 | 185 | 3497 | 80.27 | 80.27 | 74.39 | 81.42 | 77.36 | 84.79 | 99.77 | 82.85 | 84.68 | 79.33 |
| 9 | 48 | 899 | 100 | 100 | 99.44 | 100 | 99.67 | 100 | 90.00 | 99.78 | 99.89 | 100 |
| OA (%) | 84.92 | 84.88 | 85.40 | 86.27 | 84.73 | 89.70 | 78.00 | 89.60 | 91.30 | 92.59 | ||
| AA (%) | 81.92 | 81.88 | 81.47 | 83.38 | 81.48 | 86.87 | 77.72 | 87.56 | 89.53 | 90.55 | ||
| KC | 0.797 | 0.796 | 0.804 | 0.815 | 0.796 | 0.861 | 0.736 | 0.861 | 0.883 | 0.902 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Chen, M.; Duan, Y. Dimensionality Reduction of Hyperspectral Image Using Spatial-Spectral Regularized Sparse Hypergraph Embedding. Remote Sens. 2019, 11, 1039. https://doi.org/10.3390/rs11091039
Huang H, Chen M, Duan Y. Dimensionality Reduction of Hyperspectral Image Using Spatial-Spectral Regularized Sparse Hypergraph Embedding. Remote Sensing. 2019; 11(9):1039. https://doi.org/10.3390/rs11091039
Chicago/Turabian StyleHuang, Hong, Meili Chen, and Yule Duan. 2019. "Dimensionality Reduction of Hyperspectral Image Using Spatial-Spectral Regularized Sparse Hypergraph Embedding" Remote Sensing 11, no. 9: 1039. https://doi.org/10.3390/rs11091039
APA StyleHuang, H., Chen, M., & Duan, Y. (2019). Dimensionality Reduction of Hyperspectral Image Using Spatial-Spectral Regularized Sparse Hypergraph Embedding. Remote Sensing, 11(9), 1039. https://doi.org/10.3390/rs11091039