Improved Estimation of the Intrinsic Dimension of a Hyperspectral Image Using Random Matrix Theory

Abstract

Many methods have been proposed in the literature for estimating the number of materials/endmembers in a hyperspectral image. This is sometimes called the “intrinsic” dimension (ID) of the image. A number of recent papers have proposed ID estimation methods based on various aspects of random matrix theory (RMT), under the assumption that the errors are uncorrelated, but with possibly unequal variances. A recent paper, which reviewed a number of the better known methods (including one RMT-based method), has shown that they are all biased, especially when the true ID is greater than about 20 or 30, even when the error structure is known. I introduce two RMT-based estimators ($RM{T}_G$, which is new, and $RM{T}_{KN}$, which is a modification of an existing estimator), which are approximately unbiased when the error variances are known. However, they are biased when the error variance is unknown and needs to be estimated. This bias increases as ID increases. I show how this bias can be reduced. The results use semi-realistic simulations based on three real hyperspectral scenes. Despite this, when applied to the real scenes, $RM{T}_G$ and $RM{T}_{KN}$ are larger than expected. Possible reasons for this are discussed, including the presence of errors which are either deterministic, spectrally and/or spatially correlated, or signal-dependent. Possible future research into ID estimation in the presence of such errors is outlined.

1. Introduction

There have been many papers which propose various methods for estimating the number of materials/endmembers in hyperspectral images [1,2,3,4,5,6,7,8,9]. This is sometimes called “virtual dimensionality” [2] and sometimes called “intrinsic dimension” (ID) [10,11]. I will use the latter term. A number of recent papers propose ID estimation methods based on random matrix theory (RMT) [11,12,13,14].

The ID concept is more important in some application areas than in others. It is particularly important in the field of mineral exploration, where there is great interest in distinguishing between minerals differing subtly in their chemistry or crystallinity. Often these differences can be detected spectroscopically; see [15] (Figures 2 and 3), which respectively show subtle spectral differences between different types of white mica (due to chemical substitutions) and different types of kaolin (due to changes in crystallinity). Detecting these differences in mixtures can be quite challenging. In such applications, when a spectral library is unavailable, and a blind unmixing approach is required (e.g., [16,17,18,19,20]), it is useful to have a good estimate of the ID in order to decide on the number of endmembers to use in the unmixing. Even when a library such as the U.S. Geological Survey’s spectral library (http://speclab.cr.usgs.gov/spectral-lib.html) is available, it may be that there are some minerals in the scene which are not in the library. A good estimate of the ID can then be useful in determining whether all the spectrally distinct minerals in the scene have been found.

All the above-mentioned ID estimation methods are based on the linear mixture model, which I now outline. Let $X_i,i=1,\dots ,N$ denote the d-dimensional vector (d-vector for short) of observations at pixel i (out of N) in a hyperspectral image. Under the linear mixture model, if there are $M(<N)$ spectrally distinct materials in the image, then

$$X_i=\sum _{k=1}^M{w}_{ik}{E}_k+{ϵ}_i,i=1,\dots ,N,$$

(1)

where (i) $E_k,k=1,\dots ,M$ (= ID) are the “endmember” d-vectors (i.e., pure materials); (ii) $w_{ik}$ are non-negative weights, and (iii) ${ϵ}_i$ are d-vector error terms. The errors are typically a combination of instrumental noise, natural variation in spectra representing the same material, and small non-linearities in the mixing. I will usually use the term “error”, but sometimes it will be convenient to use the term “noise”.

In all of the papers mentioned in the first paragraph, the errors are assumed to be spatially and spectrally uncorrelated. The error variances are also assumed to be spatially constant. Methods proposed in [1,3,6,7,9,12,13], assume that the errors at each wavelength/band have equal variances. This is unrealistic; figures in two recent papers [21] (Figure 1a,b) and [22] (Figure 3) give estimates of the error variances for the three scenes that I will consider in this paper: AVIRIS [23] Indian Pines and Cuprite scenes, and a HyMap${}^{TM}$ subscene [24] acquired near Mt. Isa, Queensland, Australia. These estimates use the Regression method [25], which [22] (Section III) show is close to the best of three spatial and two spectral error variance estimators considered in that paper. The plots show clearly that the estimated error variances are unequal. Methods proposed in [2,4,5,8,11,14] assume that the error variances are possibly unequal and use several methods to estimate them. The estimated error variances or standard deviations (SDs) are then used to preprocess the data in various ways (e.g., by whitening), before applying the proposed ID method.

Using semi-realistic simulations of four scenes [21] (including the three that will be analysed in this paper), Berman et al. [22] investigate the performance of five ID estimation methods: the Harsanyi-Farrand-Chang method ($HFC$) [1], noise-whitened $HFC$ ($NWHFC$) and noise subspace projection ($NSP$) (both proposed by [2]), hyperspectral signal subspace identification by minimum error ($HySime$) [4] and an RMT-method proposed by [11] (which I will henceforth refer to as $RM{T}_{CN}$, after the lead author of that paper). They find that, even when the error variances are known and used to preprocess the data, $NSP$ consistently overestimates the ID by a large margin, while $HySime$ consistently underestimates the ID somewhat; see [22] (Figure 9a–d). The $HFC$ estimates tend to decrease as the true ID increases. This strange behaviour is probably related to the fact that estimated error variances are not used to preprocess the data first. $NWHFC$ and $RM{T}_{CN}$ perform better than the other three methods. However, they tend to underestimate the true ID. The underestimation becomes worse as the true ID increases, especially above about 20 or 30, depending on which of the four scenes has been simulated.

As mentioned above, Berman et al. [22] also compare three spatial and two spectral error variance estimators. The two spectral error variance estimators significantly outperform the three spatial estimators for all four scenes. One of them, the Modified Regression (MR) estimator [26], is always the best (It is closely followed by the Regression estimator [25]). However, the MR estimator is sometimes a little biased (see [22] (Figure 8a–d)) and can sometimes be negative; see [22] (Figure 7). They provide a simple correction, which they call the Positively Modified Regression (PMR) estimator, to ensure its positivity (although it can still be a little biased). They use this estimator to whiten simulated versions of the four scenes, and then apply the best ID estimator for each of the scenes when the error variances are known ($RM{T}_{CN}$ in three cases and $NWHFC$ in the fourth) to estimate the ID. Not surprisingly, the ID estimates are usually a little worse when the error variances are estimated than when they are known; see [22] (Figure 10a–d).

In this paper, I will show (i) how to remove the bias in ID estimation when the error variances are known, and (ii) how to reduce the bias further when the error variances are estimated by the slightly biased PMR estimator. The first objective will be achieved by a more careful application of random matrix theory. The second will be achieved by first whitening the data using the PMR estimators of the error SDs, and then applying RMT to the first part of the “noise” eigenvalues, where RMT theory still appears to hold reasonably well even though the error variances have been estimated.

The paper is structured as follows. Section 2.1 first discusses the three real hyperspectral scenes and introduces simulated versions of them. Section 2.2 summarises relevant random matrix theory, all of which is based on the behaviour of “noise” eigenvalues when two key assumptions are satisfied. In Section 2.3, the simulations are used to compare five RMT-based estimators and $NWHFC$ when the error variances are known. This demonstrates that $NWHFC$ and two of the RMT-based estimators are significantly biased. The other three estimators appear to be unbiased or minimally biased. In Section 2.4, I investigate the behaviour of the three remaining ID estimators when the simulated data have been whitened using the PMR estimator. One of the three ID estimators is significantly affected by the bias in the PMR estimator. The other two ID estimators (which I call $RM{T}_G$ and $RM{T}_{KN}$) are much less affected by the bias. Plots in Section 2.4 also suggest an adjustment to $RM{T}_G$ and $RM{T}_{KN}$ which reduces their bias a little. This adjustment is introduced in Section 2.5. In Section 3, the five RMT-based estimators (including the adjusted versions of $RM{T}_G$ and $RM{T}_{KN}$), $HySime$ and $NWHFC$ are calculated for the three real images. $RM{T}_G$ and $RM{T}_{KN}$ (and their adjusted versions) are much larger than most of the other estimators for all three scenes. There is a detailed discussion in Section 4 about possible reasons for this. Section 5 summarises the paper and suggests possible future research.

The paper contains three innovations: (i) the introduction of the new $RM{T}_G$ estimator (in Section 2.2.2), which overall performs best; (ii) the modification of the $RM{T}_{KN}$ estimator, by the use of the PMR error variance estimator (in Section 2.4), rather than the error variance estimator used previously [12], and (iii) the introduction of a method for reducing the bias in both estimators caused by the bias in the PMR estimator (in Section 2.5).

2. Materials and Methods

2.1. Three Real Hyperspectral Scenes and Simulated Versions of Them

In this subsection, I summarise information about three real hyperspectral scenes and simulations of them that I will use to (i) exemplify various technical issues and (ii) compare different ID estimation methods. Each of these three scenes highlights different issues that will be discussed at various points in the paper. A more detailed discussion about these three scenes (and a fourth scene, which is not included in this paper because it doesn’t provide additional insights) can be found in [22] (Section II). Relevant summary information about the three scenes is provided in

Table 1. Summary information about three real scenes.

Scene	d	N
Indian Pines	193	21,025
Cuprite	185	314,368
Mt. Isa	124	294,460

.

I will use semi-realistic simulations of these three scenes. More realistic simulations of hyperspectral scenes are being increasingly used [21,27,28,29,30]. Making simulations more realistic makes it easier to check the many assumptions underlying the simulations, the variance estimation methods and the ID estimation methods (e.g., scene type, image size, error/noise assumptions, interactions between the signal and noise), which may subtly affect ID estimates.

At various points in the paper, for each scene, I will use simulations with a single “exemplar” value of M to highlight particular technical issues. I will also use simulations with a range of values of M for each scene to compare different ID estimators. For each scene the chosen range of values has mainly been determined by the range of the ID estimators $HFC,NWHFC,NSP,HySime$ and $RM{T}_{CN}$ for the real scenes on the assumption that the true ID value for that scene lies in that range. Four of these estimators have been introduced in two highly-cited papers [2,4]. Further discussion of this issue can be found in [22] (Section II.B).

2.2. Relevant Random Matrix Theory and a Review of Id Estimators Which Use This Theory

This section reviews random matrix theory that is relevant to various ID estimators (and improvements to them) that will be discussed in Section 2.3, Section 2.4, Section 2.5 and Section 3. Let ${ϵ}_i^T=({ϵ}_{i1},\dots ,{ϵ}_{id}),$ $i=1,\dots ,N$. All the theory that will be reviewed in Section 2.2 makes the following key assumptions:

Assumption 1.

$Var\left({ϵ}_{ij}\right)={\sigma }^2,j=1,\dots ,d;i=1,\dots ,N$, i.e., the band error variances are equal.

Assumption 2.

All the errors are spatially and spectrally uncorrelated.

The review in this section is in (mostly) chronological order.

2.2.1. Marchenko-Pastur Law

This important law is concerned with the asymptotic behaviour of the eigenvalues of the sample covariance matrix of independent noise observations. Let $\mathit{ϵ}=({ϵ}_1,\dots ,{ϵ}_N)$ denote the $d\times N$ noise matrix, and let $\widehat{\mathsf{\Sigma }}=\mathit{ϵ}{\mathit{ϵ}}^T/N$ denote the sample noise covariance matrix. Then [31] show that, under Assumptions 1 and 2, as $d,N\to \infty$ with $d/N\to \rho$, the empirical distribution of the eigenvalues of $\widehat{\mathsf{\Sigma }}$ converges to the Marchenko-Pastur distribution, whose probability density function (pdf) is given by

$$\begin{array}{ccc}\hfill f\left(w\right)& =& \sqrt{(b-w)(w-a)}/\left(2\pi {\sigma }^2\rho w\right),a\le w\le b,\hfill \\ & =& 0,otherwise,\hfill \end{array}$$

(2)

where

$$a={\sigma }^2{(1-\sqrt{\rho })}^2,b={\sigma }^2{(1+\sqrt{\rho })}^2.$$

(3)

I will denote this distribution by MP(${\sigma }^2,\rho$). The cumulative distribution function (cdf) of the MP distribution does not have an analytic form.

The proof of the Marchenko-Pastur law requires the parameter $\rho =li{m}_{N,d\to \infty }(d/N)$. In practice, one sets

$$\rho =d/N.$$

(4)

The Marchenko-Pastur Law also holds when there is signal present, with some minor modifications. Usually one expects that the “signal” eigenvalues will be larger than the “noise” eigenvalues. However, occasionally some signals in the data may be so weak as to be undetectable. Under Assumptions 1 and 2 [12] (Equation (11)) and [11] (Equation (8)) state that there is a threshold value (called the “asymptotic limit of detection” by the former), below which signal eigenvalues cannot be successfully identified, at least asymptotically. This value is

$${\tau }_{crit}={\sigma }^2\sqrt{d/N}.$$

(5)

The proof of this result is contained in [32] (Theorem 1.1).

Hao et al. [21] (Section IV) define the Effective Intrinsic Dimension (EID) as the number of signal eigenvalues greater than ${\tau }_{crit}$. EID is never greater than ID, but the simulations presented below suggest that, for hyperspectral data, EID is sometimes a little less than ID. I believe that EID is the quantity that a good ID estimator should aim to estimate. It will be included in all the plots comparing various ID estimators with simulated data in Section 2.3, Section 2.4, Section 2.5 and Section 3. Where appropriate, I will use the symbol L instead of EID. Note that, when signal is present, the Marchenko-Pastur Law only applies to the (pure) noise eigenvalues, of which there are

$$d_{ϵ}\equiv d-EID=d-L.$$

(6)

I will call $d_{ϵ}$ the “pure noise” dimension.

How well does the MP distribution approximate the noise eigenvalues for simulated versions of the three scenes? The first thing to note is that the noise/error variances for the three scenes do not satisfy Assumption 1; see [21] (Figure 1a,b), which show the estimates of the error SDs for the real and simulated Indian Pines and Cuprite scenes using the Regression method [25]. This is a little worse than the PMR estimator, but not by much; see [22] (Figure 8a–d). Comparisons between the Regression estimator and other error SD estimators for a simulated version of the Mt. Isa scene are shown in [22] (Figure 5a–c). They also demonstrate that the error variances for this scene do not satisfy Assumption 1. However, for simulated data, we can divide (“scale”) the data in each band by the known error SD of that band to produce data whose error SDs do satisfy Assumption 1. In addition, we know that for the scaled data, ${\sigma }^2=1$. We can then compute the eigenvalues for the scaled data. I call these the true-scaled eigenvalues.

Figure 1a–c plot the means +/−2 SDs for the noise eigenvalues among the true-scaled eigenvalues for ten simulations of each of the three exemplar scenes respectively, as well as the MP approximation to them, between $EID+1$ and d. For each of the ten simulations per scene, the signal component is the same. However, the errors vary, being Gaussian with band error variances given by the Regression estimators of them in the corresponding real scenes. The $ID$ and $EID$, as well as $d_{ϵ}$, for the three exemplar scenes are given in

Table 2. ID, EID and $d_{ϵ}$ for three exemplar simulated scenes.

Scene	ID	EID	${\mathit{d}}_{\mathit{ϵ}}$
Indian Pines	20	19	174
Cuprite	36	32	153
Mt. Isa	41	40	84

. Note that in each case, $EID<ID$ by a small amount. The reasons behind choosing these exemplar values of ID are given in [22] (Section II-B). The values of EID have not been chosen; they are a function of the simulated signal after ID has been chosen. I also plot the line $Y=1$ (the theoretical mean of the MP distribution after appropriate scale and offset adjustments) for reference.

Before discussing the adequacy of the MP approximation, it is worth explaining how the approximations in the plots relate to the theoretical results. First, the true-scaled noise eigenvalues need to be thought of as an empirical distribution function. Like a cdf, these normally increase. However, the noise eigenvalues are clearly decreasing. Let $F\left(w\right)$ denote the cdf of the MP($1,{\rho }_{ϵ}$) distribution, where

$${\rho }_{ϵ}\equiv d_{ϵ}/N=(d-EID)/N,$$

(7)

by (6). As mentioned earlier, $F\left(w\right)$ doesn’t have an analytic form, so we obtain a good approximation by numerically integrating (2) using Simpson’s rule at $d_{ϵ}$ equally spaced points between (and including) the endpoints, given by (3). Denote these points by $w_i,i=1,\dots ,d_{ϵ}$. These points lie along the Y axis. For the X axis, we need to plot $1-F\left(w_i\right),i=1,\dots ,d_{ϵ}$ (because the noise eigenvalues decrease rather than increase), with suitable offset and gain adjustments. Because $F\left(w\right)$ is a cdf, we must have $0\le 1-F\left(w\right)\le 1$. However, the X axis doesn’t satisfy this. We need to plot $EID+d_{ϵ}(1-F\left(w_i\right)),$ $i=1,\dots ,d_{ϵ}$ along the X axis to make the scaling correct.

For the Indian Pines and Cuprite scenes, the MP distribution approximates the eigenvalue means very well, with a little variation about them. For the Mt. Isa scene, the approximation is not quite so good for the largest noise eigenvalues because $d_{ϵ}$ (=84) is a lot smaller than it is for the other two scenes (174 and 153 respectively). It is however good for the smaller noise eigenvalues. Although the adequacy of the MP approximation will also depend to some extent on the signal component of any scene, these simulations suggest that $d>150$ and $N>$ 20,000 will usually allow these two distributions to provide reasonable approximations to the distribution of the true-scaled noise eigenvalues.

2.2.2. The Largest Noise Eigenvalue

In this section, I give some relevant results about the asymptotic behaviour of the largest noise eigenvalue under Assumptions 1 and 2. Let $l_1>l_2>\dots >l_d$ denote the eigenvalues.

Under Assumptions 1 and 2, certain mild moment conditions and when no signal is present, Geman [33] shows that

$$l_1\to {\sigma }^2{(1+\sqrt{\rho })}^2$$

(8)

almost surely as $N\to \infty$. Note that the right hand side of (8) is also the upper limit of the range of the (limiting) MP distribution, given as b in (3). So we expect that in large samples, $l_1<{\sigma }^2{(1+\sqrt{\rho })}^2$.

The extension of (8) when signal is present and EID = L is:

$$l_{L+1}\to {\sigma }^2{(1+\sqrt{{\rho }_{ϵ}})}^2,$$

(9)

where ${\rho }_{ϵ}$ is given by (7). I will call the right hand side of (9) the Geman limit, after the author of [33]. An obvious asymptotic estimator of EID is then:

$$RM{T}_G=max(k:l_k>{\sigma }^2{(1+\sqrt{(d-k)/N})}^2),$$

(10)

by (7). Somewhat surprisingly, this estimator does not appear to have been suggested before.

Several authors give the limiting distribution of $l_1$ when no signal is present. Specifically, following [34], Ref. [12] (Theorem 1) give the following result. Under Assumptions 1 and 2, assuming that the errors are Normally distributed and when no signal is present:

$$Pr(\frac{l_1/{\sigma }^2-{\mu }_{N,d}}{{\xi }_{N,d}}<s)\to H\left(s\right),$$

(11)

as $d,N\to \infty$ with $d/N\to \rho$, where

$${\mu }_{N,d}={\{{(1-1/2N)}^{\frac{1}{2}}+{(d/N-1/2N)}^{\frac{1}{2}}\}}^2,$$

(12)

$${\xi }_{N,d}={({\mu }_{N,d}/N)}^{\frac{1}{2}}{\{{(N-1/2)}^{-\frac{1}{2}}+{(d-1/2)}^{-\frac{1}{2}}\}}^{\frac{1}{3}},$$

(13)

and $H\left(s\right)$ is the cdf of the Tracy-Widom distribution of order 1, given in [34] (Section 1.3). The formulae for ${\mu }_{N,d}$ and ${\xi }_{N,d}$ given by [34] (Equations (1.3) and (1.4)) are slightly different to those above, given by [12] (Theorem 1), although asymptotically equivalent. However, I use (12) and (13) because they are also used by [11] when estimating the ID assuming that the error variances are unequal and unknown. I will further discuss the approach adopted by [11] shortly.

The limiting result (11) suggests the following RMT-based estimator of the EID:

$$RM{T}_{KN}=max(k:l_k>{\sigma }^2({\mu }_{N,d-k}+s\left(\alpha \right){\xi }_{N,d-k})),$$

(14)

where $s\left(\alpha \right)$ is chosen so that the test has a false alarm (Type I error) with asymptotic probability $\alpha$, i.e.,

$$H\left(s\right(\alpha \left)\right)=1-\alpha .$$

(15)

Unfortunately, $H\left(s\right)$ doesn’t have an explicit closed form expression. However, Ref. [12] (Equation (7) give the following approximate formula for $s\left(\alpha \right)$:

$$s\left(\alpha \right)\approx {(-3log\left(4\sqrt{\pi }\alpha \right)/2)}^{\frac{2}{3}},$$

(16)

which they assert is good when $\alpha \ll 1$. Both [11,12] use $\alpha =0.005$. I will use the same value in this paper.

The test (14) is also known as Roy’s largest root test [35].

Note that ${\mu }_{N,d}/{(1+\sqrt{d/N})}^2\to 1$ as $d,N\to \infty$ with $d/N\to \rho$, so that, provided N and d are large enough, the right hand side of the test (10) is less than the right hand side of the test (14). This is what happens for all the combinations of $N,d-k$ and $\alpha$ presented in this paper. Hence, because the eigenvalues are decreasing, for all the real and simulated data sets discussed in this paper, $RM{T}_{KN}\le RM{T}_G$.

2.2.3. The Difference between the Largest and Second Largest Noise Eigenvalues

Let ${\delta }_k=l_k-l_{k+1},k=1,\dots ,d-1$ denote the differences between successive eigenvalues. Passemier and Yao [13] propose the following ID estimator:

$$RM{T}_{PY}=max(k:{\delta }_k\ge c_{N}and{\delta }_{k+1}<c_N).$$

(17)

They show [13] (Theorem 3.1) that, under Assumptions 1 and 2, and provided that $d/N\to \rho ,c_N\to 0$ and $N^{\frac{2}{3}}{c}_N\to \infty ,RM{T}_{PY}\to EID$ almost surely as $N\to \infty$.

The authors tested various choices of $c_N$ and ultimately chose

$$c_N=4\sqrt{2log\left(log\right(N\left)\right)}(1+\sqrt{\rho }){(1+\sqrt{{\rho }^{-1}})}^{\frac{1}{3}}/N^{\frac{2}{3}}.$$

(18)

I will also use this value of $c_N$ in this paper.

As we shall see shortly, when Assumptions 1 and 2 hold, $RM{T}_{PY}$ is quite a good estimator of EID. However, as we shall also see, it is not robust to even small departures from this assumption. The “max” in (17) means that sometimes $RM{T}_{PY}$ chooses an estimate which is far too large. I will investigate an alternative estimator, which replaces “max” with “min”:

$$RM{T}_{PY2}=min(k:{\delta }_k\ge c_{N}and{\delta }_{k+1}<c_N).$$

(19)

2.3. Comparison of Different Id Estimators

In Section 2.3.1, I compare six ID estimators (including five based on various aspects of RMT theory) when the error variances are known. Simulations demonstrate that only three of these estimators are unbiased or minimally biased. So I exclude the other three estimators from further consideration. In Section 2.3.2, I discuss two estimators, introduced under the unrealistic assumption that the variances are equal but unknown. In Section 2.3.3, I discuss two estimators, which modify the two estimators in Section 2.3.2 to deal with the situation where the variances are unequal. I point out that the preprocessing method that they use does not make Assumption 1 hold, which is the fundamental reason for their bias.

2.3.1. ID Estimation When the Band Error Variances Are Known

In this section, I compare the ID estimators $RM{T}_G,RM{T}_{KN},RM{T}_{PY}$ and $RM{T}_{PY2}$, when the error variances are known. I also include two other ID estimators found to be the best among five other estimators by [22] (Section IV-A), called $NWHFC$ and $RM{T}_{CN}$. $NWHFC$ was one of three ID estimators proposed by [2]. The other two estimators, $HFC$ and $NSP$, do not work nearly as well as $NWHFC$ (see [22] (Figure 9a–d)) and so have been excluded from the comparison here. $NWHFC$ first divides (“scales”) each band by an estimator of its error SD and successively tests the equivalence of corresponding (scaled) eigenvalues of a scene with and without mean correction. The $NWHFC$ ID estimator is the number of corresponding eigenvalues which are significantly different from each other. The tests require a false alarm probability, $P_f$. In most papers, $P_f$ is set to ${10}^{-3},{10}^{-4}$ or ${10}^{-5}$. In [22] (Section IV-A) we chose the middle value ${10}^{-4}$. It produced ID estimates which were always too small. So in the comparison here, I will use ${10}^{-3}$, which will produce larger ID estimates. Because the error SDs are known, I will first divide each band by its error SD to preprocess $RM{T}_G,RM{T}_{KN},RM{T}_{PY},RM{T}_{PY2}$ and $NWHFC$.

$RM{T}_{CN}$ [11] does not do this. It first estimates the difference between corresponding eigenvalues of the data (signal plus noise) and the signal alone. This requires estimation of the band error variances (In the simulations discussed below, we will use the true error variances). It then uses the theory underlying $RM{T}_{KN}$ to produce an estimator of ID. However, its preprocessing does not involve division of each band by the (estimated or true) error SD, and hence as we shall see shortly, the critical Assumption 1 is not satisfied!

I have produced semi-realistic simulations of the three scenes mentioned above for a range of ID values: 17–29 for Indian Pines; 22–37 for Cuprite; and 25–45 for Mt. Isa. The reasons for choosing these particular ranges are given in [22] (Section II-B). As before, ten simulations have been generated for each scene/ID combination, with the same signal component, but different error components. Further details can be found in [21].

Figure 2a–c plot the mean +/−2 SDs for the six ID estimators (plus ID and EID) against the true ID for the Indian Pines, Cuprite and Mt. Isa scenes, respectively. A number of common results are apparent for the three scenes. First, EID = ID for smaller ID values, but becomes a little less than ID for larger values. Second $RM{T}_G,RM{T}_{KN}$ and $RM{T}_{PY}$ track EID quite well, with $RM{T}_G$ being the closest to EID, followed by $RM{T}_{KN}$ and then $RM{T}_{PY}$. Indeed the error bars for $RM{T}_G$ always include EID for the larger Cuprite and Mt. Isa scenes. However, for the the much smaller Indian Pines scene and larger ID values, the error bars for $RM{T}_G$ do not quite include EID. I speculate that this is primarily due to the small image size (N) and secondarily due to the decreasing pure noise dimension ($d_{ϵ}$) as EID increases.

For the smaller Indian Pines image, $RM{T}_{PY2}$ is quite similar to $RM{T}_{PY}$ for ID $\le 22$. However, for larger ID values, it is significantly smaller than $RM{T}_{PY}$, with the difference increasing as ID increases. It is also more variable for the larger ID values. For the larger Cuprite and Mt. Isa scenes, $RM{T}_{PY2}$ generally tracks $RM{T}_{PY}$ better. However, occasionally, its mean is much smaller than the corresponding mean of $RM{T}_{PY}$, and also much more variable (ID $=30$ for Cuprite, and ID $=39,43,44$ and 45 for Mt. Isa).

$RM{T}_{CN}$ and $NWHFC$ give much poorer estimates of EID (especially when it is larger) than the best estimators, the former because it does not satisfy Assumption 1 after preprocessing, and the latter because testing the statistical equivalence of corresponding scaled eigenvalues with and without mean correction is not nearly as powerful as RMT, when Assumption 1 is satisfied. Because, $RM{T}_{PY2},RM{T}_{CN}$ and $NWHFC$ perform more poorly when the error variances are known, I will exclude them from consideration when the error variances are unknown, and just focus on $RM{T}_G,RM{T}_{KN}$ and $RM{T}_{PY}$.

2.3.2. ID Estimation When the Band Error Variances Are Equal

Two papers [12,13] consider the performance of $RM{T}_{KN}$ and $RM{T}_{PY}$, respectively, when the band error variances are equal (i.e., Assumption 1 holds) but are unknown and must be estimated. This requires replacing ${\sigma }^2$ in (14) and (17), respectively, by an estimator of it. Both [12,13] use the same estimator. However, it varies with k:

$${\widehat{\sigma }}_k^2=\sum _{j=k+1}^d{l}_j/(d-k).$$

(20)

Under Assumption 1, this is the maximum likelihood estimator of ${\sigma }^2$ [36] (Equation (13b)).

Both [12,13] analyse the performance of $RM{T}_{KN}$ and $RM{T}_{PY}$, respectively, with the aid of simulations only. Because they do not analyse real world data, they are unaware that Assumption 1 is unrealistic for such data, especially hyperspectral remote sensing data. If one uses the best of the error variance estimators found in [22], the PMR estimator (which can be a little biased), to make the error variances approximately equal, and then use (20) to estimate ${\sigma }^2$ in (14), it can happen that the inequality in (14) is never satisfied. This happens for both the real and simulated Mt. Isa scenes. We will obtain an insight into why this is so in Section 2.4. I have not investigated whether the same happens to the inequalities in (17) when the PMR estimator is used to preprocess any of the real or simulated scenes.

2.3.3. ID Estimation When the Band Error Variances Are Unequal

Two other papers [11,14] both assume that the band error variances are (possibly) unequal, and estimate them. Cawse-Nicholson et al. [11] use a method based on finding homogeneous areas [37] to estimate them. Berman et al. [22] (Figures 3a, 4a, 5a and 6a) demonstrate that these estimators are far more biased than the PMR estimators. However, the more fundamental issue, mentioned above, is that their preprocessing does not make Assumption 1 hold, even approximately; see Figure 2a–c and [22] (Figure 10a–d). Error variance estimation just increases the bias of the ID estimates.

Halimi et al. [14] use the same preprocessing approach as [11]. They use an extension of the Regression method [25] to estimate a full error covariance matrix. This is known to be biased [26]. However, more fundamentally because it uses the same preprocessing as [11], it does not make Assumption 1 hold, and so suffers from similar problems.

2.4. Combining the Best Preprocessing and Id Estimation Methods

As mentioned in the Introduction, of the five error variance/SD estimators investigated by [22] (Section III), the one that consistently showed the smallest bias was the MR estimator [26]. However, for the real and simulated Mt. Isa data sets, the MR estimator is sometimes negative; see [22] (Figure 7). So [22] introduced a small modification, called the PMR estimator, to guarantee positivity. Figure 3a–c plot the mean +/−2 SDs for $RM{T}_G,RM{T}_{KN}$ and $RM{T}_{PY}$ (plus ID and EID) against the true ID for the simulated Indian Pines, Cuprite and Mt. Isa scenes, respectively, when the data have first been divided by the PMR estimators of the band error SDs. These should be compared with Figure 2a–c, which respectively show those ID estimators plus three others, when the data have been divided by the true band error SDs.

For Indian Pines, there is not much difference between Figure 2a and Figure 3a. When dividing the data by the PMR SD estimators, typically $RM{T}_G>RM{T}_{KN}>RM{T}_{PY}$. Note however that for ID $\le 20$, the mean of $RM{T}_G$ is a little positively biased, while the means of the other two estimators are a little negatively biased. For ID $>20$, the means of all three estimators are negatively biased. Things however are different for Cuprite and Mt. Isa. First, note that for both scenes the error bars for some values of $RM{T}_{PY}$ are very large. Indeed, for Cuprite, the means of $RM{T}_{PY}$ for the four ID values with very large error bars lie between 43 and 90, while for Mt. Isa, the means of $RM{T}_{PY}$ for all values of ID $>27$ lie between 47 and 121. We shall see why this is so shortly. For Cuprite and Mt. Isa, both $RM{T}_G$ and $RM{T}_{KN}$ are better behaved. However, for both scenes, their negative bias increases significantly as ID increases. This does not happen when the data have been divided by the true error SDs; compare Figure 2b,c with Figure 3b,c respectively.

To obtain a better understanding of the various behaviours of $RM{T}_G$, $RM{T}_{KN}$ and $RM{T}_{PY}$ when the data have been divided by the PMR estimators of the band error SDs, Figure 4a–c show the means (+/−2 SDs) of the tail eigenvalues after division by the true error SDs (in black), and the Regression (in red) and PMR (in green) estimators of them for ten simulations of each of the three exemplar scenes respectively. I will call the three sets of scaled eigenvalues in each plot the true-scaled, Regression-scaled and PMR-scaled eigenvalues respectively. As well as plotting the noise eigenvalues, I have included the last few signal eigenvalues before them, so that one can see the transition behaviour between the signal and noise eigenvalues. The true-scaled noise eigenvalues (in black) in Figure 4a–c are the same as the eigenvalues in Figure 1a–c respectively. The broken horizontal line in each plot is the Geman limit (the right hand side of (9) with ${\sigma }^2=1$), while the broken vertical line is $Y=EID+0.5$. For $RM{T}_G$ to give the correct estimate of EID, it is necessary (but not quite sufficient) that the first noise eigenvalue lies in the top left hand corner of the bottom right hand quadrant defined by these two lines. This happens 10, 9 and 8 (out of 10) times for the exemplar Indian Pines, Cuprite and Mt. Isa scenes respectively.

The first thing to note from the three figures is that, for all three scenes, the PMR-scaled noise eigenvalues are much closer to the true-scaled noise eigenvalues than the Regression-scaled noise eigenvalues are, demonstrating the value of the first order bias correction provided by the MR method [26]. For the Indian Pines scene, the PMR-scaled noise eigenvalues are slightly positively biased, which explains why $RM{T}_G$ is usually positively biased for this value of ID (=20); see Figure 3a. On the other hand, for the Cuprite and Mt. Isa scenes, the PMR-scaled noise eigenvalues are more significantly negatively biased, explaining why $RM{T}_G$ is negatively biased for these ID values (36 and 41 respectively); see Figure 3b,c, respectively.

A plausibility argument for the larger bias in the Cuprite and Mt. Isa scenes follows from theoretical and empirical arguments in [21] (Section II-C). These arguments suggest that, on average, the bias of the Regression estimator [25] is mainly a function of $M/d$. This value is 0.104, 0.195 and 0.331 for the Indian Pines, Cuprite and Mt. Isa simulated exemplar scenes respectively. The MR estimators [26] are linear combinations of the Regression estimators, which provide first order corrections to those estimators. Although the MR (and PMR) estimators significantly reduce the bias, the empirical evidence is that their average bias is also mainly a function of $M/d$. This translates to the average relative bias of the PMR-scaled noise eigenvalues; it also appears to be mainly a function of $M/d$.

Also note that the magnitude of the relative bias of the PMR-scaled noise eigenvalues for the exemplar Cuprite and Mt. Isa scenes (Figure 4b,c respectively) increases dramatically in the extreme tail. This explains the large error bars for $RM{T}_{PY}$ for certain ID values for these two scenes; see Figure 3b,c. Note that the rate of change of the PMR-scaled noise eigenvalues in the extreme tail is comparable to the rate of change of those eigenvalues just before the true ID in those figures. Hence, because the definition of $RM{T}_{PY}$ (17) is based on the last occurrence of a difference larger than $c_N$ followed by a difference smaller than $c_N$, there is a reasonable chance of this occurring in the extreme tail of the eigenvalues rather in the vicinity of the true ID value. It is for this reason that I investigated $RM{T}_{PY2}$ (19), which finds the first occurrence of the same event. However, this has its own problems, even when using the true-scaled eigenvalues; see Figure 2a–c.

The increasing magnitude of the relative bias of the PMR-scaled noise eigenvalues for the exemplar Mt. Isa scene (Figure 4c) is also the reason why the inequality in (14) is never satisfied for both the real and simulated Mt. Isa scenes, when (20) is used to estimate ${\sigma }^2$ in (14), even after the data have been scaled by the PMR estimates of the error SDs.

The bias in the PMR-scaled eigenvalues has less effect on $RM{T}_G$ and $RM{T}_{KN}$ than it does on $RM{T}_{PY}$, because they are based on the largest noise eigenvalue, which is the least biased of all the noise eigenvalues, as can be seen in Figure 4a–c. Nevertheless, both $RM{T}_G$ and $RM{T}_{KN}$ become increasingly biased as the ID increases. In the next section, I show how to reduce this bias further.

2.5. Further Reducing the Bias in $RM{T}_G$ and $RM{T}_{KN}$

In order to reduce the bias in $RM{T}_G$ and $RM{T}_{KN}$ further, it is worth examining more carefully the relative bias of the PMR-scaled noise eigenvalues. Figure 5a–c plot the means (+/−2 SDs) of the PMR-scaled tail eigenvalues divided by the corresponding true-scaled tail eigenvalues for the three exemplar scenes; a few signal eigenvalue ratios have again been included for comparison with the noise eigenvalue ratios. In each plot, a broken vertical red line has been included at $Y=EID+0.5$ to separate the signal eigenvalue ratios from the noise eigenvalue ratios. For the Indian Pines exemplar scene (with a smaller value of $M/d$), the means of the ratios are fairly constant. However for the Cuprite and Mt. Isa scenes, the ratio increases as the eigenvalue index increases, at first slowly but dramatically in the extreme tail. The basic idea for further reducing the bias is to obtain an initial estimate of the EID ($\widehat{L}$) using either $RM{T}_G$ or $RM{T}_{KN}$, and then to assume that the eigenvalue ratio changes linearly (including an offset) for the first few indices beyond the (estimated) ID. Note however that for the Cuprite and Mt. Isa exemplar scenes, $RM{T}_G$ and $RM{T}_{KN}$ are typically a little too small (see Figure 3b,c respectively), and the eigenvalue ratios just after $RM{T}_G$ and $RM{T}_{KN}$ are somewhat different to those after the true EID; see Figure 5b,c. So we need enough eigenvalues (say a proportion p) beyond the true EID to counteract those before the true EID when estimating the straight line needed to adjust the thresholds. Of course, we don’t know what the true-scaled eigenvalues are. However, they are well approximated by the MP(1, ${\rho }_{ϵ}$) distribution; see Figure 1a–c. As mentioned in the discussion of these figures, I noted that the X axis values are given by $EID+d_{ϵ}(1-F\left(w_i\right)),i=1,\dots ,d_{ϵ}$, where $d_{ϵ}=d-EID$, F is calculated via numerical integration of (2) and the $w_i,i=1,\dots ,d_{ϵ}$ are equally spaced points between the endpoints of the distribution (3). Of course, in the above calculation, we replace $EID$ by $\widehat{L}$. The X axis values are typically not equally spaced. However, they need to be to correspond to the eigenvalue indices. I have just linearly interpolated the values of $F\left(w_i\right)$ to make them equally spaced. Also note that, because we will be adjusting the Y values, we only need to regress the PMR-scaled eigenvalues on the interpolated values of $1-F\left(w\right)$, rather than on the interpolated values of $EID+d_{ϵ}(1-F\left(w\right))$. Once a proportion p of the PMR-scaled eigenvalues beyond $\widehat{L}$ have been fitted to the corresponding points on $1-F\left(w\right)$, they can be readjusted to better fit the theoretical distribution. The details of the adjusted algorithm are given in Algorithm 1.

Algorithm 1 Adjusted EID estimation algorithm

Divide each band by the PMR-estimator of its SD. Denote the (decreasing) PMR-scaled eigenvalues by ${\widehat{l}}_i,i=1,\dots ,d.$ Obtain an initial estimate of EID ($\widehat{L}$), either $RM{T}_G$ (10) or $RM{T}_{KN}$ (14) with ${\sigma }^2=1.$ Linearly fit ${\widehat{l}}_i,i=\widehat{L}+1,\dots ,\widehat{L}+p(d-\widehat{L})$ (rounded to the nearest integer) to the corresponding points of the linearly interpolated values of $1-F\left(w\right)$, where $F\left(w\right)$ is the cdf of the MP(1, $(d-\widehat{L})/N$)    distribution. Let A and B denote the offset and gain of the linear regression. The final estimate of EID is given by applying either $RM{T}_G$ (10) or $RM{T}_{KN}$ (14) with ${\sigma }^2=1$ to $({\widehat{l}}_i-A)/B,i=1,\dots ,d.$

Figure 6a–c plot the mean +/−2 SDs for the original $RM{T}_G$ and $RM{T}_{KN}$ estimates plus adjusted versions of them using Algorithm 1 against the true ID for the simulated Indian Pines, Cuprite and Mt. Isa scenes respectively, when the data have first been divided by the PMR estimators of the band error SDs. The values of p used are $p=0.10$ (with the estimators denoted by $RM{T}_G\left(10\right)$ and $RM{T}_{KN}\left(10\right)$ respectively) and $p=0.50$ ($RM{T}_G\left(50\right)$ and $RM{T}_{KN}\left(50\right)$ respectively). As before, ID and EID have also been included. The values for $RM{T}_G$ and $RM{T}_{KN}$ are the same as those in Figure 3.

Overall, $RM{T}_G\left(50\right)$ appears to perform best, followed by $RM{T}_{KN}\left(50\right)$. For the Indian Pines data, for ID $\le 20$, whereas the mean of $RM{T}_G$ is a little positively biased, the mean of $RM{T}_G\left(50\right)$ is a little negatively biased. However, its error bars do include EID. For larger values of ID, there is not much difference between $RM{T}_G$ and $RM{T}_G\left(50\right)$. However, for the highest ID values considered, the error bars just miss EID. On the other hand, for the larger Cuprite and Mt. Isa scenes, the means of both $RM{T}_G$ and $RM{T}_G\left(50\right)$ are very close to ID (= EID) for smaller values. However, for larger ID, the bias of the mean of $RM{T}_G\left(50\right)$ is less than that of $RM{T}_G$.

Nevertheless, even though $RM{T}_G\left(50\right)$ is less biased than $RM{T}_G$ is for larger ID values for these two scenes, the error bars are a long way from including EID. To understand why this is so, in Figure 7, I plot true-scaled eigenvalues 29 to 100 for a single simulation of the exemplar Cuprite scene for which ID = 36 and EID = 32. For this scene, $RM{T}_G=RM{T}_{KN}=29$. I also plot the corresponding adjusted PMR-scaled noise eigenvalues with $\widehat{L}=29$ (the estimate provided by either $RM{T}_G$ or $RM{T}_{KN}$) and $\widehat{L}=32$ (the true EID value). I have also drawn horizontal lines corresponding to the Geman limit when EID = 29 and EID = 32 respectively. These values are not very different (1.0450 and 1.0446 respectively). True-scaled eigenvalues 29 to 32 (but not 33) lie above both these thresholds, so that, if we knew the true error variances $RM{T}_G=32$, the correct value. In this case, $RM{T}_{KN}=31$. If we adjust the PMR-scaled eigenvalues using $\widehat{L}=32$ (with $p=0.5$), we see that the adjusted eigenvalues follow the true-scaled eigenvalues quite well from index 34 onwards. However, for indices below 34, the approximation is not so good, and becomes worse as the index becomes smaller. In this case, adjusted eigenvalues 29 and 30 lie above both thresholds (while 31 does not), so that $RM{T}_G\left(50\right)=30$, while $RM{T}_{KN}\left(50\right)=30$ also. However, in reality, $\widehat{L}=29$. When we use this value to adjust the PMR-scaled eigenvalues (again with $p=0.5$) the fit is a little worse, with the fitted values lying a little below those using $\widehat{L}=32$. The difference however is not enough to change the values of the two estimators. The behaviour that we see in Figure 7 is fairly typical of the other simulations, and explains why the improvement in the ID estimates is generally small when the adjustment described in Algorithm 1 is applied; see Figure 6a–c.

I am unaware of an RMT-based theory that deals with the bias of the PMR-estimators of the error variances, and the fact that the bias is variable; see [22] (Figure 8a–d). The more likely route to reducing the bias in the ID estimators probably lies in further reducing the bias in error variance estimation.

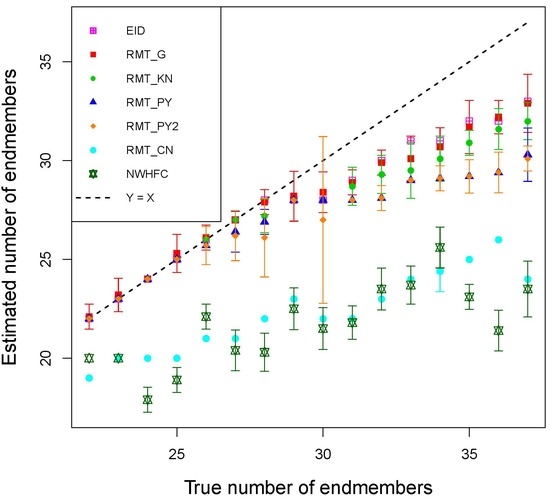
3. Results

In

Table 3. Various ID estimates for the three real data sets.

Estimator	Indian Pines	Cuprite	Mt. Isa
$HySime$	11	16	17
$NWHFC$	19, 19, 18	29, 28, 24	32, 27, 25
$RM{T}_{CN}$	20	33	61
$RM{T}_{PY}$	24	180	119
$RM{T}_{PY2}$	24	39	56
$RM{T}_G$	56	46	65
$RM{T}_{KN}$	54	46	65
Adj. $RM{T}_G$	53, 52, 52	46, 48, 48	65, 65, 65
Adj. $RM{T}_{KN}$	49, 46, 46	45, 47, 48	63, 63, 63

, I give various ID estimators for the three real scenes. These include the estimators compared and introduced previously ($NWHFC,RM{T}_{CN},RM{T}_{PY},RM{T}_{PY2},RM{T}_G$ and $RM{T}_{KN}$), as well as the adjusted versions of $RM{T}_G$ and $RM{T}_{KN}$ introduced in Section 2.5. I have also included $HySime$, because the paper in which it was introduced [4] is widely cited. It was excluded from comparison in this paper, because in simulations reported in [22] it always significantly underestimated EID, even when the true error variances were known. For all estimators except $HySime$, the PMR estimators are used to preprocess the data before applying the ID estimator. For $HySime$, the Regression estimators (which are intrinsic to the method) are used. Among the other estimators, all except $RM{T}_{CN}$ preprocess the data by dividing/scaling each band by the PMR error SD estimator of that band. $RM{T}_{CN}$ uses a different preprocessing procedure; see [11] (Algorithm 1). For $NWHFC$, I give the values for the usual three false alarm probabilities ${10}^{-3},{10}^{-4}$ and ${10}^{-5}$. The adjusted $RM{T}_G$ and $RM{T}_{KN}$ estimators are given for $p=0.1,0.3$ and $0.5$.

The ranges of true ID values used in the simulations summarised in Figure 2a–c, Figure 3a–c and Figure 6a–c were largely based on the assumption that, for each of the real scenes, the true EID value lies in the range covered by the estimates $HFC,NWHFC$ and $RM{T}_{CN}$ for those scenes; $NSP$ was excluded because it always seemed too large, while $HySime$ was excluded because it usually seemed too small. The $HySime$ estimates are indeed the smallest ID estimates for each of the three real scenes given in Table 3, followed by the $NWHFC$ estimates and then $RM{T}_{CN}$, except for Mt. Isa, where it is very much larger. For Indian Pines, $RM{T}_{PY}$ and $RM{T}_{PY2}$ are a little larger again. However, for Cuprite and Mt. Isa, $RM{T}_{PY}$ is much larger (in each case a little smaller than d, the number of bands). This behaviour was also observed in the simulated versions of these two data sets (see Figure 3b,c) and is explained by the behaviour of the PMR-scaled eigenvalues in the extreme tail (see Figure 4b,c). $RM{T}_{PY2}$ is robust to this behaviour, but can be highly variable, even when the error variances are known; see Figure 2a–c.

Ignoring the anomalous behaviour of $RM{T}_{PY}$ for the real Cuprite and Mt. Isa scenes, $RM{T}_G$ and $RM{T}_{KN}$ (and their adjusted versions) are considerably larger than the other estimators. In the next subsection, I discuss possible reasons why this might be so.

4. Discussion

I can think of six possible explanations for why $RM{T}_G$ and $RM{T}_{KN}$ are much larger than the other ID estimators; see Table 3. I will now discuss each of these in turn.

4.1. Endmember Variability

The first possibility is that the $RM{T}_G$ and $RM{T}_{KN}$ ID estimates are indeed close to the true EID values. After all, they were found to be unbiased or slightly biased (for EID) when the true error variances are known (see Figure 2a–c), with a slightly greater bias when PMR is used to estimate the true error variances (see Figure 3a–c). In the latter case, $RM{T}_G$ and $RM{T}_{KN}$ underestimate EID! So if these values are close to the true EID values, how does one explain such large values?

Clark et al. [38] analysed the composition of the full 1995 AVIRIS Cuprite scene; in this paper, I have analysed a 1997 subscene. Apart from the fact that ours is a subscene, one expects the identifiable minerals from the two scenes to be similar. They used their Tetracorder software (which is based on feature identification rather than a mixture model) to identify various minerals from this scene. If one counts the number of mineral “classes” in their two maps (see their Figure 9a,b), there are 40 distinct colours in the two legends, which is a little less than 46, the $RM{T}_G$ and $RM{T}_{KN}$ estimates for the subscene. One of the labels associated with individual colours in the legends includes terms such as “amorphous and other iron oxides, hydroxides” (which suggests a single colour covering several minerals which may be spectrally distinct). Four types of hematite, three types of K-alunite, two types of Na-alunite and three types of muscovite are also listed. These last four groupings are an example of what is sometimes called “endmember variability” [39,40,41], which describes the spectral variability of materials with the same label. There are several causes of such variability including variable grain sizes (in the case of minerals) and chemical substitutions. If one ignores endmember variability, the number of minerals with distinct labels in the legends decreases significantly, and is closer to ID estimates found by many of the other ID estimation methods. This suggests that $RM{T}_G$ and $RM{T}_{KN}$ may be more sensitive to endmember variability than the other methods.

The Indian Pines scene is an agricultural scene with 16 “groundtruth” classes (http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes), with labels such as “Grass-pasture”, “Grass-trees” and “Grass-pasture-mowed”. These are also likely to contain different types of grasses and trees, some of which may be spectrally distinct, and so endmember variability is almost certainly present in the scene. Also, the map at this website showing the spatial variability of the 16 classes has significant unclassified sections. The materials present in them will add to the true ID of the scene.

The Mt. Isa scene is also dominated by minerals, and so the endmember variability issues relevant to the Cuprite scene will also apply to the Mt. Isa scene.

Given the presence of endmember variability, it is perhaps not so surprising that, when one assumes the linear mixture model (1) with uncorrelated errors, the number of spectrally distinct materials is as high as is suggested by $RM{T}_G$ and $RM{T}_{KN}$ in Table 3 for all three scenes.

4.2. Deterministic Errors

Many hyperspectral scenes contain deterministic errors. Often they can be incorporated into model (1); see [22] (Equation (16)) which includes a single horizontal stripe within this model. Such deterministic errors will then contribute to the ID of the scene. The Mt.Isa scene contains obvious deterministic errors, caused by an orthorectification process; see [22] (Figure 1a). The Indian Pines scene contains more subtle deterministic errors; see [21] (Figure 6a). Deterministic errors are not obvious in the Cuprite scene.

Ref. [22] (Section V-D) discuss the issue of deterministic errors in some detail, with a particular focus on striping noise. Their analysis highlights the difficulty of estimating the contribution to the ID of deterministic errors such as striping. None of the numerous papers on “destriping” (some of which are referenced during that discussion) use ID as a measure of the adequacy of the proposed destriping method. This area requires further research with the aid of simulations. The simulation methodology proposed in [21] and used in this paper can be readily adapted to include deterministic errors.

4.3. Spectrally Correlated Errors

Spectrally correlated errors are actually quite common in hyperspectral images. Often these occur because parts of the spectra have been smoothed, either because they are locally noisy or because the sensors actually consist of several spectrometers whose wavelength ranges overlap and the overlapping spectra measured at each pixel need to be joined into a single spectrum that appears continuous and locally smooth. For instance, AVIRIS and HyMap are both built on four spectrometers [23] (p. 231), [24] (p. 39). An error correlation matrix estimation method that I will shortly describe shows distinct peaks in the correlation structure at about the join points of the AVIRIS spectrometers for both the real Indian Pines and Cuprite scenes (both measured by AVIRIS). The method also shows distinct peaks in the correlation structure for the Mt. Isa scene (measured by HyMap), but not near the join points of the HyMap spectrometers. I don’t know why this is so.

In theory, dealing with spectrally correlated errors is straightforward. Let ${\mathsf{\Sigma }}_T$ and ${\mathsf{\Sigma }}_{ϵ}$ denote the theoretical data and error covariance matrices respectively. We just need to whiten the data by simultaneously diagonalising ${\mathsf{\Sigma }}_T$ and ${\mathsf{\Sigma }}_{ϵ}$. The estimated error covariance matrix of the transformed data is then the identity matrix, and all the random matrix theory in Section 2.2 applies. The transformation just described is the Minimum Noise Fraction (MNF) transform [42]. However, these matrices need to be estimated. The observed data covariance matrix is the obvious (and unbiased) estimator of ${\mathsf{\Sigma }}_T$. When the MNF transform is used, ${\mathsf{\Sigma }}_{ϵ}$ is usually estimated using spatial information, rather than spectral information. Using spatial information leads to much less accurate estimators of ${\mathsf{\Sigma }}_{ϵ}$ than using spectral information does; see [22] (Figures 3b, 4b, 5b and 6b).

Mahmood et al. [26] extend their MR method to deal with data with spectrally correlated errors. Details will not be given here. However, although it looks promising, it has three shortcomings. First, one needs to assume which of the errors have non-zero covariances. In what follows, I will use the time series term “lag” to describe the distance between two bands, and the parameter $max.lag$ will be used to give the maximum lag between bands with correlated errors. $max.lag=0$ corresponds to spectrally uncorrelated errors. In work that will be published elsewhere, I have applied the extension of the MR method to the three real data sets assuming that $max.lag=0,1,2,3,4$ and 5, used the estimated error covariance matrix, ${\widehat{\mathsf{\Sigma }}}_{ϵ}$, to whiten the data, and then calculated $RM{T}_G$ and $RM{T}_{KN}$.

For the whitening procedure to work, it is necessary that ${\widehat{\mathsf{\Sigma }}}_{ϵ}$ be positive definite. Unfortunately, for the real Mt. Isa data set, this matrix is never positive definite for any of the values of $max.lag$ investigated. I have fixed this second shortcoming using a modification of the PMR method, which is applicable to the eigenvalues of the MNF transform. Applying this modification to the three real data sets demonstrates that (i) for the real Indian Pines and Mt. Isa data sets, $RM{T}_G$ and $RM{T}_{KN}$ decrease as $max.lag$ increases, (ii) for the real Cuprite scene, both $RM{T}_G$ and $RM{T}_{KN}$ increase initially to $max.lag=2$ and then gradually decrease, (iii) the percentage relative difference between the minimum and maximum values of $RM{T}_G$ over the six values of $max.lag$ are 29%, 25% and 12% for the real Indian Pines, Cuprite and Mt. Isa scenes respectively (the percentages for $RM{T}_{KN}$ are similar). A more detailed description of the work summarised in this paragraph will be given elsewhere.

Given the significant percentage variability in the estimates of $RM{T}_G$ and $RM{T}_{KN}$ for the three scenes as $max.lag$ varies, it becomes important to develop a test of the true value of $max.lag$. In Section 2.4, I have demonstrated that, when the errors are uncorrelated, the small relative bias of the PMR method induces a bias in $RM{T}_G$ and $RM{T}_{KN}$. It is likely that the extension of the PMR method to the case of correlated errors will also be biased (although I have yet to confirm this with the aid of simulatons). This is the third (potential) shortcoming. The existence of this bias will make it difficult to develop an estimate of the true value of $max.lag$ with good theoretical properties.

4.4. Spatially Correlated Errors

Spatially correlated errors are common in images. There have been some papers published on the estimation of error variances in the presence of such errors (e.g., [43,44]). However, to my knowledge, nobody has investigated the impact of spatially correlated errors on ID estimation. A suitable model would probably involve an extension of (1) to include nearby pixels, and the cross-correlations between both signal and noise across pixels. An approach generalising the Regression method [25] to include nearby pixels is the most obvious starting point. This has been used to estimate the noise directly (which is different from estimating the second order statistics of the noise) by [27] and others. However, its properties would need to be carefully analysed under the suggested extension of (1). Ideally, an extension of the MR method [26] could also be proposed under such a model.

4.5. Signal-Dependent Errors

In reality, the instrumental noise in many hyperspectral sensors is better modelled as a linear combination of two types of noise: signal-independent (SI) noise, which typically uses the same model as has been used in this paper (i.e., uncorrelated Gaussian noise with a possibly different variance in each band); and signal-dependent (SD) noise, which is typically modelled as Poisson noise [45,46,47]. These three papers use different methods to estimate the parameters of the SI and SD noise components in each band. However, regardless of the parameter estimation method used, it is not clear that RMT can be applied to data with a combination of both these types of noise. This is because, unlike for spectrally and/or spatially correlated errors, the error structure varies from pixel to pixel, and hence the concept of an error covariance matrix for the full image (which can somehow be converted to the identity matrix) does not even exist!

4.6. Non-Linear Mixing

There is also likely to be some non-linear mixing in most hyperspectral images. The linear model (1) can be thought of as a Taylor series approximation to a more accurate non-linear model, and hence the ID of the linear model is likely to be an overestimate of the number of “spectrally distinct” materials in the image. Note that, in the model (1), ID = M. This is also the number of parameters in this linear model. This provides a natural way to define the ID in non-linear models. There have been a number of non-linear mixture models published in recent years [48,49,50,51,52,53]. There needs to be further research on (i) how to estimate the ID for these models, and (ii) the advantages and disadvantages of using them compared with the basic linear mixture model (1). In particular, ID estimation for non-linear mixture models is likely to be difficult, because as far as I am aware, there is no comparable theory to random matrix theory for non-linear models.

5. Summary and Conclusions

Random matrix theory provides a powerful and elegant set of theoretical tools relevant to ID estimation. I have shown that when Assumptions 1 and 2 hold (or when the band error variances are known), $RM{T}_G$, $RM{T}_{KN}$ and $RM{T}_{PY}$ track EID quite well, with $RM{T}_G$ being the closest to EID, followed by $RM{T}_{KN}$ and then $RM{T}_{PY}$; see Figure 2a–c. Most of my focus in this paper has been on violations of Assumption 1, i.e., that the band error variances are equal. When we use the best estimator of the error variances that we know of, the PMR estimator, to whiten the data before calculating these ID estimators, we observe that both $RM{T}_G$ and $RM{T}_{KN}$ are somewhat biased, especially for larger ID values, and that $RM{T}_{PY}$ performs much more poorly; see Figure 3a–c. The biases in $RM{T}_G$ and $RM{T}_{KN}$ are due to the small bias in the PMR estimator. The explanation of the much poorer performance of $RM{T}_{PY}$ is revealed in Figure 4a–c. These figures show how, when estimated error variances are used, the bias is much greater in the extreme tail eigenvalues, which has a bigger impact on $RM{T}_{PY}$ than on either $RM{T}_G$ and $RM{T}_{KN}$, which both seek to identify the largest noise eigenvalue. Figure 4a–c also suggest a method (Algorithm 1) for reducing the bias in $RM{T}_G$ and $RM{T}_{KN}$.

All the above results are based on simulated data. When $RM{T}_G$ and $RM{T}_{KN}$ are applied to real data, they are much larger than most of the more widely used ID estimates; see Table 3. Possible reasons for this are discussed, including endmember variability, deterministic errors, spectrally correlated errors, spatially correlated errors, signal-dependent errors and non-linear mixing.

The research presented in this paper has also raised the following research questions: (i) can the bias in the MR method be reduced, so that the bias in $RM{T}_G$ and $RM{T}_{KN}$ is also reduced? (ii) how does one estimate the ID of deterministic errors? (iii) how can the “extent” of spectrally correlated errors (effectively $max.lag$) be reliably estimated? (iv) how can spatially correlated errors be reliably estimated? (v) how can the ID be reliably estimated in the presence of signal-dependent errors, (vi) how can the ID of a non-linear model be reliably estimated?

Finally, it is worth mentioning that the three scenes that have been simulated in this paper have been chosen because each displays different characteristics relevant to ID estimation. The Cuprite scene was chosen because, at first glance, it had few (if any) artefacts. However, it does appear to have spectral correlation (due to the interpolation and smoothing of spectra from its four spectrometers). The Indian Pines scene was chosen because it is much smaller than the other two scenes, and yet the (asymptotic) random theory is still applicable to it; see Figure 1a. It was also chosen because, unlike the other two scenes, it exhibits subtle spatially correlated errors. It is unclear whether these errors are deterministic or stochastic. The Mt. Isa scene was chosen because the MR estimators of it and its simulated versions produce error covariance estimates which are not positive definite, and so require modification.