Assimilation of Satellite Salinity for Modelling the Congo River Plume
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.2. Observations
2.3. Assimilation Scheme
2.4. Data Assimilation Experiments
3. Results
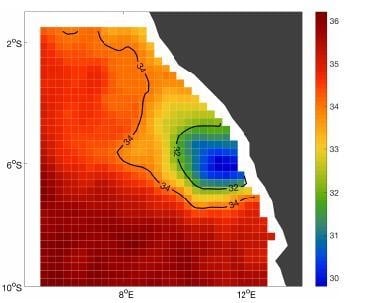
3.1. Assimilation Analysis
3.2. Forecast
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dagg, M.; Benner, R.; Lohrenz, S.; Lawrence, D. Transformation of dissolved and particulate materials on continental shelves influenced by large rivers: Plume processes. Cont. Shelf Res. 2004, 24, 833–858. [Google Scholar] [CrossRef]
- Chen, C.T.A.; Zhai, W.; Dai, M. Riverine input and air-sea CO2 exchanges near the Changjiang (Yangtze River) Estuary: Status quo and implication on possible future changes in metabolic status. Cont. Shelf Res. 2008, 28, 1476–1482. [Google Scholar] [CrossRef]
- Kang, Y.; Pan, D.; Bai, Y.; He, X.; Chen, X.; Chen, C.T.A.; Wang, D. Areas of the global major river plumes. Acta Oceanol. Sin. 2013, 32, 79–88. [Google Scholar] [CrossRef]
- Hopkins, J.; Lucas, M.; Dufau, C.; Sutton, M.; Stum, J.; Lauret, O.; Channelliere, C. Detection and variability of the Congo River plume from satellite derived sea surface temperature, salinity, ocean colour and sea level. Remote. Sens. Environ. 2013, 139, 365–385. [Google Scholar] [CrossRef]
- Braga, E.S.; Andrié, C.; Bourlès, B.; Vangriesheim, A.; Baurand, F.; Chuchla, R. Congo River signature and deep circulation in the eastern Guinea Basin. Deep-Sea Res. Part I Oceanogr. Res. Pap. 2004, 51, 1057–1073. [Google Scholar] [CrossRef]
- Higgins, H.W.; Mackey, D.J.; Clementson, L. Phytoplankton distribution in the Bismarck Sea north of Papua New Guinea: The effect of the Sepik River outflow. Deep-Sea Res. Part I Oceanogr. Res. Pap. 2006, 53, 1845–1863. [Google Scholar] [CrossRef]
- Kouame, K.; Yapo, O.; Mambo, V.; Seka, A.; Tidou, A.; Houenou, P. Physicochemical Characterization of the Waters of the Coastal Rivers and the Lagoonal System of Cote d‘Ivoire. J. Appl. Sci. 2009, 9, 1517–1523. [Google Scholar] [CrossRef]
- Yankovsky, A.E.; Chapman, D.C. A simple theory for the fate of buoyant coastal discharges. J. Phys. Oceanogr. 1997, 27, 1386–1401. [Google Scholar] [CrossRef] [Green Version]
- Eisma, D.; van Bennekom, A.J. The Zaire river and estuary and the Zaire outflow in the Atlantic Ocean. Neth. J. Sea Res. 1978, 12, 255–272. [Google Scholar] [CrossRef]
- Denamiel, C.; Budgell, W.P.; Toumi, R. The congo river plume: Impact of the forcing on the far-field and near-field dynamics. J. Geophys. Res. Ocean. 2013, 118, 964–989. [Google Scholar] [CrossRef]
- Signorini, S.R.; Murtugudde, R.G.; McClain, C.R.; Christian, J.R.; Picaut, J.; Busalacchi, A.J. Biological and physical signatures in the tropical and subtropical Atlantic. J. Geophys. Res. Ocean. 1999, 104, 18367–18382. [Google Scholar] [CrossRef] [Green Version]
- Vic, C.; Berger, H.; Tréguier, A.M.; Couvelard, X. Dynamics of an Equatorial River Plume: Theory and Numerical Experiments Applied to the Congo Plume Case. J. Phys. Oceanogr. 2014, 44, 980–994. [Google Scholar] [CrossRef] [Green Version]
- Palma, E.D.; Matano, R.P. An idealized study of near equatorial river plumes. J. Geophys. Res. Ocean. 2017, 122, 3599–3620. [Google Scholar] [CrossRef]
- White, R.H.; Toumi, R. River flow and ocean temperatures: The Congo River. J. Geophys. Res. Ocean. 2014, 119, 2501–2517. [Google Scholar] [CrossRef]
- Bars, Y.L.; Vallaeys, V.; Deleersnijder, É.; Hanert, E.; Carrere, L.; Channelière, C. Unstructured-mesh modeling of the Congo river-to-sea continuum. Ocean. Dyn. 2016, 66, 589–603. [Google Scholar] [CrossRef]
- Liu, Y.; MacCready, P.; Hickey, B.M.; Dever, E.P.; Kosro, P.M.; Banas, N.S. Evaluation of a coastal ocean circulation model for the Columbia River plume in summer 2004. J. Geophys. Res. Ocean. 2009, 114, C00B04. [Google Scholar] [CrossRef] [Green Version]
- Lahoz, W.; Khattatov, B.; Ménard, R. Data assimilation and information. In Data Assimilation: Making Sense of Observations, 1st ed.; Lahoz, W., Khattatov, B., Menard, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Chapter 1; pp. 3–12. [Google Scholar]
- Lu, Z.; Cheng, L.; Zhu, J.; Lin, R. The complementary role of SMOS sea surface salinity observations for estimating global ocean salinity state. J. Geophys. Res. Ocean. 2016, 121, 3672–3691. [Google Scholar] [CrossRef]
- Köhl, A.; Sena Martins, M.; Stammer, D. Impact of assimilating surface salinity from SMOS on ocean circulation estimates. J. Geophys. Res. Ocean. 2014, 119, 5449–5464. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote. Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Mu, Z.; Zhang, W.; Wang, P.; Wang, H.; Yang, X. Assimilation of SMOS sea surface salinity in the regional ocean model for South China Sea. Remote. Sens. 2019, 11, 919. [Google Scholar] [CrossRef] [Green Version]
- Moore, A.M.; Arango, H.G.; Broquet, G.; Edwards, C.; Veneziani, M.; Powell, B.; Foley, D.; Doyle, J.D.; Costa, D.; Robinson, P. The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems. Part III—Observation impact and observation sensitivity in the California Current System. Prog. Oceanogr. 2011, 91, 74–94. [Google Scholar] [CrossRef]
- Phillipson, L.; Toumi, R. Impact of data assimilation on ocean current forecasts in the Angola Basin. Ocean. Model. 2017, 114, 45–58. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Vorosmarty, C.; Fekete, B.M.; Tucker, B. Global River Discharge, 1807–1991, V. 1.1 (RivDIS); Oak Ridge Natl. Lab. Distrib. Active Arch. Cent.: Oak Ridge, TN, USA, 1998. [Google Scholar]
- Meybeck, M.; Ragu, A. GEMS-GLORI World River Discharge Database; Lab. de Gologie Appl., Univ. Pierre et Marie Curie: Paris, France, 2012. [Google Scholar]
- Alsdorf, D.; Beighley, E.; Laraque, A.; Lee, H.; Tshimanga, R.; O’Loughlin, F.; Mahé, G.; Dinga, B.; Moukandi, G.; Spencer, R.G.M. Opportunities for hydrologic research in the Congo Basin. Rev. Geophys. 2016, 54, 378–409. [Google Scholar] [CrossRef] [Green Version]
- Jackson, B.; Nicholson, S.E.; Klotter, D. Mesoscale Convective Systems over Western Equatorial Africa and Their Relationship to Large-Scale Circulation. Mon. Weather. Rev. 2009, 137, 1272–1294. [Google Scholar] [CrossRef]
- Phillipson, L. Ocean Data Assimilation in the Angola Basin. Ph.D. Thesis, Imperial College London, London, UK, 2018. [Google Scholar]
- SMOS-BEC Team. Quality Report: Validation of Debiased Non-Bayesian BEC advanced Sea Surface Salinity Products; Technical Report; Barcelona Expert Centre: Barcelona, Spain, 2017. [Google Scholar]
- Willis, J.K. Interannual variability in upper ocean heat content, temperature, and thermosteric expansion on global scales. J. Geophys. Res. 2004, 109, C12036. [Google Scholar] [CrossRef] [Green Version]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Ocean. 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Weaver, A.T.; Deltel, C.; Machu, E.; Ricci, S.; Daget, N. A multivariate balance operator for variational ocean data assimilation. Q. J. R. Meteorol. Soc. 2006, 131, 3605–3625. [Google Scholar] [CrossRef] [Green Version]
- Moore, A.M.; Edwards, C.A.; Fiechter, J.; Drake, P.; Neveu, E.; Arango, H.G.; Gürol, S.; Weaver, A.T. A 4D-var analysis system for the california current: A prototype for an operational regional ocean data assimilation system. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. II); Springer: Berlin/Heidelberg, Germany, 2013; pp. 345–366. [Google Scholar]
- Lumpkin, R.; Johnson, G.C. Global ocean surface velocities from drifters: Mean, variance, El Niño–Southern Oscillation response, and seasonal cycle. J. Geophys. Res. Ocean. 2013, 118, 2992–3006. [Google Scholar] [CrossRef]
- Phillipson, L.M.; Toumi, R. The Crossover Time as an Evaluation of Ocean Models Against Persistence. Geophys. Res. Lett. 2018, 45, 250–257. [Google Scholar] [CrossRef] [Green Version]
- Fukumori, I.; Raghunath, R.; Fu, L.L.; Chao, Y. Assimilation of TOPEX/Poseidon altimeter data into a global ocean circulation model: How good are the results? J. Geophys. Res. Ocean. 1999, 104, 25647–25665. [Google Scholar] [CrossRef]
- Dorofeev, V.L.; Korotaev, G.K. Assimilation of the data of satellite altimetry in an eddy-resolving model of circulation of the Black Sea. Phys. Oceanogr. 2004, 14, 42–56. [Google Scholar] [CrossRef]
- Dombrowsky, E.; Bertino, L.; Brassington, G.; Chassignet, E.; Davidson, F.; Hurlburt, H.; Kamachi, M.; Lee, T.; Martin, M.; Mei, S.; et al. GODAE Systems in Operation. Oceanography. 2009, 22, 80–95. [Google Scholar] [CrossRef] [Green Version]
- Moore, A.M.; Arango, H.G.; Broquet, G.; Edwards, C.; Veneziani, M.; Powell, B.; Foley, D.; Doyle, J.D.; Costa, D.; Robinson, P. The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems. Part II—Performance and application to the California Current System. Prog. Oceanogr. 2011, 91, 50–73. [Google Scholar] [CrossRef]
- Da Rocha Fragoso, M.; de Carvalho, G.V.; Soares, F.L.M.; Faller, D.G.; de Freitas Assad, L.P.; Toste, R.; Sancho, L.M.B.; Passos, E.N.; Böck, C.S.; Reis, B.; et al. A 4D-variational ocean data assimilation application for Santos Basin, Brazil. Ocean. Dyn. 2016, 66, 419–434. [Google Scholar] [CrossRef]
- Desroziers, G.; Camino, J.T.; Berre, L. 4DEnVar: Link with 4D state formulation of variational assimilation and different possible implementations. Q. J. R. Meteorol. Soc. 2014, 140, 2097–2110. [Google Scholar] [CrossRef]
- Font, J.; Boutin, J.; Reul, N.; Spurgeon, P.; Ballabrera-Poy, J.; Chuprin, A.; Gabarró, C.; Gourrion, J.; Guimbard, S.; Hénocq, C.; et al. SMOS first data analysis for sea surface salinity determination. Int. J. Remote. Sens. 2013, 34, 3654–3670. [Google Scholar] [CrossRef]










| (a) January | (b) April | ||||
|---|---|---|---|---|---|
| Exp. Name | RMSE (PSU) | R | Exp. Name | RMSE (PSU) | R |
| CNTRL | CNTRL | ||||
| SSH | SSH | ||||
| SMOS | SMOS | ||||
| SMOS SSH | SMOS SSH | ||||
| (c) July | (d) August | ||||
| Exp. Name | RMSE (PSU) | R | Exp. Name | RMSE (PSU) | R |
| CNTRL | CNTRL | ||||
| SSH | SSH | ||||
| SMOS | SMOS | ||||
| SMOS SSH | SMOS SSH | ||||
| Exp. Name | Area | COM Dist. | Angle | Inside Salinity | Mean % |
|---|---|---|---|---|---|
| MAE (km) | MAE (km) | MAE () | MAE (PSU) | Improv. | |
| January | |||||
| CNTRL | 27,454 | 78 | 2.0 | 2.53 | - |
| SSH | 74,515 | 75 | 1.2 | 2.37 | −30% |
| SMOS | 8084 | 6 | 1.9 | 1.06 | 56% |
| SMOS SSH | 8754 | 5 | 1.1 | 0.95 | 68% |
| April | |||||
| CNTRL | 144,409 | 13 | 10.1 | 1.78 | - |
| SSH | 160,850 | 9 | 11.5 | 1.78 | 1% |
| SMOS | 5291 | 11 | 0.4 | 0.54 | 68% |
| SMOS SSH | 7936 | 9 | 0.7 | 0.55 | 72% |
| July | |||||
| CNTRL | 18,654 | 39 | 7.6 | 3.59 | - |
| SSH | 10,582 | 36 | 13.2 | 3.26 | −4% |
| SMOS | 7425 | 13 | 3.8 | 2.42 | 52% |
| SMOS SSH | 6154 | 12 | 2.4 | 2.53 | 58% |
| August | |||||
| CNTRL | 26,897 | 118 | 39.9 | 4.99 | - |
| SSH | 23,309 | 73 | 6.4 | 4.37 | 37% |
| SMOS | 4053 | 7 | 0.9 | 2.22 | 83% |
| SMOS SSH | 4882 | 3 | 0.9 | 2.73 | 81% |
| Whole Domain | Inside Plume | |||||||
|---|---|---|---|---|---|---|---|---|
| No. of Argo Float Samples | ||||||||
| Jan | Apr | Jul | Aug | Jan | Apr | Jul | Aug | |
| 38 | 17 | 22 | 24 | 0 | 3 | 4 | 3 | |
| Analysis Exp. Name | MAE (PSU) | MAE (PSU) | ||||||
| CNTRL | − | |||||||
| SSH | − | |||||||
| SMOS | − | |||||||
| SMOS SSH | − | |||||||
| SMOS DATA | − | |||||||
| Exp. Name | Area | COM Dist. | Angle | Inside Salinity | Mean % |
|---|---|---|---|---|---|
| MAE (km) | MAE (km) | MAE () | MAE (PSU) | Improv. | |
| January | |||||
| CNTRL | 140,152 | 33 | 14.7 | 2.05 | - |
| SSH | 209,978 | 12 | 12.1 | 1.79 | 11% |
| SMOS | 19,801 | 16 | 0.7 | 1.28 | 68% |
| SMOS SSH | 5893 | 8 | 1.9 | 1.15 | 75% |
| SMOS PERSIST | 9174 | 14 | 1.1 | 0.08 | 85% |
| April | |||||
| CNTRL | 264,010 | 77 | 9.7 | 1.01 | - |
| SSH | 246,378 | 70 | 8.9 | 1.12 | 3% |
| SMOS | 43,054 | 36 | 3.0 | 0.60 | 62% |
| SMOS SSH | 31,586 | 43 | 1.2 | 1.01 | 55% |
| SMOS PERSIST | 11,433 | 5 | 0.4 | 0.04 | 95% |
| July | |||||
| CNTRL | 9764 | 86 | 9.3 | 2.93 | - |
| SSH | 8867 | 83 | 18.0 | 3.28 | −23% |
| SMOS | 9685 | 72 | 16.4 | 3.04 | −16% |
| SMOS SSH | 8061 | 65 | 15.2 | 3.29 | −9% |
| SMOS PERSIST | 2305 | 3 | 1.6 | 0.02 | 90% |
| August | |||||
| CNTRL | 18,121 | 85 | 20.2 | 2.94 | - |
| SSH | 5291 | 52 | 7.9 | 3.09 | 41% |
| SMOS | 7482 | 109 | 41.0 | 3.75 | −25% |
| SMOS SSH | 21,754 | 30 | 4.4 | 4.15 | 21% |
| SMOS PERSIST | 7403 | 8 | 1.0 | 0.09 | 85% |
| Whole Domain | Inside Plume | |||||||
|---|---|---|---|---|---|---|---|---|
| No. of Float Samples | ||||||||
| Jan | Apr | Jul | Aug | Jan | Apr | Jul | Aug | |
| 31 | 21 | 25 | 27 | 5 | 4 | 2 | 1 | |
| Forecast Exp. Name | MAE (PSU) | MAE (PSU) | ||||||
| CNTRL | ||||||||
| SSH | ||||||||
| SMOS | ||||||||
| SMOS SSH | ||||||||
| SMOS PERSIST | ||||||||
| SMOS DATA | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phillipson, L.; Toumi, R. Assimilation of Satellite Salinity for Modelling the Congo River Plume. Remote Sens. 2020, 12, 11. https://doi.org/10.3390/rs12010011
Phillipson L, Toumi R. Assimilation of Satellite Salinity for Modelling the Congo River Plume. Remote Sensing. 2020; 12(1):11. https://doi.org/10.3390/rs12010011
Chicago/Turabian StylePhillipson, Luke, and Ralf Toumi. 2020. "Assimilation of Satellite Salinity for Modelling the Congo River Plume" Remote Sensing 12, no. 1: 11. https://doi.org/10.3390/rs12010011
APA StylePhillipson, L., & Toumi, R. (2020). Assimilation of Satellite Salinity for Modelling the Congo River Plume. Remote Sensing, 12(1), 11. https://doi.org/10.3390/rs12010011