Simulation Study of Moon-Based InSAR Observation for Solid Earth Tides
Abstract
:1. Introduction
2. Model and Simulation Methods
2.1. SET Model and Lunar View Displacement Distribution
2.1.1. Tidal Displacement Model
- The latitude dependence and slight inter-band variations of Love number caused by the earth oblateness and the Coriolis force.
- The strong frequency dependence in the diurnal band and some other frequency dependence, owing to diurnal free oscillation resonance and inelastic mantle.
- The centrifugal force perturbation influenced by the inelastic mantle causing the Love number to lag behind the imaginary part of the TGP.
2.1.2. Lunar View Displacement Distribution
2.2. Simulation of Deformation Information
3. Simulation Results and Analyses
3.1. Tidal Displacement Characteristic
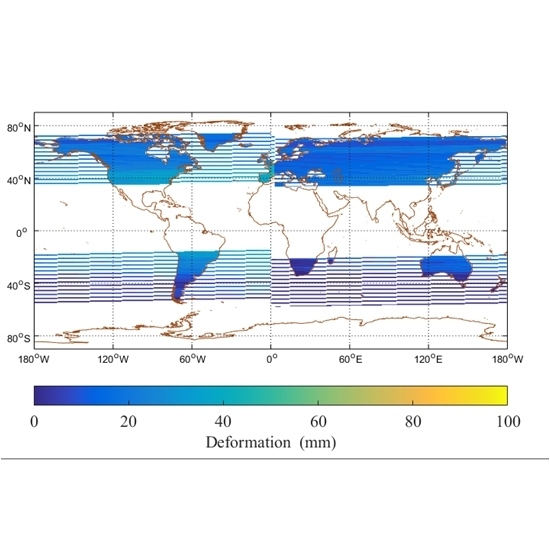
- The extreme point of the solid tidal displacement always appears near the lunar subpoint. Combined with the fact that there is always one side of the moon facing the earth, this feature makes the moon-based platform always have more abundant displacement information, which is not available on other artificial space satellite platforms. Although the difference calculation in interferometry can eliminate some of the displacement information, the change of the lunar subpoint in the cross-track direction ensures the existence of the deformation. As far as we know, the SET deformation information from lunar platform is most significant when compared with the low orbit platform and the geosynchronous orbit platform.
- It is difficult to observe the negative part of the SET displacement from the lunar view, and the displacement distribution decreases symmetrically from the extreme point to the surrounding area. We counted all time points with a maximum displacement of more than 300 mm, and found that 80% of them were concentrated in the time points corresponding to the middle and high lunar declination (7–21°).
- The displacement distribution is constantly changing, and always exhibits some periodicity. Additionally, its periodic rule will gradually weaken with the increase of periodicity length. For example, the diurnal changes within the same month are more regular than those in different months. If the temporal baseline of interference is too short, it may reduce the deformation information due to the similar displacement states. On the contrary, if the temporal baseline is too long, other types of deformation may produce significant noise. There is a need to balance the two situations and to select the ideal temporal baseline. This characteristic makes the temporal resolution advantage of the lunar platform play an important role, its shortest temporal baseline of approximately one day allows us to make flexible choices.
3.2. Interferometry Mode and Observation Geometry
3.2.1. Interferometry Mode
3.2.2. Observation Geometry
- In the whole period, the side-looking observation (the squint angle is 0) always has abundant SET information and is more recommended. If the lag effect of the tidal displacement on the TPG response is considered, backward-looking observation will be more appropriate (the antenna pointing to the east of the subpoint was defined as the backward-looking observation).
- When using side-looking observation, the observable range and tidal displacement are the largest. However, a blind area exists, which is approximately 9° north and south of the lunar subpoint. The squint angle is limited by the FOV, ranging from 0 to 1°. Different squint angle can reduce the blind area to some extent.
3.3. Observation Effect under Three Signal Bandwidths
3.3.1. Selection of Master Image
3.3.2. Deformation Information in EICs
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, J.Y. The Fundamentals of Geophysics; Surveying and Mapping Press: Beijing, China, 2001. [Google Scholar]
- Melchior, P. The Tides of Planet Earth, 2nd ed.; Pergamon: Oxford, UK, 1983. [Google Scholar]
- Goodkind, J.M. The superconducting gravimeter. Rev. Sci. Instrum. 1999, 70, 4131–4152. [Google Scholar] [CrossRef] [Green Version]
- Fang, J. The Solid Earth’s Tides; Science Press: Beijing, China, 1984. [Google Scholar]
- Zhang, G.; Xu, J.; Wang, X. International trends and progress of solid tide observation and research. J. Seismol. Res. 2004, 27, 104–107. [Google Scholar]
- Nige, T.P.; Matt, A.K.; Mike, P.S. GPS height time series: Short-period origins of spurious long-period signals. J. Geophys. Res. Solid Earth 2007, 112, B02402. [Google Scholar]
- Watson, C.; Tregoning, P.; Coleman, R. Impact of solid Earth tide models on GPS coordinate and tropospheric time series. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Montiguarnieri, A.; Prati, C.; Rocca, F.; Massonet, D. InSAR principles-guidelines for SAR interferometry processing and interpretation. J. Financ. Stab. 2007, 10, 156–162. [Google Scholar]
- Wright, T.J.; Parsons, B.; England, P.C.; Fielding, E.J. InSAR Observations of Low Slip Rates on the Major Faults of Western Tibet. Science 2004, 305, 236–239. [Google Scholar] [CrossRef] [Green Version]
- Delacourt, C.; Briole, P.; Achache, J.A. Tropospheric corrections of SAR interferograms with strong topography. Application to Etna. Geophys. Res. Lett. 1998, 25, 2849–2852. [Google Scholar] [CrossRef]
- Lu, Z.; Wicks, C.; Power, J.A.; Dzurisin, D. Ground deformation associated with the March 1996 earthquake swarm at Akutan volcano, Alaska, revealed by satellite radar interferometry. J. Geophys. Res. 2000, 105, 21483–21495. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.Y.; Zhang, Q.; Ding, X.L.; Lu, Z.; Yang, C.S.; Qi, X.M. Monitoring of land subsidence and ground fissures in Xian, China 2005-2006: Mapped by SAR interferometry. Environ. Geol. 2009, 58, 1533–1540. [Google Scholar] [CrossRef]
- Stevens, N.F.; Wadge, G.; Williams, C.A.; Morley, J.G.; Muller, J.P.; Murray, J.B. Surface movements of emplaced lava flows measured by synthetic aperture radar interferometry. J. Geophys. Res. 2001, 106, 11293–11313. [Google Scholar] [CrossRef]
- Hao, J.; Wu, T.; Wu, X.; Hu, G.; Zou, D.; Zhu, X.; Lin, Z.; Li, R.; Xie, C.; Ni, J.; et al. Investigation of a Small Landslide in the Qinghai-Tibet Plateau by InSAR and Absolute Deformation Model. Remote. Sens. 2019, 11, 2126. [Google Scholar] [CrossRef] [Green Version]
- Ramsey, E.; Lu, Z.; Rangoonwala, A.; Rykhus, R. Multiple Baseline Radar Interferometry Applied to Coastal Land Cover Classification and Change Analyses. GIScience Remote. Sens. 2006, 43, 283–309. [Google Scholar] [CrossRef] [Green Version]
- Zebker, H.A.; Werner, C.L.; Rosen, P.; Hensley, S. Accuracy of Topographic Maps Derived from ERS-1 Interferometric Radar. IEEE Trans. Geosci. Remote. Sens. 1993, 32, 823–836. [Google Scholar] [CrossRef] [Green Version]
- Williams, C.A.; Wadge, G. An accurate and efficient method for including the effects of topography in three dimensional elastic models of ground deformation with applications to radar interferometry. J. Geophys. Res. 2000, 105, 8103–8120. [Google Scholar] [CrossRef]
- Carnec, C.; Fabriol, H. Monitoring and modeling land subsidence at the Cerro Prieto geothermal field, Baja California, Mexico, using SAR interferometry. Geophys. Res. Lett. 1999, 26, 1211–1214. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, G.; Shan, X.; Gong, W.; Zhang, Y.; Li, Y. Co-Seismic Deformation and Fault Slip Model of the 2017 Mw 7.3 Darbandikhan, Iran–Iraq Earthquake Inferred from D-InSAR Measurements. Remote. Sens. 2019, 11, 2521. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2011, 514, 1–13. [Google Scholar] [CrossRef]
- Qiao, S.; Sun, F.; Zhu, X.; Li, J.; Cong, M. Application of GPS/VLBI/SLR/InSAR Combination in Geodynamics. J. Geod. Geodyn. 2004, 24, 92–97. [Google Scholar]
- Farolfi, G.; Ventisette, C.D. Monitoring the Earth’s ground surface movements using satellite observations-Geodynamics of the Italian peninsula determined by using GNSS networks. In Proceedings of the IEEE International Workshop on Metrology for Aerospace, Florence, Italy, 22–23 June 2016. [Google Scholar]
- Colesanti, C.; Ferretti, A.; Prati, C. Monitoring landslides and tectonic motions with the Permanent Scatterers Technique. Eng. Geol. 2003, 68, 3–14. [Google Scholar] [CrossRef]
- Bruno, D.; Hobbs, S.; Ottavianelli, G. Geosynchronous synthetic aperture radar: Concept design, properties and possible applications. Acta Astronaut. 2006, 59, 149–156. [Google Scholar] [CrossRef]
- Bruno, D.; Hobbs, S.E. Radar Imaging from Geosynchronous Orbit: Temporal Decorrelation Aspects. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2924–2929. [Google Scholar] [CrossRef]
- Crawford, I.A. Back to the Moon: The scientific rationale for resuming lunar surface exploration. Planet. Space Sci. 2012, 74, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Racca, G.D.; Foing, B.H.; Coradini, M. Smart-1: The First Time of Europe to the Moon; Wandering in the Earth–Moon Space. Earth-Moon Relationships. 2001, pp. 379–390. Available online: https://link.springer.com/chapter/10.1007/978-94-010-0800-6_32 (accessed on 1 November 2019).
- Zheng, Y.; Ouyang, Z.; Li, C.; Liu, J.; Zou, Y. China’s lunar exploration program: Present and future. Planet. Space Sci. 2003, 56, 881–886. [Google Scholar] [CrossRef]
- Fornaro, G.; Franceschetti, G.; Lombardini, F.; Mori, A.; Calamia, M. Potentials and limitations of Moon-Borne SAR imaging. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3009–3019. [Google Scholar] [CrossRef]
- Guo, H.D.; Liu, G.; Ding, Y.X. Moon-based Earth observation: Scientific concept and potential applications. Int. J. Digit. Earth. 2017, 11, 546–557. [Google Scholar] [CrossRef]
- Dehant, V.; Defraigne, P.; Wahr, J.M. Tides for a convective Earth. J. Geophys. Res. 1999, 104, 1035–1058. [Google Scholar] [CrossRef]
- IERS. IERS Technical Note. 2003 N0.32. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/TechnicalNotes.html (accessed on 27 December 2019).
- Xu, H. Solid Earth Tides; Hubei Science & Technology Press: Wuhan, China, 2010. [Google Scholar]
- Hartmann, T.; Wenzel, H.G. The HW95 tidal potential catalogue. Geophys. Res. Lett. 1995, 22, 3553–3556. [Google Scholar] [CrossRef]
- Xi, Q.W. The precision of the development of the tidal generating potential and some explanatory notes. Chin. J. Geophys. 1989, 2, 182–194. [Google Scholar]
- Hartmann, T.; Wenzel, H.G. The harmonic development of the Earth tide generating potential due to the direct effect of the planets. Geophys. Res. Lett. 1994, 21, 1991–1993. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The Planetary and Lunar Ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep. 2014, 42, 1–81. [Google Scholar]
- Ren, Y.; Guo, H.; Liu, G.; Ye, H. Simulation Study of Geometric Characteristics and Coverage for Moon-Based Earth Observation in the Electro-Optical Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 2431–2440. [Google Scholar] [CrossRef]
- Xia, Y. Synthetic Aperture Radar Interferometry; Springer: Berlin, Heidelberg, 2010. [Google Scholar]
- Zhang, F.; Ma, D.B.; Pei, H.N. Analysis of the Elements of Baseline Estimation of Interferometric SAR. Remote. Sens. Inf. 2005, 3, 7–9. [Google Scholar]
- Meyer, F.J.; Sandwell, D.T. SAR interferometry at Venus for topography and change detection. Planet. Space Sci. 2012, 73, 130–144. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y. Moonborne Earth Observation Synthetic Aperture Radar and Its Application in Global Change. Ph.D. Thesis, Graduate School of Chinese Academy of Sciences, Beijing, China, 10 July 2014. [Google Scholar]
- Guo, H.D.; Ding, Y.X.; Liu, G.; Zhang, D.W.; Fu, W.X.; Zhang, L. Conceptual study of lunar-based SAR for global change monitoring. Sci. China Earth Sci. 2014, 57, 1771–1779. [Google Scholar] [CrossRef]













| Factor | Error |
|---|---|
| Axial Precession | |
| Nutation | |
| Polar Wandering | |
| Free Nutation | |
| Position of Observation Station |
| Parameter (unit) | Value Range |
|---|---|
| Wavelength (cm) | 24 |
| Antenna Height (m) | 57 |
| Incident Angles (°) | 10–66 |
| Swath Width (km) | 1680–2802 |
| Signal Bandwidth (MHz) | 100 |
| Antenna Length (m) | 198–837 |
| 100 MHz | 200 MHz | 300 MHz | |
|---|---|---|---|
| Wavelength | 24 cm | 24 cm | 24 cm |
| Number of EICs | 13 | 26 | 33 |
| Spatial coverage | 27.80% | 44.50% | 51.60% |
| Deformation span | 8.8 cm | 14.2 cm | 19.1 cm |
| Distance beam broadening | 0.24° | 0.24° | 0.24° |
| Deformation span in swath | 4.0 cm | 7.1 cm | 9.4 cm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Ji, C.; Luo, L.; Wang, X. Simulation Study of Moon-Based InSAR Observation for Solid Earth Tides. Remote Sens. 2020, 12, 123. https://doi.org/10.3390/rs12010123
Wu K, Ji C, Luo L, Wang X. Simulation Study of Moon-Based InSAR Observation for Solid Earth Tides. Remote Sensing. 2020; 12(1):123. https://doi.org/10.3390/rs12010123
Chicago/Turabian StyleWu, Kai, Ce Ji, Lei Luo, and Xinyuan Wang. 2020. "Simulation Study of Moon-Based InSAR Observation for Solid Earth Tides" Remote Sensing 12, no. 1: 123. https://doi.org/10.3390/rs12010123
APA StyleWu, K., Ji, C., Luo, L., & Wang, X. (2020). Simulation Study of Moon-Based InSAR Observation for Solid Earth Tides. Remote Sensing, 12(1), 123. https://doi.org/10.3390/rs12010123