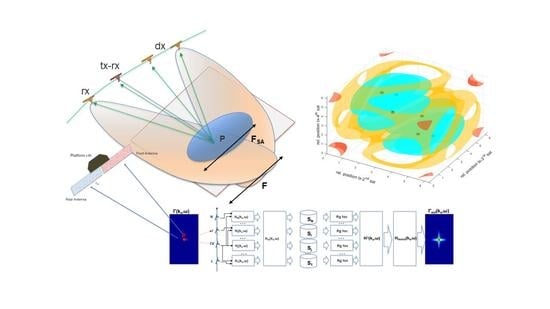
Along-Track Multistatic Synthetic Aperture Radar Formations of Minisatellites
Abstract
:1. Introduction
- A 2D frequency domain spectrum reconstruction method. The effects of noise and bad-conditioned matrix inversion are mitigated by means of a Wiener inversion, similarly to the Minimum Mean Squared Error (MMSE) in [13,14], and considered an optimum compromise between matched and ML filters. The reconstruction in frequency domain is used to account for range migration, as demonstrated also in [16].
- Two practical methods to mitigate the degradation of system performance due to the loss of position control: a dynamic tuning of PRF and the split of the antenna. Both of the methods that can act together aim at modifying the phase centers towards optimal positions.
- A systematical study of the degradation in phase shift and volume decorrelation, as a consequence of a realistic non zero across-track baseline, leading to the estimation of a critical tube width for the formation to avoid recombination problems.
2. SIMO SAR Formation
2.1. Design Bounds
2.2. The Model of the Received Signal
2.3. The Model in the Frequency Domain
3. Reconstruction of the Scene
3.1. Matrix Discrete Formulation
3.2. Recombination
3.3. Focusing of Equivalent Monostatic SAR
4. Control of Sensor Position
4.1. Relation between Formation Distance, PRF, and System Performance
4.2. Mitigation of System Performance Degradation
4.2.1. Tuning the PRF
4.2.2. Twin Antenna
- Use both rear and front parts, as there were 2 N receivers,
- Use a proper combination of rear or front that assures the best recombination scheme.
4.2.3. System Sensibility
5. System Limitations
5.1. Across-Track Baseline Effects
5.2. Tomographic Formations
6. Conclusions
7. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Probabilistic Approach to Matrix Inversion


References
- What is Space 4.0? Available online: http://www.esa.int/About_Us/Ministerial_Council_2016/What_is_space_4.0 (accessed on 28 December 2019).
- Yuen, B.; Sima, M. Low Cost Radiation Hardened Software and Hardware Implementation for CubeSats. Arb. Rev. 2018, 9, 46–62. [Google Scholar] [CrossRef]
- Currie, A.; Brown, M.A. Wide-swath SAR. IEE Proc. F-Radar Signal Process. 1992, 139, 122–135. [Google Scholar] [CrossRef]
- Younis, M.; Fischer, C.; Wiesbeck, W. Digital Beamforming in SAR Systems. Geosci. Remote Sens. IEEE Trans. 2003, 41, 1735–1739. [Google Scholar] [CrossRef]
- Mittermayer, J.; Runge, H. Conceptual studies for exploiting the TerraSAR-X dual receiving antenna. Geosci. Remote Sens. Symp. 2003, 3, 2140–2142. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR Signal Reconstruction from Nonuniform Displaced Phase Center Sampling. Geosci. Remote Sens. Lett. IEEE 2004, 1, 260–264. [Google Scholar] [CrossRef] [Green Version]
- Gebert, N.; Krieger, G.; Moreira, A. Digital Beamforming on Receive: Techniques and Optimization Strategies for High-Resolution Wide-Swath SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef] [Green Version]
- Gebert, N.; Krieger, G.; Moreira, A. Multichannel Azimuth Processing in ScanSAR and TOPS Mode Operation. Geosci. Remote Sens. IEEE Trans. 2010, 48, 2994–2998. [Google Scholar] [CrossRef] [Green Version]
- Aguttes, J.P. The SAR train concept: Required antenna area distributed over N smaller satellites, increase of performance by N. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; IEEE Cat. No.03CH37477. Volume 1, pp. 542–544. [Google Scholar] [CrossRef]
- Burns, R.; McLaughlin, C.A.; Leitner, J.; Martin, M. TechSat 21: Formation design, control, and simulation. In Proceedings of the 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 25 March 2000; (Cat. No.00TH8484). Volume 7, pp. 19–25. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I.; Klare, J.; Gierull, C.H. MIMO SAR Processing for Multichannel High-Resolution Wide-Swath Radars. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5034–5055. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Su, T.; Bao, Z. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 82–86. [Google Scholar] [CrossRef]
- Sikaneta, I.; Gierull, C.H.; Cerutti-Maori, D. Optimum Signal Processing for Multichannel SAR: With Application to High-Resolution Wide-Swath Imaging. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6095–6109. [Google Scholar] [CrossRef]
- Goodman, N.; Sih Chung, L.; Rajakrishna, D.; Stiles, J. Processing of Multiple-Receiver Spaceborne Arrays for Wide-Area SAR. Geosci. Remote Sens. IEEE Trans. 2002, 40, 841–852. [Google Scholar] [CrossRef]
- Cheng, P.; Wan, J.; Xin, Q.; Wang, Z.; He, M.; Nian, Y. An Improved Azimuth Reconstruction Method for Multichannel SAR Using Vandermonde Matrix. IEEE Geosci. Remote Sens. Lett. 2017, 14, 67–71. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Klare, J.; Sikaneta, I.; Gierull, C. Signal Reconstruction with Range Migration Correction for High-Resolution Wide-Swath SAR Systems. In Proceedings of the 10th European Conference on Synthetic Aperture Radar, EUSAR 2014, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Sakar, N.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Reigber, A.; Moreira, A. Analysis of Geometrical Approximations in Signal Reconstruction Methods for Multistatic SAR Constellations with Large Along-Track Baseline. IEEE Geosci. Remote Sens. Lett. 2018, 15, 892–896. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. SAR signal reconstruction from non-uniform displaced phase centre sampling. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2004, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1763–1766. [Google Scholar] [CrossRef] [Green Version]
- McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley Series in Remote Sensing; Wiley-Interscience: Hoboken, NJ, USA, 1991. [Google Scholar]
- D’Aria, D.; Monti Guarnieri, A. High-Resolution Spaceborne SAR Focusing by SVD-Stolt. IEEE Geosci. Remote Sens. Lett. 2007, 4, 639–643. [Google Scholar] [CrossRef] [Green Version]
- D’Aria, D.; Guarnieri, A.M.; Rocca, F. Focusing bistatic synthetic aperture radar using dip move out. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1362–1376. [Google Scholar] [CrossRef]
- Kraus, T.; Krieger, G.; Gerhard, K.; Moreira, A.; Bachmann, M. Addressing the Terrain Topography in Distributed SAR Imaging. In Proceedings of the IET International Conference on Radar Systems (Radar), Toulon, France, 23–27 September 2019. [Google Scholar]
- Bamler, R. A comparison of range-Doppler and wavenumber domain SAR focusing algorithms. IEEE Trans. Geosci. Remote Sens. 1992, 30, 706–713. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti Guarnieri, A.; Prati, C.; Rocca, F.; Massonnet, D. SAR Principles: Guidelines for SAR Interferometry Processing and Interpretation; Technical Report; ESA: Paris, France, 2017. [Google Scholar]
- Gatelli, F.; Monti Guamieri, A.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The wavenumber shift in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–865. [Google Scholar] [CrossRef] [Green Version]
- Fornaro, G.; Guarnieri, A.M. Minimum mean square error space-varying filtering of interferometric SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 11–21. [Google Scholar] [CrossRef]
- Bamler, R.; Just, D. Phase statistics and decorrelation in SAR interferograms. In Proceedings of the IGARSS ’93-IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; Volume 3, pp. 980–984. [Google Scholar] [CrossRef]
- Comon, P.; Jutten, C. Handbook of Blind Source Separation; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Peral, E.; Wye, L.; Lee, S.; Tanelli, S.; Rahmat-Samii, Y.; Horst, S.; Hoffman, J.; Yun, S.; Imken, T.; Hawkins, D. Radar Technologies for Earth Remote Sensing From CubeSat Platforms. Proc. IEEE 2018, 106, 404–418. [Google Scholar] [CrossRef]
- Marchenko, V.A.; Pastur, L.A. Distribution of eigenvalues for some sets of random matrices. Mat. Sb. (N.S.) 1967, 72, 507–536. [Google Scholar]










| Optimiz | PRF [Hz] | Cond Numb | Gain [dB] | Peak Power [dB] | 1s Ambig [dB] | Az Resol [m] | PSLR [dB] | 2D ISLR [dB] |
|---|---|---|---|---|---|---|---|---|
| 650 | 77.94 | 10.63 | 16.05 | 1.30 | 1.882 | −17.81 | −9.47 | |
| 1337.62 | 49.46 | 11.40 | 14.48 | −58.33 | 1.321 | −36.21 | −10.02 | |
| 650 | 1.93 | 14.24 | 15.57 | −27.61 | 1.778 | −16.46 | −9.03 | |
| 1337.62 | 4.19 | 15.02 | 13.44 | −69.52 | 1.118 | −30.42 | −10.14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guccione, P.; Monti Guarnieri, A.; Rocca, F.; Giudici, D.; Gebert, N. Along-Track Multistatic Synthetic Aperture Radar Formations of Minisatellites. Remote Sens. 2020, 12, 124. https://doi.org/10.3390/rs12010124
Guccione P, Monti Guarnieri A, Rocca F, Giudici D, Gebert N. Along-Track Multistatic Synthetic Aperture Radar Formations of Minisatellites. Remote Sensing. 2020; 12(1):124. https://doi.org/10.3390/rs12010124
Chicago/Turabian StyleGuccione, Pietro, Andrea Monti Guarnieri, Fabio Rocca, Davide Giudici, and Nico Gebert. 2020. "Along-Track Multistatic Synthetic Aperture Radar Formations of Minisatellites" Remote Sensing 12, no. 1: 124. https://doi.org/10.3390/rs12010124
APA StyleGuccione, P., Monti Guarnieri, A., Rocca, F., Giudici, D., & Gebert, N. (2020). Along-Track Multistatic Synthetic Aperture Radar Formations of Minisatellites. Remote Sensing, 12(1), 124. https://doi.org/10.3390/rs12010124