A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation
Abstract
:1. Introduction
2. Large-Scene Deceptive Jamming Method Based on TDFS-TS
2.1. Principles of Deceptive Jamming against SAR
2.2. TDFS-TS Algorithm
2.2.1. Deceptive Jamming Based on TDFS
2.2.2. Jamming Signal Analysis
2.2.3. Template Segmentation
2.2.4. Correction Algorithm in Squint Mode
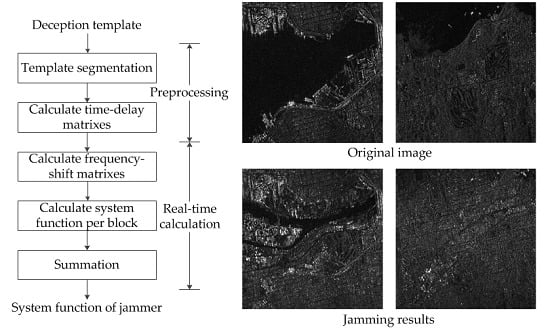
2.3. TDFS-TS Algorithm Procedure
- Kinematic parameters of the SAR platform, including motion trajectory, motion velocity , etc. The motion trajectory information is used to establish the jamming coordinate system and determine , the shortest distance between the jammer and SAR;
- Antenna parameters, including the squint angle , synthetic aperture length , etc.;
- Signal parameters, including the carrier frequency , bandwidth , PRI, etc.
3. Simulation Results
3.1. Fake Point Scatters Case
3.2. General Deceptive Scene Case
3.3. Computational Complexity Analysis
4. Discussion
4.1. Imaging Quality
- The imaging quality of the jamming signal in the range dimension depends on the azimuth position of the false scatter ;
- The distortion of the azimuth profile depends on both the range and the azimuth position of the false scatter;
- These distortions become severe as the distance between the fake scatter and the block center increases.
4.2. Computational Efficiency
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Walter, W.G. Synthetic Aperture Radar and Electronic Warfare; Artech House: Boston, MA, USA, 1993; pp. 25–39. [Google Scholar]
- Condley, C.J. Some system considerations for electronic countermeasures to synthetic aperture radar. In Proceedings of the IEE Colloquium on Electronic Warfare Systems, London, UK, 14 January 1991. [Google Scholar]
- Dumper, K.; Cooper, P.S.; Wons, A.F.; Condley, C.J.; Tully, P. Spaceborne synthetic aperture radar and noise jamming. In Proceedings of the 1997 Radar Edinburgh International Conference, Edinburgh, UK, 14–16 October 1997; pp. 411–414. [Google Scholar]
- Fouts, D.J.; Pace, P.E.; Karow, C.; Ekestorm, S.R.T. A single-chirp false target radar image generator for countering wideband imaging radars. IEEE J. Solid State Circuits 2002, 37, 751–759. [Google Scholar] [CrossRef]
- Kristoffersen, S.; Thingsrud, O. The EKKO II synthetic target generator for imaging radar. In Proceedings of the 5th European Conference on Synthetic Aperture Radar, Ulm, Germany, 25–27 May 2004; pp. 871–874. [Google Scholar]
- Wei, Y.; Hang, R.; Shuxian, Z.; Li, Y. Study of noise jamming based on convolution modulation to SAR. In Proceedings of the 2010 International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010; pp. 169–172. [Google Scholar]
- Garmatyuk, D.S.; Narayanan, R.M. ECCM capabilities of an ultrawideband bandlimited random noise imaging radar. IEEE Trans. Aerosp. Electron. Syst. 2002, 28, 1243–1255. [Google Scholar] [CrossRef]
- Yan, Z.; Guoqing, Z.; Yu, Z. Research on SAR jamming technique based on man-made map. In Proceedings of the International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar]
- Lin, X.; Liu, P.; Xue, G. Fast generation of SAR deceptive jamming signal based on inverse range doppler algorithm. In Proceedings of the IET International Radar Conference, Xi’an, China, 14–16 April 2013; pp. 1–4. [Google Scholar]
- Xiaodong, H.; Jun, Z.; Jun, W.; Dongping, D.; Bin, T. False target deception jamming for countering missile-borne SAR. In Proceedings of the IEEE 17th International Conference on Computational and Engineering, Chengdu, China, 19–21 December 2014; pp. 1974–1978. [Google Scholar]
- Feng, Z.; Bo, Z.; Mingliang, T.; Xueru, B.; Bo, C.; Guangcai, S. A Large scene deceptive jamming method for space-borne SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4486–4495. [Google Scholar] [CrossRef]
- Qingyang, S.; Ting, S.; Shicheng, Z.; Bin, T.; Wenxian, Y. A novel jamming signal generation method for deceptive SAR jammer. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1174–1178. [Google Scholar]
- Bo, Z.; Feng, Z.; Zheng, B. Deception jamming for squint SAR based on multiple receivers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3988–3998. [Google Scholar] [CrossRef]
- Bo, Z.; Lei, H.; Feng, Z.; Jihong, Z. Performance improvement of deception jamming against SAR based on minimum condition number. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1039–1055. [Google Scholar] [CrossRef]
- Qingyang, S.; Ting, S.; Kaibor, Y.; Wenxian, Y. Efficient deceptive jamming method of static and moving targets against SAR. IEEE Sens. J. 2018, 18, 3601–3618. [Google Scholar] [CrossRef]
- Yongcai, L.; Wei, W.; Xiaoyi, P.; Dahai, D.; Dejun, F. A Frequency-domain three-stage algorithm for active deception jamming against synthetic aperture radar. IET Radar Sonar Navig. 2014, 8, 639–646. [Google Scholar] [CrossRef]
- Yongcai, L.; Wei, W.; Xiaoyi, P.; Qixiang, F.; Guoyu, W. Inverse omega-K algorithm for the electromagnetic deception of synthetic aperture radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3037–3049. [Google Scholar] [CrossRef]
- Bo, Z.; Lei, H.; Jian, L.; Maliang, L.; Jinwei, W. Deceptive SAR jamming based on 1-bit sampling and time-varying thresholds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 939–950. [Google Scholar] [CrossRef]
- Yongcai, L.; Wei, W.; Xiaoyi, P.; Letao, X.; Guoyu, W. Influence of estimate error of radar kinematic parameter on deception jamming against SAR. IEEE Sens. J. 2016, 16, 5904–5911. [Google Scholar] [CrossRef]
- Franceschetti, G.; Guida, R.; Iodice, A.; Riccio, D.; Ruello, G. Efficient simulation of hybrid stripmap/spotlight SAR raw signals from extended scenes. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2385–2396. [Google Scholar] [CrossRef]
- Ahmed, S.K.; Laurent, F.F.; Eric, P. Efficient SAR raw data generation for anisotropic urban scenes based on inverse processing. IEEE Geosci. Remote Sens. Lett. 2009, 6, 757–761. [Google Scholar] [CrossRef]
- Ian, G.C.; Frank, H.W. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Boston, MA, USA, 2005; pp. 45–63. [Google Scholar]
- Yongcai, L.; Wei, W.; Xiaoyi, P.; Dahai, D. Effective region of active decoy jamming to SAR based on time-delay doppler-shift method. J. Radars 2013, 2, 46–53. [Google Scholar]
















| Carrier Frequency | Chirp Rate | PRI | Pulse Width | Platform Velocity | Shortest Slant Range | Antenna Aperture |
|---|---|---|---|---|---|---|
| 5.30 GHz | 0.72 MHz/μs | 0.79 ms | 41.74 μs | 7.06 km/s | 989 km | 10 m |
| Range Dimension | Azimuth Dimension | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| IRW (m) | MLPO (m) | PSLR (dB) | ISLR (dB) | IRW (m) | MLPO (m) | PSLR (dB) | ISLR (dB) | ||
| RDS | 7.73 | 0 | −11.78 | −12.57 | 6.77 | 0 | −17.24 | −19.50 | |
| TDFS-TS | 7.73 | 0 | −11.78 | −12.57 | 6.77 | 0 | −17.24 | −19.50 | |
| RDS | 7.73 | 0 | −11.78 | −12.57 | 6.88 | 0 | −13.47 | −15.05 | |
| TDFS-TS | 7.73 | 0 | −11.78 | −12.57 | 6.88 | 0 | −13.39 | −14.98 | |
| RDS | 7.73 | 0 | −11.78 | −12.57 | 7.39 | 5.04 | −14.46 | −14.90 | |
| TDFS-TS | 7.78 | −0.21 | −12.03 | −12.96 | 7.47 | 0 | −13.95 | −13.67 | |
| RDS | 7.73 | 0 | −11.77 | −12.57 | 7.53 | 5.52 | −15.03 | −14.24 | |
| TDFS-TS | 7.78 | −0.21 | −12.04 | −12.96 | 7.60 | 0.48 | −15.12 | −12.55 | |
| Range Dimension | Azimuth Dimension | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| IRW (m) | MLPO (m) | PSLR (dB) | ISLR (dB) | IRW (m) | MLPO (m) | PSLR (dB) | ISLR (dB) | ||
| RDS | 7.73 | 0 | −12.07 | −12.79 | 6.77 | 0 | −17.79 | −20.30 | |
| TDFS-TS | 7.73 | 0 | −12.07 | −12.79 | 6.77 | 0 | −17.79 | −20.30 | |
| RDS | 7.88 | −3.48 | −12.79 | −13.87 | 7.07 | −80.32 | −16.56 | −17.91 | |
| TDFS-TS | 7.88 | 7.69 | −12.94 | −13.92 | 7.15 | −0.98 | −18.76 | −17.83 | |
| RDS | 7.77 | 2.46 | −12.02 | −12.60 | 7.39 | 29.01 | −15.03 | −15.45 | |
| TDFS-TS | 7.74 | 0.01 | −11.68 | −12.48 | 7.34 | −0.01 | −14.59 | −14.96 | |
| RDS | 7.95 | −1.17 | −12.36 | −13.47 | 8.05 | −50.70 | −14.05 | −14.08 | |
| TDFS-TS | 8.16 | 7.73 | −13.29 | −14.87 | 8.34 | −0.57 | −15.95 | −14.28 | |
| TDFS-TS | RDS1 | TDFS-TS-WSC | BA | |
|---|---|---|---|---|
| Preprocessing | - | |||
| Real-time calculation |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Ye, W.; Ma, F.; Li, G.; Tong, Q. A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation. Remote Sens. 2020, 12, 53. https://doi.org/10.3390/rs12010053
Yang K, Ye W, Ma F, Li G, Tong Q. A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation. Remote Sensing. 2020; 12(1):53. https://doi.org/10.3390/rs12010053
Chicago/Turabian StyleYang, Kaizhi, Wei Ye, Fangfang Ma, Guojing Li, and Qian Tong. 2020. "A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation" Remote Sensing 12, no. 1: 53. https://doi.org/10.3390/rs12010053
APA StyleYang, K., Ye, W., Ma, F., Li, G., & Tong, Q. (2020). A Large-Scene Deceptive Jamming Method for Space-Borne SAR Based on Time-Delay and Frequency-Shift with Template Segmentation. Remote Sensing, 12(1), 53. https://doi.org/10.3390/rs12010053