Assimilating SMOS Brightness Temperature for Hydrologic Model Parameters and Soil Moisture Estimation with an Immune Evolutionary Strategy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Frameworks
2.1.1. Variable Infiltration Capacity Model
2.1.2. Radiative Transfer Model
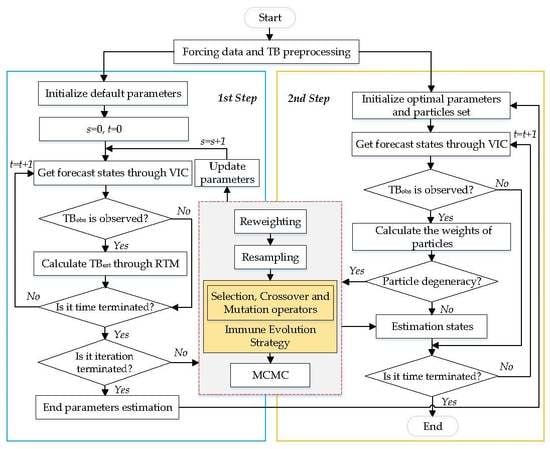
2.2. Data Assimilation Strategy
2.2.1. Bayesian Inference
2.2.2. Sequential Monte Carlo Sampling
2.2.3. Sequential Bayesian Estimation
2.2.4. Particle Filter-Markov Chain Monte Carlo
2.2.5. Immune Evolution Strategy
2.2.6. Data Assimilation Framework
2.3. Data
2.3.1. Study Area and In-Situ Observations
2.3.2. SMOS Brightness Temperature
2.3.3. SMOS Soil Moisture Products
2.3.4. Model Forcing
2.4. Data Assimilation Experiments
2.4.1. Experimental Design
2.4.2. Evaluation Metrics
3. Results
3.1. Evaluation of Parameters Estimation
3.2. Evaluation of Soil Moisture Estimation
3.3. Comparison with Other Soil Moisture Estimations
3.4. Comparison with Root Zone SM Estimates
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rains, D.; De Lannoy, G.J.M.; Lievens, H.; Walker, J.P.; Verhoest, N.E.C. SMOS and SMAP Brightness Temperature Assimilation Over the Murrumbidgee Basin. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1652–1656. [Google Scholar] [CrossRef]
- Parrens, M.; Wigneron, J.-P.; Richaume, P.; Mialon, A.; Al Bitar, A.; Fernandez-Moran, R.; Al-Yaari, A.; Kerr, Y.H. Global-scale surface roughness effects at L-band as estimated from SMOS observations. Remote Sens. Environ. 2016, 181, 122–136. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Kirby, J.M.; Mainuddin, M.; Ahmad, M.D.; Gao, L. Simplified Monthly Hydrology and Irrigation Water Use Model to Explore Sustainable Water Management Options in the Murray-Darling Basin. Water Resour. Manag. 2013, 27, 4083–4097. [Google Scholar] [CrossRef]
- Moradkhani, H. Hydrologic remote sensing and land surface data assimilation. Sensors 2008, 8, 2986–3004. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Xin, L.; Ling, L. Retrieving soil temperature profile by assimilating MODIS LST products with ensemble Kalman filter. Remote Sens. Environ. 2008, 112, 1320–1336. [Google Scholar] [CrossRef]
- Dumedah, G.; Coulibaly, P. Evolutionary assimilation of streamflow in distributed hydrologic modeling using in-situ soil moisture data. Adv. Water Resour. 2013, 53, 231–241. [Google Scholar] [CrossRef]
- Kolassa, J.; Reichle, R.H.; Draper, C.S. Merging active and passive microwave observations in soil moisture data assimilation. Remote Sens. Environ. 2017, 191, 117–130. [Google Scholar] [CrossRef]
- Rains, D.; Han, X.J.; Lievens, H.; Montzka, C.; Verhoest, N.E.C. SMOS brightness temperature assimilation into the Community Land Model. Hydrol. Earth Syst. Sci. 2017, 21, 5929–5951. [Google Scholar] [CrossRef] [Green Version]
- Gruber, A.; Lannoy, G.D.; Crow, W. A Monte Carlo based adaptive Kalman filtering framework for soil moisture data assimilation. Remote Sens. Environ. 2019, 228, 105–114. [Google Scholar] [CrossRef]
- Nair, A.S.; Indu, J. Improvement of land surface model simulations over India via data assimilation of satellite-based soil moisture products. J. Hydrol. 2019, 573, 406–421. [Google Scholar] [CrossRef]
- Bi, H.; Ma, J.; Wang, F. An Improved Particle Filter Algorithm Based on Ensemble Kalman Filter and Markov Chain Monte Carlo Method. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6134–6147. [Google Scholar] [CrossRef]
- Blankenship, C.B.; Case, J.L.; Zavodsky, B.T.; Crosson, W.L. Assimilation of SMOS Retrievals in the Land Information System. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6320–6332. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Moradkhani, H. Combined assimilation of streamflow and satellite soil moisture with the particle filter and geostatistical modeling. Adv. Water Resour. 2016, 94, 364–378. [Google Scholar] [CrossRef] [Green Version]
- De Lannoy, G.J.M.; Reichle, R.H. Global Assimilation of Multiangle and Multipolarization SMOS Brightness Temperature Observations into the GEOS-5 Catchment Land Surface Model for Soil Moisture Estimation. J. Hydrometeorol. 2016, 17, 669–691. [Google Scholar] [CrossRef] [Green Version]
- Kan, G.Y.; He, X.Y.; Li, J.R.; Ding, L.Q.; Hong, Y.; Zhang, H.B.; Liang, K.; Zhang, M.J. Computer Aided Numerical Methods for Hydrological Model Calibration: An Overview and Recent Development. Arch. Comput. Method Eng. 2019, 26, 35–59. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, L.; Chen, Y.Y.; Zhao, L.; Qin, J.; Lu, H.; Tang, W.J.; Han, M.L.; Ding, B.H.; Fang, N. Land surface model calibration through microwave data assimilation for improving soil moisture simulations. J. Hydrol. 2016, 533, 266–276. [Google Scholar] [CrossRef]
- Chen, W.J.; Shen, H.F.; Huang, C.L.; Li, X. Improving Soil Moisture Estimation with a Dual Ensemble Kalman Smoother by Jointly Assimilating AMSR-E Brightness Temperature and MODIS LST. Remote Sens. 2017, 9, 273. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; ter Braak, C.J.F.; Diks, C.G.H.; Schoups, G. Hydrologic data assimilation using particle Markov chain Monte Carlo simulation: Theory, concepts and applications. Adv. Water Resour. 2013, 51, 457–478. [Google Scholar] [CrossRef]
- Zhu, G.F.; Li, X.; Ma, J.Z.; Wang, Y.Q.; Liu, S.M.; Huang, C.L.; Zhang, K.; Hu, X.L. A new moving strategy for the sequential Monte Carlo approach in optimizing the hydrological model parameters. Adv. Water Resour. 2018, 114, 164–179. [Google Scholar] [CrossRef]
- Moradkhani, H.; Dechant, C.M.; Sorooshian, S. Evolution of ensemble data assimilation for uncertainty quantification using the particle filter-Markov chain Monte Carlo method. Water Resour. Res. 2012, 48, 120. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, 388. [Google Scholar] [CrossRef] [Green Version]
- Abbaszadeh, P.; Moradkhani, H.; Yan, H.X. Enhancing hydrologic data assimilation by evolutionary Particle Filter and Markov Chain Monte Carlo. Adv. Water Resour. 2018, 111, 192–204. [Google Scholar] [CrossRef]
- Fan, Y.; Leslie, D.S.; Wand, M.P. Generalised linear mixed model analysis via sequential Monte Carlo sampling. Electron. J. Stat. 2008, 2, 916–938. [Google Scholar] [CrossRef]
- Jeremiah, E.; Sisson, S.; Marshall, L.; Mehrotra, R.; Sharma, A. Bayesian calibration and uncertainty analysis of hydrological models: A comparison of adaptive Metropolis and sequential Monte Carlo samplers. Water Resour. Res. 2011, 47, 33. [Google Scholar] [CrossRef]
- Jeremiah, E.; Sisson, S.A.; Sharma, A.; Marshall, L. Efficient hydrological model parameter optimization with Sequential Monte Carlo sampling. Environ. Model. Softw. 2012, 38, 283–295. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of Surface- and Root-Zone ASCAT Soil Moisture Products into Rainfall-Runoff Modeling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Dumedah, G.; Moradkhani, H. Assessing model state and forecasts variation in hydrologic data assimilation. J. Hydrol. 2014, 513, 127–141. [Google Scholar] [CrossRef]
- DeChant, C.M.; Moradkhani, H. Examining the effectiveness and robustness of sequential data assimilation methods for quantification of uncertainty in hydrologic forecasting. Water Resour. Res. 2012, 48, 106. [Google Scholar] [CrossRef] [Green Version]
- Hartanto, I.M.; van der Kwast, J.; Alexandridis, T.K.; Almeida, W.; Song, Y.; van Andel, S.J.; Solomatine, D.P. Data assimilation of satellite-based actual evapotranspiration in a distributed hydrological model of a controlled water system. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 123–135. [Google Scholar] [CrossRef]
- Zhang, H.J.; Franssen, H.J.H.; Han, X.J.; Vrugt, J.A.; Vereecken, H. State and parameter estimation of two land surface models using the ensemble Kalman filter and the particle filter. Hydrol. Earth Syst. Sci. 2017, 21, 4927–4958. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef] [Green Version]
- Andrieu, C.; Doucet, A.; Holenstein, R. Particle Markov chain Monte Carlo methods. J. R. Stat. Soc. 2010, 72, 269–342. [Google Scholar] [CrossRef] [Green Version]
- Ju, F.; An, R.; Sun, Y.X. Immune Evolution Particle Filter for Soil Moisture Data Assimilation. Water 2019, 11, 211. [Google Scholar] [CrossRef] [Green Version]
- Penny, S.G.; Miyoshi, T. A local particle filter for high-dimensional geophysical systems. Nonlinear Process. Geophys. 2016, 23, 391–405. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.B.; van Leeuwen, P.J.; Amezcua, J. Implicit equal-weights particle filter. Q. J. R. Meteorol. Soc. 2016, 142, 1904–1919. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Su, J.B.; Lu, H.S.; Wang, J.Q.; Sadeghi, A.M.; Zhu, Y.H. Evaluating the Applicability of Four Latest Satellite-Gauge Combined Precipitation Estimates for Extreme Precipitation and Streamflow Predictions over the Upper Yellow River Basins in China. Remote Sens. 2017, 9, 1176. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Y.; Niu, J.; Kang, S.Z.; Zhang, X.T. Effects of irrigation on water and energy balances in the Heihe River basin using VIC model under different irrigation scenarios. Sci. Total Environ. 2018, 645, 1183–1193. [Google Scholar] [CrossRef]
- Park, D.; Markus, M. Analysis of a changing hydrologic flood regime using the Variable Infiltration Capacity model. J. Hydrol. 2014, 515, 267–280. [Google Scholar] [CrossRef]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44, 93. [Google Scholar] [CrossRef]
- Tesemma, Z.K.; Wei, Y.; Peel, M.C.; Western, A.W. The effect of year-to-year variability of leaf area index on Variable Infiltration Capacity model performance and simulation of runoff. Adv. Water Resour. 2015, 83, 310–322. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Al Bitar, A.; Verhoest, N.E.C.; Cabot, F.; De Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Franssen, H.J.H.; Kerr, Y.; Tomer, S.K.; et al. Optimization of a Radiative Transfer Forward Operator for Simulating SMOS Brightness Temperatures over the Upper Mississippi Basin. J. Hydrometeorol. 2015, 16, 1109–1134. [Google Scholar] [CrossRef] [Green Version]
- Parrens, M.; Wigneron, J.P.; Richaume, P.; Al Bitar, A.; Mialon, A.; Fernandez-Moran, R.; Al-Yaari, A.; O’Neill, P.; Kerr, Y. Considering combined or separated roughness and vegetation effects in soil moisture retrievals. Int. J. Appl. Earth Obs. Geoinf. 2017, 55, 73–86. [Google Scholar] [CrossRef]
- Mironov, V.; Kerr, Y.; Wigneron, J.P.; Kosolapova, L.; Demontoux, F. Temperature- and Texture-Dependent Dielectric Model for Moist Soils at 1.4 GHz. IEEE Geosci. Remote Sens. Lett. 2013, 10, 419–423. [Google Scholar] [CrossRef] [Green Version]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Owen, A.B.; Tribble, S.D. A quasi-Monte Carlo Metropolis algorithm. Proc. Natl. Acad. Sci. USA 2005, 102, 8844–8849. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Ding, Y.S.; Hao, K.R.; Cai, X. An adaptive immune algorithm for service-oriented agricultural Internet of Things. Neurocomputing 2019, 344, 3–12. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Y.S.; Jin, Y.C.; Hao, K.R. Immune-Endocrine System Inspired Hierarchical Coevolutionary Multiobjective Optimization Algorithm for IoT Service. IEEE Trans. Cybern. 2020, 50, 164–177. [Google Scholar] [CrossRef]
- Han, H.; Ding, Y.S.; Hao, K.R.; Liang, X. An evolutionary particle filter with the immune genetic algorithm for intelligent video target tracking. Comput. Math. Appl. 2011, 62, 2685–2695. [Google Scholar] [CrossRef] [Green Version]
- Bryan, B.A.; Gao, L.; Ye, Y.Q.; Sun, X.F.; Connor, J.D.; Crossman, N.D.; Stafford-Smith, M.; Wu, J.G.; He, C.Y.; Yu, D.Y.; et al. China’s response to a national land-system sustainability emergency. Nature 2018, 559, 193–204. [Google Scholar] [CrossRef]
- Su, Z.; Wen, J.; Dente, L.; van der Velde, R.; Wang, L.; Ma, Y.; Yang, K.; Hu, Z. The Tibetan Plateau observatory of plateau scale soil moisture and soil temperature (Tibet-Obs) for quantifying uncertainties in coarse resolution satellite and model products. Hydrol. Earth Syst. Sci. 2011, 15, 2303–2316. [Google Scholar] [CrossRef] [Green Version]
- Dente, L.; Vekerdy, Z.; Wen, J.; Su, Z. Maqu network for validation of satellite-derived soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 55–65. [Google Scholar] [CrossRef]
- Laura, D.; Zhongbo, S.; Jun, W. Validation of SMOS soil moisture products over the Maqu and Twente regions. Sensors 2012, 12, 9965–9986. [Google Scholar]
- Zeng, J.Y.; Li, Z.; Chen, Q.; Bi, H.Y.; Qiu, J.X.; Zou, P.F. Evaluation of remotely sensed and reanalysis soil moisture products over the Tibetan Plateau using in-situ observations. Remote Sens. Environ. 2015, 163, 91–110. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Fernandez-Moran, R.; Wigneron, J.P.; De Lannoy, G.; Lopez-Baeza, E.; Parrens, M.; Mialon, A.; Mahmoodi, A.; Al-Yaari, A.; Bircher, S.; Al Bitar, A.; et al. A new calibration of the effective scattering albedo and soil roughness parameters in the SMOS SM retrieval algorithm. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 27–38. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H. Assimilation of SMOS brightness temperatures or soil moisture retrievals into a land surface model. Hydrol. Earth Syst. Sci. 2016, 20, 4895–4911. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chai, L.N.; Lu, Z.; Liu, S.M.; Qu, Y.Q.; Geng, D.Y.; Song, Y.Z.; Guan, Y.B.; Guo, Z.X.; Wang, J.; et al. Evaluation of SMAP, SMOS-IC, FY3B, JAXA, and LPRM Soil Moisture Products over the Qinghai-Tibet Plateau and Its Surrounding Areas. Remote Sens. 2019, 11, 792. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Zeng, Y.J.; Su, Z.B.; van der Velde, R.; Wang, L.C.; Xu, K.; Wang, X.; Wen, J. Blending Satellite Observed, Model Simulated, and in Situ Measured Soil Moisture over Tibetan Plateau. Remote Sens. 2016, 8, 268. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.Y.; Yang, K.; Qin, J.; Cui, Q.; Lu, H.; La, Z.; Han, M.L.; Tang, W.J. Evaluation of SMAP, SMOS, and AMSR2 soil moisture retrievals against observations from two networks on the Tibetan Plateau. J. Geophys. Res. Atmos. 2017, 122, 5780–5792. [Google Scholar] [CrossRef]









| Parameter | Units | Description | Range |
|---|---|---|---|
| B | None | Infiltration shape parameter | 0–0.4 |
| Dsmax | mm day−1 | Maximum baseflow velocity | 0–30 |
| Ds | None | Fraction of Dsmax where nonlinear baseflow begins | 0–1 |
| Ws | None | Fraction of the maximum SM where nonlinear baseflow happens | 0–1 |
| d2 | m | Thickness of the upper layer | 0.1–2 |
| d3 | m | Thickness of the lower layer | 0.1–2 |
| SM | Unfrozen Period | Entire Simulation Period | ||||
|---|---|---|---|---|---|---|
| RMSE | MBE | R | RMSE | MBE | R | |
| OL_opt | 0.077 | 0.074 | 0.793 | 0.102 | 0.070 | 0.741 |
| OL_def | 0.108 | 0.105 | 0.824 | 0.126 | 0.106 | 0.751 |
| DA_opt | 0.088 | 0.073 | 0.732 | 0.087 | 0.059 | 0.808 |
| SM | RMSE | MBE | R |
|---|---|---|---|
| OL_opt | 0.024 | 0.013 | 0.699 |
| OL_def | 0.021 | 0.016 | 0.715 |
| DA_opt | 0.029 | 0.027 | 0.755 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, F.; An, R.; Yang, Z.; Huang, L.; Sun, Y. Assimilating SMOS Brightness Temperature for Hydrologic Model Parameters and Soil Moisture Estimation with an Immune Evolutionary Strategy. Remote Sens. 2020, 12, 1556. https://doi.org/10.3390/rs12101556
Ju F, An R, Yang Z, Huang L, Sun Y. Assimilating SMOS Brightness Temperature for Hydrologic Model Parameters and Soil Moisture Estimation with an Immune Evolutionary Strategy. Remote Sensing. 2020; 12(10):1556. https://doi.org/10.3390/rs12101556
Chicago/Turabian StyleJu, Feng, Ru An, Zhen Yang, Lijun Huang, and Yaxing Sun. 2020. "Assimilating SMOS Brightness Temperature for Hydrologic Model Parameters and Soil Moisture Estimation with an Immune Evolutionary Strategy" Remote Sensing 12, no. 10: 1556. https://doi.org/10.3390/rs12101556
APA StyleJu, F., An, R., Yang, Z., Huang, L., & Sun, Y. (2020). Assimilating SMOS Brightness Temperature for Hydrologic Model Parameters and Soil Moisture Estimation with an Immune Evolutionary Strategy. Remote Sensing, 12(10), 1556. https://doi.org/10.3390/rs12101556