Remote Sensing and Multi-Criteria Evaluation for Malaria Risk Mapping to Support Indoor Residual Spraying Prioritization in the Central Highlands of Madagascar
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Land Cover Update
2.3. Spatial Multi Criteria Evaluation
2.3.1. Criteria Identification and Differentiation
2.3.2. Factor Standardization
2.3.3. Factor Weighting
2.3.4. Criteria Aggregation
2.3.5. Validation of the Model Framework
2.4. Uncertainty Analyses
2.5. Plugin Development
2.6. Change Detection
3. Results
3.1. Land Cover Updating
3.2. Malaria Risk Model
3.3. Uncertainty Analysis
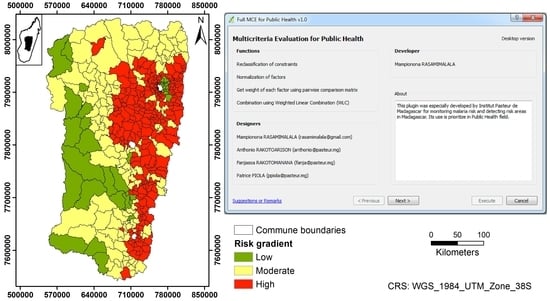
3.4. “MCE for Public Health” Plugin
3.5. Change Detection on Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. World Malaria Report 2019; World Health Organization: Geneva, Switzerland, 2019. [Google Scholar]
- Roll Back Malaria. RBM Partenership Strategic Plan 2018–2020; RBM Partnership to end Malaria: Geneva, Switzerland, 2018. [Google Scholar]
- Direction de Lutte contre le Paludisme. Plan Stratégique National de lutte contre le paludisme 2018–2022; Direction de Lutte contre le Paludisme: Antananarivo, Madagascar, 2017.
- INSTAT. Enquête sur les indicateurs du Paludisme à Madagascar—Rapport Final 2016; INSTAT: Calverton, MD, USA, 2017. [Google Scholar]
- Mouchet, J.; Baudon, D. Rapport de Mission d’expertise sur le Paludisme à Madagascar (Région des Hauts Plateaux); Ministère de la Coopération et du Développement: Paris, France, 1988.
- Randrianasolo, L.; Raoelina, Y.; Ratsitorahina, M.; Ravolomanana, L.; Andriamandimby, S.; Heraud, J.; Rakotomanana, F.; Ramanjato, R.; Randrianarivo-Solofoniaina, A.E.; Richard, V. Sentinel surveillance system for early outbreak detection in Madagascar. BMC Public Health 2010, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rabarijaona, L.P.; Rabe, T.; Ranaivo, L.H.; Raharimalala, L.A.; Rakotomanana, F.; Rakotondraibe, E.M.; Ramarosandratana, B.; Rakotoson, J.D.; Rakotonjanabelo, L.A.; Tafangy, P.B. Paludisme sur les Hautes Terres Centrales de Madagascar: Stratégies de lutte. Méd. Trop. 2006, 66, 504–512. [Google Scholar]
- Ratovonjato, J.; Randrianarivelojosia, M.; Rakotondrainibe, M.E.; Raharimanga, V.; Andrianaivolambo, L.; Le Goff, G.; Rogier, C.; Ariey, F.; Boyer, S.; Robert, V. Entomological and parasitological impacts of indoor residual spraying with DDT, alphacypermethrin and deltamethrin in the western foothill area of Madagascar. Malar. J. 2014, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- The Global Fund. The Global Fund 2016 Annual Financial Report; The Global Fund: Geneva, Switzerland, 2017. [Google Scholar]
- PMI. Malaria Operational Plan FY 2018; PMI: Washington, WA, USA, 2018. [Google Scholar]
- Jambou, R.; Ranaivo, L.; Raharimalala, L.; Randrianarivo, J.; Rakotomanana, F.; Modiano, D.; Pietra, V.; Boisier, P.; Rabarijaona, L.; Rabe, T.; et al. Malaria in the highlands of Madagascar after five years of indoor house spraying of DDT. Trans. R. Soc. Trop. Med. Hyg. 2001, 95, 14–18. [Google Scholar] [CrossRef]
- Robert, V.; Le Goff, G.; Andrianaivolambo, L.; Randimby, F.M.; Domarle, O.; Randrianarivelojosia, M.; Raharimanga, V.; Raveloson, A.; Ravaonjanahary, C.; Ariey, F. Moderate transmission but high prevalence of malaria in Madagascar. Int. J. for Parasitol. 2006, 36, 1273–1281. [Google Scholar] [CrossRef]
- Nepomichene, T.; Tata, E.; Boyer, S. Malaria case in Madagascar, probable implication of a new vector, Anopheles coustani. Malar. J. 2015, 14, 475. [Google Scholar] [CrossRef] [Green Version]
- Rincón-Romero, M.E.; Londoño, J.E. Mapping malaria risk using environmental and anthropic variables. Rev. Bras. Epidemiol. 2009, 12, 338–354. [Google Scholar] [CrossRef] [Green Version]
- Ferrao, J.L.; Niquisse, S.; Mendes, J.M.; Painho, M. Mapping and Modelling Malaria Risk Areas Using Climate, Socio-Demographic and Clinical Variables in Chimoio, Mozambique. Int. J. Environ. Res. Public Health 2018, 15, 795. [Google Scholar] [CrossRef] [Green Version]
- Kleinschmidt, I.; Bagayoko, M.; Clarke, G.P.Y.; Craig Le Sueur, D. A spatial statistical approach to malaria mapping. Int. J. Epidemiol. 2000, 29, 355–361. [Google Scholar] [CrossRef] [Green Version]
- Yankson, R.; Anto, E.A.; Chipeta, M.G. Geostatistical analysis and mapping of malaria risk in children under 5 using point-referenced prevalence data in Ghana. Malar. J. 2019, 18, 67. [Google Scholar] [CrossRef] [Green Version]
- Hanaf-Bojd, A.A.; Vatandoost, H.; Oshaghi, M.A.; Charrahy, Z.; Haghdoost, A.A.; Zamani, G.; Abedi, F.; Sedaghat, M.M.; Soltani, M.; Shahi, M.; et al. Spatial analysis and mapping of malaria risk in an endemic area, south of Iran: A GIS based decision making for planning of control. Acta Trop. 2012, 122, 132–137. [Google Scholar] [CrossRef] [PubMed]
- Wondim, Y.K.; Alemayehu, E.B.; Abebe, W.B. Malaria Hazard and Risk Mapping Using GIS Based Spatial Multicriteria Evaluation Technique (SMCET) in Tekeze Basin Development Corridor, Amhara Region, Ethiopia. J. Environ. Earth Sci. 2017, 7, 5. [Google Scholar]
- Ali, S.K.A.; Ahmad, A. Mapping of mosquito-borne diseases in Kolkata Municipal Corporation using GIS and AHP based decision making approach. Spat. Inf. Res. 2019, 27, 351–372. [Google Scholar] [CrossRef]
- Reinhold, J.M.; Lazzari, C.R.; Lahondère, C. Effects of the Environmental Temperature on Aedes aegypti and Aedes albopictus Mosquitoes: A Review. Insects 2018, 9, 158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rakotomanana, F.; Randremanana, R.V.; Rabarijaona, L.P.; Duchemin, J.B.; Ratovonjato, J.; Ariey, F.; Rudant, J.P.; Jeanne, I. Determining areas that require indoor insecticide spraying using Multi Criteria Evaluation, a decision-support tool for malaria vector control programmes in the Central Highlands of Madagascar. Int. J. Health Geogr. 2007, 6. [Google Scholar] [CrossRef] [Green Version]
- Zahouli, J.B.Z.; Koudou, B.G.; Müller, P.; Malone, D.; Tano, Y.; Utzinger, J. Effect of land-use changes on the abundance, distribution, and host-seeking behavior of Aedes arbovirus vectors in oil palm-dominated landscapes, southeastern Côte d’Ivoire. PLoS ONE 2017, 12, e0189082. [Google Scholar] [CrossRef]
- Gimonneau, G.; Bouyer, J.; Morand, S.; Besansky, N.J.; Diabate, A.; Simard, F. A behavioral mechanism underlying ecological divergence in the malaria mosquito Anopheles gambiae. Behav. Ecol. 2010, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Paaijmans, K.P.; Thomas, M.B. The influence of mosquito resting behaviour and associated microclimate for malaria risk. Malar. J. 2011, 10. [Google Scholar] [CrossRef] [Green Version]
- Tran, A.; Ponçon, N.; Toty, C.; Linard, C.; Guis, H.; Ferré, J.B.; Lo Seen, D.; Roger, F.; de la Rocque, S.; Fontenille, D.; et al. Using remote sensing to map larval and adult populations of Anopheles hyrcanus (Diptera: Culicidae) a potential malaria vector in Southern France. Int. J. Health Geogr. 2008, 7, 9. [Google Scholar] [CrossRef] [Green Version]
- Machault, V.; Vignolles, C.; Borchi, F.; Vounatsou, P.; Pages, F.; Briolant, S.; Lacaux, J.P.; Rogier, C. The use of remotely sensed environmental data in the study of malaria. Geospat. Health 2011, 5, 151–168. [Google Scholar] [CrossRef] [Green Version]
- Machault, V.; Vignolles, C.; Pagès, F.; Gadiaga, L.; Tourre, Y.M.; Gaye, A.; Sokhna, C.; Trape, J.-F.; Lacaus, J.-P.; Rogier, C. Risk mapping of Anopheles gambiae s.l. densities using remotely-sensed environmental and meteorological data in an urban area: Dakar, Senegal. PLoS ONE. 2012, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tokarz, R.; Novak, R.J. Spatial–temporal distribution of Anopheles larval habitats in Uganda using GIS/remote sensing technologies. Malar. J. 2018, 17, 420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Booman, M.; Durrheim, D.N.; La Grange, K.; Martin, C.; Mabuza, A.M.; Zitha, A.; Mbokazi, F.M.; Fraser, C.; Sharp, B.L. Using a geographical information system to plan a malaria control programme in South Africa. Bull. World Health Organ. 2000, 78, 1438–1444. [Google Scholar] [PubMed]
- Carter, R.; Mendis, K.N.; Roberts, D. Spatial targeting of interventions against malaria. Bull. World Health Organ. 2000, 78, 1401–1411. [Google Scholar] [PubMed]
- Samadoulougou, S.; Maheu-Giroux, M.; Kirakoya-Samadoulougou, F.; De Keukeleire, M.; Castro, M.C.; Robert, A. Multilevel and geo-statistical modeling of malaria risk in children of Burkina Faso. Parasites Vectors 2014, 7, 350. [Google Scholar] [CrossRef] [Green Version]
- Millar, J.; Psychas, P.; Abuaku, B.; Ahorlu, C.; Amratia, P.; Koram, K.; Oppong, S.; Valle, D. Detecting local risk factors for residual malaria in northern Ghana using Bayesian model averaging. Malar. J. 2018, 17, 343. [Google Scholar] [CrossRef] [Green Version]
- Hongoh, V.; Hoen, A.G.; Aenishaenslin, C.; Waaub, J.-P.; Bélanger, D.; Michel, P. The Lyme-MCDA Consortium. Spatially explicit multi-criteria decision analysis for managing vector-borne diseases. Int. J. Health Geogr. 2011, 10, 70. [Google Scholar] [CrossRef] [Green Version]
- Chevalier, V.; Trevennec, C.; Gély, M.; Pinto, J.; Tran, A. Spatial multi-criteria evaluation: A promising methodology for identifying areas at risk of Rift Valley fever. EMPRES-Anim. Health 2014, 360, 14–16. [Google Scholar]
- Tran, A.; Roger, F. Strengthening health decision-making at the territorial level: Operational support for spatial multi-criteria evaluation. CIRAD Montp. Perspect. 2018, 46, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Chandio, I.A.; Matori, A.N.B.; Yusof, K.B.W.; Talpur, M.A.H. Validation of Multi-Criteria Decision Analysis model of land suitability analysis for sustainable hillside development. Eur. J. Sci. Res. 2013, 109, 342–349. [Google Scholar]
- Cinelli, M.; Coles, S.R.; Kirwan, K. Analysis of the potentials of multi criteria decision analysis methods to conduct sustainability assessment. Ecol. Indic. 2014, 46, 138–148. [Google Scholar] [CrossRef] [Green Version]
- Dehe, B.; Bamford, D. Development, test and comparison of two Multiple Criteria Decision Analysis (MCDA) models: A case of healthcare infrastructure location. Expert Syst. Appl. 2015, 42, 6717–6727. [Google Scholar] [CrossRef] [Green Version]
- Thiery, Y.; Malet, J.-P.; Maquaire, O. Test of fuzzy logic rules for landslide susceptibility assessment. In Proceedings of the International Conference on Spatial Analysis and Geomatics, Strasbourg, France, 11–13 September 2006. [Google Scholar]
- Eastman, J.R.; Jin, W.; Kyem, P.A.K.; Toledano, J. Raster procedures for multi-criteria/multi-objective decisions. Photogramm. Eng. Remote Sens. 1995, 61, 539–547. [Google Scholar]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Pechanec, V.; Machar, I. Implementation of decision support tools in ArcGIS and IDRISI and their environmental applications. Int. J. Circuits Syst. Signal Process. 2014, 8, 388–398. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Carnevale, P.; Robert, V. Les anopheles Biologie, transmission du Plasmodium et lutte antivectorielle; IRD: Marseille, France, 2009. [Google Scholar]
- Afrane, Y.A.; Githeko, A.; Yan, G. The ecology of Anopheles mosquitoes under climate change: Cases studies from the effects of environmental changes in East Africa highlands. Ann. N.Y. Acad. Sci. 2012, 1249, 204–210. [Google Scholar] [CrossRef]
- Beck-johnson, L.M.; Nelson, W.A.; Paaijmans, K.P.; Read, A.F.; Thomas, M.B.; Bjørnstad, O.N. The effect of temperature on Anopheles mosquito population dynamics and the potential for malaria transmission. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Ewing, D.A.; Cobbold, C.A.; Purse, B.V.; Nunn, M.A.; White, S.M. Modelling the effect of temperature on the seasonal population dynamics of temperate mosquitoes. J. Theor. Biol. 2016, 400, 65–79. [Google Scholar] [CrossRef] [Green Version]
- Depinay, J.O.; Mbogo, C.M.; Killeen, G.; Knols, B.; Beier, J.; Carlson, J.; Dushoff, J.; Billingsley, P.; Mwambi, H.; Githure, J.; et al. A simulation model of African Anopheles ecology and population dynamics for the analysis of malaria transmission. Malar. J. 2004, 3. [Google Scholar] [CrossRef] [Green Version]
- Paaijmans, K.P.; Imbahale, S.S.; Thomas, M.B.; Takken, W. Relevant microclimate for determining the development rate of malaria mosquitoes and possible implications of climate change. Malar. J. 2010, 9, 196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galardo, A.K.R.; Zimmerman, R.H.; Lounibos, L.P.; Young, L.J.; Galardo, C.D.; Arruda, M.; D’Almeida Couto, A.A.R. Seasonal abundance of anopheline mosquitoes and their association with rainfall and malaria along the Matapi River, Amap, Brazil. Med. Vet. Entomol. 2009, 23, 335–349. [Google Scholar] [CrossRef] [PubMed]
- Kelly-hope, L.A.; Hemingway, J.; Mckenzie, F.E. Environmental factors associated with the malaria vectors Anopheles gambiae and Anopheles funestus in Kenya. Malar. J. 2009, 8, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravoniharimelina, B.; Romi, R.; Sabatinelli, G. Etude longitudinale sur les gîtes larvaires d’Anopheles gambiae s. l. dans un canton de la province d’Antananarivo (Hautes Terres Centrales de Madagascar). Ann. Parasitol. Hum. Comp. 1992, 67, 26–30. [Google Scholar] [CrossRef]
- Kaufmann, C.; Briegel, H. Flight performance of the malaria vectors Anopheles gambiae and Anopheles atroparvus. J. Vector Ecol. 2004, 29, 140–153. [Google Scholar]
- Eastman, J.R. Multi-criteria evaluation and GIS. In Geographical Information Systems; John Wiley and Sons: Hoboken, NJ, USA, 1999; pp. 493–502. ISBN 978-0-470-87002-0. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2005; ISBN 0131453610. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Arlinghaus, S.L.; Kerski, J.J. Spatial Mathematics: Theory and Practice through Mapping; Taylor & Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Scrucca, L.; Fop, M.; Murphy, T.B.; Raftery, A.E. mclust 5: Clustering, Classification and Density Estimation Using Gaussian Finite Mixture Models. R J. 2016, 8, 289. [Google Scholar] [CrossRef] [Green Version]
- Nandi, A.; Shakoor, A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng. Geol. 2009, 110, 11–20. [Google Scholar] [CrossRef]
- Ligmann-zielinska, A.; Jankowski, P. Spatially-explicit integrated uncertainty and sensitivity analysis of criteria weights in multicriteria land suitability evaluation. Environ. Model. Softw. 2014, 57, 235–247. [Google Scholar] [CrossRef]
- Paul, M.C.; Goutard, F.L.; Roulleau, F.; Holl, D.; Thanapongtharm, W.; Roger, F.L.; Tran, A. Quantitative assessment of a spatial multicriteria model for highly pathogenic avian influenza H5N1 in Thailand, and application in Cambodia. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, A.; Trevennec, C.; Lutwama, J.; Sserugga, J.; Gély, M.; Pittiglio, C.; Pinto, J.; Chevalier, V. Development and assessment of a geographic knowledge-based model for mapping suitable areas for rift valley fever transmission in Eastern Africa. PLoS Negl. Trop. Dis. 2016, 10, e0004999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Summerfield, M. Rapid GUI Programming with Python and Qt, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2007; ISBN 0-13-235418-9. [Google Scholar]
- Singh, A. Digital change detection techniqus using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef] [Green Version]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2000; Chapter 5; ISBN 0471356328. [Google Scholar]
- Kindu, M.; Schneider, T.; Teketay, D.; Knoke, T. Land Use/Land Cover change analysis using object-based classification approach in Munessa-Shashemene landscape of the Ethiopian Highlands. Remote Sens. 2013, 5, 2411–2435. [Google Scholar] [CrossRef] [Green Version]
- Phiri, D.; Morgenroth, J. Developments in Landsat land cover classification methods: A review. Remote Sens. 2017, 9, 967. [Google Scholar] [CrossRef] [Green Version]
- Bhatt, B.; Joshi, J. Analytical hierarchy process modeling for malaria risk zones in Vadodara district, Gujarat. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2014, XL-8, 171–176. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A. GIS and remote sensing for malaria risk mapping, Ethiopia. ISPRS Tech. Comm. VIII Symp. 2014, XL-8, 155–161. [Google Scholar] [CrossRef] [Green Version]
- Lawpoolsri, S.; Chavez, I.F.; Yimsamran, S.; Puangsa-art, S.; Thanyavanich, N.; Maneeboonyang, W.; Chaimungkun, W.; Singhasivanon, P.; Maguire, J.H.; Hungerford, L.L. The impact of human reservoir of malaria at a community-level on individual malaria occurrence in a low malaria transmission setting along the Thai-Myanmar border. Malar. J. 2010, 9, 143. [Google Scholar] [CrossRef] [Green Version]
- Ouédraogo, A.L.; Gonçalves, B.P.; Gnémé, A.; Wenger, E.A.; Guelbeogo, M.W.; Ouédraogo, A.; Gerardin, J.; Bever, C.A.; Lyons, H.; Pitroipa, X.; et al. Dynamics of the human infectious reservoir for malaria determined by mosquito feeding assays and ultrasensitive malaria diagnosis in Burkina Faso. J. Infect. Dis. 2016, 213, 90–99. [Google Scholar] [CrossRef] [Green Version]
- Chanda, E.; Mukonka, V.M.; Mthembu, D.; Kamuliwo, M.; Coetzer, S.; Shinondo, C.J. Using a Geographical Information System based decision support to enhance malaria vector control in Zambia. J. Trop. Med. 2012, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinchoff, J.; Larsen, D.A.; Renn, S.; Pollard, D.; Fornadel, C.; Maire, M.J.; Sikaala, C.; Sinyangwe, C.; Winters, B.; Bridges, D.J.; et al. Targeting indoor residual spraying for malaria using epidemiological data: A case study of the Zambia experience. Malar. J. 2016, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landman, W.A. How the International Research Institute fo Climate and Society has contributed towards seasonal climate foecast modelling and operations in South Africa. Earth Perspect. 2014, 1, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Gaudart, J.; Touré, O.; Dessay, N.; Dicko, A.L.; Ranque, S.; Forest, L.; Demongeot, J.; Doumbo, O.K. Modelling malaria incidence with environmental dependency in a locality of Sudanese savannah area, Mali. Malar. J. 2009, 8. [Google Scholar] [CrossRef]
- Dambach, P.; Machault, V.; Lacaus, J.-P.; Vignolles, C.; Sié, A.; Sauerborn, R. Utilization of combined remote sensing techniques to detect environmental variables influencing malaria vector densities in rural West Africa. Int. J. Health Geogr. 2012, 11. [Google Scholar] [CrossRef] [Green Version]
- Howes, R.E.; Mioramalala, S.A.; Ramiranirina, B.; Franchard, T.; Rakotorahalahy, A.J.; Bisanzio, D.; Gething, P.W.; Zimmerman, P.A.; Ratsimbasoa, A. Contemporary epidemiological overview of malaria in Madagascar: Operational utility of reported routine case data for malaria control planning. Malar. J. 2016, 15, 502. [Google Scholar] [CrossRef] [Green Version]
- Ihantamalala, F.A.; Rakotoarimanana, F.M.J.; Ramiadantsoa, T.; Rakotondramanga, J.M.; Pennober, G.; Rakotomanana, F.; Simon Cauchemez, C.J. Spatial and temporal dynamics of malaria in Madagascar. Malar. J. 2018, 17, 58. [Google Scholar] [CrossRef]
- Girond, F.; Randrianasolo, L.; Randriamampionona, L.; Rakotomanana, F.; Randrianarivelojosoa, M.; Ratsitorahina, M.; Brou, T.Y.; Herbreteau, V.; Mangeas, M.; Zigiumugabe, S.; et al. Analysing trends and forecasting malaria epidemics in Madagascar using a sentinel surveillance network: A web-based application. Malar. J. 2017, 16, 72. [Google Scholar] [CrossRef]
- Chakhar, S. Enhancing Geographical Information Systems Capabilities with Multi-Criteria Evaluation Functions. J. Geogr. Inf. Decis. Anal. 2003, 7, 47–71. [Google Scholar]








| Classes | Parameters |
|---|---|
| Rice field | GLCM contrast ≤ 70; LWM ≤ 75; Mean layer ≤ 85 |
| Water body | NDWI > 0.37; Sum of reflectance (Σ (b2, b3, b3)) < 204 |
| Hydrographic network | Brightness > 65; LWM < 56; NDVI < 0 |
| Wet cultivation | −0.15 < NDVI < −0.01 |
| Other | Everything that is not assigned to the above four classes |
| Criteria | Description |
|---|---|
| Inhabited zone | BF: recoded to 1 for inhabited areas that are potentially at risk, and to 0 for uninhabited area that are not at risk |
| Elevation | BF: recoded to 0 for elevation <1000 m (permanent risk) and >1500 m (no risk); recoded to 1 for elevation between 1000 m and 1500 m |
| Population density | BF: recoded to 1 in areas with d <800 pop/km² and to 0 in areas with d ≥800 pop/km² |
| Criteria | Function | Control Points | |||
|---|---|---|---|---|---|
| a | b | c | d | ||
| Population density | Decreasing sigmoid | - | - | 400 ≤ d < 800 | d ≥ 800 |
| Elevation | Increasing sigmoid | 500 | 1500 | - | - |
| Distance to wetland | Decreasing sigmoid | - | - | 1000 | 5000 |
| Precipitation | Symmetric sigmoid | 0 | 80 | 1000 | 2000 |
| Temperature | Symmetric sigmoid | 18 | 28 | 32 | 35 |
| Kappa Index | |
|---|---|
| Land cover classification (2014) | 0.7741 |
| Land cover classification (2015) | 0.7438 |
| Land cover classification (2016) | 0.8320 |
| Factors | Weights |
|---|---|
| Population density | 0.4990 |
| Distance to wetland | 0.1824 |
| Temperature | 0.1698 |
| Elevation | 0.0910 |
| Precipitation | 0.0577 |
| 2015 Annual Parasite Incidence | ||
|---|---|---|
| 2016 Model Output | High | Low |
| High | TP: 111 | FP: 49 |
| Low | FN: 11 | TN: 37 |
| Accuracy: 0.712 Sensitivity: 0.910 Specificity: 0.430 | ||
| Surface 2015–2014 (km²) | Surface 2016–2015 (km²) | |
|---|---|---|
| decrease | 12,198.96 | 21,435.32 |
| no change | 12,334.38 | 3883.71 |
| increase | 10,086.82 | 9301.13 |
| Total | 34,620.16 | 34,620.16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakotoarison, H.A.; Rasamimalala, M.; Rakotondramanga, J.M.; Ramiranirina, B.; Franchard, T.; Kapesa, L.; Razafindrakoto, J.; Guis, H.; Tantely, L.M.; Girod, R.; et al. Remote Sensing and Multi-Criteria Evaluation for Malaria Risk Mapping to Support Indoor Residual Spraying Prioritization in the Central Highlands of Madagascar. Remote Sens. 2020, 12, 1585. https://doi.org/10.3390/rs12101585
Rakotoarison HA, Rasamimalala M, Rakotondramanga JM, Ramiranirina B, Franchard T, Kapesa L, Razafindrakoto J, Guis H, Tantely LM, Girod R, et al. Remote Sensing and Multi-Criteria Evaluation for Malaria Risk Mapping to Support Indoor Residual Spraying Prioritization in the Central Highlands of Madagascar. Remote Sensing. 2020; 12(10):1585. https://doi.org/10.3390/rs12101585
Chicago/Turabian StyleRakotoarison, Hobiniaina Anthonio, Mampionona Rasamimalala, Jean Marius Rakotondramanga, Brune Ramiranirina, Thierry Franchard, Laurent Kapesa, Jocelyn Razafindrakoto, Hélène Guis, Luciano Michaël Tantely, Romain Girod, and et al. 2020. "Remote Sensing and Multi-Criteria Evaluation for Malaria Risk Mapping to Support Indoor Residual Spraying Prioritization in the Central Highlands of Madagascar" Remote Sensing 12, no. 10: 1585. https://doi.org/10.3390/rs12101585
APA StyleRakotoarison, H. A., Rasamimalala, M., Rakotondramanga, J. M., Ramiranirina, B., Franchard, T., Kapesa, L., Razafindrakoto, J., Guis, H., Tantely, L. M., Girod, R., Rakotoniaina, S., Baril, L., Piola, P., & Rakotomanana, F. (2020). Remote Sensing and Multi-Criteria Evaluation for Malaria Risk Mapping to Support Indoor Residual Spraying Prioritization in the Central Highlands of Madagascar. Remote Sensing, 12(10), 1585. https://doi.org/10.3390/rs12101585