Strong Interrelation between the Short-Term Variability in the Ionosphere, Upper Mesosphere, and Winter Polar Stratosphere
Abstract
:1. Introduction
2. Methodology
2.1. TEC Variability Analysis Method
2.2. Mesopause Temperature Variability Analysis Method
3. Results
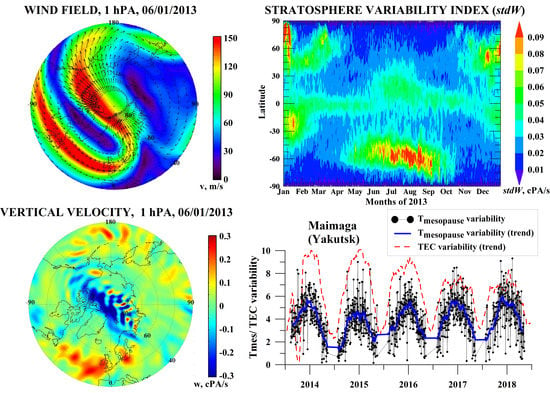
3.1. Ionosphere Variability Dynamics
3.2. Upper Mesosphere Variability Dynamics
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hocke, K.; Schlegel, K. A review of atmospheric gravity waves and travelling ionospheric disturbances: 1982–1995. Annal. Geophys. 1996, 14, 917–940. [Google Scholar] [CrossRef]
- Kazimirovsky, E.S. Coupling from below as a source of ionospheric variability: A review. Ann. Geophys. 2002, 45, 1–29. [Google Scholar] [CrossRef]
- Lastovicka, J. Forcing of the ionosphere by waves from below. J. Atmos. Sol. Terr. Phys. 2006, 68, 479–497. [Google Scholar] [CrossRef]
- Vadas, S.L. Horizontal and vertical propagation of gravity waves in thermosphere from lower atmospheric and thermospheric sources. J. Geophys. Res. 2007, 112, A06305. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef] [Green Version]
- Rishbeth, H.; Mendillo, M. Patterns of F2-layer variability. J. Atmos. Sol. Terr. Phys. 2001, 63, 1661–1680. [Google Scholar] [CrossRef]
- Forbes, J.M.; Palo, S.E.; Zhang, X. Variability of the ionosphere. J. Atmos. Sol. Terr. Phys. 2000, 62, 685–693. [Google Scholar] [CrossRef]
- Liu, H.-L.; Yudin, V.A.; Roble, R.G. Day-to-day ionospheric variability due to lower atmosphere perturbations. Geophys. Res. Lett. 2013, 40, 665–670. [Google Scholar] [CrossRef]
- Brasseur, G.; Solomon, S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of Stratosphere and Mesosphere, 3rd ed.; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Noll, S.; Kausch, W.; Kimeswenger, S.; Unterguggenberger, S.; Jones, A.M. OH populations and temperatures from simultaneous spectroscopic observations of 25 bands. Atmos. Chem. Phys. 2015, 15, 3647–3669. [Google Scholar] [CrossRef] [Green Version]
- Taylor, M.J.; Hapgood, M.A. On the origin of ripple-type wave structure in the OH nightglow emission. Planet Space Sci. 1990, 38, 1421–1430. [Google Scholar] [CrossRef]
- Nakamura, T.; Higashikawa, A.; Tsuda, T.; Matsushita, Y. Seasonal variations of gravity wave structures in OH airglow with a CCD imager at Shigaraki. Earth Planets Space 1999, 51, 897–906. [Google Scholar] [CrossRef] [Green Version]
- Vadas, S.L.; Taylor, M.J.; Pautet, P.-D.; Stamus, P.A.; Fritts, D.C.; Liu, H.-L.; São Sabbas, F.T.; Rampinelli, V.T.; Batista, P.; Takahashi, H. Convection: The likely source of the medium-scale gravity waves observed in the OH airglow layer near Brasilia, Brazil, during the SpreadFEx campaign. Ann. Geophys. 2009, 27, 231–259. [Google Scholar] [CrossRef] [Green Version]
- Offermann, D.; Wintel, J.; Kalicinsky, C.; Knieling, P.; Koppmann, R.; Steinbrecht, W. Long-term development of short-period gravity waves in middle Europe. J. Geophys. Res. 2011, 116, D00P07. [Google Scholar] [CrossRef] [Green Version]
- Gavrilov, N.M.; Manson, A.H.; Meek, C.E. Climatological monthly characteristics of middle atmosphere gravity waves (10 min–10 hr) during 1979–1993 at Saskatoon. Ann. Geophys. 1995, 13, 285–295. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Fukao, S.; Nakamura, T.; Jacobi, C.; Kürschner, D.; Manson, A.H.; Meek, C.E. Comparative study of interannual changes of the mean winds and gravity wave activity in the middle atmosphere over Japan, Central Europe and Canada. J. Atmos. Solar-Terr. Phys 2002, 64, 1003–1010. [Google Scholar] [CrossRef]
- Popov, A.A.; Gavrilov, N.M.; Andreev, A.B.; Pogoreltsev, A.I. Interannual dynamics in intensity of mesoscale hydroxyl nightglow variations over Almaty. Sol. Terr. Phys. 2018, 4, 63–68. [Google Scholar] [CrossRef]
- Taylor, M.J.; Pautet, P.-D.; Fritts, D.C.; Kaifler, B.; Smith, S.M.; Zhao, Y.; Criddle, N.R.; McLaughlin, P.; Pendleton, W.R.; McCarthy, M.P.; et al. Large-amplitude mountain waves in the mesosphere observed on 21 June 2014 during DEEPWAVE: 1. Wave development, scales, momentum fluxes, and environmental sensitivity. J. Geophys. Res. Atmos. 2019, 10, 364–384. [Google Scholar] [CrossRef] [Green Version]
- Medvedeva, I.; Ratovsky, K. Studying atmospheric and ionospheric variabilities from long-term spectrometric and radio sounding measurements. J. Geophys. Res. Space Phys. 2015, 120, 5151–5159. [Google Scholar] [CrossRef]
- Araujo-Pradere, E.A.; Fuller-Rowell, T.J.; Codrescu, M.V.; Bilitza, D. Characteristics of the ionospheric variability as a function of season latitude local time and geomagnetic activity. Radio Sci. 2005, 40, RS5009. [Google Scholar] [CrossRef]
- Altadill, D. Time/altitude electron density variability above Ebro, Spain. Adv. Space Res. 2007, 39, 962–969. [Google Scholar] [CrossRef]
- Ratovsky, K.G.; Medvedev, A.V.; Tolstikov, M.V. Diurnal, seasonal and solar activity pattern of ionospheric variability from Irkutsk Digisonde data. Adv. Space Res. 2015, 55, 2041–2047. [Google Scholar] [CrossRef]
- Frissell, N.A.; Baker, J.B.H.; Ruohoniemi, J.M.; Gerrard, A.J.; Miller, E.S.; Marini, J.P.; West, M.L.; Bristow, W.A. Climatology of medium-scale traveling ionospheric disturbances observed by the midlatitude Blackstone SuperDARN radar. J. Geophys. Res. Space Phys. 2014, 119, 7679–7697. [Google Scholar] [CrossRef]
- Frissell, N.A.; Baker, J.B.H.; Ruohoniemi, J.M.; Greenwald, R.A.; Gerrard, A.J.; Miller, E.S.; West, M.L. Sources and characteristics of medium-scale traveling ionospheric disturbances observed by high-frequency radars in the North American sector. J. Geophys. Res. Space Phys. 2016, 121, 3722–3739. [Google Scholar] [CrossRef]
- Kotake, N.; Otsuka, Y.; Tsugawa, T.; Ogawa, T.; Saito, A. Climatological study of GPS total electron content variations caused by medium-scale traveling ionospheric disturbances. J. Geophys. Res. 2006, 111, A04306. [Google Scholar] [CrossRef]
- Chernigovskaya, M.A.; Shpynev, B.G.; Ratovsky, K.G. Meteorological effects of ionospheric disturbances from vertical radio sounding data. J. Atmos. Sol. Terr. Phys. 2015, 136, 235–243. [Google Scholar] [CrossRef]
- Chernigovskaya, M.A.; Shpynev, B.G.; Ratovsky, K.G.; Belinskaya, A.Y.; Stepanov, A.E.; Bychkov, V.V.; Grigorieva, S.A.; Panchenko, V.A.; Korenkova, N.A.; Mielich, J. Ionospheric response to winter stratosphere/lower mesosphere jet stream in the Northern Hemisphere as derived from vertical radio sounding data J. Atmos. Sol. Terr. Phys. J. Atmos. Sol. Terr. Phys. 2018, 180, 126–136. [Google Scholar] [CrossRef]
- Medvedev, A.V.; Ratovsky, K.G.; Tolstikov, M.V.; Alsatkin, S.S.; Scherbakov, A.A. Studying of the spatial–temporal structure of wavelike ionospheric disturbances on the base of Irkutsk incoherent scatter radar and digisonde data. J. Atmos. Sol. Terr. Phys. 2013, 105, 350–357. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Mylnikova, A.A.; Polyakova, A.S. Estimating the total electron content absolute value from the GPS/GLONASS data. Res. Phys. 2015, 5, 32–33. [Google Scholar] [CrossRef]
- Sivtseva, V.I.; Ammosov, P.P.; Gavrilyeva, G.A.; Koltovskoi, I.I.; Ammosova, A.M. Comparison between seasonal variations in tidal and internal gravity wave activity as derived from observations at Maimaga and Tiksi. Solar Terr. Phys. 2018, 4, 69–72. [Google Scholar] [CrossRef]
- Ammosov, P.P.; Gavrilyeva, G.A. Infrared Digital Spectrograph for Measuring Hydroxyl Rotational Temperature. Instrum. Exp. Tech. 2000, 43, 792–797. [Google Scholar] [CrossRef]
- Mies, F.H. Calculated Vibrational Transition Probabilities of OH(X2Π). J. Mol. Spectrosc. 1974, 53, 150–180. [Google Scholar] [CrossRef]
- Semenov, A.I.; Bakanas, V.V.; Perminov, V.I.; Zheleznov, Y.A.; Khomich, V.Y. The near infrared spectrum of the emission of the nighttime upper atmosphere of the Earth. Geomagnetism Aeronomy 2002, 42, 390–397. [Google Scholar]
- Perminov, V.I.; Semenov, A.I.; Shefov, N.N. On rotational temperature of the hydroxyl emission. Geomagnetism Aeronomy 2007, 47, 756–763. [Google Scholar] [CrossRef]
- Baker, D.J.; Stair, A.T. Rocket measurements of the altitude distributions of the hydroxyl airglow. Phys. Scripta 1988, 37, 611–622. [Google Scholar] [CrossRef]
- Von Savigny, C.; McDade, I.C.; Eichmann, K.-U.; Burrows, J.P. On the dependence of the OHMeinel emission altitude on vibrational level: SCIAMACHY observations and model simulations. Atmos. Chem. Phys. 2012, 12, 8813–8828. [Google Scholar] [CrossRef] [Green Version]
- Perminov, V.I.; Semenov, A.I.; Medvedeva, I.V.; Pertsev, N.N. Temperature Variations in the Mesopause Region According to the Hydroxyl-Emission Observations at Midlatitudes. Geomagnetism Aeronomy 2014, 54, 230–240. [Google Scholar] [CrossRef]
- Perminov, V.I.; Semenov, A.I.; Medvedeva, I.V.; Zheleznov, Y.A. Variability of mesopause temperature from the hydroxyl airglow observations over midlatitudinal sites, Zvenigorod and Tory, Russia. Adv. Space Res. 2014, 54, 2511–2517. [Google Scholar] [CrossRef]
- Bittner, M.; Offermann, D.; Graef, H.-H.; Donner, M.; Hamilton, K. An 18-year time series of OH rotational temperatures and middle atmosphere decadal variations. J. Atmos. Sol. -Terr. Phys. 2002, 64, 1147–1166. [Google Scholar] [CrossRef]
- Offermann, D.; Gusev, O.; Donner, M.; Forbes, J.M.; Hagan, M.; Mlynczak, M.G.; Oberheide, J.; Preusse, P.; Schmidt, H.; Russell, J.M., III. Relative intensities of middle atmosphere waves. J. Geophys. Res. 2009, 114, D06110. [Google Scholar] [CrossRef]
- Chunchuzov, I.P. On possible generation mechanism for nonstationary mountain waves in the atmosphere. J. Atmos. Sci. 1994, 15, 2196–2206. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.L.; Waters, J.W. Satellite observations of atmospheric variances: A possible indication of gravity waves. Geophys. Res. Lett. 1996, 23, 3631–3634. [Google Scholar] [CrossRef]
- Whiteway, J.A.; Duck, T.J.; Donovan, D.P.; Bird, J.C.; Pal, S.R.; Carswell, A.I. Measurements of gravity wave activity within and around the Arctic stratospheric vortex. Geophys. Res. Lett. 1997, 24, 1387–1390. [Google Scholar] [CrossRef] [Green Version]
- Gerrard, A.J.; Bhattacharya, Y.; Thayer, J.P. Observations of in-situ generated gravity waves during a stratospheric temperature enhancement (STE) event. Atmos. Chem. Phys. 2011, 11, 11913–11917. [Google Scholar] [CrossRef] [Green Version]
- Shpynev, B.G.; Churilov, S.M.; Chernigovskaya, M.A. Generation of waves by jet-stream instabilities in winter polar stratosphere/mesosphere. J. Atmos. Sol. -Terr. Phys. 2015, 136, 201–215. [Google Scholar] [CrossRef]
- Shpynev, B.G.; Khabituev, D.S.; Chernigovskaya, M.A.; Zorkal'tseva, O.S. Role of winter jet stream in the middle atmosphere energy balance. J. Atmos. Sol. Terr. Phys. 2019, 188, 1–10. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Yasyukevich, A.S.; Chernigovskaya, M.A.; Mylnikova, A.A.; Shpynev, B.G.; Khabituev, D.S. Seasonal and helio-geomagnetic activity pattern of the ionospheric variability over Russia’s Eastern Siberia and Far East region from the GPS/GLONASS data. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium—Spring (PIERS), St. Petersburg, Russia, 22–25 May 2017; pp. 2015–2022. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasyukevich, A.; Medvedeva, I.; Sivtseva, V.; Chernigovskaya, M.; Ammosov, P.; Gavrilyeva, G. Strong Interrelation between the Short-Term Variability in the Ionosphere, Upper Mesosphere, and Winter Polar Stratosphere. Remote Sens. 2020, 12, 1588. https://doi.org/10.3390/rs12101588
Yasyukevich A, Medvedeva I, Sivtseva V, Chernigovskaya M, Ammosov P, Gavrilyeva G. Strong Interrelation between the Short-Term Variability in the Ionosphere, Upper Mesosphere, and Winter Polar Stratosphere. Remote Sensing. 2020; 12(10):1588. https://doi.org/10.3390/rs12101588
Chicago/Turabian StyleYasyukevich, Anna, Irina Medvedeva, Vera Sivtseva, Marina Chernigovskaya, Petr Ammosov, and Galina Gavrilyeva. 2020. "Strong Interrelation between the Short-Term Variability in the Ionosphere, Upper Mesosphere, and Winter Polar Stratosphere" Remote Sensing 12, no. 10: 1588. https://doi.org/10.3390/rs12101588
APA StyleYasyukevich, A., Medvedeva, I., Sivtseva, V., Chernigovskaya, M., Ammosov, P., & Gavrilyeva, G. (2020). Strong Interrelation between the Short-Term Variability in the Ionosphere, Upper Mesosphere, and Winter Polar Stratosphere. Remote Sensing, 12(10), 1588. https://doi.org/10.3390/rs12101588