3.1. The gaPCA Algorithm
In the context of an increased interest in alternative and optimized PCA-based methods, we aimed at developing a novel algorithm focused on retaining more information by giving credit to the points located at the extremes of the distribution of the data, which are often ignored by the canonical PCA. Hence, gaPCA is a novel method that aims at approximating the principal components of a multidimensional dataset by estimating the direction of the principal components by the direction given by the points separated by the maximum distance of the dataset (the extremities of the distribution).
In the canonical PCA method, the principal components are given by the directions where the data varies the most and are obtained by computing the eigenvectors of the covariance matrix of the data. Because these eigenvectors are defined by the signal’s magnitude, they tend to neglect the information provided by the smaller objects which do not contribute much to the total signal’s variance.
Several different approaches have been proposed in order to overcome this shortcoming of the PCA and enhance the image information. Among them, the well-known projection pursuit techniques are focused on finding a set of linear projections that maximize a selected “projection index”. The work in [
26] defines this index as the information divergence from normality (the projection vectors located far from the normal distribution are the most interesting from the information point of view). In a similar manner, the method we propose gives credit to the elements at the extremes of the data distribution. The differences arise from the methodology of computing both the projection index and the projection vectors.
Among the specific features of the gaPCA method are an enhanced ability to discriminate smaller signals or objects from the background of the scene and the potential to accelerate computation time by using the latest High-Performance Computing architectures (the most intense computational task of gaPCA being distance computation, a task easily implemented on parallel architectures [
27]). From the computational perspective, gaPCA subscribes to the family of Projection Pursuit methods (because of the nature of its algorithm). These methods are known to be computationally expensive (especially for very large datasets). Moreover, most of them involve statistical computations, discrete functions and sorting operations that are not easily parallelized [
28,
29]. From this point of view, gaPCA has a computational advantage of being parallelizable and thus yielding decreased execution times (an important advantage in the case of a large hyperspectral dataset).
Unlike canonical PCA (for which the variance maximization objective function may imply discarding information coming from different data labels with similar features, where their separation is not on the highest variance) gaPCA retains more information from the dataset, especially related to smaller objects (or spectral classes). However, it is also true that like other Projection Pursuit (PP) methods, gaPCA beside being computationally expensive (especially for very large datasets) is also prone to noise interference (that is why a common practice in PP is to whiten the data, removing the noise [
26]). To illustrate our method, for the experiments, we did not perform any kind of whitening on the data prior to the method computation.
The gaPCA method was designed to obtain an orthonormal transform (for similarity with the standard PCA, for simplifying the computations and also for using the advantages of orthogonality). Each of the gaPCA components are mutually orthogonal, obtained iteratively, their ordering is the one produced by the algorithm. For proving the concept, we did not alter this order in any way. This means that different from the PCA approach, in gaPCA, the components are not ranked in terms of variance (or any other metric). A consequence of this is that the compressed information tends to be distributed among the components, and not concentrated in the first few like in the standard PCA.
The initial step of gaPCA consists of normalizing the input dataset, by subtracting the mean. Given a set of
n-dimensional points,
=
, the mean
is computed and subtracted.
The first gaPCA principal component is computed as the vector
that connects the two points:
, separated by the maximum Euclidean distance:
where
stands for the Euclidean distance.
The second principal component vector is computed as the difference between the two projections of the original elements in
onto the hyperplane
, determined by the normal vector
and containing
, the origin:
with
denoting the dot product operator.
represents the projected original points, computed using the following formula:
Consequently, the i-th basis vector is computed by projecting onto the hyperplane , finding the maximum distance-separated projections and computing their difference, .
The gaPCA algorithm has two main iterative steps (each one repeated by the number of times given by the desired number of principal components):
the first step consists of seeking the projection vector defined by two points separated by the maximum distance and
the second step consists of reducing the dimension of the data by projecting it onto the subspace orthogonal to the previous projection.
For reconstructing the original data, the components scores
S (which are the projection of each point onto the principal components) are computed (similarly to the PCA) by multiplying the original mean-centered data by the matrix of (retained) projection vectors.
The original data can be reconstructed by multiplying the scores
S by the transposed principal components matrix and adding the mean.
Algorithm 1 contains the pseudocode for the gaPCA method.
| Algorithm 1: gaPCA. |
![Remotesensing 12 01698 i001]() |
Algorithm 2 contains the pseudocode for the method that computes all the Euclidean distances between each point of a matrix
P.
| Algorithm 2: computeMaximumDistance. |
![Remotesensing 12 01698 i002]() |
Algorithm 3 contains the pseudocode for the method that computes the Euclidean projections of each point of matrix
P, on the hyperplane determined by the normal vector
v and containing the mean point of the dataset
.
| Algorithm 3: computeProjectionsHyperplane. |
![Remotesensing 12 01698 i003]() |
The first step, as mentioned above, is computing the two points and from the dataset that are separated by the maximum Euclidean distance. This is accomplished by computing the Euclidean distances between each pair of points in and returning the two corresponding points separated by the maximum distance. The first principal component is then computed as the vector obtained by subtracting the two values in the dataset = – . The mean of the datasets is computed next, and will be used as a reference for determining the hyperplanes in the next steps.
For each subsequent principal component that is determined (from the total number of k given as a parameter to the method), first the current dataset () is projected onto a hyperplane determined by the previous computed component and the point taken as reference . Once the projections are obtained, the algorithm proceeds to compute the furthest two points in dataset, which are consequently used for computing the i-th principal component ().
Figure 1 and
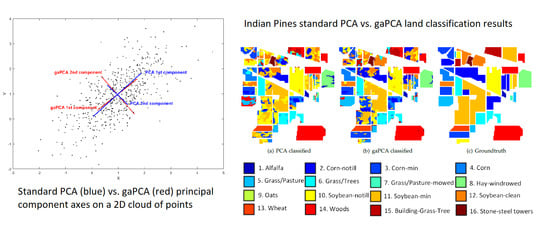
Figure 2 illustrate the graphical comparison between gaPCA and standard PCA when computing the principal components on a set of randomly generated bidimensional points normally distributed. In both figures, the original points are depicted as black dots; the red lines represent the gaPCA principal components of the points, while the blue lines are the standard principal components. In
Figure 1, the longer red line connects the two furthest points of the cloud of points (
and
, separated by the maximum distance of all the distances computed between all the points) and represents the first gaPCA component (
). The shorter red line is orthogonal on the first red line and provides the second gaPCA component (
).
Figure 2 depicts the normalized gaPCA vectors. One can notice the very high similarity of the red and blue lines, proving a close approximation of the standard PCA by the gaPCA method. The only visible difference is a small angle deviation.
In
Figure 3 three randomly-generated 2D points (in black), with the PCA represented with blue lines and gaPCA with red lines, for three values of the correlation coefficient:
0.5, 0.7 and 0.9, respectively, are shown. One may notice that for higher values of the correlation parameter, angle deviation decreases to very small values. This shows that the stronger the correlation of the variables, the better the approximation provided by gaPCA. On the other hand, when the dataset is weakly correlated, PCA’s direction of the axes is purely arbitrary (since there is no significant maximum variance axis).
3.2. Datasets
The first set of experimental data was gathered by AVIRIS sensor over the Indian Pines test site in the north-western Indiana and consists of 145 × 145 pixels and 224 (200 usable) spectral reflectance bands in the wavelength range 0.4–2.5 × 10
-6 m. The Indian Pines scene is a subset of a larger one and contains approximately 60 percent agriculture, and 30 percent forest or other natural perennial vegetation. There are two major dual-lane highways, a rail line, and some low density housing, other built structures, and smaller roads. The scene was taken in June and some of the crops present, corn, soybeans, are in early stages of growth with less than 5% coverage [
30].
Figure 4 displays an RGB image of the Indian Pines dataset.
The second data set used for experimental validation was the Pavia University data set, acquired by the ROSIS sensor during a flight campaign over Pavia in northern Italy. The scene containing the Pavia University has a number of 103 spectral bands. Pavia University is a 610 × 340 pixels image with a geometric resolution of 1.3 m. The image ground-truth differentiates nine classes [
31]. An RGB image of Pavia University is shown in
Figure 5.
The third set of experimental data was collected by the HYDICE sensor over a mall in Washington DC. It has 1280 × 307 pixels with 210 (191 usable) spectral bands in the range of 0.4–2.4
m. The spatial resolution is 2 m/pixel. An RGB image of the DC Mall is shown in
Figure 6.
The fourth set of experimental data used in this research was acquired by the airborne INTA-AHS instrument in the framework of the European Space Agency (ESA) AGRISAR measurement campaign [
32]. The test site is the area of Durable Environmental Multidisciplinary Monitoring Information Network (DEMMIN). This is a consolidated test site located in Mecklenburg–Western Pomerania, North-East Germany, which is based on a group of farms within a farming association, covering approximately 25,000 ha. The fields are very large in this area (in average, 200–250 ha). The main crops grown are wheat, barley, oilseed rape, maize, and sugar beet. The altitude range within the test site is around 50 m.
The AHS has 80 spectral channels available in the visible, shortwave infrared, and thermal infrared, with a pixel size of 5.2 m. For this research, the acquisition taken on the 6 June 2006, has been considered. At that time, five bands in the SWIR region became blind due to loose bonds in the detector array, so they were not used in this paper. An RGB image of the DEMMIN test site taken by the AHS instrument, also showing the image crop used in our experiments is illustrated in
Figure 7.