Review: Deep Learning on 3D Point Clouds
Abstract
:1. Introduction
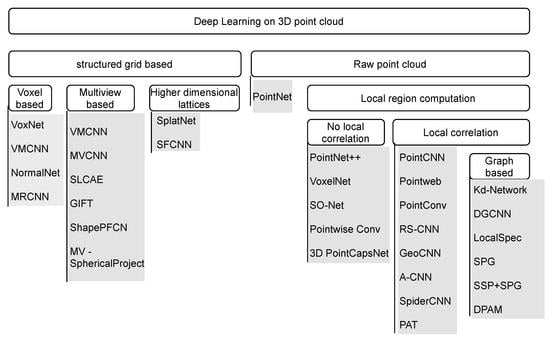
2. Methodology
3. Challenges of Deep Learning with Point Clouds
4. Structured Grid-Based Learning
4.1. Voxel-Based Approach
4.2. Multi-View-Based Approach
4.3. Higher-Dimensional Lattices
5. Deep Learning Directly with a Raw Point Cloud
5.1. PointNet
5.2. Approaches with Local Structure Computation
5.2.1. Approaches That Do Not Explore Local Correlation
5.2.2. Approaches That Explore Local Correlation
5.2.3. Graph-Based Approaches
5.3. Summary
6. Benchmark Datasets
6.1. 3D Model Datasets
6.1.1. ModelNet
6.1.2. ShapeNet
6.1.3. Augmenting ShapeNet
6.1.4. Shape2Motion
6.1.5. ScanObjectNN
6.2. Three-Dimensional Indoor Datasets
6.2.1. NYUDv2
6.2.2. SUN3D
6.2.3. S3DIS
6.2.4. SceneNN
6.2.5. ScanNet
6.2.6. Matterport3D
6.2.7. 3DMatch
6.2.8. Multisensor Indoor Mapping and Positioning Dataset
6.3. 3D Outdoor Datasets
6.3.1. KITTI
6.3.2. ASL Dataset
6.3.3. iQmulus
6.3.4. Oxford Robotcar
6.3.5. NCLT
6.3.6. Semantic3D
6.3.7. DBNet
6.3.8. NPM3D
6.3.9. Apollo
6.3.10. nuScenes
6.3.11. BLVD
6.3.12. Whu-TLS
7. Application of Deep Learning in 3D Vision Tasks
7.1. Classification
7.2. Segmentation
7.3. Object Detection
8. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D | One-dimensional |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| 4D | Four-dimensional |
| 5D | Five-dimensional |
| 6D | Six-dimensional |
| AFA | Adaptive feature adjustment |
| AR | Augmented reality |
| BCL | Bilateral convolutional layer |
| CAD | Computer-aided design |
| CNN | Convolutional neural network |
| D | Dimension |
| DGCNN | Dynamic graph convolutional neural network |
| DPAM | Dynamic points agglomeration module |
| ETH Zurich | Eidgenossische Technische Hochschule Zurich |
| FCN | Fully connected network |
| FPS | Farthest point sampling |
| fps | Frames per second |
| GPS | Global Positioning System |
| GSS | Gumbel subset sampling |
| IGN | Institut geographique national (National Geagraphic Institute) |
| IMU | Inertial measurement unit |
| INS | Inertial navigation system |
| KD network | k-dimensional network |
| KD tree | k-dimensional tree |
| KDE | Kernel density estimation |
| kNN | k-nearest neighbor |
| LiDAR | Light detection And ranging |
| MHA | Multi-head attention |
| MLP | Multi-layer perceptron |
| MLS | Mobile laser scanning |
| PAT | Point attention transformers |
| RGB | Red green blue |
| RGB-D | Red green blue–depth |
| SFCNN | Spherical fractal convolutional neural networks |
| SfM | Structure from motion |
| SLAM | Simultaneous localization and mapping |
| SLCAE | Stacked local convolutional autoencoder |
| SOM | Self organizing map |
| STN | Spatial transformer network |
| SVM | Support vector machine |
| VFE | Voxel feature encoding |
| VR | Virtual reality |
References
- Hillel, A.B.; Lerner, R.; Levi, D.; Raz, G. Recent progress in road and lane detection: A survey. Mach. Vis. Appl. 2014, 25, 727–745. [Google Scholar] [CrossRef]
- Pendleton, S.D.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, planning, control, and coordination for autonomous vehicles. Machines 2017, 5, 6. [Google Scholar] [CrossRef]
- Weingarten, J.W.; Gruener, G.; Siegwart, R. A state-of-the-art 3D sensor for robot navigation. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2155–2160. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981. [Google Scholar]
- Ayache, N. Artificial Vision for Mobile Robots: Stereo Vision and Multisensory Perception; Mit Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Liu, Y.; Dai, Q.; Xu, W. A point-cloud-based multiview stereo algorithm for free-viewpoint video. IEEE Trans. Vis. Comput. Graph. 2009, 16, 407–418. [Google Scholar]
- Fathi, H.; Brilakis, I. Automated sparse 3D point cloud generation of infrastructure using its distinctive visual features. Adv. Eng. Inform. 2011, 25, 760–770. [Google Scholar] [CrossRef]
- Livox Tech. Tele-15; Livox Tech: Shenzhen, China, 2020. [Google Scholar]
- Leica Geosystems. LEICA BLK360; Leica Geosystems: St. Gallen, Switzerland, 2016. [Google Scholar]
- Microsoft Corporation. Kinect V2 3D Scanner; Microsoft Corporation: Redmond, WA, USA, 2014. [Google Scholar]
- Schwarz, B. Mapping the world in 3D. Nat. Photonics 2010, 4, 429–430. [Google Scholar] [CrossRef]
- Tang, P.; Huber, D.; Akinci, B.; Lipman, R.; Lytle, A. Automatic reconstruction of as-built building information models from laser-scanned point clouds: A review of related techniques. Autom. Constr. 2010, 19, 829–843. [Google Scholar] [CrossRef]
- Wang, C.; Cho, Y.K.; Kim, C. Automatic BIM component extraction from point clouds of existing buildings for sustainability applications. Autom. Constr. 2015, 56, 1–13. [Google Scholar] [CrossRef]
- Pomerleau, F.; Colas, F.; Siegwart, R. A Review of Point Cloud Registration Algorithms for Mobile Robotics. Found. Trends Robot. 2015, 4, 1–104. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, B.; Feng, C.; Vallespi-Gonzalez, C.; Wellington, C. 3D Point Cloud Processing and Learning for Autonomous Driving. arXiv 2020, arXiv:2003.00601. [Google Scholar]
- Park, J.; Seo, D.; Ku, M.; Jung, I.; Jeong, C. Multiple 3D Object Tracking using ROI and Double Filtering for Augmented Reality. In Proceedings of the 2011 Fifth FTRA International Conference on Multimedia and Ubiquitous Engineering, Loutraki, Greece, 28–30 June 2011; pp. 317–322. [Google Scholar]
- Fabio, R. From point cloud to surface: The modeling and visualization problem. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, 34, W10. [Google Scholar]
- Johnson, A.E.; Hebert, M. Using Spin Images for Efficient Object Recognition in Cluttered 3D Scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Bhanu, B. 3D Free-Form Object Recognition in Range Images Using Local Surface Patches. In Proceedings of the 17th International Conference on Pattern Recognition (ICPR 2004), Cambridge, UK, 23–26 August 2004; pp. 136–139. [Google Scholar] [CrossRef]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3D object recognition. In Proceedings of the 12th IEEE International Conference on Computer Vision Workshops, ICCV Workshops 2009, Kyoto, Japan, 27 September–4 October 2009; pp. 689–696. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation (ICRA 2009), Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar] [CrossRef]
- Tombari, F.; Salti, S.; di Stefano, L. Unique shape context for 3d data description. In Proceedings of the ACM Workshop on 3D Object Retrieval (3DOR ’10), Firenze, Italy, 25 October 2010; Daoudi, M., Spagnuolo, M., Veltkamp, R.C., Eds.; pp. 57–62. [Google Scholar] [CrossRef]
- Hänsch, R.; Weber, T.; Hellwich, O. Comparison of 3d interest point detectors and descriptors for point cloud fusion. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 57. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E. Connectionist Learning Procedures. Artif. Intell. 1989, 40, 185–234. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G.E. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems 25: 26th Annual Conference on Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1106–1114. [Google Scholar]
- Ciresan, D.C.; Meier, U.; Schmidhuber, J. Multi-column deep neural networks for image classification. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv 2014, arXiv:1411.4038. [Google Scholar]
- Saito, S.; Li, T.; Li, H. Real-Time Facial Segmentation and Performance Capture from RGB Input. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Volume 9912, pp. 244–261. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. arXiv 2019, arXiv:1912.12033. [Google Scholar]
- Ioannidou, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. Deep Learning Advances in Computer Vision with 3D Data: A Survey. ACM Comput. Surv. 2017, 50, 20:1–20:38. [Google Scholar] [CrossRef]
- Liu, W.; Sun, J.; Li, W.; Hu, T.; Wang, P. Deep Learning on Point Clouds and Its Application: A Survey. Sensors 2019, 19, 4188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Y.; Sohel, F.; Bennamoun, M.; Wan, J.; Lu, M. A novel local surface feature for 3D object recognition under clutter and occlusion. Inf. Sci. 2015, 293, 196–213. [Google Scholar] [CrossRef]
- Nurunnabi, A.; West, G.; Belton, D. Outlier detection and robust normal-curvature estimation in mobile laser scanning 3D point cloud data. Pattern Recognit. 2015, 48, 1404–1419. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Dimitrov, A.; Golparvar-Fard, M. Segmentation of building point cloud models including detailed architectural/structural features and MEP systems. Autom. Constr. 2015, 51, 32–45. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018 (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; pp. 828–838. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef] [Green Version]
- Maturana, D.; Scherer, S. 3D Convolutional Neural Networks for landing zone detection from LiDAR. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2015), Seattle, WA, USA, 26–30 May 2015; pp. 3471–3478. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2015), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and Multi-view CNNs for Object Classification on 3D Data. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Cheng, M.; Sohel, F.; Bennamoun, M.; Li, J. NormalNet: A voxel-based CNN for 3D object classification and retrieval. Neurocomputing 2019, 323, 139–147. [Google Scholar] [CrossRef]
- Ghadai, S.; Lee, X.Y.; Balu, A.; Sarkar, S.; Krishnamurthy, A. Multi-Resolution 3D Convolutional Neural Networks for Object Recognition. arXiv 2018, arXiv:1805.12254. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2015), Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Riegler, G.; Ulusoy, A.O.; Geiger, A. OctNet: Learning Deep 3D Representations at High Resolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 6620–6629. [Google Scholar] [CrossRef] [Green Version]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Octree Generating Networks: Efficient Convolutional Architectures for High-resolution 3D Outputs. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2017), Venice, Italy, 22–29 October 2017; pp. 2107–2115. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E.G. Multi-view Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV 2015), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar] [CrossRef] [Green Version]
- Leng, B.; Guo, S.; Zhang, X.; Xiong, Z. 3D object retrieval with stacked local convolutional autoencoder. Signal Process. 2015, 112, 119–128. [Google Scholar] [CrossRef]
- Bai, S.; Bai, X.; Zhou, Z.; Zhang, Z.; Latecki, L.J. GIFT: A Real-Time and Scalable 3D Shape Search Engine. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 27–30 June 2016; pp. 5023–5032. [Google Scholar] [CrossRef] [Green Version]
- Kalogerakis, E.; Averkiou, M.; Maji, S.; Chaudhuri, S. 3D Shape Segmentation with Projective Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2017; pp. 6630–6639. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Huang, Q.; Ramani, K. 3D Object Classification via Spherical Projections. In Proceedings of the 2017 International Conference on 3D Vision, 3DV 2017, Qingdao, China, 10–12 October 2017; pp. 566–574. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Sun, J.; Zheng, Q. 3D Point Cloud Recognition Based on a Multi-View Convolutional Neural Network. Sensors 2018, 18, 3681. [Google Scholar] [CrossRef] [Green Version]
- Kanezaki, A.; Matsushita, Y.; Nishida, Y. RotationNet: Joint Object Categorization and Pose Estimation Using Multiviews From Unsupervised Viewpoints. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5010–5019. [Google Scholar]
- Su, H.; Jampani, V.; Sun, D.; Maji, S.; Kalogerakis, E.; Yang, M.; Kautz, J. SPLATNet: Sparse Lattice Networks for Point Cloud Processing. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2530–2539. [Google Scholar] [CrossRef] [Green Version]
- Rao, Y.; Lu, J.; Zhou, J. Spherical Fractal Convolutional Neural Networks for Point Cloud Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Oster, M.; Douglas, R.J.; Liu, S. Computation with Spikes in a Winner-Take-All Network. Neural Comput. 2009, 21, 2437–2465. [Google Scholar] [CrossRef] [Green Version]
- Xiang, C.; Qi, C.R.; Li, B. Generating 3D Adversarial Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Yang, J.; Zhang, Q.; Ni, B.; Li, L.; Liu, J.; Zhou, M.; Tian, Q. Modeling Point Clouds With Self-Attention and Gumbel Subset Sampling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. ScanNet: Richly-annotated 3D Reconstructions of Indoor Scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4490–4499. [Google Scholar] [CrossRef] [Green Version]
- Kohonen, T. The self-organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Li, J.; Chen, B.M.; Lee, G.H. SO-Net: Self-Organizing Network for Point Cloud Analysis. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 9397–9406. [Google Scholar] [CrossRef] [Green Version]
- Hua, B.; Tran, M.; Yeung, S. Pointwise Convolutional Neural Networks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 984–993. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Birdal, T.; Deng, H.; Tombari, F. 3D Point Capsule Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1009–1018. [Google Scholar]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing Between Capsules. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3856–3866. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. PointWeb: Enhancing Local Neighborhood Features for Point Cloud Processing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. PointConv: Deep Convolutional Networks on 3D Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-Shape Convolutional Neural Network for Point Cloud Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Lan, S.; Yu, R.; Yu, G.; Davis, L.S. Modeling Local Geometric Structure of 3D Point Clouds Using Geo-CNN. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Komarichev, A.; Zhong, Z.; Hua, J. A-CNN: Annularly Convolutional Neural Networks on Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. SpiderCNN: Deep Learning on Point Sets with Parameterized Convolutional Filters. In Proceedings of the Computer Vision—ECCV 2018—15th European Conference, Munich, Germany, 8–14 September 2018; Volume 11212, pp. 90–105. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Ni, B.; Li, C.; Yang, J.; Tian, Q. Dynamic Points Agglomeration for Hierarchical Point Sets Learning. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Klokov, R.; Lempitsky, V.S. Escape from Cells: Deep Kd-Networks for the Recognition of 3D Point Cloud Models. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2017), Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. arXiv 2018, arXiv:1801.07829. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Samari, B.; Siddiqi, K. Local Spectral Graph Convolution for Point Set Feature Learning. In Proceedings of the Computer Vision—ECCV 2018—15th European Conference, Munich, Germany, 8–14 September 2018; Volume 11208, pp. 56–71. [Google Scholar] [CrossRef] [Green Version]
- Han, W.; Wen, C.; Wang, C.; Li, Q.; Li, X. Forthcoming: Point2Node: Correlation Learning of Dynamic-Node for Point Cloud Feature Modeling. In Proceedings of the Conference on Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4558–4567. [Google Scholar]
- Landrieu, L.; Boussaha, M. Point Cloud Oversegmentation with Graph-Structured Deep Metric Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7440–7449. [Google Scholar]
- Wang, L.; Huang, Y.; Hou, Y.; Zhang, S.; Shan, J. Graph Attention Convolution for Point Cloud Semantic Segmentation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10296–10305. [Google Scholar]
- Liang, Z.; Yang, M.; Deng, L.; Wang, C.; Wang, B. Hierarchical Depthwise Graph Convolutional Neural Network for 3D Semantic Segmentation of Point Clouds. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8152–8158. [Google Scholar]
- Zhang, Z.; Hua, B.S.; Yeung, S.K. ShellNet: Efficient Point Cloud Convolutional Neural Networks Using Concentric Shells Statistics. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Chang, A.X.; Funkhouser, T.A.; Guibas, L.J.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H. ShapeNet: An Information-Rich 3D Model Repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active framework for region annotation in 3d shape collections. ACM Trans. Graph. (TOG) 2016, 35, 210. [Google Scholar] [CrossRef]
- Dai, A.; Qi, C.R.; Nießner, M. Shape Completion using 3D-Encoder-Predictor CNNs and Shape Synthesis. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Park, K.; Rematas, K.; Farhadi, A.; Seitz, S.M. PhotoShape: Photorealistic Materials for Large-Scale Shape Collections. ACM Trans. Graph. 2018, 37, 192. [Google Scholar] [CrossRef] [Green Version]
- Mo, K.; Zhu, S.; Chang, A.X.; Yi, L.; Tripathi, S.; Guibas, L.J.; Su, H. PartNet: A Large-Scale Benchmark for Fine-Grained and Hierarchical Part-Level 3D Object Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Xiang, Y.; Kim, W.; Chen, W.; Ji, J.; Choy, C.; Su, H.; Mottaghi, R.; Guibas, L.; Savarese, S. ObjectNet3D: A Large Scale Database for 3D Object Recognition. In Proceedings of the European Conference Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Wang, X.; Zhou, B.; Shi, Y.; Chen, X.; Zhao, Q.; Xu, K. Shape2Motion: Joint Analysis of Motion Parts and Attributes from 3D Shapes. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- 3D Warehouse. Available online: https://3dwarehouse.sketchup.com/ (accessed on 21 December 2019).
- Uy, M.A.; Pham, Q.H.; Hua, B.S.; Nguyen, D.T.; Yeung, S.K. Revisiting Point Cloud Classification: A New Benchmark Dataset and Classification Model on Real-World Data. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Hua, B.S.; Pham, Q.H.; Nguyen, D.T.; Tran, M.K.; Yu, L.F.; Yeung, S.K. SceneNN: A Scene Meshes Dataset with aNNotations. In Proceedings of the International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 746–760. [Google Scholar]
- Wasenmüller, O.; Stricker, D. Comparison of kinect v1 and v2 depth images in terms of accuracy and precision. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 34–45. [Google Scholar]
- Xiao, J.; Owens, A.; Torralba, A. Sun3d: A database of big spaces reconstructed using sfm and object labels. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 1625–1632. [Google Scholar]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.K.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar] [CrossRef]
- Fankhauser, P.; Bloesch, M.; Rodriguez, D.; Kaestner, R.; Hutter, M.; Siegwart, R. Kinect v2 for mobile robot navigation: Evaluation and modeling. In Proceedings of the 2015 International Conference on Advanced Robotics (ICAR), Istanbul, Turkey, 27–31 July 2015; pp. 388–394. [Google Scholar]
- Lachat, E.; Macher, H.; Mittet, M.; Landes, T.; Grussenmeyer, P. First experiences with Kinect v2 sensor for close range 3D modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 93. [Google Scholar] [CrossRef] [Green Version]
- Chang, A.; Dai, A.; Funkhouser, T.; Halber, M.; Niessner, M.; Savva, M.; Song, S.; Zeng, A.; Zhang, Y. Matterport3D: Learning from RGB-D Data in Indoor Environments. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Valentin, J.; Dai, A.; Nießner, M.; Kohli, P.; Torr, P.; Izadi, S.; Keskin, C. Learning to Navigate the Energy Landscape. arXiv 2016, arXiv:1603.05772. [Google Scholar]
- Shotton, J.; Glocker, B.; Zach, C.; Izadi, S.; Criminisi, A.; Fitzgibbon, A. Scene coordinate regression forests for camera relocalization in RGB-D images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2930–2937. [Google Scholar]
- De Deuge, M.; Quadros, A.; Hung, C.; Douillard, B. Unsupervised feature learning for classification of outdoor 3d scans. In Proceedings of the Australasian Conference on Robitics and Automation, Sydney, Australia, 2–4 December 2013; Volume 2, p. 1. [Google Scholar]
- Halber, M.; Funkhouser, T.A. Structured Global Registration of RGB-D Scans in Indoor Environments. arXiv 2016, arXiv:1607.08539. [Google Scholar]
- Wang, C.; Hou, S.; Wen, C.; Gong, Z.; Li, Q.; Sun, X.; Li, J. Semantic line framework-based indoor building modeling using backpacked laser scanning point cloud. ISPRS J. Photogramm. Remote Sens. 2018, 143, 150–166. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3642–3649. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef] [Green Version]
- Halterman, R.; Bruch, M. Velodyne HDL-64E lidar for unmanned surface vehicle obstacle detection. In Proceedings of the Unmanned Systems Technology XII. International Society for Optics and Photonics, Orlando, FL, USA, 6–9 April 2010; Volume 7692, p. 76920D. [Google Scholar]
- Glennie, C.; Lichti, D.D. Static calibration and analysis of the Velodyne HDL-64E S2 for high accuracy mobile scanning. Remote Sens. 2010, 2, 1610–1624. [Google Scholar] [CrossRef] [Green Version]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Stachniss, C.; Gall, J. SemanticKITTI: A Dataset for Semantic Scene Understanding of LiDAR Sequences. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Pomerleau, F.; Liu, M.; Colas, F.; Siegwart, R. Challenging data sets for point cloud registration algorithms. Int. J. Robot. Res. 2012, 31, 1705–1711. [Google Scholar] [CrossRef] [Green Version]
- Demski, P.; Mikulski, M.; Koteras, R. Characterization of Hokuyo UTM-30LX laser range finder for an autonomous mobile robot. In Advanced Technologies for Intelligent Systems of National Border Security; Springer: Berlin, Germany, 2013; pp. 143–153. [Google Scholar]
- Pouliot, N.; Richard, P.L.; Montambault, S. LineScout power line robot: Characterization of a UTM-30LX LIDAR system for obstacle detection. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 4327–4334. [Google Scholar]
- Brédif, M.; Vallet, B.; Serna, A.; Marcotegui, B.; Paparoditis, N. TerraMobilita/IQmulus Urban Point Cloud Classification Benchmark. In Proceedings of the Workshop on Processing Large Geospatial Data, Cardiff, UK, 8 July 2014. [Google Scholar]
- RIEGL Laser Measurement Systems. LMS-Q120i; RIEGL Laser Measurement Systems GmbH Riedenburgstraße 48: Horn, Austria, 2010. [Google Scholar]
- Maddern, W.; Pascoe, G.; Linegar, C.; Newman, P. 1 Year, 1000km: The Oxford RobotCar Dataset. Int. J. Robot. Res. 2017, 36, 3–15. [Google Scholar] [CrossRef]
- Csaba, G.; Somlyai, L.; Vámossy, Z. Mobil robot navigation using 2D LIDAR. In Proceedings of the 2018 IEEE 16th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Kosice, Slovakia, 7–10 February 2018; pp. 143–148. [Google Scholar]
- Carlevaris-Bianco, N.; Ushani, A.K.; Eustice, R.M. University of Michigan North Campus long-term vision and lidar dataset. Int. J. Robot. Res. 2016, 35, 1023–1035. [Google Scholar] [CrossRef]
- Chan, T.; Lichti, D.D.; Belton, D. Temporal analysis and automatic calibration of the Velodyne HDL-32E LiDAR system. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Jozkow, G.; Wieczorek, P.; Karpina, M.; Walicka, A.; Borkowski, A. Performance evaluation of sUAS equipped with Velodyne HDL-32e lidar sensor. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 171. [Google Scholar] [CrossRef] [Green Version]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. Semantic3d. net: A new large-scale point cloud classification benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar]
- Chen, Y.; Wang, J.; Li, J.; Lu, C.; Luo, Z.; Xue, H.; Wang, C. Lidar-video driving dataset: Learning driving policies effectively. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5870–5878. [Google Scholar]
- Roynard, X.; Deschaud, J.E.; Goulette, F. Paris-Lille-3D: A large and high-quality ground-truth urban point cloud dataset for automatic segmentation and classification. Int. J. Robot. Res. 2018, 37, 545–557. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Wang, P.; Zhou, D.; Zhu, R.; Guan, C.; Dai, Y.; Su, H.; Li, H.; Yang, R. Apollocar3d: A large 3d car instance understanding benchmark for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5452–5462. [Google Scholar]
- Lu, W.; Zhou, Y.; Wan, G.; Hou, S.; Song, S. L3-Net: Towards Learning Based LiDAR Localization for Autonomous Driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6389–6398. [Google Scholar]
- Sun, B.; Yeary, M.; Sigmarsson, H.H.; McDaniel, J.W. Fine Resolution Position Estimation Using the Kalman Filter. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019. [Google Scholar]
- Liu, W.; Shi, X.; Zhu, F.; Tao, X.; Wang, F. Quality analysis of multi-GNSS raw observations and a velocity-aided positioning approach based on smartphones. Adv. Space Res. 2019, 63, 2358–2377. [Google Scholar] [CrossRef]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A multimodal dataset for autonomous driving. arXiv 2019, arXiv:1903.11027. [Google Scholar]
- Xue, J.; Fang, J.; Li, T.; Zhang, B.; Zhang, P.; Ye, Z.; Dou, J. BLVD: Building A Large-scale 5D Semantics Benchmark for Autonomous Driving. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppäb, J. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Liang, F.; Huang, R.; Scherer, S. Hierarchical registration of unordered TLS point clouds based on binary shape context descriptor. ISPRS J. Photogramm. Remote Sens. 2018, 144, 61–79. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. FoldingNet: Point Cloud Auto-Encoder via Deep Grid Deformation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 206–215. [Google Scholar] [CrossRef] [Green Version]
- Rabbani, T.; van den Heuvel, F.; Vosselman, G. Segmentation of point clouds using smoothness constraints. In Proceedings of the ISPRS Commission V Symposium Vol. 35, Part 6: Image Engineering and Vision Metrology (ISPRS 2006), Dresden, Germany, 25–27 September 2006; Maas, H., Schneider, D., Eds.; Volume 35, pp. 248–253. [Google Scholar]
- Jagannathan, A.; Miller, E.L. Three-Dimensional Surface Mesh Segmentation Using Curvedness-Based Region Growing Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2195–2204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, J.; Wang, X.; Li, H. Interpolated Convolutional Networks for 3D Point Cloud Understanding. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Liu, Y.; Fan, B.; Meng, G.; Lu, J.; Xiang, S.; Pan, C. DensePoint: Learning Densely Contextual Representation for Efficient Point Cloud Processing. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Pham, Q.; Nguyen, D.T.; Hua, B.; Roig, G.; Yeung, S. JSIS3D: Joint Semantic-Instance Segmentation of 3D Point Clouds With Multi-Task Pointwise Networks and Multi-Value Conditional Random Fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, 16–20 June 2019; pp. 8827–8836. [Google Scholar]
- Yang, B.; Wang, J.; Clark, R.; Hu, Q.; Wang, S.; Markham, A.; Trigoni, N. Learning Object Bounding Boxes for 3D Instance Segmentation on Point Clouds. arXiv 2019, arXiv:1906.01140. [Google Scholar]
- Yi, L.; Zhao, W.; Wang, H.; Sung, M.; Guibas, L.J. GSPN: Generative Shape Proposal Network for 3D Instance Segmentation in Point Cloud. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3947–3956. [Google Scholar]
- Wang, W.; Yu, R.; Huang, Q.; Neumann, U. SGPN: Similarity Group Proposal Network for 3D Point Cloud Instance Segmentation. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2569–2578. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Liu, S.; Shen, X.; Shen, C.; Jia, J. Associatively Segmenting Instances and Semantics in Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2019), Long Beach, CA, USA, 16–20 June 2019; pp. 4096–4105. [Google Scholar]
- Engelmann, F.; Bokeloh, M.; Fathi, A.; Leibe, B.; Nießner, M. 3D-MPA: Multi Proposal Aggregation for 3D Semantic Instance Segmentation. arXiv 2020, arXiv:2003.13867. [Google Scholar]
- Lahoud, J.; Ghanem, B.; Oswald, M.R.; Pollefeys, M. 3D Instance Segmentation via Multi-Task Metric Learning. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 9255–9265. [Google Scholar]
- Narita, G.; Seno, T.; Ishikawa, T.; Kaji, Y. PanopticFusion: Online Volumetric Semantic Mapping at the Level of Stuff and Things. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4205–4212. [Google Scholar]
- Liang, Z.; Yang, M.; Wang, C. 3D Graph Embedding Learning with a Structure-aware Loss Function for Point Cloud Semantic Instance Segmentation. arXiv 2019, arXiv:1902.05247. [Google Scholar]
- Liu, C.; Furukawa, Y. MASC: Multi-scale Affinity with Sparse Convolution for 3D Instance Segmentation. arXiv 2019, arXiv:1902.04478. [Google Scholar]
- Hou, J.; Dai, A.; Nießner, M. 3D-SIS: 3D Semantic Instance Segmentation of RGB-D Scans. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4421–4430. [Google Scholar]
- Elich, C.; Engelmann, F.; Schult, J.; Kontogianni, T.; Leibe, B. 3D-BEVIS: Birds-Eye-View Instance Segmentation. arXiv 2019, arXiv:1904.02199. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R.B. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, ICCV 2017, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Girshick, R.B.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2014), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar] [CrossRef] [Green Version]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.B.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems 2015, Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; pp. 91–99. [Google Scholar]
- Redmon, J.; Divvala, S.K.; Girshick, R.B.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar] [CrossRef] [Green Version]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 6517–6525. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.Z.; Posner, I. Voting for Voting in Online Point Cloud Object Detection. In Proceedings of the Robotics: Science and Systems XI, Sapienza University of Rome, Rome, Italy, 13–17 July 2015. [Google Scholar] [CrossRef]
- Engelcke, M.; Rao, D.; Wang, D.Z.; Tong, C.H.; Posner, I. Vote3Deep: Fast object detection in 3D point clouds using efficient convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA 2017), Singapore, 29 May–3 June 2017; pp. 1355–1361. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum PointNets for 3D Object Detection From RGB-D Data. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 918–927. [Google Scholar] [CrossRef] [Green Version]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection From Point Cloud. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L.J. Deep Hough Voting for 3D Object Detection in Point Clouds. arXiv 2019, arXiv:1904.09664. [Google Scholar]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. PointPillars: Fast Encoders for Object Detection From Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.E.; Fu, C.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Computer Vision—ECCV 2016—14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Volume 9905, pp. 21–37. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-view 3D Object Detection Network for Autonomous Driving. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 6526–6534. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.; Yang, B.; Wang, S.; Urtasun, R. Deep Continuous Fusion for Multi-sensor 3D Object Detection. In Proceedings of the Computer Vision—ECCV 2018—15th European Conference, Munich, Germany, 8–14 September 2018; Volume 11220, pp. 663–678. [Google Scholar] [CrossRef]
- Shin, K.; Kwon, Y.P.; Tomizuka, M. RoarNet: A Robust 3D Object Detection based on RegiOn Approximation Refinement. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV 2019), Paris, France, 9–12 June 2019; pp. 2510–2515. [Google Scholar] [CrossRef] [Green Version]
- Ku, J.; Mozifian, M.; Lee, J.; Harakeh, A.; Waslander, S.L. Joint 3D Proposal Generation and Object Detection from View Aggregation. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2018), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Liang, M.; Urtasun, R. HDNET: Exploiting HD Maps for 3D Object Detection. In Proceedings of the 2nd Annual Conference on Robot Learning (CoRL 2018), Zürich, Switzerland, 29–31 October 2018; Volume 87, pp. 146–155. [Google Scholar]
- Yang, B.; Luo, W.; Urtasun, R. PIXOR: Real-Time 3D Object Detection From Point Clouds. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7652–7660. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Mao, Y.; Li, B. SECOND: Sparsely Embedded Convolutional Detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [Green Version]
- Angelina Uy, M.; Hee Lee, G. PointNetVLAD: Deep Point Cloud Based Retrieval for Large-Scale Place Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Liu, Z.; Zhou, S.; Suo, C.; Yin, P.; Chen, W.; Wang, H.; Li, H.; Liu, Y.H. LPD-Net: 3D Point Cloud Learning for Large-Scale Place Recognition and Environment Analysis. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]










| Method | Sampling | Grouping | Mapping Function |
|---|---|---|---|
| PointNet [42] | - | - | MLP |
| PointNet++ [39] | Farthest point sampling | Radius-search | MLP |
| PointCNN [41] | Uniform/Random sampling | k-NN | MLP |
| So-Net [67] | SOM-Nodes | Radius-search | MLP |
| Pointwise Conv [68] | - | Radius-search | MLP |
| Kd-Network [78] | - | Tree based nodes | Affine transformations+ReLU |
| DGCNN [79] | - | k-NN | MLP |
| LocalSpec [80] | Farthest point sampling | k-NN | Spectral convolution + cluster pooling |
| SpiderCNN [76] | Uniform sampling | k-NN | Taylor expansion |
| R-S CNN [73] | Uniform sampling | Radius-nn | MLP |
| PointConv [72] | Uniform sampling | Radius-nn | MLP |
| PAT [63] | Gumbel subset sampling | k-NN | MLP |
| 3D-PointCapsNet [69] | - | - | MLP+Dynamic routing |
| A-CNN [75] | Uniform subsampling | k-NN | MLP+Density functions |
| ShellNet [86] | Random Sampling | Spherical Shells | 1D convolution |
| Model | Indoor | Outdoor | ||
|---|---|---|---|---|
| CAD | ModelNet (2015, cls), ShapeNet (2015, seg), Augmenting ShapeNet, Shape2Motion (2019, seg, mot) | |||
| RGB-D | ScanObjectNN (2019, cls) | NYUDv2 (2012, seg), SUN3D (2013, seg), S3DIS (2016, seg), SceneNN (2016, seg), ScanNet (2017, seg), Matterport3D (2017, seg), 3DMatch (2017, reg) | ||
| LiDAR | Terrestrial LiDAR scanning | Semantic3D (2017, seg) | ||
| Mobile LiDAR scanning | Multisensor Indoor Mapping and Positioning Dataset (2018, loc) | KITTI (2012, det, odo), Semantic KITTI (2019, seg), ASL Dataset (2012, reg), iQmulus (2014, seg), Oxford Robotcar (2017, aut), NCLT (2016, aut), DBNet (2018, dri),NPM3D (2017, seg), Apollo (2018, det, loc), nuScenes (2019, det, aut), BLVD (2019, det) Whu-TLS (2020, reg) | ||
| Dataset | Dataset Capacity | Classification Categories | Segmentation Categories | Object Detection Categories | |
|---|---|---|---|---|---|
| CAD | ModelNet [48] | CAD models | 40 | ||
| ShapeNet [87] | models | 3135 | |||
| Shape2Motion [94] | models | 45 | |||
| RGB-D | ScanObjectNN [96] | objects | 15 | ||
| NYUDv2 [98] | RGB-D images | ||||
| SUN3D [100] | 254 different spaces | ||||
| S3DIS [101] | Over points | 13 | |||
| SceneNN [97] | 101 indoor scenes | 40 | |||
| ScanNet [64] | Nearly RGB-D images | 17 | 20 | ||
| Matterport3D [104] | RGB-D images | ||||
| 3DMatch [105] | 62 indoor scenes | ||||
| LiDAR | Semantic3D [126] | Over 4 billion points | 8 | ||
| MIMP [110] | Over points | ||||
| KITTI odometyr [111] | 22 sequences | ||||
| Semantic KITTI [115] | 22 sequences | 28 | |||
| ASL Dataset [116] | 8 sequences | ||||
| iQmulus [119] | points | 50 | |||
| Oxford Robotcar [121] | 100 sequences | ||||
| NCLT [123] | 27 sequences | ||||
| DBNet [127] | km driving data | ||||
| NPM3D [128] | points | 50 | |||
| Apollo [129,130] | images | More than car instances | |||
| nuScenes [133] | driving scenes | 23 classes and 8 attributes | |||
| BLVD [134] | 654 video clips | 3D annotations | |||
| Whu-TLS [135] |
| Method | Score (%) |
|---|---|
| PointNet [42] | 83.7 |
| PointCNN [41] | 84.6 |
| So-Net [67] | 84.6 |
| PointConv [72] | 85.7 |
| Kd-Network [78] | 82.3 |
| DGCNN [79] | 85.2 |
| LocalSpec [80] | 85.4 |
| SpiderCNN [76] | 85.3 |
| R-S CNN [73] | 86.1 |
| A-CNN [75] | 86.1 |
| ShellNet [86] | 82.8 |
| InterpCNN [141] | 84.0 |
| DensePoint [142] | 84.2 |
| Method | Datasets | Measure | Score (%) |
|---|---|---|---|
| PointNet [42] | mIOU | 47.7 | |
| Pointwise Conv [68] | 56.1 | ||
| DGCNN [79] | 56.1 | ||
| PointCNN [41] | 65.4 | ||
| PAT [63] | 54.3 | ||
| ShellNet [86] | 66.8 | ||
| Point2Node [81] | S3DIS | 70.0 | |
| InterpCNN [141] | 66.7 | ||
| PointNet [42] | OA | 78.5 | |
| PointCNN [41] | 88.1 | ||
| DGCNN [79] | 84.1 | ||
| A-CNN [75] | 87.3 | ||
| JSIS3D [143] | 87.4 | ||
| PointNet++ [39] | mIOU | 55.7 | |
| PointNet [42] | 33.9 | ||
| PointConv [72] | 55.6 | ||
| PointCNN [41] | 45.8 | ||
| PointNet [42] | ScanNet | OA | 73.9 |
| PointCNN [41] | 85.1 | ||
| A-CNN [75] | 85.4 | ||
| LocalSpec [80] | 85.4 | ||
| PointNet++ [39] | 84.5 | ||
| ShellNet [86] | 85.2 | ||
| Point2Node [81] | 86.3 |
| Method | Avg AP 50% | Bath -Tub | Bed | Book -Shelf | Cabi -Net | Chair | Coun -Ter | Curt -Ain | Desk | Door | Picture | Refrig -Erator | Shower Curtain | Sink |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D-MPA [148] | 0.611 | 1.00 | 0.833 | 0.765 | 0.526 | 0.756 | 0.136 | 0.588 | 0.47 | 0.438 | 0.358 | 0.65 | 0.857 | 0.429 |
| MTML [149] | 0.549 | 1.00 | 0.807 | 0.588 | 0.327 | 0.647 | 0.004 | 0.815 | 0.18 | 0.418 | 0.182 | 0.445 | 1.00 | 0.442 |
| 3D-BoNet [144] | 0.488 | 1.00 | 0.672 | 0.59 | 0.301 | 0.484 | 0.098 | 0.62 | 0.306 | 0.341 | 0.125 | 0.434 | 0.796 | 0.402 |
| PanopticFusion-inst [150] | 0.478 | 0.667 | 0.712 | 0.595 | 0.259 | 0.55 | 0.00 | 0.613 | 0.175 | 0.25 | 0.437 | 0.411 | 0.857 | 0.485 |
| ResNet-backbone [151] | 0.459 | 1.00 | 0.737 | 0.159 | 0.259 | 0.587 | 0.138 | 0.475 | 0.217 | 0.416 | 0.128 | 0.315 | 0.714 | 0.411 |
| MASC [152] | 0.447 | 0.528 | 0.555 | 0.381 | 0.382 | 0.633 | 0.002 | 0.509 | 0.26 | 0.361 | 0.327 | 0.451 | 0.571 | 0.367 |
| 3D-SIS [153] | 0.382 | 1.00 | 0.432 | 0.245 | 0.19 | 0.577 | 0.013 | 0.263 | 0.033 | 0.32 | 0.075 | 0.422 | 0.857 | 0.117 |
| UNet-backbone [151] | 0.319 | 0.667 | 0.715 | 0.233 | 0.189 | 0.479 | 0.008 | 0.218 | 0.067 | 0.201 | 0.107 | 0.123 | 0.438 | 0.15 |
| R-PointNet [145] | 0.306 | 0.5 | 0.405 | 0.311 | 0.348 | 0.589 | 0.054 | 0.068 | 0.126 | 0.283 | 0.028 | 0.219 | 0.214 | 0.331 |
| 3D-BEVIS [154] | 0.248 | 0.667 | 0.566 | 0.076 | 0.035 | 0.394 | 0.027 | 0.035 | 0.098 | 0.099 | 0.025 | 0.098 | 0.375 | 0.126 |
| Seg-Cluster [146] | 0.215 | 0.37 | 0.337 | 0.285 | 0.105 | 0.325 | 0.025 | 0.282 | 0.085 | 0.105 | 0.007 | 0.079 | 0.317 | 0.114 |
| Sgpn_scannet [146] | 0.143 | 0.208 | 0.39 | 0.169 | 0.065 | 0.275 | 0.029 | 0.069 | 0.00 | 0.087 | 0.014 | 0.027 | 0.00 | 0.112 |
| MaskRCNN 2d->3d Proj [155] | 0.058 | 0.333 | 0.002 | 0.00 | 0.053 | 0.002 | 0.002 | 0.021 | 0.00 | 0.045 | 0.238 | 0.065 | 0.00 | 0.014 |
| Method | Modality | Speed (HZ) | mAP | Car | Pedestrian | Cyclist | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moderate | Easy | Moderate | Hard | Easy | Moderate | Hard | Easy | Moderate | Hard | |||
| MV3D [168] | LiDAR & Image | 2.8 | N/A | 86.02 | 76.9 | 68.49 | N/A | N/A | N/A | N/A | N/A | N/A |
| Cont-Fuse [169] | LiDAR & Image | 16.7 | N/A | 88.81 | 85.83 | 77.33 | N/A | N/A | N/A | N/A | N/A | N/A |
| Roarnet [170] | LiDAR & Image | 10 | N/A | 88.2 | 79.41 | 70.02 | N/A | N/A | N/A | N/A | N/A | N/A |
| AVOD-FPN [171] | LiDAR & Image | 10 | 64.11 | 88.53 | 83.79 | 77.9 | 58.75 | 51.05 | 47.54 | 68.09 | 57.48 | 50.77 |
| F-PointNet [163] | LiDAR & Image | 5.9 | 65.39 | 88.7 | 84 | 75.33 | 58.09 | 50.22 | 47.2 | 75.38 | 61.96 | 54.68 |
| HDNET [172] | LiDAR & Map | 20 | N/A | 89.14 | 86.57 | 78.32 | N/A | N/A | N/A | N/A | N/A | N/A |
| PIXOR++ [173] | LiDAR | 35 | N/A | 89.38 | 83.7 | 77.97 | N/A | N/A | N/A | N/A | N/A | N/A |
| VoxelNet [65] | LiDAR | 4.4 | 58.52 | 89.35 | 79.26 | 77.39 | 46.13 | 40.74 | 38.11 | 66.7 | 54.76 | 50.55 |
| SECOND [174] | LiDAR | 20 | 60.56 | 88.07 | 79.37 | 77.95 | 55.1 | 46.27 | 44.76 | 73.67 | 56.04 | 48.78 |
| PointRCNN [164] | LiDAR | N/A | N/A | 89.28 | 86.04 | 79.02 | N/A | N/A | N/A | N/A | N/A | N/A |
| PointPillars [166] | LiDAR | 62 | 66.19 | 88.35 | 86.1 | 79.83 | 58.66 | 50.23 | 47.19 | 79.14 | 62.25 | 56 |
| Method | Modality | Speed (HZ) | mAP | Car | Pedestrian | Cyclist | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moderate | Easy | Moderate | Hard | Easy | Moderate | Hard | Easy | Moderate | Hard | |||
| MV3D [168] | LiDAR & Image | 2.8 | N/A | 71.09 | 62.35 | 55.12 | N/A | N/A | N/A | N/A | N/A | N/A |
| Cont-Fuse [169] | LiDAR & Image | 16.7 | N/A | 82.54 | 66.22 | 64.04 | N/A | N/A | N/A | N/A | N/A | N/A |
| Roarnet [170] | LiDAR & Image | 10 | N/A | 83.71 | 73.04 | 59.16 | N/A | N/A | N/A | N/A | N/A | N/A |
| AVOD-FPN [171] | LiDAR & Image | 10 | 55.62 | 81.94 | 71.88 | 66.38 | 50.8 | 42.81 | 40.88 | 64 | 52.18 | 46.64 |
| F-PointNet [163] | LiDAR & Image | 5.9 | 57.35 | 81.2 | 70.39 | 62.19 | 51.21 | 44.89 | 40.23 | 71.96 | 56.77 | 50.39 |
| VoxelNet [65] | LiDAR | 4.4 | 49.05 | 77.47 | 65.11 | 57.73 | 39.48 | 33.69 | 31.5 | 61.22 | 48.36 | 44.37 |
| SECOND [174] | LiDAR | 20 | 56.69 | 83.13 | 73.66 | 66.2 | 51.07 | 42.56 | 37.29 | 70.51 | 53.85 | 46.9 |
| PointRCNN [164] | LiDAR | N/A | N/A | 84.32 | 75.42 | 67.86 | N/A | N/A | N/A | N/A | N/A | N/A |
| PointPillars [166] | LiDAR | 62 | 59.2 | 79.05 | 74.99 | 68.3 | 52.08 | 43.53 | 41.49 | 75.78 | 59.07 | 52.92 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on 3D Point Clouds. Remote Sens. 2020, 12, 1729. https://doi.org/10.3390/rs12111729
Bello SA, Yu S, Wang C, Adam JM, Li J. Review: Deep Learning on 3D Point Clouds. Remote Sensing. 2020; 12(11):1729. https://doi.org/10.3390/rs12111729
Chicago/Turabian StyleBello, Saifullahi Aminu, Shangshu Yu, Cheng Wang, Jibril Muhmmad Adam, and Jonathan Li. 2020. "Review: Deep Learning on 3D Point Clouds" Remote Sensing 12, no. 11: 1729. https://doi.org/10.3390/rs12111729
APA StyleBello, S. A., Yu, S., Wang, C., Adam, J. M., & Li, J. (2020). Review: Deep Learning on 3D Point Clouds. Remote Sensing, 12(11), 1729. https://doi.org/10.3390/rs12111729