Spatio-Temporal Variability of Phytoplankton Primary Production in Baltic Lakes Using Sentinel-3 OLCI Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Satellite Data
2.3. The Primary Production (PP) Model
- The total lake PPint (PPlake, mg C h−1) for the entire lake. As all available images with ≥50% of the valid lake pixels were used in the study, PPlake was calculated by summarizing the available pixel values of PPint, and then the average of the available pixels of a given day was taken to substitute all of the missing surface-area pixels.
- The average areal PPint of the lake (PPaver, mg C m−2 h−1) was taken as the average of the PPlake over the surface area of the lake. For this parameter we also calculated the standard deviation (±) over the study period (April–October).
- The daily PPlake (PPlake,day, mg C d−1) was calculated by multiplying PPlake, the photoperiod (in h) of a given day, and the coefficient of 0.75 to take into account a daily light curve.
- The average daily areal PPint for the entire lake (PPday, mg C m−2 d−1) was taken as the average of the PPlake,day over the surface area of the lake.
- The monthly average PPday (PPday,aver, mg C m−2 d−1) was taken as the average of the PPday during one month.
- The monthly productivity estimates of the entire lake (PPmonth, Gg C month−1) were taken as the sums of PPlake,day for each month during the study period. If the PPlake,day value was missing due to the absence of overpass of the satellite or cloudy conditions, then inter- or extrapolation was used to calculate missing the PPlake,day value.
- The annual productivity estimates of the entire lake (PPyear, Gg C year−1) were taken as the sums of PPmonth during April–October 2018. We assumed that the PP during the rest of the months during 2018 is zero or close to zero due to ice and snow cover and not significant for the annual estimation of PP. Besides, there were no cloud-, ice-, or snow-free images available for the studied area from January to March, and November to December 2018.
- The annual average daily areal productivity (PPyear,aver, mg C m−2 d−1) was calculated by dividing PPyear by the number of days in a year and the surface area of the lake.
2.4. Input Parameters of the PP Model
2.4.1. Chlorophyll-a Concentration (Chl a)
2.4.2. The Underwater Light Diffuse Attenuation Coefficient (Kd,PAR)
2.4.3. Incident Planar Downwelling Irradiance (qPAR)
3. Results
3.1. Spatial Variability of PP
3.1.1. Lake Razna
3.1.2. Lake Lubans
3.1.3. Lake Võrtsjärv
3.1.4. Lake Burtnieks
3.2. Temporal Variability of the PP
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hamilton, T.L.; Corman, J.R.; Havig, J.R. Carbon and nitrogen recycling during cyanoHABs in dreissenid-invaded and non-invaded US midwestern lakes and reservoirs. Hydrobiologia 2020, 847, 939–965. [Google Scholar] [CrossRef] [Green Version]
- Huttunen, J.T.; Alm, J.; Liikanen, A.; Juutinen, S.; Larmola, T.; Hammar, T.; Silvola, J.; Martikainen, P.J. Fluxes of methane, carbon dioxide and nitrous oxide in boreal lakes and potential anthropogenic effects on the aquatic greenhouse gas emissions. Chemosphere 2003, 52, 609–621. [Google Scholar] [CrossRef]
- Cole, J.J.; Prairie, Y.T.; Caraco, N.F.; McDowell, W.H.; Tranvik, L.J.; Striegl, R.G.; Duarte, C.M.; Kortelainen, P.; Downing, J.A.; Middelburg, J.J.; et al. Plumbing the Global Carbon Cycle: Integrating Inland Waters into the Terrestrial Carbon Budget. Ecosystems 2007, 10, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Sanches, L.F.; Guenet, B.; Marinho, C.C.; Barros, N.; de Assis Esteves, F. Global regulation of methane emission from natural lakes. Sci. Rep. 2019, 9, 255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Tranvik, L.J.; Downing, J.A.; Cotner, J.B.; Loiselle, S.A.; Striegl, R.G.; Ballatore, T.J.; Dillon, P.; Finlay, K.; Fortino, K.; Knoll, L.B.; et al. Lakes and reservoirs as regulators of carbon cycling and climate. Limnol. Oceanogr. 2009, 54, 2298–2314. [Google Scholar] [CrossRef] [Green Version]
- Klaus, M.; Seekell, D.A.; Lidberg, W.; Karlsson, J. Evaluations of Climate and Land Management Effects on Lake Carbon Cycling Need to Account for Temporal Variability in CO2 Concentrations. Global Biogeochem. Cycles 2019, 33, 243–265. [Google Scholar] [CrossRef] [Green Version]
- Field, C.B. Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef] [Green Version]
- Marra, J. Vertical Mixing and Primary Production. In Primary Productivity in the Sea; Springer US: Boston, MA, USA, 1980; pp. 121–137. [Google Scholar]
- Kimmel, B.L.; Groeger, A.W. Factors controlling primary production in lakes and reservoirs: A perspective. Lake Reserv. Manag. 1984, 1, 277–281. [Google Scholar] [CrossRef]
- Downs, T.M.; Schallenberg, M.; Burns, C.W. Responses of lake phytoplankton to micronutrient enrichment: A study in two New Zealand lakes and an analysis of published data. Aquat. Sci. 2008, 70, 347–360. [Google Scholar] [CrossRef]
- Sterner, R.W. On the Phosphorus Limitation Paradigm for Lakes. Int. Rev. Hydrobiol. 2008, 93, 433–445. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems; Cambridge University Press: Cambridge, UK, 2010; ISBN 9781139168212. [Google Scholar]
- Pierson, D.C. Light and Primary Production in Lakes. In Encyclopedia of Earth Sciences Series; Springer Netherlands: Dordrecht, The Netherlands, 2012; pp. 485–492. [Google Scholar]
- Tanabe, Y.; Hori, M.; Mizuno, A.N.; Osono, T.; Uchida, M.; Kudoh, S.; Yamamuro, M. Light quality determines primary production in nutrient-poor small lakes. Sci. Rep. 2019, 9, 4639. [Google Scholar] [CrossRef] [Green Version]
- Steeman Nielsen, E. The use of radioactive carbon (14C) for measuring primary production in the sea. J. Du Cons. Int. Pour l’Exploration La Mer 1952, 18, 117–140. [Google Scholar] [CrossRef]
- Slawyk, G.; Collos, Y.; Auclair, J.-C. The use of the 13 C and 15 N isotopes for the simultaneous measurement of carbon and nitrogen turnover rates in marine phytoplankton1. Limnol. Oceanogr. 1977, 22, 925–932. [Google Scholar] [CrossRef]
- Cole, J.J.; Pace, M.L.; Carpenter, S.R.; Kitchell, J.F. Persistence of net heterotrophy in lakes during nutrient addition and food web manipulations. Limnol. Oceanogr. 2000, 45, 1718–1730. [Google Scholar] [CrossRef] [Green Version]
- Idrizaj, A.; Laas, A.; Anijalg, U.; Nõges, P. Horizontal differences in ecosystem metabolism of a large shallow lake. J. Hydrol. 2016, 535, 93–100. [Google Scholar] [CrossRef]
- Arst, H.; Nõges, P.; Nõges, T.; Kauer, T.; Arst, G.-E. Quantification of a Primary Production Model Using Two Versions of the Spectral Distribution of the Phytoplankton Absorption Coefficient. Environ. Model. Assess. 2012, 17, 431–440. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Oceanic Primary Production: Estimation by Remote Sensing at Local and Regional Scales. Science 1988, 241, 1613–1620. [Google Scholar] [CrossRef] [PubMed]
- Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Y.; Li, D.; Shi, K.; Zhang, Y. Temporal and Spatial Dynamics of Phytoplankton Primary Production in Lake Taihu Derived from MODIS Data. Remote Sens. 2017, 9, 195. [Google Scholar] [CrossRef]
- Boyer, J.N.; Kelble, C.R.; Ortner, P.B.; Rudnick, D.T. Phytoplankton bloom status: Chlorophyll a biomass as an indicator of water quality condition in the southern estuaries of Florida, USA. Ecol. Indic. 2009, 9, S56–S67. [Google Scholar] [CrossRef]
- Llewellyn, C.A. Phytoplankton community assemblage in the English Channel: A comparison using chlorophyll a derived from HPLC-CHEMTAX and carbon derived from microscopy cell counts. J. Plankton Res. 2004, 27, 103–119. [Google Scholar] [CrossRef] [Green Version]
- Yacobi, Y.Z.; Zohary, T. Carbon:chlorophyll a ratio, assimilation numbers and turnover times of Lake Kinneret phytoplankton. Hydrobiologia 2010, 639, 185–196. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Global Biogeochem. Cycles 2005, 19, 1–14. [Google Scholar] [CrossRef]
- Girdner, S.; Mack, J.; Buktenica, M. Impact of nutrients on photoacclimation of phytoplankton in an oligotrophic lake measured with long-term and high-frequency data: Implications for chlorophyll as an estimate of phytoplankton biomass. Hydrobiologia 2020, 847, 1817–1830. [Google Scholar] [CrossRef] [Green Version]
- Silsbe, G.M.; Behrenfeld, M.J.; Halsey, K.H.; Milligan, A.J.; Westberry, T.K. The CAFE model: A net production model for global ocean phytoplankton. Global Biogeochem. Cycles 2016, 30, 1756–1777. [Google Scholar] [CrossRef]
- Li, H.; Budd, J.W.; Green, S. Evaluation and Regional Optimization of Bio-optical Algorithms for Central Lake Superior. J. Great Lakes Res. 2004, 30, 443–458. [Google Scholar] [CrossRef]
- Lesht, B.M.; Barbiero, R.P.; Warren, G.J. A band-ratio algorithm for retrieving open-lake chlorophyll values from satellite observations of the Great Lakes. J. Great Lakes Res. 2013, 39, 138–152. [Google Scholar] [CrossRef]
- Warner, D.M.; Lesht, B.M. Relative importance of phosphorus, invasive mussels and climate for patterns in chlorophyll a and primary production in Lakes Michigan and Huron. Freshw. Biol. 2015, 60, 1029–1043. [Google Scholar] [CrossRef]
- Fahnenstiel, G.L.; Sayers, M.J.; Shuchman, R.A.; Yousef, F.; Pothoven, S.A. Lake-wide phytoplankton production and abundance in the Upper Great Lakes: 2010–2013. J. Great Lakes Res. 2016, 42, 619–629. [Google Scholar] [CrossRef]
- Yacobi, Y.Z. Temporal and vertical variation of chlorophyll a concentration, phytoplankton photosynthetic activity and light attenuation in Lake Kinneret: Possibilities and limitations for simulation by remote sensing. J. Plankton Res. 2006, 28, 725–736. [Google Scholar] [CrossRef] [Green Version]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef] [Green Version]
- Uudeberg, K. Optical Water Type Guided Approach to Estimate Water Quality in Inland and Coastal Waters. Ph.D. Thesis, University of Tartu, Tartu, Estonia, 2020. [Google Scholar]
- Kutser, T.; Verpoorter, C.; Paavel, B.; Tranvik, L.J. Estimating lake carbon fractions from remote sensing data. Remote Sens. Environ. 2015, 157, 138–146. [Google Scholar] [CrossRef]
- Giardino, C.; Bresciani, M.; Braga, F.; Cazzaniga, I.; De Keukelaere, L.; Knaeps, E.; Brando, V.E. Bio-optical Modeling of Total Suspended Solids. In Bio-Optical Modeling and Remote Sensing of Inland Waters; Elsevier: Amsterdam, The Netherlands, 2017; pp. 129–156. ISBN 9780128046548. [Google Scholar]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Kutser, T.; Koponen, S.; Kallio, K.Y.; Fincke, T.; Paavel, B. Bio-optical Modeling of Colored Dissolved Organic Matter. In Bio-Optical Modeling and Remote Sensing of Inland Waters; Elsevier: Amsterdam, The Netherlands, 2017; pp. 101–128. ISBN 9780128046548. [Google Scholar]
- Kauer, T.; Kutser, T.; Arst, H.; Danckaert, T.; Nõges, T. Modelling primary production in shallow well mixed lakes based on MERIS satellite data. Remote Sens. Environ. 2015, 163, 253–261. [Google Scholar] [CrossRef]
- Soomets, T.; Kutser, T.; Wüest, A.; Bouffard, D. Spatial and temporal changes of primary production in a deep peri-alpine lake. Inland Waters 2019, 9, 49–60. [Google Scholar] [CrossRef] [Green Version]
- ESA Sentinel-3 OLCI. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-olci (accessed on 18 June 2020).
- Eppley, R.; Stewart, E.; Abbott, M.; Owen, R. Estimating ocean production from satellite-derived chlorophyll: Insights from the Eastropac data set. In Proceedings of the International Symposium on Vertical Motion in the Equatorial Upper Ocean and its Effects Upon Living Resources and the AtmosphereOceanol, Paris, France, 6 May 1985; pp. 109–113. [Google Scholar]
- Behrenfeld, M.J.; Falkowski, P.G. A consumer’s guide to phytoplankton primary productivity models. Limnol. Oceanogr. 1997, 42, 1479–1491. [Google Scholar] [CrossRef] [Green Version]
- Tilstone, G.H.; Smyth, T.J.; Gowen, R.J.; Martinez-Vicente, V.; Groom, S.B. Inherent optical properties of the Irish Sea and their effect on satellite primary production algorithms. J. Plankton Res. 2005, 27, 1127–1148. [Google Scholar] [CrossRef]
- Joo, H.; Son, S.; Park, J.-W.; Kang, J.; Jeong, J.-Y.; Lee, C.; Kang, C.-K.; Lee, S. Long-Term Pattern of Primary Productivity in the East/Japan Sea Based on Ocean Color Data Derived from MODIS-Aqua. Remote Sens. 2016, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Carr, M.-E.; Friedrichs, M.A.M.; Schmeltz, M.; Noguchi Aita, M.; Antoine, D.; Arrigo, K.R.; Asanuma, I.; Aumont, O.; Barber, R.; Behrenfeld, M.; et al. A comparison of global estimates of marine primary production from ocean color. Deep Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 741–770. [Google Scholar] [CrossRef] [Green Version]
- Saba, V.S.; Friedrichs, M.A.M.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Behrenfeld, M.J.; Ciotti, A.M.; Dowell, M.; Hoepffner, N.; Hyde, K.J.W.; et al. An evaluation of ocean color model estimates of marine primary productivity in coastal and pelagic regions across the globe. Biogeosciences 2011, 8, 489–503. [Google Scholar] [CrossRef] [Green Version]
- Westberry, T.; Behrenfeld, M.J.; Siegel, D.A.; Boss, E. Carbon-based primary productivity modeling with vertically resolved photoacclimation. Global Biogeochem. Cycles 2008, 22, GB2024. [Google Scholar] [CrossRef] [Green Version]
- Gregg, W.W.; Rousseaux, C.S. Global ocean primary production trends in the modern ocean color satellite record (1998–2015). Environ. Res. Lett. 2019, 14, 124011. [Google Scholar] [CrossRef] [Green Version]
- Arst, H.; Nõges, T.; Nõges, P.; Paavel, B. In situ measurements and model calculations of primary production in turbid waters. Aquat. Biol. 2008, 3, 19–30. [Google Scholar] [CrossRef] [Green Version]
- LEGMC (State Limited Liability Company “Latvian Environment, Geology and Meteorology Centre”) National Monitoring Database. Available online: www.meteo.lv/fs/CKFinderJava/userfiles/ files/Par_centru/ES_projekti/Projekts_Udens_kvalitate/Assessment_on_data_availability_and_quality.do (accessed on 1 May 2020).
- Latvian Lakes Ezeri.Lv. Available online: www.ezeri.lv (accessed on 1 May 2020).
- Nõges, T.; Nõges, P.; Laugaste, R. Water level as the mediator between climate change and phytoplankton composition in a large shallow temperate lake. Hydrobiologia 2003, 506–509, 257–263. [Google Scholar] [CrossRef]
- Copernicus Online Data Access. Available online: Coda.eumetsat.int (accessed on 1 February 2019).
- Brockmann, C.; Doerffer, R.; Peters, M.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Zuhlke, M.; Fomferra, N.; Brockmann, C.; Peters, M.; Veci, L.; Malik, J.; Regner, P. SNAP (sentinel application platform) and the ESA sentinel 3 toolbox. In Proceedings of the Sentinel-3 for Science Workshop, Venice, Italy, 2–5 June 2015. [Google Scholar]
- Darecki, M.; Weeks, A.; Sagan, S.; Kowalczuk, P.; Kaczmarek, S. Optical characteristics of two contrasting Case 2 waters and their influence on remote sensing algorithms. Cont. Shelf Res. 2003, 23, 237–250. [Google Scholar] [CrossRef]
- Ligi, M.; Kutser, T.; Kallio, K.; Attila, J.; Koponen, S.; Paavel, B.; Soomets, T.; Reinart, A. Testing the performance of empirical remote sensing algorithms in the Baltic Sea waters with modelled and in situ reflectance data. Oceanologia 2017, 59, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.C.; Prezelin, B.B.; Bidigare, R.R.; Baker, K.S. Bio-optical modeling of photosynthetic production in coastal waters. Limnol. Oceanogr. 1989, 34, 1524–1544. [Google Scholar] [CrossRef]
- Uudeberg, K.; Ansko, I.; Põru, G.; Ansper, A.; Reinart, A. Using Optical Water Types to Monitor Changes in Optically Complex Inland and Coastal Waters. Remote Sens. 2019, 11, 2297. [Google Scholar] [CrossRef] [Green Version]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Brauns, A.; Zagars, M.; Kutser, T. Validation and Comparison of Water Quality Products in Baltic Lakes Using Sentinel-2 MSI and Sentinel-3 OLCI Data. Sensors 2020, 20, 742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alikas, K.; Kratzer, S.; Reinart, A.; Kauer, T.; Paavel, B. Robust remote sensing algorithms to derive the diffuse attenuation coefficient for lakes and coastal waters. Limnol. Oceanogr. Methods 2015, 13, 402–415. [Google Scholar] [CrossRef]
- Kuusk, J.; Kuusk, A. Hyperspectral radiometer for automated measurement of global and diffuse sky irradiance. J. Quant. Spectrosc. Radiat. Transf. 2018, 204, 272–280. [Google Scholar] [CrossRef]
- Nõges, T.; Arst, H.; Laas, A.; Kauer, T.; Nõges, P.; Toming, K. Reconstructed long-term time series of phytoplankton primary production of a large shallow temperate lake: The basis to assess the carbon balance and its climate sensitivity. Hydrobiologia 2011, 667, 205–222. [Google Scholar] [CrossRef]
- Kauer, T.; Arst, H.; Nõges, T.; Arst, G.-E. Development and application of a phytoplankton primary production model for well-mixed lakes. Proc. Est. Acad. Sci. 2013, 62, 267. [Google Scholar] [CrossRef]
- Vahtmäe, E.; Kutser, T.; Martin, G.; Kotta, J. Feasibility of hyperspectral remote sensing for mapping benthic macroalgal cover in turbid coastal waters—A Baltic Sea case study. Remote Sens. Environ. 2006. [Google Scholar] [CrossRef]
- Bulgarelli, B.; Kiselev, V.; Zibordi, G. Adjacency effects in satellite radiometric products from coastal waters: A theoretical analysis for the northern Adriatic Sea. Appl. Opt. 2017, 56, 854. [Google Scholar] [CrossRef] [PubMed]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Zagars, M.; Reinart, A.; Brauns, A.; Kutser, T. Comparison of Lake Optical Water Types Derived from Sentinel-2 and Sentinel-3. Remote Sens. 2019, 11, 2883. [Google Scholar] [CrossRef] [Green Version]
- Matthews, M.W.; Bernard, S.; Lain, L.R.; Griffith, D.; Odermatt, D.; Kutser, T. Understanding the Satellite Signal from Inland and Coastal Waters. In Earth Observations in Support of Global Water Quality Monitoring; Greb, S., Dekker, A., Binding, C.E., Eds.; International Ocean Color Coordinating Group: Dartmouth, NS, Canada, 2018; pp. 55–68. [Google Scholar]
- Yousef, F.; Charles Kerfoot, W.; Shuchman, R.; Fahnenstiel, G. Bio-optical properties and primary production of Lake Michigan: Insights from 13-years of SeaWiFS imagery. J. Great Lakes Res. 2014, 40, 317–324. [Google Scholar] [CrossRef]
- Shuchman, R.A.; Sayers, M.; Fahnenstiel, G.L.; Leshkevich, G. A model for determining satellite-derived primary productivity estimates for Lake Michigan. J. Great Lakes Res. 2013, 39, 46–54. [Google Scholar] [CrossRef]
- Bergamino, N.; Horion, S.; Stenuite, S.; Cornet, Y.; Loiselle, S.; Plisnier, P.D.; Descy, J.P. Spatio-temporal dynamics of phytoplankton and primary production in Lake Tanganyika using a MODIS based bio-optical time series. Remote Sens. Environ. 2010, 114, 772–780. [Google Scholar] [CrossRef]
- Luhtala, H.; Tolvanen, H. Optimizing the Use of Secchi Depth as a Proxy for Euphotic Depth in Coastal Waters: An Empirical Study from the Baltic Sea. ISPRS Int. J. Geo-Inf. 2013, 2, 1153–1168. [Google Scholar] [CrossRef]
- CIPEL (Commission International Pour la Protection des Eaux du Léman). Available online: http://www.cipel.org/ (accessed on 17 June 2020).
- Fee, E.J.; Shearer, J.A.; DeBruyn, E.R.; Schindler, E.U. Effects of Lake Size on Phytoplankton Photosynthesis. Can. J. Fish. Aquat. Sci. 1992, 49, 2445–2459. [Google Scholar] [CrossRef]








| Lake | Location | Area, km2 | Altitude, m | Mean Depth, m | Catchment Area, km2 | Trophic State |
|---|---|---|---|---|---|---|
| Razna | 56°19′N 27°28′E | 57.6 | 164 | 7.0 | 229 | mesotrophic |
| Lubans | 56°46′N 26°52′E | 80.7 | 90.0 | 1.6 | 2040 | eutrophic |
| Võrtsjärv | 58°16′N 26°02′E | 270 | 33.7 | 2.8 | 3374 | eutrophic |
| Burtnieks | 57°44′N 25°14′E | 40.2 | 47.0 | 2.4 | 2215 | eutrophic |
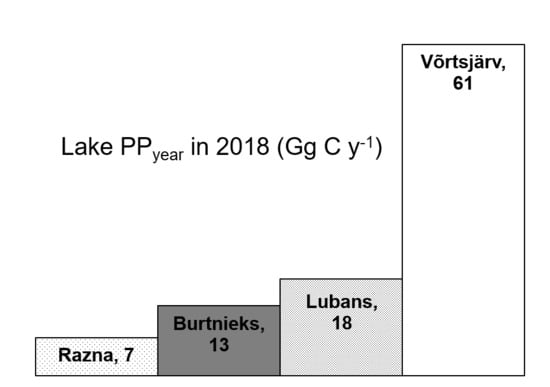
| Lake | S (km2) | PPyear (Gg C y−1) | PPyear,aver (mg C m−2 d−1) | Reference |
|---|---|---|---|---|
| Superior | 82,103 | 8100 | 274 | [4] |
| Huron | 59,590 | 5300 | 247 | [4] |
| Michigan | 58,030 | 6300 | 301 | [4] |
| Tanganyika | 32,900 | 7651 1 | 646 | [76] |
| Taihu | 2338 | 890 | 1094 | [23] |
| Geneva | 580 | 180 | 828 | [42] |
| Võrtsjärv | 270 | 61 | 622 | Current study |
| Lubans | 80.7 | 18 | 610 | Current study |
| Burtnieks | 40.2 | 13 | 887 | Current study |
| Razna | 57.6 | 7 | 333 | Current study |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soomets, T.; Uudeberg, K.; Kangro, K.; Jakovels, D.; Brauns, A.; Toming, K.; Zagars, M.; Kutser, T. Spatio-Temporal Variability of Phytoplankton Primary Production in Baltic Lakes Using Sentinel-3 OLCI Data. Remote Sens. 2020, 12, 2415. https://doi.org/10.3390/rs12152415
Soomets T, Uudeberg K, Kangro K, Jakovels D, Brauns A, Toming K, Zagars M, Kutser T. Spatio-Temporal Variability of Phytoplankton Primary Production in Baltic Lakes Using Sentinel-3 OLCI Data. Remote Sensing. 2020; 12(15):2415. https://doi.org/10.3390/rs12152415
Chicago/Turabian StyleSoomets, Tuuli, Kristi Uudeberg, Kersti Kangro, Dainis Jakovels, Agris Brauns, Kaire Toming, Matiss Zagars, and Tiit Kutser. 2020. "Spatio-Temporal Variability of Phytoplankton Primary Production in Baltic Lakes Using Sentinel-3 OLCI Data" Remote Sensing 12, no. 15: 2415. https://doi.org/10.3390/rs12152415
APA StyleSoomets, T., Uudeberg, K., Kangro, K., Jakovels, D., Brauns, A., Toming, K., Zagars, M., & Kutser, T. (2020). Spatio-Temporal Variability of Phytoplankton Primary Production in Baltic Lakes Using Sentinel-3 OLCI Data. Remote Sensing, 12(15), 2415. https://doi.org/10.3390/rs12152415