Estimating Fractional Snow Cover in Open Terrain from Sentinel-2 Using the Normalized Difference Snow Index

Abstract

Sentinel-2 provides the opportunity to map the snow cover at unprecedented spatial and temporal resolutions on a global scale. Here we calibrate and evaluate a simple empirical function to estimate the fractional snow cover (FSC) in open terrains using the normalized difference snow index (NDSI) from 20 m resolution Sentinel-2 images. The NDSI is computed from flat surface reflectance after masking cloud and snow-free areas. The NDSI–FSC function is calibrated using Pléiades very high-resolution images and evaluated using independent datasets including SPOT 6/7 satellite images, time lapse camera photographs, terrestrial lidar scans and crowd-sourced in situ measurements. The calibration results show that the FSC can be represented with a sigmoid-shaped function 0.5 × tanh(a × NDSI + b) + 0.5, where a = 2.65 and b = −1.42, yielding a root mean square error (RMSE) of 25%. Similar RMSE are obtained with different evaluation datasets with a high topographic variability. With this function, we estimate that the confidence interval on the FSC retrievals is 38% at the 95% confidence level.

1. Introduction

The Global Observing System for Climate listed snow cover as one of the 50 essential climate variables to be monitored by satellite remote sensing to support the work of the United Nations Framework Convention on Climate Change and the Intergovernmental Panel on Climate Change [1]. Among the many variables that can be used to characterize the snow cover, the snow cover area is probably the most straightforward to retrieve from space [2,3]. Yet, it is one of the most important as it serves as an input to address research questions in various fields including climate science, hydrology and ecology. The snow cover area is also important to support other societal benefit areas, such as water resource management, transportation and winter recreation. A user requirements survey by the Cryoland consortium showed that snow cover area products were ranked as the most important among a list of operationally available remotely sensed snow products by the respondents [4]. The respondents also emphasized the need for (i) short latency times in the product availability (shorter than 12 h); (ii) large spatial scale to cover entire mountain ranges like the Alps or even the whole of Europe; (iii) high spatial resolution down to 50 m resolution especially for road conditions and avalanche monitoring [4].

While the operational monitoring of the snow cover area at global scale has been achieved since the 2000s, using wide swath optical sensors, such as MODIS [2], the low spatial resolution of the products (typically 500 m) usually does not enable to address operational applications such as the above. Many scientific applications would also benefit from higher resolution information on the snow cover area. For instance, high resolution maps of the snow cover area were critical to explain the spatial diversity of plant communities in an alpine grassland [5,6]. High-resolution snow cover area is also useful in hydrology to reduce biases in the spatial distribution of the snow water equivalent through data assimilation [7], in particular in semi-arid mountain regions [8,9].

The Sentinel-2 mission, which images the land surface at high resolution with a 5-day revisit time and a global coverage offers the unique opportunity to bridge this gap [10,11]. As part of the Copernicus program, the Sentinel-2 mission is planned to run continuously for at least two decades. Based on the above, the Theia land data center in France has supported the deployment of an operational service to generate and distribute at no cost snow cover maps derived from Sentinel-2 (20 m resolution) and Landsat-8 (30 m resolution) [12]. However, this product only provides a binary description of the snow cover area in the pixel (snow or no-snow, hereafter referred to as SCA). The SCA mapping may be insufficient to characterize the snow distribution in areas where partially snow-covered (mixed) pixels are prevalent [13,14,15]. Using 0.5 m resolution satellite imagery, Selkowitz et al. [14] quantified the frequency of occurrence of mixed pixels over five dates at two study areas in the western U.S. Their results show that, in the study area with maritime climate, the fraction of mixed pixels at the typical Sentinel-2 resolution (20 m) is below 40%, whereas it can reach 80% in a more continental mountain area. Binarizing pixels in snow or no-snow in areas where mixed pixels are prevalent can introduce an error in the spatial integration of snow cover area—e.g., when the snow cover area is computed over a watershed [14].

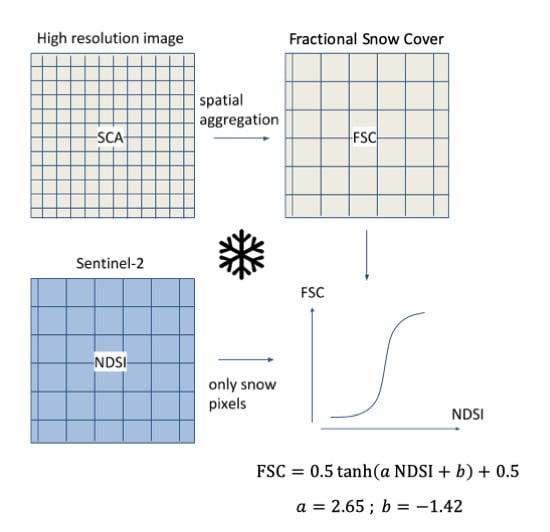
The Fractional Snow Cover (FSC)—i.e., the snow-covered fraction of the pixel area, naturally provides finer information than the binary SCA. However, it does not necessarily mean that it provides more accurate information. The estimation of the FSC from multi-spectral images is challenging due to the confounding effects of the snow, rocks and vegetation surfaces on the spectral signature of pixel reflectance [16]. Therefore, it is important to evaluate the accuracy of the retrieved FSC by comparing with independent observations to make sure that the gain in precision is worth the additional cost of computing and storage.

The spectral signature of a pixel can be modelled as a linear combination of the spectra of the pure surface materials, or endmembers thought to be present in it [17,18,19]. However, the spectral unmixing approach is challenging to use in an operational context: (i) it amounts to an ill-posed problem which requires a computationally intensive inversion step to estimate the relative abundance of each endmember; (ii) it requires prior knowledge of a collection of endmembers that covers the range of natural surfaces to be observed (geology, vegetation). Such requirements are hardly compatible with those of the users (timeliness, high resolution, large spatial scale).

Another option is to use the Normalized Difference Snow Index (NDSI) [20] as a means to retrieve the FSC through empirical regression. Previous studies involving lower-resolution sensors, such as MODIS and SPOT VEGETATION, have shown positive results using a linear function or a generalized logistic function to estimate the FSC from the NDSI [21,22]. A linear function was used by NASA in an operational context to generate the FSC from a collection of five MODIS surface reflectance products (MOD10A1.005 and MYD10A1.005) [23]. The current operational MODIS snow product does not provide for the FSC anymore but still provides the NDSI as a means to retrieve the FSC using custom equations [24]. A recent comparison of spectral unmixing and NDSI regression methods to estimate FSC with Sentinel-2 data showed that even an uncalibrated linear regression can yield nearly similar performance to the spectral unmixing [15]. This result was obtained despite the fact that endmembers for the spectral unmixing algorithm were chosen to match the characteristics of the study area (a high Arctic site). Apart from this study, to our best knowledge, there is no previous evaluation of the NDSI–FSC relationship from Sentinel-2 data.

Here, we aim at evaluating the NDSI regression method to generate FSC in the perspective of an operational service. Given the empirical nature of this approach and the lack of prior knowledge on this relationship, we endeavor to use a large amount of data covering a range of environments and seasons. We wish to evaluate if the error is stable across different sites and seasons.

We built this work upon our previous efforts that led to the implementation of the Theia snow collection. Theia snow products are currently generated by the LIS software version 1.5 [12]. The LIS algorithm already relies on the NDSI to determine the snow-covered pixels (hereinafter referred to as the LIS–SCA algorithm). The NDSI is computed from level-2A products—i.e., slope corrected surface reflectance images including a cloud and cloud shadow mask. The current configuration uses level-2A products generated by MAJA software. MAJA is an operational level-2A processor, which implements a multitemporal algorithm to estimate the aerosol optical thickness and make an accurate classification of cloud pixels [25,26]. The MAJA–LIS workflow was evaluated using in situ and remote sensing data [12]. The results showed that the snow cover area was accurately detected [12], and that the snow detection was more accurate than the Sen2Cor outputs [27].

We proceed as follows. First, we calibrate the function f which associates an FSC value to an NDSI value:

FSC = f(NDSI)

(1)

where f is a continuous, monotonically increasing function. The calibration is done using a set of very high-resolution satellite images, which provide accurate reference snow maps. Then, we evaluate this function in independent sites where we have reference data from various sources. Section 2 presents the data and methods used to perform such calibration and evaluation. In Section 3 we describe the results, and then discuss them in Section 4.

2. Data and Methods

2.1. Calibration

We used five clear-sky Pléiades tri-stereoscopic images to calibrate the NDSI–FSC function. This was done by generating accurate maps of the snow cover area at 2 m resolution from the Pléiades data, which were then resampled to obtain reference maps of the FSC at the same resolution of the NDSI (20 m) (Figure 1).

All selected Pléiades images were acquired over the same pilot site of 140 km² in the French Pyrenees after 2016 (Bassiès catchment, [28]). The elevation of the study area ranges between 730 and 2676 m a.s.l., with a contrasting topography and geology (Figure 2). In low-elevation regions, the vegetation is mainly formed by coniferous and deciduous trees; at middle elevations, between 1400 and 2000 m a.s.l., the surface is covered by grassland, rangeland and subalpine meadow; above 2000 m a.s.l., vegetation is scarce and the surface is made of bare crystalline rock (granite and granodiorite) or fluvio-glacial deposits, except in the north of the domain where metamorphosed limestone is found [29]. The images were acquired between February and May between 2016 and 2019 (

Table 1. Dates of the Pléiades and Sentinel-2 dataset pairs to calibrate and validate the NDSI–FSC relationship (dates are given in format year-month-day).

Pléiades	2016-04-11	2017-03-15	2018-02-15	2018-05-11	2019-03-26
Sentinel-2	2016-04-11	2017-03-14	2018-02-15	2018-05-11	2019-03-27

), providing information on different snow cover conditions, ranging from rather continuous snow cover in February to more spatially heterogeneous snow cover in May.

A single Pléiades bundle product consists of a 0.5 m resolution panchromatic image and a 2 m resolution multispectral image with four spectral bands (blue, green, red and near-infrared). First, a 2 m resolution digital elevation model (DEM) was produced from each bundle product using the panchromatic tri-stereo images [30]. Then, the nadir multispectral image of each triplet was projected onto the corresponding DEM to generate an orthorectified multispectral image at 2 m resolution in the UTM reference system. All Pléiades DEMs were aligned to the same reference DEM, which is known to have a horizontal offset of 3.0 m from the north and −0.8 m from the east (standard deviation 0.4 m) from control points obtained from an aerial orthophoto (see Table 2 in [28]). Hence this horizontal translation was applied to all Pléiades images before comparing them with Sentinel-2 to avoid introducing errors due to inaccurate geolocations of Pléiades data.

The resulting Pléiades multispectral orthoimages were used to generate the SCA maps of the five acquisitions with a pixel-based supervised classification. For each date, the few cloud pixels were manually delineated to restrict classification to cloud-free areas. The same procedure was applied to water bodies. Then we manually delineated about 15 homogeneous polygons of snow and no-snow surfaces (ground and vegetation) based on a color composite of the multispectral image which enhances the contrasts between rocks, water, vegetation and snow (NIR/red/green bands). These polygons were used to extract samples to train a random forest classifier with the Orfeo Toolbox [31]. The resulting 2 m SCA maps (Figure 3, middle panel) were then down-sampled to obtain 20 m FSC maps by computing the weighted average of all contributing pixels. If there was at least one no-data pixel among the contributing pixels then the FSC value was set to no data (Figure 3).

To evaluate the performance of the SCA classification in Pléiades images, we constructed an independent validation dataset. First, a mask of the non-forest area was extracted from the 2015 Copernicus Tree Cover Density (TCD) product at 20 m resolution (i.e., areas where TCD = 0). This mask was eroded using a disk of radius of 3 pixels to remove unidentified mixed pixels near the edges of the forest area. Then, 30 random points were created within this non-forest mask. A different person from the one who created the samples to train the classifier assigned the value “snow” or “no-snow” to each point for each date based on the visual inspection of the color composite of the multispectral image. This formed a set of 150 validation points that were used to compute performance metrics derived from the confusion matrix (accuracy, false-positive rate, false-negative rate, F1 score, kappa coefficient; see Section 2.2.4).

We used the 20 m Pléiades-derived FSC maps to calibrate the Sentinel-2 NDSI–FSC function. For each Pléiades map, we selected the Sentinel-2 image that was the closest in time (Table 1). The snow-covered pixels were determined with the LIS–SCA algorithm. The NDSI of these snow pixels was computed from the L2A product (flat surface reflectance). All images were mostly cloud-free (<5% cloud cover) over the study area, but the few visible cloud pixels were masked. All pixels with a positive TCD were excluded.

The Sentinel-2-derived NDSI and Pléiades-derived FSC datasets were paired on a pixel basis forming a list of approximately 6.4 × 10⁵ pairs which were randomly split in two subsets to perform the calibration and validation: 60% as a training dataset (for calibration) and 40% as a testing reference dataset (for validation). A nonlinear function with a sigmoid shape was chosen to represent the NDSI–FSC relationship because preliminary tests using an affine function were not satisfactory (not shown here). The following function was used:

FSC = ½ (tanh(a NDSI + b) + 1)

(2)

Figure 4 illustrates the shape of this function with a = 3 and b = −1. Parameters a and b were optimized using the root-mean-square error (RMSE) between the predicted FSC and the training FSC as the objective function to minimize. This optimization was done with the Nelder–Mead simplex algorithm as implemented in the SciPy library [32]. Once the NDSI–FSC relationship was calibrated, it was validated against the Pléiades testing dataset using standard metrics (Section 2.2.4).

2.2. Evaluation

2.2.1. Evaluation with Remote Sensing Data

We used several remote sensing datasets to evaluate the FSC algorithm (Figure 5). Here, remote sensing is taken in broad sense since the dataset was obtained from a variety of sensors, including close-range remote sensing instruments (terrestrial cameras and lidar scanner), aerial imagery and spaceborne sensors:

• SPOT: Five SPOT-6 and SPOT-7 maps of the snow cover area at 6 m resolution obtained by supervised classification [12]. Each SPOT scene covers a region of about 2900 km².
• Izas: A series of 758 SCA maps at 1 m resolution in the Izas catchment located in the Spanish Pyrenees. These snow maps were derived from a series of daily photographs taken between 2015 and 2019 by a terrestrial time-lapse camera (CC5MPX Campbell Sci.). The processing of the photographs to orthorectified SCA maps is described by Revuelto et al. [33]. The images cover an area of about 0.3 km².
• Weisssee: A series of nine SCA maps at 0.5 m resolution around the Weisssee Snow Research Site (Austria) [34]. These snow maps were derived from terrestrial laser scans presented by Fey et al. [35]. The discrimination of snow-covered and snow-free areas was based on surface reflectance and snow depth. The scans cover a region of about 0.9 km² with differing slopes and vegetation cover.
• CamSnow: A series of 351 FSC maps at 25 m resolution of the Aiguilles Rouges massif near Chamonix, France. These maps were derived from a series of daily photographs taken from 2016 to 2019 with a time-lapse camera installed in the Aiguille du Midi. The processing was done by TENEVIA, a start-up company specialized in the hydrometeorological monitoring of high mountain catchments. The images cover an area of about 50 km².
• We also obtained DISCHMEX data, a series of five SCA maps at 0.2 m resolution in the Dischma valley near Davos, Switzerland [36]. The snow cover area was retrieved from aerial ortho-images over a small region of about 0.1 km². However, we found that there were too few valid data in the DISCHMEX images to make an evaluation. This was due to the presence of many missing values in the original data and the fact that our resampling method considers that a resampled pixel becomes a no-data pixel if there is at least one no-data pixel in the contributing pixels (see below).

All the SCA data were resampled from their original projection to the projection system of the corresponding Sentinel-2 tile (WGS84 UTM 30N, 31N or 32N) at 20 m resolution by taking the average of the contributing pixels. As done in Section 2.2.1, if at least one pixel in the contributing pixels is a no-data pixel, the corresponding FSC pixel is also a no-data pixel to avoid introducing sampling biases.

Once an FSC product was matched with a Sentinel-2 acquisition, we selected the Sentinel-2 pixels marked as snow-covered by the LIS–SCA algorithm and computed their NDSI (as done in Section 2.2.1). The NDSI was then converted to FSC using the calibrated function obtained from Section 2.2.1. As a result, for each dataset, we obtained a list of reference FSC values that are collocated in space and time with a list of Sentinel-2 FSC values. This allowed a comparison at the Sentinel-2 pixel level, using the metrics defined in Section 2.2.4.

We handled the case where the FSC reference map can overlap two Sentinel-2 tiles (only SPOT). In this case, the SPOT product was cropped using the Sentinel-2 tiles extent and each portion was processed independently. In this process we made sure that the overlapping region between two Sentinel-2 tiles was not counted twice.

The comparison was not done at the pixel level for the CamSnow data for two reasons: (i) the CamSnow data already provide the FSC but at a somewhat coarser resolution (25 m instead of 20 m); (ii) a preliminary assessment of the CamSnow data revealed a non-rigid distortion of the projected FSC images, causing misalignment with Sentinel-2 data in the central part of the domain. This deformation is probably related to the projection of the image over a DEM, which is not perfectly corrected of small camera displacement (caused by extreme weather conditions) and cannot be easily corrected. Therefore, the CamSnow data were only used to evaluate the average FSC over a larger region corresponding to the full area of the CamSnow field of view. The latter method was also applied to Izas dataset (in addition to the pixel-level evaluation).

2.2.2. Evaluation Using Crowd-Sourced Data

Open Data Kit (ODK) Collect is an open source application for Android smartphones that replaces paper forms used in survey-based data gathering. For this study, a custom form for the ODK Collect application was made to allow the survey of the snow cover fraction around the observer. The ODK Aggregate application was installed on a server hosted by CESBIO to collect survey data. On 5 February 2020 a website was set up to explain the installation procedure and the measurement method (Figure 6). The announcement was spread using social media and mailing lists. The form and website were written in French. Consequently, most of the data were collected in the French Alps and Pyrenees. The participants were asked to estimate the snow-covered fraction of the surface in a disk of radius 10 m, centered at their position once the geolocation accuracy of their smartphone reached 5 m. The snow fraction value could be reported in the ODK form at a 10% interval between 0% and 100%.

The ODK FSC was directly compared to the FSC of the nearest pixel in the matching Sentinel-2 product, using the metrics defined in Section 2.2.4 below. Section 2.2.3 explains how this matching product was identified. Measurements made in forest areas were identified using the TCD product (i.e., where TCD > 0; Section 2.2.1) and removed from this analysis.

2.2.3. Sensitivity to the Temporal Collocation Method

Because Sentinel-2 acquisitions are not necessarily synchronized with other products, a reference FSC may have to be matched with a Sentinel-2 FSC product from a different date. In addition, the closest Sentinel-2 FSC product in time may not be the best choice in the case of cloudy conditions so that it might be useful to find the next closest product to increase the amount of evaluation data. However, the snow cover extent can change rapidly so it is necessary to bound the time search window that is used to match a reference product with a Sentinel-2 product. This is particularly important for dates before July 2017 (Sentinel-2B operation start date) when the revisit time of Sentinel-2 was only 10 days.

We evaluated the sensitivity of this time lag using the Izas collection due to its near daily temporal frequency over a multiyear period. We matched each Izas product with a Sentinel-2 product for a fixed time lag of 0 days. Then we repeated the operation with a 1-day increment for up to 12 days. An Izas product was ignored if it could not be matched with a Sentinel-2 product at the given time lag. Then we calculated the correlation between the Izas FSC and Sentinel-2 NDSI (as an indicator of the strength of the NDSI–FSC relationship). This gave us an estimation of the loss of consistency that should be expected by increasing the temporal search window between a reference product and a Sentinel-2 product.

We also tested the sensitivity of the selection criteria to match a reference product with a Sentinel-2 product. Indeed, within a given time window around the date of the reference products, one could find several Sentinel-2 products. We tested the following two options:

• Closest date: the Sentinel-2 product that is the closest in time to the FSC product is selected.
• Cleanest date: the Sentinel-2 product with the least cloud and no-data pixels is selected.

Both options were tested for different time windows from 0 to 4 days (for 0 days both methods are identical).

This issue is specific to FSC evaluation, where we must handle heterogeneous datasets with uneven temporal frequency such as ODK or CamSnow. This was not a problem in previous sections where Sentinel-2 FSC was compared either with daily snow depth measurements or a few Pléiades and SPOT images for which manual selection was possible.

2.2.4. Evaluation Metrics

For each type of high-resolution remote sensing, from all pairs of Sentinel-2 and reference data, we derive the following metrics: RMSE (root mean square error between the predicted and the observed FSC), mean error (mean of the differences between the predicted and the observed FSC), STD (standard deviation of the differences between the predicted and the observed FSC) and correlation (Pearson’s correlation coefficient between the predicted and the observed FSC).

3. Results

3.1. Calibration

Table 2. Evaluation of the Pléiades SCA maps with the validation points.

Validation Points	Pléiades SCA Maps
	Snow	No-Snow
snow	75	3
no-snow	4	63
Precision	0.95	0.95
Recall	0.96	0.94
F-score	0.95	0.95
Overall accuracy	0.95
Kappa	0.90

shows the confusion matrix between the Pléiades SCA maps at 2 m resolution and the 150 validation points. Among the 150 points, 5 were not classified due to the presence of clouds or because no decision was made by the analyst. The derived kappa and overall accuracy above 0.9 suggest that the Pléiades images have been correctly classified. This was expected from the visual evaluation of the Pléiades SCA maps which showed that the supervised random forest classifier allows an efficient classification of the snow areas given the high contrast with snow-free areas in the visible-NIR region of the spectra.

The calibration of the NDSI–FSC function with the Pléiades data returned the values a = 2.65 and b = −1.42 with an RMSE of 25% (Figure 7). In validation mode, the same RMSE was obtained, suggesting that the estimation of the error is robust (

Table 3. Validation of the predicted FSC against the testing dataset (Pléiades data).

Metric.	Value
Sample size	254664
RMSE	25%
Mean error	−0.9%
Standard deviation	24%
Correlation	0.60

).

3.2. Sensitivity to the Temporal Collocation Method

Figure 8 shows the decrease in the correlation coefficient as a function of the time lag between a Sentinel-2 product and reference product in the Izas dataset. The results suggest that the loss of consistency induced by a maximum time lag of 4 days should be low at least in the climatic context of the Pyrenees. From this analysis we chose a maximum time search window of 4 days to collocate Sentinel-2 FSC with reference FSC products.

Figure 9 illustrates the tradeoff between the “cleanest” and “closest” approaches in selecting the matching Sentinel-2 product. The number of pixels is higher with the cleanest method since this method selects the least cloudy image in a given time window, but the correlation coefficient is lower than the correlation coefficient of the closest method beyond 3 days, for the same reason as given in Figure 10. However, this analysis suggests that the difference between both methods is minimal. Given that the “closest” method is numerically more efficient, we kept this method with a time window of 4 days to perform the next analyses.

3.3. Evaluation with Remote Sensing Data

The results are presented for each set of remote sensing data used:

• SPOT: The results for SPOT are separated by date (

  Table 4. Pairs of SPOT and Sentinel-2 products used to perform the evaluation shown in Table 5 (dates are given in format year-month-day).

  Sentinel-2 Tiles	SPOT 2016-08-08	SPOT 2017-03-11	SPOT 2016-12-03	SPOT 2016-12-17	SPOT 2016-10-12
  T32TLR	2016-08-10	2017-03-11	2016-12-01	2016-12-18	2016-10-12
  T32TLQ	2016-08-10	2017-03-11	2016-12-01	2016-12-18
  T31TGK	2016-08-06	2017-03-11	2016-12-01	2016-12-14
  T31TGL	2016-08-06	2017-03-11	2016-12-01	2016-12-14	2016-10-12
  T31TGM					2016-10-12
  T32TLS					2016-10-12

  and

  Table 5. Evaluation of the Sentinel-2 FSC against the SPOT FSC (dates are given in format year-month-day).

  SPOT Date	2016-08-08	2016-10-12	2016-12-03	2016-12-17	2017-03-11
  Correlation	0.44	0.62	0.29	0.75	0.55
  STD	29%	33%	23%	21%	23%
  Mean error	−13%	−0.04%	−8.0%	−1.8%	−5.2%
  RMSE	31%	33%	25%	21%	24%

  ). The RMSE ranges between 21% and 31%, close to those obtained with the calibration–validation dataset (RMSE = 25%; Section 3.1). The absolute value of the mean error ranges between 13% and 0.04%, indicating that, despite a rather large dispersion, the FSC is not strongly biased.
• Izas: All available dates were merged as a single dataset. Despite the small size of the Izas study area, a large number of FSC values could be used thanks to the long duration of the time series and its near daily frequency (N = 4.5 × 10⁴). The results are in line with the previous evaluations with an RMSE of 21% and a mean error of −11% (

  Table 6. Evaluation of the Sentinel-2 FSC with Izas and Weisssee FSC (20 m pixel-based comparison), and CamSnow and Izas mean FSC (in percentage of the imaged area).

  Site	Izas	Weisssee	CamSnow	Izas
  Level	Pixel	Pixel	Area	Area
  Sample size	44,890	2492	181	437
  RMSE	21%	18%	20%	18%
  Mean error	−12%	−12%	3.5%	−10%
  STD	18%	13%	21%	16%
  Correlation	0.61	0.42	0.43	0.93

  ). The correlation coefficient of 0.61 indicates that the NDSI–FSC function provides a correct representation of the FSC in the Izas catchment.
• Weisssee: All available dates were also merged as a single dataset (Table 6). The correlation (0.42) is lower than that obtained with Izas data but the RMSE is improved (18%). This is because this dataset is skewed towards high FSC values, which tend to penalize the correlation with respect to the RMSE or the standard deviation (0.13).
• CamSnow: The comparison was done using the time series of average FSC over the study area (181 dates). Due the spatial aggregation which tends to decrease the random error, the performance of the FSC algorithm is acceptable with a correlation coefficient of 0.43, a RMSE of 20% and a mean error close to zero (−1.8%) (Table 6). However, it should be noted that the same type of evaluation using the mean spatial FSC was done with Izas data and the correlation coefficient is higher 0.94 (437 dates, Table 6). This suggests that the performance of CamSnow data may be affected by their inaccurate geometry and may not reflect the actual accuracy of the Sentinel-2 FSC (Section 2.2.2).

3.4. Evaluation with Crowd-Sourced in Situ Data

Table 7. Summary of the ODK Collect data obtained on March 15, 2020. In bold is the total number of collected ODK–FSC eventually used for the Sentinel-2 FSC evaluation.

Tile.	Available ODK Points	Accuracy ≤ 5 m	Accuracy ≤ 5 m and LIS–SCA Pixel = Snow
	TCD > 0	TCD > 0	TCD > 0
T31TDH	344	222	137
T30TYN	12	9	4
T31TGL	5	2	0
T31TCH	4	3	0
T32TLP	0	0	0
T31TGK	1	1	0
T32TLQ	0	0	0
T31TFL	0	0	0
T31TDG	0	0	0
T31TFK	0	0	0
TOTAL	366	237	141

summarizes the data that were contributed by the participants. After removing the data with a geolocation accuracy higher than 5 m, and data for which the LIS–SCA algorithm does not detect snow, we retained 337 FSC values. Among these 337 values, 141 were collected in areas with TCD > 0 (Table 7).

The comparison shows that there is a good agreement between the Sentinel-2 FSC and the ODK measurements with an RMSE that is again close to 25% (

Table 8. Evaluation of the Sentinel-2 FSC against the ODK data.

Metric	FSC
Sample size	337
RMSE	23%
Mean error	−7.2%
Standard deviation	21%
Correlation	0.67

, Figure 10).

4. Discussion

In both calibration or in evaluation sections, we obtained larger RMSE than previous studies using MODIS data to compute the FSC at coarser resolution for operational production. Salomonson and Appel [21] reported RMSE ranging between 4% and 10% for test sites over Alaska, Labrador, and Siberia by comparison with Landsat SCA products. These results were obtained with a linear function, which formed the basis of the MOD10A1.005 product algorithm. Using Landsat-8 SCF products, Rittger et al. [13] obtained an average RMSE of 10% with MODSCAG products. However, Rittger et al. [13] reported higher RMSE of 23% for MOD101A1.005, and Masson et al. [19] found larger RMSE for both MODSCAG and MOD10A1.005, ranging between 25–33%.

With Sentinel-2 data and a linear model of the NDSI, Aalstad et al. [15] obtained an RMSE of 7%, which is much lower than the RMSE obtained in this study. However, this was computed at 100 m resolution, and spatial aggregation from 20 m to 100 m is expected to reduce the error variance (see below). In addition, the model was only tested over a small region of 1.77 km² with a low topographic variability of (elevation range of 50 m). The same authors found that the error variance of FSC retrieved by spectral unmixing was larger for intermediate FSC and lower for high and low FSC residuals. Here we could not identify a similar behavior, although another form of heteroscedasticity is manifest in the Pléiades-derived FSC residuals from Section 3.1 (Figure 11). This dataset suggests that the error has a larger variability for low FSC retrievals.

Neglecting heteroscedasticity and assuming that the FSC residuals follow a gaussian distribution of zero mean and standard deviation σ, we can estimate the probability that a retrieval of SCF = 0 is significantly different than SCF = 1 at the pixel level. With the Normal inverse cumulative distribution function, we can estimate that σ should not exceed 61%, otherwise a retrieval of SCF = 0 would not be significantly different than SCF = 1 at the 5% confidence level. Here, we obtained an FSC model with a standard deviation of 24% in comparison with Pléiades validation data, and the standard deviation of the residuals did not exceed 30% except for the SPOT image of 12 October 2016 (33%). Therefore, the FSC model obtained in this study represents an improvement in accuracy over the binary SCA detection. Considering all datasets for which we could perform a pixel-wise comparison at 20 m resolution in this study, the median standard deviation of the residuals is 23%. Taking this value as the true standard deviation of the error distribution following a gaussian distribution, we can conclude that the confidence interval of an FSC retrieval is ±38% at the 95% confidence level.

This confidence interval is large, but it is expected to decrease by spatial averaging at a coarser resolution [37]. This can be observed in the case of Izas, since the standard deviation decreases from 18% to 16% by aggregation over the imaged area (Table 6). To further evaluate the effect of spatial resolution on the results, we also compared the FSC at coarser resolutions using the SPOT reference dataset. We selected SPOT because it has the largest coverage among all datasets and thus it provides a large amount of FSC values even at coarser resolutions. The FSC computed at 20 m resolution was averaged to 40 m, 80 m and 160 m resolution and the same performance metrics computed for all images. The results show increasing performances of the FSC model at coarser resolutions with a reduction in the RMSE from 25% to 21% and an increase in the correlation coefficient from 0.59 to 0.79 (

Table 9. Evaluation of the Sentinel-2 FSC against the SPOT validation dataset at different resolutions.

Resolution.	20 m	40 m	80 m	160 m
Correlation	0.59	0.67	0.75	0.79
STD	0.25	0.23	0.22	0.21
Mean error	−0.05	−0.04	−0.03	−0.01
RMSE	0.25	0.24	0.22	0.21

). This reduction in the FSC error may reflect the spatial misregistration of the Sentinel-2 level 1 data (geolocation accuracy is currently about 10 m (2σ) [11]), an issue which should have less impact at coarser resolution. However, it may also reflect the compensation of errors due to topographic variability. We analyzed the variations in the RMSE with the topographic slope in the case of the Bassiès area where there is a large range of slopes over a small area. The slopes were computed at 20 m resolution to match the FSC data and range from 0° to over 60°. Pixels with slopes above 50° were excluded as they represented a negligible fraction of the data. Figure 12 indicates that the RMSE tends to increase with the slope; however, the relationship remains weak, suggesting that the slope is a poor predictor of the error in this case. Further work is needed to characterize the spatial structure of the FSC error and potentially relate it to the topography and the sun geometry.

A large part of the evaluation was done using binary snow products as a reference which may create a bias in the fractional snow cover obtained by aggregation in a Sentinel-2 pixel due to the thresholding effect [13,14,15]. This effect was mitigated by using very-high resolution images both in calibration (2 m) and in evaluation (Izas 1 m, Weisssee 0.5 m) since the fraction of mixed snow pixels decreases at higher resolutions [14]. However, it may be more problematic with the SPOT data (6 m resolution). There is no such issue with the ODK dataset since the participants estimated the fractional snow cover directly. However, the ODK dataset suffers from other sources of uncertainties due to the difficulty to estimate FSC within a 10 m radius area in the field. Despite this limitation, the ODK data are well correlated (correlation coefficient: 0.67) with the FSC estimates, which encourages us to continue this experiment in the future with an improved user interface. The ODK data should be particularly useful to evaluate FSC in forested areas where remote sensing data are particularly scarce.

5. Conclusions

We studied the feasibility of retrieving FSC at 20 m resolution from Sentinel-2 NDSI. The main conclusions of this study are the following:

• The FSC can be estimated from the Sentinel-2 NDSI using a sigmoid-shaped function.
• The RMSE on the retrieved FSC is consistently estimated close to 25% from various reference datasets with a high topographic variability.
• With this function, we estimate that the confidence interval on the FSC retrievals is 38% at the 95% confidence level.
• The study presents limitations, the most important of which are described below:
• The evaluation focused on temperate mountain regions (Alps, Pyrenees).
• The evaluation focused on the snow cover above the tree line. The evaluation of the FSC in forest areas should be strengthened with measurements of the fractional snow cover data under trees.
• Sentinel-2 L1C products currently have a reported geolocation accuracy of about 10 m (2σ) [11], which could have a negative effect on the results presented here (i.e., the results could be better with an enhanced geolocation of Sentinel-2 images).
• This study focused on the snow detection but a major challenge in particular under operational constraint is the separation of the cloud from the snow cover. A major asset of the MAJA-LIS processing is the quality of the cloud mask in comparison with existing alternatives [26]. However, this should be further investigated in regions with extensive snow cover and frequent cloud coverage.

However, we argue that the most important step after this study is to focus the next evaluation on forest areas even if the retrieval algorithm should be modified to account for the obstruction of the ground by the trees [38]. Such an effort would allow a better characterization of Sentinel-2 capabilities to retrieve the snow cover fraction over large land masses with subarctic climate, whereas the present evaluation is more relevant for high-mountain regions.