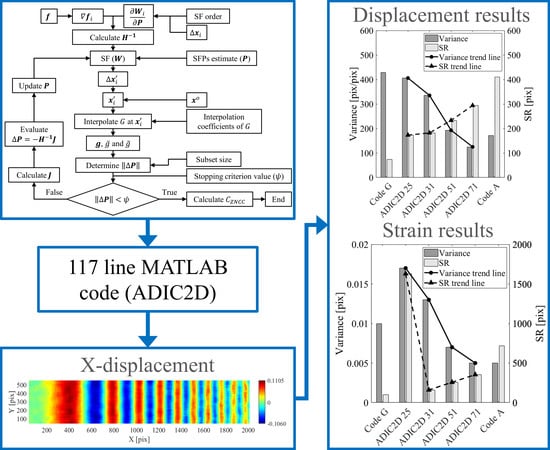
A 117 Line 2D Digital Image Correlation Code Written in MATLAB
Abstract
:1. Introduction
2. Framework Theory
2.1. Calibration
2.1.1. Homogeneous Coordinates
2.1.2. Pinhole Camera Model
2.1.3. Radial Distortion Model
2.1.4. Calibration Process
2.2. Correlation
2.2.1. Correlation Criterion
2.2.2. Shape Function
2.2.3. Interpolation
2.2.4. Gaussian Filtering
2.2.5. Optimisation Method
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| , | , |
| and . |
2.2.6. Stopping Criterion
2.3. Displacement Transformation
2.4. Strain Computation
3. Framework Implementation
3.1. ADIC2D Function
3.2. Correlation Implementation
3.2.1. ImgCorr Function
3.2.2. SubShapeExtract Function
3.2.3. SubCorr Function
3.2.4. SFExpressions Function
3.2.5. PCM Function
3.3. CSTrans Function
4. Validation
4.1. Quantifying Error
4.2. Samples 1–3
4.3. Sample 14
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Homogeneous scaling variable | |
| Window size for the Gaussian filter | |
| Skew of sensor coordinate system (intrinsic camera parameter) | |
| Translation applied to sensor coordinate system (intrinsic camera parameter) | |
| Zero-mean normalised sum of squared difference correlation criterion | |
| Zero-mean normalised cross correlation criterion | |
| Objective function of correlation | |
| Total projection error | |
| Reference image | |
| Reference subset | |
| Mean light intensity of reference subset | |
| Normalisation function of reference subset | |
| Light intensity gradient of the reference image | |
| Light intensity gradient of the reference subset | |
| Deformed image | |
| Investigated subset | |
| Mean light intensity of investigated subset | |
| Normalisation function of investigated subset | |
| Hessian of the optimisation equation | |
| Number of pixels per subset (counter is ) | |
| Jacobian of the optimisation equation | |
| Intrinsic camera parameters | |
| Radial distortion parameters | |
| Number of calibration images (counter is ) | |
| Number of calibration targets per calibration image (counter is ) | |
| Mean absolute error | |
| Function to populate a square matrix with the shape function parameters | |
| Stopping criterion value | |
| Shape function parameters | |
| Updated shape function parameters | |
| Iterative improvement estimate of the shape function parameters | |
| Number of subsets per an image (counter is ) | |
| Rotation matrix | |
| Root mean square error | |
| Calibration plate thickness | |
| Standard deviation of the Gaussian function for Gaussian filtering | |
| Variance (standard deviation of the absolute error) | |
| Time | |
| Translation vector | |
| Translation vector corrected for the thickness of the calibration plate | |
| Displacement in the x-direction in the distorted sensor coordinate system | |
| True displacement of subset in the x-direction in the distorted sensor coordinate system | |
| Calculated displacement of subset in the x-direction in the distorted sensor coordinate system | |
| Undistorted metric displacement in the x-direction in the world coordinate system | |
| , , , , | Derivatives of the x-direction displacement |
| Extrinsic camera parameters | |
| Displacement in the y-direction in the distorted sensor coordinate system | |
| True displacement of the subset in the y-direction in the distorted sensor coordinate system | |
| Calculated displacement of the subset in the y-direction in the distorted sensor coordinate system | |
| Undistorted metric displacement in the y-direction in the world coordinate system | |
| , , , , | Derivatives of the y-direction displacement |
| Shape function | |
| Jacobian of the shape function in terms of the shape function parameters for pixel | |
| Ideal world coordinates | |
| Ideal sensor coordinates | |
| Normalized ideal image coordinates | |
| Normalized distorted image coordinates | |
| Distorted sensor coordinates | |
| True location of the calibration targets in the distorted sensor coordinate system | |
| Location of the calibration targets in the distorted sensor coordinate system predicted by the camera model | |
| Centre of reference subset in the distorted sensor coordinate system | |
| Centre of reference subset in the undistorted sensor coordinate system | |
| Centre of investigated subset in the distorted sensor coordinate system | |
| Centre of investigated subset in the undistorted sensor coordinate system | |
| th pixel position of the reference subset in the distorted sensor coordinate system | |
| th pixel position of the investigated subset in the distorted sensor coordinate system | |
| Distance from the reference subset centre to th pixel position of reference subset | |
| Distance from the reference subset centre to th pixel position of investigated subset | |
| Undistorted reference subset position in the world coordinate system | |
| Undistorted investigated subset position in the world coordinate system | |
| Scaling of metric units to pixels (intrinsic camera parameter) | |
| Maximum distance of a pixel of the reference subset to the centre of the reference subset |
Appendix A
1 function ProcData=ADIC2D(FileNames,Mask,GaussFilt,StepSize,SubSize,
SubShape,SFOrder,RefStrat,StopCritVal,WorldCTs,ImgCTs,rho)
2 [~,ImNames]=cellfun(@fileparts,FileNames,’Uni’,0);
3 n=numel(FileNames);
4 [r,c]=size(im2double(imread(FileNames{1})));
5 [XosX,XosY]=meshgrid(((SubSize+1)/2+StepSize):StepSize:
(c-(SubSize+1)/2-1-StepSize),((SubSize+1)/2+StepSize):
StepSize:(r-(SubSize+1)/2-1-StepSize));
6 Xos=[XosX(:)’; XosY(:)’];
7 Xos=Xos(:,arrayfun(@(X,Y) min(min(Mask(Y-(SubSize-1)/2:Y+(SubSize-1)/2,X-(SubSize-1)/2:X+(SubSize-1)/2))),Xos(1,:),Xos(2,:))==1);
8 ProcData=struct(’ImgName’,ImNames,’ImgSize’,repmat({[r,c]},1,n), ’ImgFilt’,repmat({GaussFilt},1,n),’SubSize’,repmat({SubSize*ones([1,size(Xos,2)])},1,n),’SubShape’,repmat({repmat(SubShape,size(Xos,2),1)},1,n),’SFOrder’,repmat({repmat(SFOrder,size(Xos,2),1)},1,n),’Xos’,repmat({Xos},1,n),’P’,repmat({zeros([12,size(Xos,2)])},1,n),’C’,repmat({ones([1,size(Xos,2)])},1,n),’StopVal’,repmat({ones([1,size(Xos,2)])*StopCritVal},1,n),’Iter’,repmat({zeros([1,size(Xos,2)])},1,n));
9 ProcData=ImgCorr(n,ProcData,FileNames,RefStrat,StopCritVal); % Section 3.2.1
10 ProcData=CSTrans(n,ProcData,WorldCTs,ImgCTs,rho); % Section 3.3
1 function PD=ImgCorr(n,PD,ImNames,RefStrat,StopCritVal)
2 SubExtract=@(Mat,Xos,SubSize) Mat(Xos(2)-(SubSize-1)/2:Xos(2)+(SubSize-1)/2,Xos(1)-(SubSize-1)/2:Xos(1)+(SubSize-1)/2);
3 for d=2:n, tic; % outer loop
4 G=im2double(imread(ImNames{d}));
5 if all(PD(d).ImgFilt), G=imgaussfilt(G,PD(d).ImgFilt(1), ’FilterSize’,PD(d).ImgFilt(2)); end % Section 2.2.4
6 InterpCoef=griddedInterpolant({1:1:size(G,1),1:1:size(G,2)}, G,’spline’); % Section 2.2.3
7 if any([RefStrat==1,d==2])
8 F=im2double(imread(ImNames{d-1}));
9 if all(PD(d).ImgFilt), F=imgaussfilt(F,PD(d).ImgFilt(1), ’FilterSize’,PD(d).ImgFilt(2)); end % Section 2.2.4
10 [dFdx,dFdy]=imgradientxy(F,’prewitt’);
11 PD(d).Xos(1,:)=PD(d-1).Xos(1,:)+fix(PD(d-1).P(1,:));
12 PD(d).Xos(2,:)=PD(d-1).Xos(2,:)+fix(PD(d-1).P(7,:));
13 [PD(d).P(1,:),PD(d).P(7,:)]=arrayfun(@(XosX,XosY,SubSize) PCM(F,G,SubSize,XosX,XosY,SubExtract),PD(d).Xos(1,:),PD(d).Xos(2,:),PD(d).SubSize); % Section 3.2.5
14 else
15 PD(d).P=PD(d-1).P;
16 end
17 P=zeros(size(PD(d).P)); C=zeros(size(PD(d).C)); Iter=zeros(size(PD(d).C)); StopVal=ones(size(PD(d).C));
18 for q=1:size(PD(d).Xos,2) % inner loop (can be changed to parfor for parallel processing)
19 [f,dfdx,dfdy,dX,dY]=SubShapeExtract(PD(d).SubSize(q), PD(d).SubShape(q,:),PD(d).Xos(:,q),F,dFdx,dFdy,SubExtract); % Section 3.2.2
20 [P(:,q),C(q),Iter(q),StopVal(q)]=SubCorr(InterpCoef,f,dfdx, dfdy,PD(d).SubSize(q),PD(d).SFOrder(q),PD(d).Xos(:,q),dX,dY,PD(d).P(:,q),StopCritVal); % Section 3.2.3
21 end
22 PD(d).P=P; PD(d).C=C; PD(d).Iter=Iter; PD(d).StopVal=StopVal;
23 if rem(d-2,10)==0, fprintf(’Image/Total| Time (s) | CC (min) | CC (mean) | Iter (max) \n’); end
24 fprintf(’ %4.d/%4.d | %7.3f | %.6f | %.6f | %3.0f \n’,d,n,toc,min(PD(d).C),nanmean(PD(d).C),max(PD(d).Iter));
25 end
1 function [f,dfdx,dfdy,dX,dY]=SubShapeExtract(SubSize,SubShape,Xos,F,
dFdx,dFdy,SubExtract)
2 switch SubShape
3 case ’Square’
4 f(:)=reshape(SubExtract(F,Xos,SubSize),[SubSize*SubSize,1]);
5 dfdx(:)=reshape(SubExtract(dFdx,Xos,SubSize), [SubSize*SubSize,1]);
6 dfdy(:)=reshape(SubExtract(dFdy,Xos,SubSize), [SubSize*SubSize,1]);
7 [dX,dY]=meshgrid(-(SubSize-1)/2:(SubSize-1)/2, -(SubSize-1)/2:(SubSize-1)/2); dX=dX(:); dY=dY(:);
8 case ’Circle’
9 f=SubExtract(F,Xos,SubSize);
10 dfdx=SubExtract(dFdx,Xos,SubSize);
11 dfdy=SubExtract(dFdy,Xos,SubSize);
12 [dX,dY]=meshgrid(-(SubSize-1)/2:(SubSize-1)/2,-(SubSize-1)/2:(SubSize-1)/2); 13 mask_keep=sqrt(abs(dX).^2+abs(dY).^2)<=(SubSize/2-0.5);
14 f=f(mask_keep);
15 dfdx=dfdx(mask_keep); dfdy=dfdy(mask_keep);
16 dX=dX(mask_keep); dY=dY(mask_keep);
17 end
1 function [P,C,iter,StopVal]=SubCorr(InterpCoef,f,dfdx,dfdy,SubSize,
SFOrder,Xos,dX,dY,P,StopCritVal)
2 [W,dFdWdP,SFPVec2Mat,Mat2SFPVec,StopCrit]=SFExpressions(SFOrder); % Section 3.2.4
3 dfdWdP=dFdWdP(dX(:),dY(:),dfdx(:),dfdy(:));
4 Hinv=inv(dfdWdP’*dfdWdP); % inverse of Equation (20)
5 f_bar=mean(f(:)); f_tilde=sqrt(sum((f(:)-f_bar).^2));
6 flag=0; iter=0; dP=ones(size(P));
7 while flag==0
8 [dXY]=W(dX(:),dY(:),P); % Equation (14)
9 g=InterpCoef(Xos(2).*ones(size(dXY,1),1)+dXY(:,2), Xos(1).*ones(size(dXY,1),1)+dXY(:,1));
10 g_bar=mean(g(:)); g_tilde=sqrt(sum((g(:)-g_bar).^2));
11 StopVal=StopCrit(dP,(SubSize-1)/2); % Equation (23)
12 if any([StopVal<StopCritVal,iter>100])
13 flag=1;
14 C=1-sum(((f(:)-f_bar)/f_tilde-(g(:)-g_bar)/g_tilde).^2)/2; % Equation (11) substituted into Equation (13)
15 else
16 J=dfdWdP’*(f(:)-f_bar-f_tilde/g_tilde*(g(:)-g_bar)); % Summation of Equation (19)
17 dP([1:SFOrder*3+0^SFOrder 7:6+SFOrder*3+0^SFOrder])= -Hinv*J; % Equation (19)
18 P=Mat2SFPVec(SFPVec2Mat(P)/SFPVec2Mat(dP)); % Equation (21)
19 end
20 iter=iter+1;
21 end
1 function [W,dFdWdP,SFPVec2Mat,Mat2SFPVec,StopCrit]=
SFExpressions(SFOrder)
2 switch SFOrder
3 case 0 % Zero order SF
4 W=@(dX,dY,P) [P(1)+dX,P(7)+dY]; % Equation (14)
5 dFdWdP=@(dX,dY,dfdx,dfdy) [dfdx,dfdy];
6 SFPVec2Mat=@(P) reshape([1,0,0,0,1,0,P(1),P(7),1],[3,3]); % Equation (22)
7 Mat2SFPVec=@(W) [W(7),0,0,0,0,0,W(8),0,0,0,0,0];
8 StopCrit=@(dP,Zeta) sqrt(sum((dP’.*[1,0,0,0,0,0,1,0,0,0,0,0]) .^2)); % Equation (23)
9 case 1 % First order SF
10 W=@(dX,dY,P) [P(1)+P(3).*dY+dX.*(P(2)+1), P(7)+P(8).*dX+dY.*(P(9)+1)]; % Equation (14)
11 dFdWdP=@(dX,dY,dfdx,dfdy) [dfdx,dfdx.*dX,dfdx.*dY, dfdy,dfdy.*dX,dfdy.*dY];
12 SFPVec2Mat=@(P) reshape([P(2)+1,P(8),0,P(3),P(9)+1,0,P(1), P(7),1],[3,3]); % Equation (22)
13 Mat2SFPVec=@(W) [W(7),W(1)-1.0,W(4),0,0,0,W(8),W(2), W(5)-1.0,0,0,0];
14 StopCrit=@(dP,Zeta) sqrt(sum((dP’.*[1,Zeta,Zeta,0,0,0,1,Zeta, Zeta,0,0,0]).^2)); % Equation (23)
15 case 2 % Second order SF
16 W=@(dX,dY,P) [P(1)+P(3).*dY+P(4).*dX.^2.*(1/2)+P(6).*dY.^2.* (1/2)+dX.*(P(2)+1)+P(5).*dX.*dY,P(7)+P(8).*dX+P(10).*dX.^2.*(1/2)+P(12).*dY.^2.*(1/2)+dY.*(P(9)+1)+P(11).*dX.*dY]; % Equation (14)
17 dFdWdP=@(dX,dY,dfdx,dfdy) [dfdx,dfdx.*dX,dfdx.*dY, (dfdx.*dX.^2)/2,dfdx.*dX.*dY,(dfdx.*dY.^2)/2,dfdy,dfdy.*dX,dfdy.*dY,(dfdy.*dX.^2)/2,dfdy.*dX.*dY,(dfdy.*dY.^2)/2];
18 SFPVec2Mat=@(P) reshape([P(2)*2+P(1)*P(4)+P(2)^2+1, P(1)*P(10)*1/2+P(4)*P(7)*(1/2)+P(8)*(P(2)*2+2)*1/2,P(7)*P(10)+P(8)^2,P(4)*1/2,P(10)*1/2,0,P(1)*P(5)*2+P(3)*(P(2)*2+2),P(2)+P(9)+P(2)*P(9)+P(3)*P(8)+P(1)*P(11)+P(5)*P(7)+1,P(7)*P(11)*2.0+P(8)*(P(9)+1)*2,P(5),P(11),0,P(1)*P(6)+P(3)^2,P(1)*P(12)*1/2+P(6)*P(7)*1/2+P(3)*(P(9)+1),P(9)*2+P(7)*P(12)+P(9)^2+1,P(6)*1/2,P(12)*1/2,0,P(1)*(P(2)+1)*2,P(7)+P(1)*P(8)+P(2)*P(7),P(7)*P(8)*2,P(2)+1,P(8),0,P(1)*P(3)*2,P(1)+P(1)*P(9)+P(3)*P(7),P(7)*(P(9)+1)*2,P(3),P(9)+1,0,P(1)^2,P(1)*P(7),P(7)^2,P(1),P(7),1],[6,6]); % Equation (22)
19 Mat2SFPVec=@(W) [W(34),W(22)-1,W(28),W(4).*2,W(10),W(16).*2, W(35),W(23),W(29)-1,W(5).*2,W(11),W(17).*2];
20 StopCrit=@(dP,Zeta) sqrt(sum((dP’.*[1,Zeta,Zeta,0.5*Zeta, 0.5*Zeta,0.5*Zeta,1,Zeta,Zeta,0.5*Zeta,0.5*Zeta,0.5*Zeta]).^2)); % Equation (23)
21 end
1 function [u,v]=PCM(F,G,SubSize,XosX,XosY,SubExtract)
2 NCPS=(fft2(SubExtract(F,[XosX,XosY],SubSize)) .*conj(fft2(SubExtract(G,[XosX,XosY],SubSize))))./abs(fft2(SubExtract(F,[XosX,XosY],SubSize)).*conj(fft2(SubExtract(G,[XosX,XosY],SubSize))));
3 CC=abs(ifft2(NCPS));
4 [vid,uid]=find(CC==max(CC(:)));
5 IndShift=-ifftshift(-fix(SubSize/2):ceil(SubSize/2)-1);
6 u=IndShift(uid);
7 v=IndShift(vid);
1 function PD=CSTrans(n,PD,WorldCTs,ImgCTs,rho)
2 if WorldCTs~=0 | ImgCTs~=0
3 CamParams=estimateCameraParameters(ImgCTs,WorldCTs); % Section 2.1.4
4 else
5 CamParams=cameraParameters(’ImageSize’,PD(1).ImgSize, ’IntrinsicMatrix’,eye(3),’WorldPoints’,PD(1).Xos’,’RotationVectors’,[0,0,0],’TranslationVectors’,[0,0,0]);
6 WorldCTs=PD(1).Xos’; ImgCTs=PD(1).Xos’;
7 end
8 [R,T]=extrinsics(ImgCTs(:,:,end),WorldCTs,CamParams);
9 Tspec=T-[0,0,rho]*R; % Equation (6)
10 for d=1:n
11 Xds(1,:)=PD(d).Xos(1,:)+PD(d).P(1,:); % Equation (24)
12 Xds(2,:)=PD(d).Xos(2,:)+PD(d).P(7,:); % Equation (24)
13 PD(d).Xow=pointsToWorld(CamParams,R,Tspec, undistortPoints(PD(d).Xos’,CamParams))’;
14 Xdw=pointsToWorld(CamParams,R,Tspec, undistortPoints(Xds’,CamParams))’;
15 PD(d).Uw=Xdw-PD(d).Xow; % Equation (26)
16 PD(d).CamParams=CamParams;
17 end
References
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Shao, X.; Dai, X.; Chen, Z.; He, X. Real-time 3D digital image correlation method and its application in human pulse monitoring. Appl. Opt. 2016, 55, 696–704. [Google Scholar] [CrossRef]
- Lin, D.; Zhang, A.; Gu, J.; Chen, X.; Wang, Q.; Yang, L.; Chou, Y.; Liu, G.; Wang, J. Detection of multipoint pulse waves and dynamic 3D pulse shape of the radial artery based on binocular vision theory. Comput. Methods Programs Biomed. 2018, 155, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Tuononen, A.J. Digital Image Correlation to analyse stick-slip behaviour of tyre tread block. Tribol. Int. 2014, 69, 70–76. [Google Scholar] [CrossRef]
- Sutton, M.A.; Ke, X.; Lessner, S.M.; Goldbach, M.; Yost, M.; Zhao, F.; Schreier, H.W. Strain field measurements on mouse carotid arteries using microscopic three-dimensional digital image correlation. J. Biomed. Mater. Res. Part A 2008, 84, 178–190. [Google Scholar] [CrossRef]
- Palanca, M.; Tozzi, G.; Cristofolini, L. The use of digital image correlation in the biomechanical area: A review. Int. Biomech. 2016, 3, 1–21. [Google Scholar] [CrossRef]
- Zhang, D.; Arola, D.D. Applications of digital image correlation to biological tissues. J. Biomed. Opt. 2004, 9, 691–700. [Google Scholar] [CrossRef]
- Winkler, J.; Hendy, C. Improved structural health monitoring of London’s Docklands Light Railway bridges using Digital image correlation. Struct. Eng. Int. 2017, 27, 435–440. [Google Scholar] [CrossRef]
- Reagan, D.; Sabato, A.; Niezrecki, C. Feasibility of using digital image correlation for unmanned aerial vehicle structural health monitoring of bridges. Struct. Health Monit. 2018, 17, 1056–1072. [Google Scholar] [CrossRef]
- LeBlanc, B.; Niezrecki, C.; Avitabile, P.; Chen, J.; Sherwood, J. Damage detection and full surface characterization of a wind turbine blade using three-dimensional digital image correlation. Struct. Health Monit. 2013, 12, 430–439. [Google Scholar] [CrossRef]
- Molina-Viedma, A.J.; Felipe-Sesé, L.; López-Alba, E.; Díaz, F.A. 3D mode shapes characterisation using phase-based motion magnification in large structures using stereoscopic DIC. Mech. Syst. Signal Process. 2018, 108, 140–155. [Google Scholar] [CrossRef]
- Barone, S.; Neri, P.; Paoli, A.; Razionale, A.V. Low-frame-rate single camera system for 3D full-field high-frequency vibration measurements. Mech. Syst. Signal Process. 2019, 123, 143–152. [Google Scholar] [CrossRef]
- Bickel, V.T.; Manconi, A.; Amann, F. Quantitative assessment of digital image correlation methods to detect and monitor surface displacements of large slope instabilities. Remote Sens. 2018, 10, 865. [Google Scholar] [CrossRef] [Green Version]
- Walter, T.R.; Legrand, D.; Granados, H.D.; Reyes, G.; Arámbula, R. Volcanic eruption monitoring by thermal image correlation: Pixel offsets show episodic dome growth of the Colima volcano. J. Geophys. Res. Solid Earth 2013, 118, 1408–1419. [Google Scholar] [CrossRef] [Green Version]
- Leprince, S.; Barbot, S.; Ayoub, F.; Avouac, J.P. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1529–1558. [Google Scholar] [CrossRef] [Green Version]
- Heid, T.; Kääb, A. Evaluation of existing image matching methods for deriving glacier surface displacements globally from optical satellite imagery. Remote Sens. Environ. 2012, 118, 339–355. [Google Scholar] [CrossRef]
- Wang, P.; Pierron, F.; Thomsen, O.T. Identification of material parameters of PVC foams using digital image correlation and the virtual fields method. Exp. Mech. 2013, 53, 1001–1015. [Google Scholar] [CrossRef]
- Grédiac, M.; Pierron, F.; Surrel, Y. Novel procedure for complete in-plane composite characterization using a single T-shaped specimen. Exp. Mech. 1999, 39, 142–149. [Google Scholar] [CrossRef]
- Huchzermeyer, R. Measuring Mechanical Properties Using Digital Image Correlation: Extracting Tensile and Fracture Properties from A Single Sample. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2017. [Google Scholar]
- Leclerc, H.; Périé, J.N.; Roux, S.; Hild, F. Integrated digital image correlation for the identification of mechanical properties. In Proceedings of the International Conference on Computer Vision/Computer Graphics Collaboration Techniques and Applications, Rocquencourt, France, 4–6 May 2009; Gagalowic, A., Philips, W., Eds.; Springer: Heidelberg/Berlin, Germany, 2009; pp. 161–171. [Google Scholar]
- Chevalier, L.; Calloch, S.; Hild, F.; Marco, Y. Digital image correlation used to analyze the multiaxial behavior of rubber-like materials. Eur. J. Mech. A Solids 2001, 20, 169–187. [Google Scholar] [CrossRef] [Green Version]
- van Rooyen, M.; Becker, T.H. High-temperature tensile property measurements using digital image correlation over a non-uniform temperature field. J. Strain Anal. Eng. Des. 2018, 53, 117–129. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital imaging techniques in experimental stress analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F.; Sutton, M.A.; Chu, T.C.; Anderson, J. Application of digital correlation methods to rigid body mechanics. Opt. Eng. 1983, 22, 738–742. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Sutton, M.; Mingqi, C.; Peters, W.; Chao, Y.; McNeill, S. Application of an optimized digital correlation method to planar deformation analysis. Image Vis. Comput. 1986, 4, 143–150. [Google Scholar] [CrossRef]
- Bruck, H.A.; McNeill, S.R.; Sutton, M.A.; Peters, W.H. Digital image correlation using newton-raphson method of partial differential correction. Exp. Mech. 1989, 29, 261–267. [Google Scholar] [CrossRef]
- Luo, P.F.; Chao, Y.J.; Sutton, M.A.; Peters, W.H. Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision. Exp. Mech. 1993, 33, 123–132. [Google Scholar] [CrossRef]
- Bay, B.K.; Smith, T.S.; Fyhrie, D.P.; Saad, M. Digital volume correlation: Three-dimensional strain mapping using X-ray tomography. Exp. Mech. 1999, 39, 217–226. [Google Scholar] [CrossRef]
- Schreier, H.W.; Braasch, J.R.; Sutton, M.A. Systematic errors in digital image correlation caused by intensity interpolation. Opt. Eng. 2000, 39, 2915–2921. [Google Scholar] [CrossRef]
- Lu, H.; Cary, P.D. Deformation measurements by digital image correlation: Implementation of a second-order displacement gradient. Exp. Mech. 2000, 40, 393–400. [Google Scholar] [CrossRef]
- Baker, S.; Matthews, I. Lucas-kanade 20 years on: A unifying framework. Int. J. Comput. Vis. 2004, 56, 221–255. [Google Scholar] [CrossRef]
- Tong, W. An evaluation of digital image correlation criteria for strain mapping applications. Strain 2005, 41, 167–175. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, robust and accurate digital image correlation calculation without redundant computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Gao, Y.; Cheng, T.; Su, Y.; Xu, X.; Zhang, Y.; Zhang, Q. High-efficiency and high-accuracy digital image correlation for three-dimensional measurement. Opt. Lasers Eng. 2015, 65, 73–80. [Google Scholar] [CrossRef]
- Pan, B.; Wang, B. Digital image correlation with enhanced accuracy and efficiency: A comparison of two subpixel registration algorithms. Exp. Mech. 2016, 56, 1395–1409. [Google Scholar] [CrossRef]
- Blaber, J.; Adair, B.; Antoniou, A. Ncorr: Open-source 2D digital image correlation matlab software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Reu, P.L.; Toussaint, E.; Jones, E.; Bruck, H.A.; Iadicola, M.; Balcaen, R.; Turner, D.Z.; Siebert, T.; Lava, P.; Simonsen, M. DIC challenge: Developing images and guidelines for evaluating accuracy and resolution of 2D analyses. Exp. Mech. 2018, 58, 1067–1099. [Google Scholar] [CrossRef]
- Bloomenthal, J.; Rokne, J. Homogeneous coordinates. Vis. Comput. 1994, 11, 15–26. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Heikkila, J.; Silven, O. Four-step camera calibration procedure with implicit image correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997. [Google Scholar]
- Tsai, R.Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef] [Green Version]
- Wei, G.Q.; De Ma, S. Implicit and explicit camera calibration: Theory and experiments. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 469–480. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z. Equivalence of digital image correlation criteria for pattern matching. Appl. Opt. 2010, 49, 5501–5509. [Google Scholar] [CrossRef] [Green Version]
- Keys, R.G. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. 1981, 29, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
- Hou, H.S.; Andrews, H.C. Cubic splines for image interpolation and digital filtering. IEEE Trans. Acoust. 1978, 26, 508–517. [Google Scholar] [CrossRef]
- Pan, Z.; Chen, W.; Jiang, Z.; Tang, L.; Liu, Y.; Liu, Z. Performance of global look-up table strategy in digital image correlation with cubic B-spline interpolation and bicubic interpolation. Theor. Appl. Mech. Lett. 2016, 6, 126–130. [Google Scholar] [CrossRef] [Green Version]
- Pan, B. Bias error reduction of digital image correlation using gaussian pre-filtering. Opt. Lasers Eng. 2013, 51, 1161–1167. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z.; Qian, K.; Wang, Z. Study on subset size selection in digital image correlation for speckle patterns. Opt. Express 2008, 16, 7037–7048. [Google Scholar] [CrossRef]
- Żołądek, H. The topological proof of abel-ruffini theorem. Topol. Methods Nonlinear Anal. 2000, 16, 253–265. [Google Scholar] [CrossRef]
- Pan, B.; Asundi, A.; Xie, H.; Gao, J. Digital image correlation using iterative least squares and pointwise least squares for displacement field and strain field measurements. Opt. Lasers Eng. 2009, 47, 865–874. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, C.; Chen, J. Adaptive subset offset for systematic error reduction in incremental digital image correlation. Opt. Lasers Eng. 2014, 55, 5–11. [Google Scholar] [CrossRef]
- Foroosh, H.; Zerubia, J.B.; Berthod, M. Extension of phase correlation to subpixel registration. IEEE Trans. Image Process. 2002, 11, 188–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orteu, J.-J.; Garcia, D.; Robert, L.; Bugarin, F. A speckle texture image generator. In Proceedings of the Speckle06: Speckles, From Grains to Flowers, Nîmes, France, 13–15 September 2006; Slangen, P., Cerruti, C., Eds.; SPIE: Bellingham, WA, USA, 2006; pp. 104–109. [Google Scholar]
- Reu, P.L. Experimental and numerical methods for exact subpixel shifting. Exp. Mech. 2011, 51, 443–452. [Google Scholar] [CrossRef]
- Bornert, M.; Brémand, F.; Doumalin, P.; Dupré, J.C.; Fazzini, M.; Grédiac, M.; Hild, F.; Mistou, S.; Molimard, J.; Orteu, J.J.; et al. Assessment of digital image correlation measurement errors: Methodology and results. Exp. Mech. 2009, 49, 353–370. [Google Scholar] [CrossRef] [Green Version]
- Amiot, F.; Bornert, M.; Doumalin, P.; Dupré, J.C.; Fazzini, M.; Orteu, J.J.; Poilâne, C.; Robert, L.; Rotinat, R.; Toussaint, E.; et al. Assessment of digital image correlation measurement accuracy in the ultimate error regime: Main results of a collaborative benchmark. Strain 2013, 49, 483–496. [Google Scholar] [CrossRef] [Green Version]
- Harilal, R.; Ramji, M. Adaptation of open source 2D DIC software ncorr for solid mechanics applications. In Proceedings of the 9th International Symposium on Advanced Science and Technology in Experimental Mechanics, New Delhi, India, 1–6 November 2014. [Google Scholar]
- Lunt, D.; Thomas, R.; Roy, M.; Duff, J.; Atkinson, M.; Frankel, P.; Preuss, M.; Quinta da Fonseca, J. Comparison of sub-grain scale digital image correlation calculated using commercial and open-source software packages. Mater. Charact. 2020, 163, 110271. [Google Scholar] [CrossRef]
- Pan, B. Reliability-guided digital image correlation for image deformation measurement. Appl. Opt. 2009, 48, 1535–1542. [Google Scholar] [CrossRef] [PubMed]
- Schreier, H.W.; Sutton, M.A. Systematic errors in digital image correlation due to undermatched subset shape functions. Exp. Mech. 2002, 42, 303–310. [Google Scholar] [CrossRef]







| Variable | Variable Description |
|---|---|
| FileNames | Cell array of character vectors containing the image file names of the image set d. All images need to be the same size. |
| Mask | Logical matrix, which is the same size as the images, indicating which pixels should not be analysed during correlation. |
| GaussFilt | Define the standard deviation and window size for the Gaussian filter in pixels as [FiltSigma, FiltSize] respectively where {FiltSigma ∈ ℝ+|FiltSigma > 0} and {FiltSize ∈ ℕ}. |
| StepSize | Step size in pixels {StepSize ∈ ℕ}. |
| SubSize | Subset size in pixels {SubSize = 2k + 1|k ∈ ℕ}. |
| SubShape | Subset shape {SubShape ∈ ‘Square’, ‘Circle’}. |
| SFOrder | Dictates the SF order {SFOrder ∈ ℤ|0 ≤ SFOrder ≤ 2}. |
| RefStrat | Logical statement dictating reference image strategy (Section 3.2). |
| StopCritVal | Defines the stopping criterion value {StopCritVal ∈ ℝ+|StopCritVal > 0}. |
| WorldCTs | Location of CTs in the world CS defined according to MATLAB’s estimateCameraParameters function. |
| ImgCTs | Location of CTs in the sensor CS defined according to MATLAB’s estimateCameraParameters function. |
| rho | Calibration plate thickness in millimetres. |
| Variable | Variable Description |
|---|---|
| ImgName | Image name. |
| ImgSize(b) | Image size (b = 1 for rows and b = 2 for columns). |
| ImgFilt(b) | Standard deviation (b = 1) and window size (b = 2) for the Gaussian filter respectively in pixels. |
| SubSize(q) | Subset size in pixels. |
| SubShape(q) | Subset shape. |
| SFOrder(q) | SF order. |
| Xos(b,q) | Reference subset position in the distorted sensor CS (b = 1 for and b = 2 for ). |
| Xow(b,q) | Reference subset position in the world CS (b = 1 for and b = 2 for ). |
| P(b,q) | SFPs (b = 1 for and b = 7 for ). |
| C(q) | ZNCC coefficient. |
| Uw(b,q) | Displacement in the world CS (b = 1 for and b = 2 for ). |
| Iter(q) | Number of iterations until stopping criterion is satisfied (maximum of 100 iterations). |
| CamParams | Calibration parameters. |
| Line Numbers | Task Performed |
|---|---|
| Lines 2–4 | Compute image names, number of images and size of the first image; |
| Lines 5–6 | Create regularly spaced reference subset positions, Xos; |
| Line 7 | Remove subsets containing invalid pixels which are defined by Mask; |
| Line 8 | Pre-assign ProcData structure; |
| Line 9 | Call subroutine ImgCorr to perform image correlation; |
| Line 10 | Call subroutine CSTrans to perform transformation from the distorted sensor CS to the world CS; |
| Line Numbers | Task Performed |
|---|---|
| Line 2 | Define SubExtract function to extract square subset data; |
| Line 3 | for image number d = 2 to d = n, do |
| Line 4 | Define G |
| Line 5 | Perform Gaussian filtering on G using MATLAB’s imgaussfilt function; |
| Line 6 | Compute interpolation coefficients using MATLAB’s griddedInterpolant function; |
| Line 7 | if first image of correlation run or Refstrat is incremental, do |
| Line 8 | Define F; |
| Line 9 | Perform Gaussian filtering on F using MATLAB’s imgaussfilt function; |
| Line 10 | Compute gradients for F (compute ); |
| Lines 11–12 | Displace Xos with previous image correlation run displacements (incremental strategy); |
| Line 13 | Call subroutine PCM to compute initial estimates of displacement SFPs; |
| Line 14 | else, do |
| Line 15 | Set P(d) ← P(d − 1); |
| Line 16 | end if |
| Line 17 | Initialise temporary storage variables used to save correlation information during the inner loop; |
| Line 18 | for subset number q = 1 to number of subsets, do |
| Line 19 | Call subroutine SubShapeExtract; |
| Line 20 | Call subroutine SubCorr; |
| Line 21 | end for |
| Line 22 | Save correlation information to PD variable; |
| Line 23–24 | Show results for image d correlation; |
| Line 25 | end for |
| Line Numbers | Task Performed |
|---|---|
| Line 2 | switch SubShape; |
| Line 3 | case SubShape = ‘Square’, do |
| Line 4–6 | Extract using SubExtract; |
| Line 7 | Compute using SubSize; |
| Line 8 | case SubShape = ‘Circle’, do |
| Line 9–11 | Extract using SubExtract; |
| Line 12 | Compute using SubSize; |
| Line 13 | Determine mask of elements that fall within the circular subset; |
| Line 14–16 | Use mask to extract appropriate data for circular subset; |
| Line 17 | end switch |
| Line Numbers | Task Performed |
|---|---|
| Line 2 | Call SFExpressions to assign equations dependent on the SF order; |
| Line 3 | ; |
| Line 4 | Compute , Equation (20); |
| Line 5 | Compute normalisation values and ; |
| Line 6 | Initialise flag ← 0, iter ← 0 and ; |
| Line 7 | while flag = 0, do |
| Line 8 | Compute Equation (14), using estimates of P |
| Line 9 | Compute g using interpolation coefficients; |
| Line 10 | Compute normalisation values and ; |
| Line 11 | Compute ‖ΔP‖using Equation (23); |
| Line 12 | if ‖ΔP‖ < StopCritVal or iter > 100, do |
| Line 13 | Set iter ← 1; |
| Line 14 | Compute C, Equation (11) substituted into Equation (13); |
| Line 15 | else, do |
| Line 16 | Compute J, Summation expression of Equation (19); |
| Line 17 | Compute ΔP, Equation (19); |
| Line 18 | Update P, Equation (21); |
| Line 19 | end if |
| Line 20 | Set iter ← iter + 1 |
| Line 21 | end while |
| Line Numbers | Task Performed |
|---|---|
| Line 2 | switch SFOrder |
| Line 3–8 | case SFOrder = 0, do assign functions for zero-order SF; |
| Line 9–14 | case SFOrder = 1, do assign functions for first-order SF; |
| Line 15–20 | case SFOrder = 2, do assign functions for second-order SF; |
| Line 21 | end switch |
| Line Numbers | Task Performed |
|---|---|
| Line 2 | Compute normalised cross-power spectrum in the frequency domain; |
| Line 3 | Convert back to spatial domain; |
| Line 4 | Find index of the maximum correlation coefficient; |
| Line 5 | Compute index vector which relates indices of the correlation coefficient matrix to the displacements they correspond to; |
| Line 6–7 | Obtain displacements using index of the maximum correlation coefficient; |
| Line Numbers | Task Performed |
|---|---|
| Line 2 | if calibration targets are given, do |
| Line 3 | Compute calibration parameters using MATLAB’s estimateCameraParameters function; |
| Line 4 | else, do |
| Line 5 | Set unit calibration parameters and pass to MATLAB’s cameraParameters function; |
| Line 6 | Assign CTs in the distorted sensor and world CSs using Xos; |
| Line 7 | end if |
| Line 8 | Extract appropriate extrinsic parameters; |
| Line 9 | Compute , Equation (6); |
| Line 10 | for image number d = 1 to d = n, do |
| Lines 11–12 | Compute , Equation (24); |
| Line 13–14 | Compute and using MATLAB’s undistortPoints and pointsToWorld functions; |
| Line 15 | Compute and , Equation (26); |
| Line 16 | Save calibration parameters; |
| Line 17 | end for |
| Name | Method | Noise | Contrast | Images | Displacement field |
|---|---|---|---|---|---|
| Sample 1 | TexGen | 1.5 | Varying | 21 | Shift of 0.05 pixels in both directions per image |
| Sample 2 | TexGen | 8 | 0–50 | 21 | Shift of 0.05 pixels in both directions per image |
| Sample 3 | Fourier | 1.5 | 0–200 | 12 | Shift of 0.1 pixels in both directions per image |
| Sample 14 | Fourier | 5 | 0–200 | 4 | Sinusoid in the x-direction of increasing frequency (amplitude 0.1 pixels) |
| Code | Subset Size 21 | Subset Size 41 | Subset Size 81 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | Variance | RMSE | Bias | Variance | RMSE | Bias | Variance | RMSE | |
| ADIC2D | 2.32 | 2.59 | 3.48 | 1.08 | 0.88 | 1.4 | 0.634 | 0.481 | 0.796 |
| Ncorr | 2.31 | 2.63 | 3.5 | 0.995 | 0.822 | 1.29 | 0.504 | 0.402 | 0.645 |
| DaVis | 1.34 | 1.05 | 1.7 | 0.652 | 0.497 | 0.819 | 0.317 | 0.246 | 0.401 |
| Code | Subset Size 21 | Subset Size 41 | Subset Size 81 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | Variance | RMSE | Bias | Variance | RMSE | Bias | Variance | RMSE | |
| ADIC2D | 3.49 | 4.24 | 5.5 | 1.16 | 0.917 | 1.48 | 0.519 | 0.391 | 0.65 |
| Ncorr | 5.59 | 5.96 | 8.17 | 2.05 | 1.71 | 2.67 | 0.956 | 0.759 | 1.22 |
| DaVis | 1.84 | 1.57 | 2.42 | 0.781 | 0.599 | 0.985 | 0.377 | 0.281 | 0.47 |
| Code | Subset Size 21 | Subset Size 41 | Subset Size 81 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | Variance | RMSE | Bias | Variance | RMSE | Bias | Variance | RMSE | |
| ADIC2D | 9.75 | 8.17 | 12.7 | 3.77 | 2.9 | 4.76 | 1.87 | 1.4 | 2.34 |
| Ncorr | 9.18 | 7.58 | 11.9 | 3.97 | 3.05 | 5.01 | 2.36 | 1.7 | 2.91 |
| DaVis | 5.16 | 4.02 | 6.54 | 2.47 | 1.9 | 3.12 | 1.29 | 1 | 1.64 |
| Code/Subset Size | Displacement | Strain | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE (pix) | Variance (pix) | Max Bias (pix) | SR (pix) | RMSE (pix/pix) | Variance (pix/pix) | Max Bias (pix/pix) | SR (pix) | |
| Code G | 0.010 | 0.010 | 0.012 | 100 | 453 | 429 | 923 | 74 |
| ADIC2D 25 | 0.018 | 0.017 | 0.015 | 1629 | 598 | 406 | 1488 | 173 |
| ADIC2D 31 | 0.014 | 0.013 | 0.017 | 160 | 600 | 335 | 1674 | 182 |
| ADIC2D 51 | 0.014 | 0.007 | 0.033 | 257 | 839 | 193 | 2720 | 233 |
| ADIC2D 71 | 0.022 | 0.005 | 0.059 | 354 | 1255 | 125 | 4412 | 294 |
| Code A | 0.022 | 0.005 | 0.056 | 716 | 1131 | 172 | 3399 | 410 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atkinson, D.; Becker, T. A 117 Line 2D Digital Image Correlation Code Written in MATLAB. Remote Sens. 2020, 12, 2906. https://doi.org/10.3390/rs12182906
Atkinson D, Becker T. A 117 Line 2D Digital Image Correlation Code Written in MATLAB. Remote Sensing. 2020; 12(18):2906. https://doi.org/10.3390/rs12182906
Chicago/Turabian StyleAtkinson, Devan, and Thorsten Becker. 2020. "A 117 Line 2D Digital Image Correlation Code Written in MATLAB" Remote Sensing 12, no. 18: 2906. https://doi.org/10.3390/rs12182906
APA StyleAtkinson, D., & Becker, T. (2020). A 117 Line 2D Digital Image Correlation Code Written in MATLAB. Remote Sensing, 12(18), 2906. https://doi.org/10.3390/rs12182906