A Deep Siamese Network with Hybrid Convolutional Feature Extraction Module for Change Detection Based on Multi-sensor Remote Sensing Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Description and Training Samples Acquisition
2.1.1. Data Description
2.1.2. Training Samples Acquisition
2.2. Proposed Approach
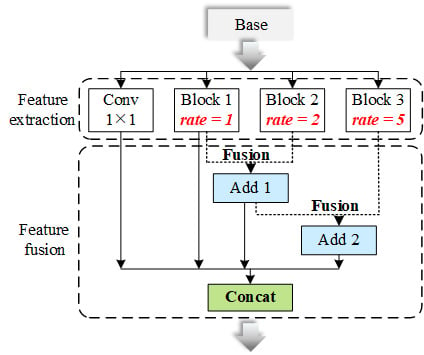
2.2.1. Hybrid Convolutional Feature Extraction Module
2.2.2. Network Architecture
2.2.3. Bootstrapping and Sampling Method for Training
2.3. Multi-Resolution Segmentation
2.4. Change Detection Framework Combined with Deep Siamese Network and Multi-Resolution Segmentation
3. Results
3.1. Experimental Results
3.2. Accuracy evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Singh, A. Digital Change Detection Techniques Using Remotely Sensed Data. Int. J. Remote Sens. 1988, 10, 989–1003. [Google Scholar] [CrossRef] [Green Version]
- Mubea, K.; Menz, G. Monitoring Land-Use Change in Nakuru (Kenya) Using Multi-Sensor Satellite Data. Adv. Remote Sens. 2012, 1, 74–84. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; He, X.; Wang, J.; Xiao, R. The Influence of Polarimetric Parameters and an Object-Based Approach on Land Cover Classification in Coastal Wetlands. Remote Sens. 2014, 6, 12575–12592. [Google Scholar] [CrossRef] [Green Version]
- Brunner, D.; Lemoine, G.; Bruzzone, L. Earthquake Damage Assessment of Buildings Using VHR Optical and SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2403–2420. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change Detection Techniques. Int. J. Remote Sens. 2004, 25, 2365–2407. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D.; Bovolo, F.; Kanevski, M.; Bruzzone, L. Supervised Change Detection in VHR Images Using Contextual Information and Support Vector Machines. Int. J. Appl. Earth Obs. Geoinf. 2013, 20, 77–85. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme Learning Machine: A New Learning Scheme of Feedforward Neural Networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Bachtiar, L.R.; Unsworth, C.P.; Newcomb, R.D.; Crampin, E.J. Multilayer Perceptron Classification of Unknown Volatile Chemicals from the Firing Rates of Insect Olfactory Sensory Neurons and Its Application to Biosensor Design. Neural Comput. 2013, 25, 259–287. [Google Scholar] [CrossRef]
- Song, X.; Cheng, B. Change Detection Using Change Vector Analysis from Landsat TM Images in Wuhan. Procedia Environ. Sci. 2011, 11, 238–244. [Google Scholar]
- Huo, C.; Zhou, Z.; Lu, H.; Pan, C.; Chen, K. Fast Object-Level Change Detection for VHR Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 118–122. [Google Scholar] [CrossRef]
- Hao, M.; Zhang, H.; Shi, W.; Deng, K. Unsupervised Change Detection Using Fuzzy C-means and MRF From Remotely Sensed Images. Remote Sens. Lett. 2013, 4, 1185–1194. [Google Scholar] [CrossRef]
- Moser, G.; Angiati, E.; Serpico, S.B. Multiscale Unsupervised Change Detection on Optical Images by Markov Random Fields and Wavelets. IEEE Geosci. Remote Sens. Lett. 2011, 8, 725–729. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, Y. Multi-Feature Object-Based Change Detection Using Self-Adaptive Weight Change Vector Analysis. Remote Sens. 2016, 8, 549. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Wen, D.; Li, J.; Qin, R. Multi-Level Monitoring of Subtle Urban Changes for The Megacities of China Using High-Resolution Multi-view Satellite Imagery. Remote Sens. Environ. 2017, 196, 56–75. [Google Scholar] [CrossRef]
- Blaschke, T. Object Based Image Analysis for Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Zhang, L.; Huang, X. Object-oriented Change Detection Based on the Kolmogorov-Smirnov Test Using High-Resolution Multispectral Imagery. Int. J. Remote Sens. 2011, 32, 5719–5740. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Zhang, Y.; Wang, L.; Ying, G. Change Detection for High-resolution Remote Sensing Imagery Using Object-Oriented Change Vector Aanalysis Method. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 2873–2876. [Google Scholar]
- Tan, K.; Zhang, Y.; Wang, X.; Chen, Y. Object-Based Change Detection Using Multiple Classifiers and Multi-Scale Uncertainty Analysis. Remote Sens. 2019, 11, 359. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zhu, X.; Wu, G.Q.; Ding, W. Data Mining With Big Data. IEEE Trans. Knowl. Data Eng. 2014, 26, 97–107. [Google Scholar] [CrossRef]
- Baltrusaitis, T.; Ahuja, C.; Morency, L.-P. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 423–443. [Google Scholar] [CrossRef] [Green Version]
- Lahat, D.; Adali, T.; Jutten, C. Multimodal Data Fusion: An Overview of Methods, Challenges, and Prospects. Proc. IEEE 2015, 103, 1449–1477. [Google Scholar] [CrossRef] [Green Version]
- Ramachandram, D.; Taylor, G.W. Deep Multimodal Learning A Survey on Recent Advances and Trends. IEEE Signal Process. Mag. 2017, 34, 96–108. [Google Scholar] [CrossRef]
- Srivastava, N.; Salakhutdinov, R. Multimodal Learning with Deep Boltzmann Machines. J. Mach. Learn. Res. 2014, 15, 2949–2980. [Google Scholar]
- Zhao, W.; Wang, Z.; Gong, M.; Liu, J. Discriminative Feature Learning for Unsupervised Change Detection in Heterogeneous Images Based on a Coupled Neural Network. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7066–7080. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change Detection Based on Deep Siamese Convolutional Network for Optical Aerial Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Mercier, G.; Moser, G.; Serpico, S.B. Conditional Copulas for Change Detection in Heterogeneous Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2014, 46, 1428–1441. [Google Scholar] [CrossRef]
- Prendes, J.; Chabert, M.; Pascal, F.; Giros, A.; Tourneret, J.-Y. A New Multivariate Statistical Model for Change Detection in Images Acquired by Homogeneous and Heterogeneous Sensors. IEEE Trans. Image Process. 2015, 24, 799–812. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Touati, R.; Mignotte, M.; Dahmane, M. A Reliable Mixed-Norm-Based Multiresolution Change Detector in Heterogeneous Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3588–3601. [Google Scholar] [CrossRef]
- Wang, X.; Tan, K.; Du, Q.; Chen, Y.; Du, P. Caps-TripleGAN: GAN-Assisted CapsNet for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7232–7245. [Google Scholar] [CrossRef]
- Tan, K.; Wu, F.; Du, Q.; Du, P.; Chen, Y. A Parallel Gaussian–Bernoulli Restricted Boltzmann Machine for Mining Area Classification With Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 627–636. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Hu, B.; Lu, Z.; Li, H.; Chen, Q. Convolutional Neural Network Architectures for Matching Natural Language Sentences. In Advances in Neural Information Processing Systems; NIPS Foundation, Inc.: San Diego, CA, USA, 2014; Volume 27. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 770–778. [Google Scholar]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully Convolutional Siamese Networks for Change Detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing, Athens, Greece, 7–10 October 2018; Volume 36, pp. 4063–4067. [Google Scholar]
- Chen, H.; Wu, C.; Du, B.; Zhang, L. Deep Siamese Multi-scale Convolutional Network for Change Detection in Multi-temporal VHR Images. arXiv 2019, arXiv:1906.11479. [Google Scholar]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A Deep Convolutional Coupling Network for Change Detection Based on Heterogeneous Optical and Radar Images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; Volume, 39, pp. 640–651. [Google Scholar]
- Holschneider, M.; Kronland-Martinet, R.; Morlet, J.; Tchamitchian, P. A Real-Time Algorithm for Signal Analysis with the Help of the Wavelet Transform. In Wavelets; Springer: Berlin/Heidelberg, Germany, 1989; pp. 286–297. [Google Scholar]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding Convolution for Semantic Segmentation. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning A Similarity Metric Discriminatively, with Application to Face Verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 539–546. [Google Scholar]
- Rahman, F.; Vasu, B.; Van Cor, J.; Kerekes, J.; Savakis, A. Siamese Network with Multi-Level Features for Patch-Based Change Detection in Satellite Imagery. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing, Anaheim, CA, USA, 26–29 November 2018; pp. 958–962. [Google Scholar]
- Hay, G.J.; Blaschke, T.; Marceau, D.J.; Bouchard, A. A Comparison of Three Image-Object Methods for The Multiscale Analysis of Landscape Structure. ISPRS J. Photogramm. Remote Sens. 2003, 57, 327–345. [Google Scholar] [CrossRef]
- Zhang, X.; Du, S. Learning Selfhood Scales for Urban Land Cover Mapping with Very-High-Resolution Satellite Images. Remote Sens. Environ. 2016, 178, 172–190. [Google Scholar] [CrossRef]
- Lu, Q.; Ma, Y.; Xia, G.-S. Active Learning for Training Sample Selection in Remote Sensing Image Classification Using Spatial Information. Remote Sens. Lett. 2017, 8, 1211–1220. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter Selection for Region-Growing Image Segmentation Algorithms Using Spatial Autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]












| Satellite | Payload | Band | Spectrum Range (μm) | Spatial Resolution (m) | Time |
|---|---|---|---|---|---|
| ZY-3 | MUX | Blue | 0.45~0.52 | 5.8 | 2014.10.14 |
| Green | 0.52~0.59 | ||||
| Red | 0.63~0.69 | ||||
| Nir | 0.77~0.89 | ||||
| GF-2 | PMS | Blue | 0.45~0.52 | 4 | 2016.10.05 |
| Green | 0.52~0.59 | ||||
| Red | 0.63~0.69 | ||||
| Nir | 0.77~0.89 |
| Method | OA | Kappa | Commission | Omission |
|---|---|---|---|---|
| MLR | 0.9413 | 0.5802 | 0.4242 | 0.3474 |
| ELM | 0.9447 | 0.6033 | 0.4022 | 0.3270 |
| SVM | 0.9470 | 0.6097 | 0.3817 | 0.3405 |
| ANN | 0.9378 | 0.5850 | 0.4528 | 0.2895 |
| DCNN | 0.9268 | 0.5805 | 0.5094 | 0.1655 |
| TSCNN | 0.9382 | 0.5544 | 0.4421 | 0.3791 |
| DSMS-CN | 0.9391 | 0.6459 | 0.4573 | 0.0998 |
| OB-DSCNH (ω = 7, l = 40) | 0.9715 | 0.7801 | 0.1894 | 0.2193 |
| Method | OA | Kappa | Commission | Omission |
|---|---|---|---|---|
| MLR | 0.8682 | 0.3032 | 0.5971 | 0.6466 |
| ELM | 0.8630 | 0.3232 | 0.6051 | 0.5937 |
| SVM | 0.8803 | 0.3167 | 0.5440 | 0.6729 |
| ANN | 0.8416 | 0.3085 | 0.6523 | 0.5362 |
| DCNN | 0.8783 | 0.5074 | 0.5263 | 0.2697 |
| TSCNN | 0.8820 | 0.4223 | 0.5229 | 0.4986 |
| DSMS-CN | 0.9247 | 0.6799 | 0.3822 | 0.1313 |
| OB-DSCNH (ω = 13, l = 30) | 0.9468 | 0.7351 | 0.2392 | 0.2305 |
| Method | OA | Kappa | Commission | Omission |
|---|---|---|---|---|
| MLR | 0.9548 | 0.4818 | 0.5335 | 0.4488 |
| ELM | 0.9442 | 0.4783 | 0.5979 | 0.3184 |
| SVM | 0.9581 | 0.4932 | 0.5006 | 0.4683 |
| ANN | 0.9145 | 0.3886 | 0.7041 | 0.2434 |
| DCNN | 0.9491 | 0.5692 | 0.5542 | 0.1139 |
| TSCNN | 0.9539 | 0.5107 | 0.5374 | 0.3676 |
| DSMS-CN | 0.9502 | 0.5889 | 0.5457 | 0.0621 |
| OB-DSCNH (ω = 9, l = 45) | 0.9792 | 0.7549 | 0.2756 | 0.1879 |
| ω | OA | Kappa | Commission | Omission |
|---|---|---|---|---|
| 5 | 0.9475 | 0.6256 | 0.3862 | 0.3003 |
| 7 | 0.9445 | 0.6619 | 0.4293 | 0.1247 |
| 9 | 0.9335 | 0.6124 | 0.4810 | 0.1425 |
| 11 | 0.9295 | 0.6033 | 0.4982 | 0.1202 |
| 13 | 0.9394 | 0.6406 | 0.4548 | 0.1241 |
| ω | OA | Kappa | Commission | Omission |
|---|---|---|---|---|
| 7 | 0.8929 | 0.5769 | 0.4849 | 0.1701 |
| 9 | 0.9138 | 0.6437 | 0.4208 | 0.1420 |
| 11 | 0.9167 | 0.6545 | 0.4114 | 0.1340 |
| 13 | 0.9244 | 0.6759 | 0.3810 | 0.1446 |
| 15 | 0.9236 | 0.6720 | 0.3832 | 0.1503 |
| ω | OA | Kappa | Commission | Omission |
|---|---|---|---|---|
| 5 | 0.9537 | 0.5830 | 0.5292 | 0.1521 |
| 7 | 0.9498 | 0.5791 | 0.5495 | 0.0900 |
| 9 | 0.9619 | 0.6476 | 0.4740 | 0.0915 |
| 11 | 0.9524 | 0.5928 | 0.5352 | 0.0899 |
| 13 | 0.9543 | 0.6016 | 0.5243 | 0.0955 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Tan, K.; Jia, X.; Wang, X.; Chen, Y. A Deep Siamese Network with Hybrid Convolutional Feature Extraction Module for Change Detection Based on Multi-sensor Remote Sensing Images. Remote Sens. 2020, 12, 205. https://doi.org/10.3390/rs12020205
Wang M, Tan K, Jia X, Wang X, Chen Y. A Deep Siamese Network with Hybrid Convolutional Feature Extraction Module for Change Detection Based on Multi-sensor Remote Sensing Images. Remote Sensing. 2020; 12(2):205. https://doi.org/10.3390/rs12020205
Chicago/Turabian StyleWang, Moyang, Kun Tan, Xiuping Jia, Xue Wang, and Yu Chen. 2020. "A Deep Siamese Network with Hybrid Convolutional Feature Extraction Module for Change Detection Based on Multi-sensor Remote Sensing Images" Remote Sensing 12, no. 2: 205. https://doi.org/10.3390/rs12020205
APA StyleWang, M., Tan, K., Jia, X., Wang, X., & Chen, Y. (2020). A Deep Siamese Network with Hybrid Convolutional Feature Extraction Module for Change Detection Based on Multi-sensor Remote Sensing Images. Remote Sensing, 12(2), 205. https://doi.org/10.3390/rs12020205