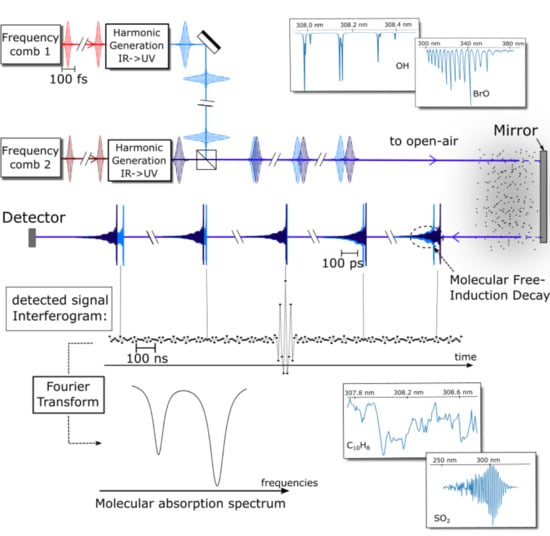
Towards DCS in the UV Spectral Range for Remote Sensing of Atmospheric Trace Gases
Abstract
:| Contents | ||
| 1 | Introduction | 2 |
| 2 | Dual-Comb Spectroscopy | 3 |
| 2.1 Principle............................................................................................................................................................................ | 3 | |
| 2.2 UV-DCS Spectrometer Signal Fluctuations.................................................................................................................... | 5 | |
| 3 | UV-DCS Laser Sources | 6 |
| 4 | UV Light Propagation into the Atmosphere | 8 |
| 4.1 Atmosphere-Induced Amplitude Noise.......................................................................................................................... | 8 | |
| 4.2 Atmosphere-Induced Phase Noise................................................................................................................................... | 8 | |
| 5 | Results: Simulated UV-DCS Sensitivity | 9 |
| 5.1 Quality Factor and Minimum Absorption Sensitivity................................................................................................... | 9 | |
| 5.2 Case (1): 308 nm: Narrow Spectral Range and High Spectral Resolution.................................................................. | 10 | |
| 5.3 Case (2): 350 nm: Broad Spectral Range and Low Spectral Resolution....................................................................... | 11 | |
| 5.4 Results on Concentration Detection Limits.................................................................................................................... | 11 | |
| 6 | Discussion | 12 |
| 7 | Conclusions | 13 |
| A Multiplicative Noise Due to Residual Relative Optical Phase Noise | 14 | |
| References | 15 | |
1. Introduction
2. Dual-Comb Spectroscopy
2.1. Principle
2.2. UV-DCS Spectrometer Signal Fluctuations
3. UV-DCS Laser Sources
4. UV Light Propagation into the Atmosphere
4.1. Atmosphere-Induced Amplitude Noise
4.2. Atmosphere-Induced Phase Noise
5. Results: Simulated UV-DCS Sensitivity
5.1. Quality Factor and Minimum Absorption Sensitivity
5.2. Case (1): 308 nm: Narrow Spectral Range and High Spectral Resolution
5.3. Case (2): 350 nm: Broad Spectral Range and Low Spectral Resolution
5.4. Results on Concentration Detection Limits
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DCS | Dual-Comb Spectroscopy |
| OFC | Optical Frequency Comb |
| SNR | Signal/Noise Ratio |
| PSD | Power Spectral Density |
| RIN | Relative Intensity Noise |
| NEP | Noise Equivalent Power |
| IGM | Interferogram |
| MAS | Minimum Absorption Sensitivity |
| DOAS | Differential Optical Absorption Spectroscopy |
| MOAS | Multipass Optical Absorption Spectroscopy |
Appendix A. Multiplicative Noise Due to Residual Relative Optical Phase Noise
| Case Study | Components | |||
|---|---|---|---|---|
| Case (1) | ||||
| OH | 1 / 111 | 8.9 | 1 | |
| Naphthalene | 1/ 33 | 3 | 2 | |
| Formaldehyde | 1/ 33 | 3 | 2 | |
| SO2 | 1/ 22 | 5 | 2 | |
| Case (2) | ||||
| BrO/Formaldehyde | 1/25 | 9.3 | 3 |
References
- Wei, Y.; Wang, Y.; Wu, X.; Di, Q.; Shi, L.; Koutrakis, P.; Zanobetti, A.; Dominici, F.; Schwartz, J.D. Causal Effects of Air Pollution on Mortality in Massachusetts. Am. J. Epidemiol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Hodgkinson, J.; Tatam, R.P. Optical gas sensing: A review. Meas. Sci. Technol. 2012, 24, 012004. [Google Scholar] [CrossRef] [Green Version]
- Shutler, J.D.; Quartly, G.D.; Donlon, C.J.; Sathyendranath, S.; Platt, T.; Chapron, B.; Johannessen, J.A.; Girard-Ardhuin, F.; Nightingale, P.D.; Woolf, D.K.; et al. Progress in satellite remote sensing for studying physical processes at the ocean surface and its borders with the atmosphere and sea ice. Prog. Phys. Geogr. Earth Environ. 2016, 40, 215–246. [Google Scholar] [CrossRef] [Green Version]
- Heymann, J.; Reuter, M.; Buchwitz, M.; Schneising, O.; Bovensmann, H.; Burrows, J.P.; Massart, S.; Kaiser, J.W.; Crisp, D. CO2 emission of Indonesian fires in 2015 estimated from satellite-derived atmospheric CO2 concentrations. Geophys. Res. Lett. 2017, 44, 1537–1544. [Google Scholar] [CrossRef]
- Bousquet, P.; Pierangelo, C.; Bacour, C.; Marshall, J.; Peylin, P.; Ayar, P.V.; Ehret, G.; Bréon, F.M.; Chevallier, F.; Crevoisier, C.; et al. Error Budget of the MEthane Remote LIdar missioN and Its Impact on the Uncertainties of the Global Methane Budget. J. Geophys. Res. Atmos. 2018, 123, 11,766–11,785. [Google Scholar] [CrossRef]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy: Principles and Applications; Springer: Berlin/Heidelberg, Germnay, 2008. [Google Scholar] [CrossRef] [Green Version]
- Davis, S.P.; Abrams, M.C.; Brault, J.W. Fourier Transform Spectrometry; Academic Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
- O’Keefe, A.; Deacon, D.A.G. Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources. Rev. Sci. Instrum. 1988, 59, 2544–2551. [Google Scholar] [CrossRef] [Green Version]
- Courtillot, I.; Morville, J.; Motto-Ros, V. Sub-ppb NO2 detection by optical feedback cavity-enhanced absorption spectroscopy with a blue diode laser. Appl. Phys. B 2006, 85, 407. [Google Scholar] [CrossRef]
- Crosson, E. A cavity ring-down analyzer for measuring atmospheric levels of methane, carbon dioxide, and water vapor. Appl. Phys. B 2008, 92, 403. [Google Scholar] [CrossRef]
- Megie, G. Laser Remote Sensing: Fundamentals and Applications. Eos, Trans. Am. Geophys. Union 1985, 66, 686. [Google Scholar] [CrossRef]
- Rossi, R.; Di Giovanni, D.; Malizia, A.; Gaudio, P. Measurements of Vehicle Pollutants in a High-Traffic Urban Area by a Multiwavelength Dial Approach: Correlation Between Two Different Motor Vehicle Pollutants. Atmosphere 2020, 11, 383. [Google Scholar] [CrossRef] [Green Version]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of Absorption and Optical Properties of Key Aerosol Types Observed in Worldwide Locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- David, G.; Miffre, A.; Thomas, B.; Rairoux, P. Sensitive and accurate dual-wavelength UV-VIS polarization detector for optical remote sensing of tropospheric aerosols. Appl. Phys. B 2012, 108, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Kolehmainen, M.; Martikainen, H.; Ruuskanen, J. Neural networks and periodic components used in air quality forecasting. Atmos. Environ. 2001, 35, 815–825. [Google Scholar] [CrossRef]
- Postolache, O.A.; Dias Pereira, J.M.; Silva Girao, P.M.B. Smart Sensors Network for Air Quality Monitoring Applications. IEEE Trans. Instrum. Meas. 2009, 58, 3253–3262. [Google Scholar] [CrossRef]
- Carnevale, C.; Finzi, G.; Pisoni, E.; Volta, M. Neuro-fuzzy and neural network systems for air quality control. Atmos. Environ. 2009, 43, 4811–4821. [Google Scholar] [CrossRef]
- Méjean, G.; Kassi, S.; Romanini, D. Measurement of reactive atmospheric species by ultraviolet cavity-enhanced spectroscopy with a mode-locked femtosecond laser. Opt. Lett. 2008, 33, 1231–1233. [Google Scholar] [CrossRef]
- Gherman, T.; Venables, D.S.; Vaughan, S.; Orphal, J.; Ruth, A.A. Incoherent Broadband Cavity-Enhanced Absorption Spectroscopy in the near-Ultraviolet: Application to HONO and NO2. Environ. Sci. Technol. 2008, 42, 890–895. [Google Scholar] [CrossRef]
- Amediek, A.; Ehret, G.; Fix, A.; Wirth, M.; Büdenbender, C.; Quatrevalet, M.; Kiemle, C.; Gerbig, C. CHARM-F—A new airborne integrated-path differential-absorption lidar for carbon dioxide and methane observations: Measurement performance and quantification of strong point source emissions. Appl. Opt. 2017, 56, 5182–5197. [Google Scholar] [CrossRef]
- Wagner, G.A.; Plusquellic, D.F. Ground-based, integrated path differential absorption LIDAR measurement of CO2, CH4, and H2O near 1.6 mu. Appl. Opt. 2016, 55, 6292–6310. [Google Scholar] [CrossRef]
- Rairoux, P.; Schillinger, H.; Niedermeier, S.; Rodriguez, M.; Ronneberger, F.; Sauerbrey, R.; Stein, B.; Waite, D.; Wedekind, C.; Wille, H.; et al. Remote sensing of the atmosphere using ultrashort laser pulses. Appl. Phys. B 2000, 71, 573–580. [Google Scholar] [CrossRef]
- Kasparian, J.; Rodriguez, M.; Méjean, G.; Yu, J.; Salmon, E.; Wille, H.; Bourayou, R.; Frey, S.; Andre, Y.B.; Mysyrowicz, A.; et al. White-light filaments for atmospheric analysis. Science 2003, 301, 61–64. [Google Scholar] [CrossRef] [PubMed]
- Rieker, G.B.; Giorgetta, F.R.; Swann, W.C.; Kofler, J.; Zolot, A.M.; Sinclair, L.C.; Baumann, E.; Cromer, C.; Petron, G.; Sweeney, C.; et al. Frequency-comb-based remote sensing of greenhouse gases over kilometer air paths. Optica 2014, 1, 290–298. [Google Scholar] [CrossRef]
- Schroeder, P.; Wright, R.; Coburn, S.; Sodergren, B.; Cossel, K.; Droste, S.; Truong, G.; Baumann, E.; Giorgetta, F.; Coddington, I.; et al. Dual frequency comb laser absorption spectroscopy in a 16 MW gas turbine exhaust. Proc. Combust. Inst. 2017, 36, 4565–4573. [Google Scholar] [CrossRef] [Green Version]
- Oudin, J.; Mohamed, A.K.; Hébert, P.J. IPDA LIDAR measurements on atmospheric CO2 and H2O using dual comb spectroscopy. Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. In Proceedings of the International Conference on Space Optics-ICSO 2018, Chania, Greece, 9–12 October 2018; Volume 11180, p. 111802N. [Google Scholar] [CrossRef] [Green Version]
- Millot, G.; Pitois, S.; Yan, M.; Hovhannisyan, T.; Bendahmane, A.; Hänsch, T.W.; Picqué, N. Frequency-agile dual-comb spectroscopy. Nat. Photonics 2016, 10, 27–30. [Google Scholar] [CrossRef]
- Schubert, O.; Eisele, M.; Crozatier, V.; Forget, N.; Kaplan, D.; Huber, R. Rapid-scan acousto-optical delay line with 34 kHz scan rate and 15 as precision. Opt. Lett. 2013, 38, 1910–2907. [Google Scholar] [CrossRef] [Green Version]
- Baumann, E.; Giorgetta, F.R.; Swann, W.C.; Zolot, A.M.; Coddington, I.; Newbury, N.R. Spectroscopy of the methane ν3 band with an accurate midinfrared coherent dual-comb spectrometer. Phys. Rev. A 2011, 84, 062513. [Google Scholar] [CrossRef] [Green Version]
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef] [Green Version]
- Picqué, N.; Hänsch, T.W. Frequency comb spectroscopy. Nat. Photonics 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Meek, S.A.; Hipke, A.; Guelachvili, G.; Hänsch, T.W.; Picqué, N. Doppler-free Fourier transform spectroscopy. Opt. Lett. 2018, 43, 162–165. [Google Scholar] [CrossRef] [Green Version]
- Keilmann, F.; Gohle, C.; Holzwarth, R. Time-domain mid-infrared frequency-comb spectrometer. Opt. Lett. 2004, 29, 1542–1544. [Google Scholar] [CrossRef] [Green Version]
- Schliesser, A.; Brehm, M.; Keilmann, F.; Weide, D.W.V.D. Frequency-comb infrared spectrometer for rapid, remote chemical sensing. Opt. Express 2005, 13, 9029–9038. [Google Scholar] [CrossRef] [PubMed]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical frequency metrology. Nature 2002, 415, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279–1295. [Google Scholar] [CrossRef] [Green Version]
- Hänsch, T.W. Nobel Lecture: Passion for precision. Rev. Mod. Phys. 2006, 78, 1297–1309. [Google Scholar] [CrossRef] [Green Version]
- Newbury, N.R.; Coddington, I.; Swann, W. Sensitivity of coherent dual-comb spectroscopy. Opt. Express 2010, 18, 7929–7945. [Google Scholar] [CrossRef]
- Peters, E.; Diddams, S.A.; Fendel, P.; Reinhardt, S.; Hänsch, T.W.; Udem, T. A deep-UV optical frequency comb at 205 nm. Opt. Express 2009, 17, 9183–9190. [Google Scholar] [CrossRef]
- Benko, C.; Allison, T.K.; Cingöz, A.; Hua, L.; Labaye, F.; Yost, D.C.; Ye, J. Extreme ultraviolet radiation with coherence time greater than 1 s. Nat. Photonics 2014, 8, 530–536. [Google Scholar] [CrossRef] [Green Version]
- Liehl, A.; Sulzer, P.; Fehrenbacher, D.; Rybka, T.; Seletskiy, D.V.; Leitenstorfer, A. Deterministic Nonlinear Transformations of Phase Noise in Quantum-Limited Frequency Combs. Phys. Rev. Lett. 2019, 122, 203902. [Google Scholar] [CrossRef] [Green Version]
- Ideguchi, T.; Poisson, A.; Guelachvili, G.; Hänsch, T.W.; Picqué, N. Adaptive dual-comb spectroscopy in the green region. Opt. Lett. 2012, 37, 4847–4849. [Google Scholar] [CrossRef] [Green Version]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent Multiheterodyne Spectroscopy Using Stabilized Optical Frequency Combs. Phys. Rev. Lett. 2008, 100, 013902. [Google Scholar] [CrossRef] [Green Version]
- Ideguchi, T.; Poisson, A.; Guelachvili, G.; Picqué, N.; Hänsch, T.W. Adaptive real-time dual-comb spectroscopy. Nat. Commun. 2014, 5, 3375. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Fonseca-Campos, J.; Liang, W.G.; Xu, C.Q.; Vargas-Baca, I. Noise Analysis of Second-Harmonic Generation in Undoped and MgO-Doped Periodically Poled Lithium Niobate. Adv. OptoElectron. 2008, 2008. [Google Scholar] [CrossRef] [Green Version]
- Tawfieq, M.; Hansen, A.K.; Jensen, O.B.; Marti, D.; Sumpf, B.; Andersen, P.E. Intensity Noise Transfer Through a Diode-Pumped Titanium Sapphire Laser System. IEEE J. Quantum. Electron. 2018, 54, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent linear optical sampling at 15 bits of resolution. Opt. Lett. 2009, 34, 2153. [Google Scholar] [CrossRef] [PubMed]
- Moutzouris, K.; Sotier, F.; Adler, F.; Leitenstorfer, A. Highly efficient second, third and fourth harmonic generation from a two-branch femtosecond erbium fiber source. Opt. Express 2006, 14, 1905–1912. [Google Scholar] [CrossRef]
- Kuzucu, O.; Wong, F.N.C.; Zelmon, D.E.; Hegde, S.M.; Roberts, T.D.; Battle, P. Generation of 250 mW narrowband pulsed ultraviolet light by frequency quadrupling of an amplified erbium-doped fiber laser. Opt. Lett. 2007, 32, 1290–1292. [Google Scholar] [CrossRef] [PubMed]
- Carlson, D.R. Frequency Combs for Spectroscopy in the Vacuum Ultraviolet. Ph.D. Thesis, University of Arizona, Tucson, Arizona, 2016. [Google Scholar]
- Schuster, V.; Liu, C.; Klas, R.; Dominguez, P.; Rothhardt, J.; Limpert, J.; Bernhardt, B. Towards Dual Comb Spectroscopy in the Ultraviolet Spectral Region. Available online: https://arxiv.org/abs/2006.03309 (accessed on 5 June 2020).
- Rotermund, F.; Petrov, V. Generation of the fourth harmonic of a femtosecond Ti:sapphire laser. Opt. Lett. 1998, 23, 1040–1042. [Google Scholar] [CrossRef] [PubMed]
- Petrov, V.; Ghotbi, M.; Kokabee, O.; Esteban-Martin, A.; Noack, F.; Gaydardzhiev, A.; Nikolov, I.; Tzankov, P.; Buchvarov, I.; Miyata, K.; et al. Femtosecond nonlinear frequency conversion based on BiB3O6. Laser Photonics Rev. 2010, 4, 53–98. [Google Scholar] [CrossRef]
- Kanseri, B.; Bouillard, M.; Tualle-Brouri, R. Efficient frequency doubling of femtosecond pulses with BIBO in an external synchronized cavity. Opt. Commun. 2016, 380, 148–153. [Google Scholar] [CrossRef]
- Sutyrin, D.V.; Poli, N.; Beverini, N.; Tino, G.M. Carrier-envelope offset frequency noise analysis in Ti:sapphire frequency combs. Opt. Eng. 2014, 12, 122603. [Google Scholar] [CrossRef]
- Quraishi, Q.; Diddams, S.A.; Hollberg, L. Optical phase-noise dynamics of Titanium:sapphire optical frequency combs. Opt. Commun. 2014, 320, 84–87. [Google Scholar] [CrossRef] [Green Version]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent dual-comb spectroscopy at high signal-to-noise ratio. Phys. Rev. A 2010, 82, 043817. [Google Scholar] [CrossRef] [Green Version]
- Mulder, T.D.; Scott, R.P.; Kolner, B.H. Amplitude and envelope phase noise of a modelocked laser predicted from its noise transfer function and the pump noise power spectrum. Opt. Express 2008, 16, 14186–14191. [Google Scholar] [CrossRef] [PubMed]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: Cambridge, UK, 1978. [Google Scholar] [CrossRef]
- Armerding, W.; Spiekermann, M.; Walter, J.; Comes, F.J. Multipass optical absorption spectroscopy: A fast-scanning laser spectrometer for the in situ determination of atmospheric trace-gas components, in particular OH. Appl. Opt. 2008, 35, 4206. [Google Scholar] [CrossRef] [PubMed]
- Backus, S.; Asaki, M.T.; Shi, C.; Kapteyn, H.C.; Murnane, M.M. Intracavity frequency doubling in a Ti:sapphire laser: Generation of 14-fs pulses at 416 nm. Opt. Lett. 1994, 19, 399–401. [Google Scholar] [CrossRef] [PubMed]
- Steinbach, D.; Hügel, W.; Wegener, M. Generation and detection of blue 10.0-fs pulses. J. Opt. Soc. Am. B 1998, 15, 1231–1234. [Google Scholar] [CrossRef]
- Fürbach, A.; Le, T.; Spielmann, C.; Krausz, F. Generation of 8-fs pulses at 390 nm. Appl. Phys. B 2000, 70, 37–40. [Google Scholar] [CrossRef]
- Fuchs, H.; Dorn, H.P.; Bachner, M.; Bohn, B.; Brauers, T.; Gomm, S.; Hofzumahaus, A.; Holland, F.; Nehr, S.; Rohrer, F.; et al. Comparison of OH concentration measurements by DOAS and LIF during SAPHIR chamber experiments at high OH reactivity and low NO concentration. Atmos. Meas. Tech. 2012, 5, 1611–1626. [Google Scholar] [CrossRef] [Green Version]
- Stutz, J.; Oh, H.J.; Whitlow, S.I.; Anderson, C.; Dibb, J.E.; Flynn, J.H.; Rappenglack, B.; Lefer, B. Simultaneous DOAS and mist-chamber IC measurements of HONO in Houston, TX. Atmos. Environ. 2010, 44, 4090–4098. [Google Scholar] [CrossRef]
- Hausmann, M.; Brandenburger, U.; Brauers, T.; Dorn, H.P. Detection of tropospheric OH radicals by long-path differential-optical-absorption spectroscopy: Experimental setup, accuracy, and precision. J. Geophys. Res. Atmos. 1997, 102, 16011–16022. [Google Scholar] [CrossRef]
- Vandaele, A.C.; Carleer, M. Development of Fourier transform spectrometry for UV-visible differential optical absorption spectroscopy measurements of tropospheric minor constituents. Appl. Opt. 1999, 38, 2630. [Google Scholar] [CrossRef] [PubMed]
- Hebestreit, K.; Stutz, J.; Rosen, D.; Matveiv, V.; Peleg, M.; Luria, M.; Platt, U. DOAS Measurements of Tropospheric Bromine Oxide in Mid-Latitudes. Science 1999, 283, 55–57. [Google Scholar] [CrossRef]
- Hönninger, G.; Leser, H.; Sebastián, O.; Platt, U. Ground-based measurements of halogen oxides at the Hudson Bay by active longpath DOAS and passive MAX-DOAS. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]




| Quantity | Variable | Value |
|---|---|---|
| Repetition frequency | 100 [Hz] | |
| Relative Intensity Noise | RIN | −125 [dBc/Hz] a or −129 [dBc/Hz] b |
| Noise Equivalent power | NEP | 0.44 [W/] c |
| Detection dynamic range | D | 12 bits |
| Experimental geometry | 0.5 d |
| Case-Study | Quality Factor Q | () | Minimum Absorption Sensitivity: MAS |
|---|---|---|---|
| (; M; ) | |||
| Case (1) | 1.0 | (100 MHz; 200 Hz) | 2.1 |
| (2.5 GHz; 1200; 25 ) | * (OH: 1.0 ) | ||
| Case (2) | 1.6 | (200 MHz; 200 Hz) | 3.1 |
| (5 GHz; 10,000; 25 ) |
| Component | Study Case | Differential Cross-Section | Concentration |
|---|---|---|---|
| [cm2/molec.] | Detection Limit [ppt] | ||
| SO2 | Case (1) | 1.2 | 260 |
| Case (2) | 5.7 | 700 | |
| CH2O (formaldehyde) | Case (1) | 1.5 | 210 |
| Case (2) | 0.48 | 625 | |
| C8H10 (naphthalene) | Case (1) | 15 | 20 |
| OH | Case (1) | 1670 | 0.08 |
| BrO | Case (2) | 104 | 38 |
| OClO | Case (2) | 107 | 38 |
| HONO | Case (2) | 4 | 1000 |
| NO2 | Case (2) | 2.5 | 1600 |
| Experiment Type | MAS at 1 s | |
|---|---|---|
| Case (1) | ||
| LP-DOAS [64,65,66] | [2–3] | |
| MOAS [60] | [1–2] | |
| UV-FTS [67] | [1–2] | |
| UV-DCS (numerical study, this work) | [1–6] | |
| Case (2) | ||
| LP-DOAS [65,68,69] | 2 | |
| UV-FTS [67] | 0.2 | |
| UV-DCS (numerical study, this work) | [1–3] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galtier, S.; Pivard, C.; Rairoux, P. Towards DCS in the UV Spectral Range for Remote Sensing of Atmospheric Trace Gases. Remote Sens. 2020, 12, 3444. https://doi.org/10.3390/rs12203444
Galtier S, Pivard C, Rairoux P. Towards DCS in the UV Spectral Range for Remote Sensing of Atmospheric Trace Gases. Remote Sensing. 2020; 12(20):3444. https://doi.org/10.3390/rs12203444
Chicago/Turabian StyleGaltier, Sandrine, Clément Pivard, and Patrick Rairoux. 2020. "Towards DCS in the UV Spectral Range for Remote Sensing of Atmospheric Trace Gases" Remote Sensing 12, no. 20: 3444. https://doi.org/10.3390/rs12203444
APA StyleGaltier, S., Pivard, C., & Rairoux, P. (2020). Towards DCS in the UV Spectral Range for Remote Sensing of Atmospheric Trace Gases. Remote Sensing, 12(20), 3444. https://doi.org/10.3390/rs12203444