An Efficient Spectral Feature Extraction Framework for Hyperspectral Images
Abstract
:1. Introduction
- (1)
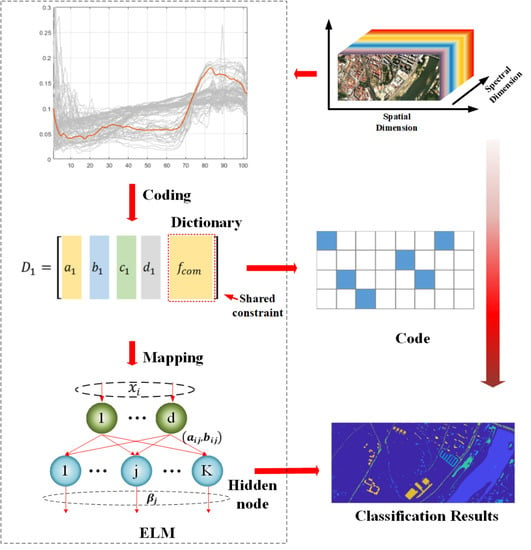
- We design an efficient feature learning framework that calculates the structured dictionary to encode spectral information and adopts machine learning to map the coding coefficients. The block-diagonal constraint is applied to increase the efficiency of coding, and an effective extreme learning machine (ELM) is employed to complete the mapping.
- (2)
- We apply spectral convolution to extract the mean value and local variation of the spectra of HSIs. Then, the dictionary learning is carried out to capture more local spectral characteristics of HSI data.
- (3)
- We devise a new shared constraint for all of the subdictionaries. In this way, the common and specific features of HSI samples will be learned separately to achieve a more discriminative representation.
2. Materials and Methods
2.1. The Study Datasets
2.2. Related Works
2.2.1. Review of Sparse Representation-Based Classification
2.2.2. Review of Class-Specific Dictionary Learning
2.2.3. Review of Fisher Discriminant Dictionary Learning
2.3. Proposed Framework
2.3.1. Spectral Convolution
2.3.2. Structured Dictionary
2.3.3. Shared Constraint
2.3.4. Feature Extraction Framework
3. Experimental Results and Discussion
3.1. Compared Methods and Evaluation Indexes
3.2. Discussions of Different Datasets
3.3. Small Training Samples
3.4. Time Cost
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dou, P.; Zeng, C. Hyperspectral Image Classification Using Feature Relations Map Learning. Remote Sens. 2020, 12, 2956. [Google Scholar] [CrossRef]
- Santos-Rufo, A.; Mesas-Carrascosa, F.-J.; García-Ferrer, A.; Meroño-Larriva, J.E. Wavelength Selection Method Based on Partial Least Square from Hyperspectral Unmanned Aerial Vehicle Orthomosaic of Irrigated Olive Orchards. Remote Sens. 2020, 12, 3426. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Gamba, P.; Bioucas-Dias, J.M.; Zhang, L.; Benediktsson, J.A.; Plaza, A. Multiple Feature Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1592–1606. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Shi, Z. Hyperspectral Image Target Detection Improvement Based on Total Variation. IEEE Trans. Image Process. 2016, 25, 2249–2258. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Deng, C.; Chanussot, J.; Hong, D.; Zhao, B. Stfnet: A two-stream convolutional neural network for spatiotemporal image fusion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6552–6564. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Bayliss, J.; Gualtieri, J.; Cromp, R. Analysing hyperspectral data with independent component analysis. Proc. Int. Soc. Opt. Eng. 1997, 3240, 133–143. [Google Scholar]
- Rodarmel, C.; Shan, J. Principal Component Analysis for Hyperspectral Image Classification. Surv. Land Inf. Syst. 2002, 62, 115–122. [Google Scholar]
- Ji, S.; Ye, J. Generalized linear discriminant analysis: A unified framework and efficient model selection. IEEE Trans. Neural Netw. 2008, 19, 1768–1782. [Google Scholar]
- Scholkopf, B.; Smola, A. Learning with Kernels? Support Vector Machines, Regularization, Optimization and Beyond; MIT Press: Cambridge, MA, USA, 2002; pp. 1768–1782. [Google Scholar]
- Camps-Valls, G.; Bruzzone, L. Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef]
- Archibald, R.; Fann, G. Feature selection and classification of hyperspectral images with support vector machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Bahria, S.; Essoussi, N.; Limam, M. Hyperspectral data classification using geostatistics and support vector machines. Remote Sens. Lett. 2011, 2, 99–106. [Google Scholar] [CrossRef]
- Bruzzone, L.; Chi, M.; Marconcini, M. A novel transductive svm for semisupervised classification of remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3363–3373. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectralcspatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Du, S. Spectral-spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature Extraction for Hyperspectral Imagery: The Evolution from Shallow to Deep (Overview and Toolbox). arXiv 2020, arXiv:2003.02822. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.; Ganesh, A.; Sastry, S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Nasrabadi, N.; Tran, T. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.; Tran, T. Hyperspectral image classification via kernel sparse representation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 217–231. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Tsang, I.; Chia, L. Sparse representation with kernels. IEEE Trans. Image Process. 2013, 22, 423–434. [Google Scholar]
- Li, C.; Ma, Y.; Mei, X.; Liu, C.; Ma, J. Hyperspectral image classification with robust sparse representation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 641–645. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, B. Discriminative k-svd for dictionary learning in face recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2691–2698. [Google Scholar]
- Du, P.; Xue, Z.; Li, J.; Plaza, A. Learning discriminative sparse representations for hyperspectral image classification. IEEE J. Sel. Top. Signal Process. 2015, 9, 1089–1104. [Google Scholar] [CrossRef]
- Wang, Z.; Nasrabadi, N.; Huang, T. Spatial-spectral classification of hyperspectral images using discriminative dictionary designed by learning vector quantization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4808–4822. [Google Scholar] [CrossRef]
- Gao, L.; Yu, H.; Zhang, B.; Li, Q. Locality-preserving sparse representation-based classification in hyperspectral imagery. J. Appl. Remote Sens. 2016, 10, 1–15. [Google Scholar] [CrossRef]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-Spatial Attention Networks for Hyperspectral Image Classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Zhang, X.; Ye, Y.; Lau, R.; Lu, S.; Li, X.; Huang, X. Synergistic 2D/3D Convolutional Neural Network for Hyperspectral Image Classification. Remote Sens. 2020, 12, 2033. [Google Scholar] [CrossRef]
- Shu, K.; Wang, D. A Brief Summary of Dictionary Learning Based Approach for Classification. arXiv 2012, arXiv:1205.6544. [Google Scholar]
- Yang, M.; Zhang, L.; Yang, J.; Zhang, D. Metaface learning for sparse representation based face recognition. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010. [Google Scholar]
- Yang, M.; Zhang, L.; Feng, X.; Zhang, D. Fisher discrimination dictionary learning for sparse representation. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Coates, A.; Ng, A. The importance of encoding versus training with sparse coding and vector quantization. In Proceedings of the International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Zhang, L.; Yang, M.; Feng, X. Sparse representation or collaborative representation: Which helps face recognition? In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Projective Dictionary Pair Learning for Pattern Classification. Adv. Neural Inf. Process. Syst. 2014, 27, 793–801. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Q.; Siew, C. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Liu, X.; Deng, C.; Wang, S.; Huang, G.; Zhao, B.; Lauren, P. Fast and Accurate Spatiotemporal Fusion Based Upon Extreme Learning Machine. IEEE Geosci. Remote Sens. Lett. 2016, 13, 2039–2043. [Google Scholar] [CrossRef]
- Zhou, S.; Deng, C.; Wang, W.; Huang, G.; Zhao, B. GenELM: Generative Extreme Learning Machine feature representation. Neurocomputing 2019, 362, 41–50. [Google Scholar] [CrossRef]
- Huang, G.; Chen, L.; Siew, C. Universal Approximation Using Incremental Constructive Feedforward Networks With Random Hidden Nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Ma, L.; Jiang, H.; Zhao, H. Deep residual networks for hyperspectral image classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; Volume 142–149, pp. 1824–1827. [Google Scholar]
- Zhao, C.; Liu, W.; Xu, Y.; Wen, J. A spectral-spatial SVM-based multi-layer learning algorithm for hyperspectral image classification. Remote Sens. Lett. 2018, 9, 218–227. [Google Scholar] [CrossRef]
- Yuan, Z.; Sun, H.; Ji, K.; Zhou, H. Hyperspectral Image Classification Using Fisher Dictionary Learning based Sparse Representation. Remote Sens. Technol. Appl. 2014, 29, 646–652. [Google Scholar]
- Meng, Z.; Li, L.; Tang, X.; Feng, Z.; Jiao, L.; Liang, M. Multipath Residual Network for Spectral-Spatial Hyperspectral Image Classification. Remote Sens. 2019, 11, 1896. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Pun, C. Multi-scale hierarchical recurrent neural networks for hyperspectral image classification. Neurocomputing 2018, 294, 82–93. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Ghamisi, P.; Zhu, X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]









| Class No. | Class Name | Training | Test |
|---|---|---|---|
| 1 | Water | 6527 | 58,751 |
| 2 | Trees | 650 | 5858 |
| 3 | Asphalt | 290 | 2615 |
| 4 | Self-Blocking Bricks | 214 | 1926 |
| 5 | Bitumen | 654 | 5895 |
| 6 | Tiles | 758 | 6827 |
| 7 | Shadows | 728 | 6559 |
| 8 | Meadows | 312 | 2810 |
| 9 | Bare Soil | 216 | 1949 |
| Class No. | Class Name | Training | Test |
|---|---|---|---|
| 1 | Water | 27 | 243 |
| 2 | Hippo grass | 10 | 91 |
| 3 | Floodplain grasses 1 | 25 | 226 |
| 4 | Floodplain grassed 2 | 21 | 194 |
| 5 | Reeds | 26 | 243 |
| 6 | Riparian | 26 | 243 |
| 7 | Fire scar | 25 | 234 |
| 8 | Island interior | 20 | 183 |
| 9 | Acacia woodlands | 31 | 283 |
| 10 | Acacia shrublands | 24 | 224 |
| 11 | Acacia grasslands | 30 | 275 |
| 12 | Short mopane | 18 | 163 |
| 13 | Mixed mopane | 26 | 242 |
| 14 | Exposed soils | 9 | 86 |
| Class No. | Class Name | Training | Test |
|---|---|---|---|
| 1 | Healthy grass | 125 | 1126 |
| 2 | Stressed grass | 125 | 1129 |
| 3 | Synthetic grass | 69 | 628 |
| 4 | Tree | 124 | 1120 |
| 5 | Soil | 124 | 1118 |
| 6 | Water | 32 | 293 |
| 7 | Residential | 126 | 1142 |
| 8 | Commercial | 124 | 1120 |
| 9 | Road | 125 | 1127 |
| 10 | Highway | 122 | 1105 |
| 11 | Railway | 123 | 1112 |
| 12 | Parking Lot 1 | 123 | 1110 |
| 13 | Parking Lot 2 | 46 | 423 |
| 14 | Tennis court | 42 | 386 |
| 15 | Running track | 66 | 594 |
| Class No. | SVM | FDDL | DPL | ResNet | RNN | CNN | Ours |
|---|---|---|---|---|---|---|---|
| 1 | 0.9866 | 0.9882 | 0.9856 | 0.9845 | 0.9836 | 0.9966 | 0.9998 |
| 2 | 0.6302 | 0.2319 | 0.3743 | 0.6641 | 0.4118 | 0.7496 | 0.9507 |
| 3 | 0.9708 | 0.9851 | 0.9682 | 0.9644 | 0.9902 | 0.9669 | 0.9667 |
| 4 | 0.5055 | 0.3760 | 0.2568 | 0.4877 | 0.4646 | 0.5256 | 0.8728 |
| 5 | 0.9969 | 0.9848 | 0.9729 | 0.9835 | 0.9924 | 0.9905 | 0.9732 |
| 6 | 0.6659 | 0.6944 | 0.8576 | 0.7035 | 0.8335 | 0.9331 | 0.9534 |
| 7 | 0.9163 | 0.8811 | 0.9143 | 0.9363 | 0.9465 | 0.9503 | 0.9547 |
| 8 | 0.9416 | 0.9595 | 0.9711 | 0.9504 | 0.9794 | 0.9904 | 0.9922 |
| 9 | 0.9965 | 0.9643 | 0.9825 | 0.9895 | 0.9930 | 0.9874 | 0.9616 |
| OA | 0.9234 | 0.9057 | 0.9244 | 0.9289 | 0.9331 | 0.9663 | 0.9839 |
| AA | 0.8456 | 0.7850 | 0.8093 | 0.8515 | 0.8439 | 0.8989 | 0.9583 |
| kappa | 0.8927 | 0.8677 | 0.8937 | 0.9004 | 0.9060 | 0.9524 | 0.9723 |
| Class No. | SVM | FDDL | DPL | ResNet | RNN | CNN | Ours |
|---|---|---|---|---|---|---|---|
| 1 | 0.9465 | 0.9712 | 0.9794 | 0.9835 | 0.9346 | 0.9492 | 0.9342 |
| 2 | 1.0000 | 0.8571 | 0.9341 | 0.9890 | 0.9189 | 0.8333 | 0.8132 |
| 3 | 0.8451 | 0.7920 | 0.8496 | 0.8274 | 0.8366 | 0.9264 | 0.9735 |
| 4 | 0.8918 | 0.7887 | 0.9175 | 0.8918 | 0.7846 | 0.9323 | 0.9433 |
| 5 | 0.7037 | 0.6831 | 0.7284 | 0.7572 | 0.7704 | 0.8219 | 0.8724 |
| 6 | 0.6831 | 0.6461 | 0.6379 | 0.6214 | 0.6250 | 0.7861 | 0.8025 |
| 7 | 0.9615 | 0.7479 | 0.9316 | 0.9017 | 0.9234 | 0.9607 | 0.9573 |
| 8 | 0.8852 | 0.9126 | 0.9836 | 0.9781 | 0.8214 | 0.9005 | 0.9781 |
| 9 | 0.7279 | 0.7032 | 0.6784 | 0.7739 | 0.7651 | 0.7651 | 0.9435 |
| 10 | 0.7321 | 0.4777 | 0.8348 | 0.8527 | 0.7704 | 0.8071 | 0.9688 |
| 11 | 0.7418 | 0.7564 | 0.8945 | 0.8836 | 0.8404 | 0.8517 | 0.8691 |
| 12 | 0.9080 | 0.8037 | 0.8834 | 0.9816 | 0.7746 | 0.8580 | 0.8221 |
| 13 | 0.5785 | 0.7810 | 0.8554 | 0.7397 | 0.7371 | 0.8966 | 0.9256 |
| 14 | 0.9070 | 0.6628 | 0.7907 | 0.7907 | 0.7404 | 0.8901 | 0.9302 |
| OA | 0.8017 | 0.7515 | 0.8420 | 0.8444 | 0.8017 | 0.8676 | 0.9130 |
| AA | 0.8223 | 0.7560 | 0.8500 | 0.8552 | 0.8031 | 0.8699 | 0.9095 |
| kappa | 0.7854 | 0.7311 | 0.8289 | 0.8316 | 0.7850 | 0.8566 | 0.9057 |
| Class No. | SVM | FDDL | DPL | ResNet | RNN | CNN | Our |
|---|---|---|---|---|---|---|---|
| 1 | 0.889 | 0.9076 | 0.9831 | 0.9387 | 0.9538 | 0.9224 | 0.9645 |
| 2 | 0.9353 | 0.9477 | 0.9814 | 0.9752 | 0.9628 | 0.9824 | 0.9779 |
| 3 | 0.9586 | 0.9984 | 0.9825 | 0.9904 | 0.9857 | 0.9888 | 0.9809 |
| 4 | 0.8875 | 0.9446 | 0.8634 | 0.9598 | 0.9714 | 0.9435 | 0.9652 |
| 5 | 0.9284 | 0.9776 | 0.9902 | 0.9723 | 0.9785 | 0.9663 | 0.9821 |
| 6 | 0.8703 | 0.9829 | 0.9693 | 0.9590 | 0.9249 | 0.9691 | 0.8635 |
| 7 | 0.6261 | 0.7881 | 0.6996 | 0.7977 | 0.7820 | 0.8567 | 0.8862 |
| 8 | 0.725 | 0.5188 | 0.6571 | 0.5634 | 0.4223 | 0.7945 | 0.8429 |
| 9 | 0.551 | 0.6557 | 0.7329 | 0.7063 | 0.7045 | 0.7269 | 0.7995 |
| 10 | 0.6389 | 0.4244 | 0.8462 | 0.7747 | 0.7738 | 0.7808 | 0.7086 |
| 11 | 0.5117 | 0.4317 | 0.5926 | 0.7752 | 0.8354 | 0.7889 | 0.7707 |
| 12 | 0.5396 | 0.5315 | 0.6595 | 0.6036 | 0.7450 | 0.7348 | 0.7550 |
| 13 | 0.2766 | 0.5414 | 0.2884 | 0.6430 | 0.5745 | 0.4879 | 0.5012 |
| 14 | 0.9689 | 0.9948 | 0.9896 | 0.9896 | 0.9793 | 0.9908 | 0.9870 |
| 15 | 0.9545 | 0.9882 | 0.9848 | 0.9562 | 0.9781 | 0.9351 | 0.9815 |
| OA | 0.7409 | 0.7476 | 0.8103 | 0.8255 | 0.8280 | 0.8549 | 0.8682 |
| AA | 0.7508 | 0.7756 | 0.8147 | 0.8404 | 0.8381 | 0.8579 | 0.8644 |
| kappa | 0.7199 | 0.7271 | 0.7949 | 0.8114 | 0.8142 | 0.8431 | 0.8574 |
| Class No. | SVM | FDDL | DPL | ResNet | RNN | CNN | Ours |
|---|---|---|---|---|---|---|---|
| 1 | 0.9689 | 0.9805 | 0.8755 | 1.0000 | 0.6314 | 0.9312 | 1.0000 |
| 2 | 0.9896 | 0.7917 | 0.9896 | 0.9896 | 0.2370 | 0.7934 | 0.9063 |
| 3 | 0.6527 | 0.6862 | 0.8745 | 0.8452 | 0.7762 | 0.8779 | 0.9791 |
| 4 | 0.9122 | 0.6195 | 0.9220 | 0.8439 | 0.0714 | 0.8846 | 0.9073 |
| 5 | 0.5078 | 0.6094 | 0.7070 | 0.7891 | 0.7619 | 0.8333 | 0.8242 |
| 6 | 0.5391 | 0.5234 | 0.7070 | 0.6641 | 0.4356 | 0.7194 | 0.7500 |
| 7 | 0.8178 | 0.9474 | 0.7814 | 0.8866 | 0.8291 | 0.9551 | 0.9393 |
| 8 | 0.9016 | 0.7824 | 0.9585 | 0.9793 | 0.3591 | 0.8396 | 0.9482 |
| 9 | 0.5017 | 0.5786 | 0.7893 | 0.7525 | 0.6681 | 0.7523 | 0.8528 |
| 10 | 0.6017 | 0.7203 | 0.9110 | 0.7712 | 0.8125 | 0.7079 | 0.7839 |
| 11 | 0.8172 | 0.6276 | 0.7276 | 0.8793 | 0.8671 | 0.7595 | 0.9483 |
| 12 | 0.7209 | 0.5523 | 0.6047 | 0.9360 | 0.4409 | 0.7661 | 0.9419 |
| 13 | 0.5647 | 0.7333 | 0.9490 | 0.5765 | 0.7788 | 0.8718 | 0.7490 |
| 14 | 0.8242 | 0.9231 | 0.8132 | 0.8132 | 0.2222 | 0.7938 | 0.9231 |
| OA | 0.7125 | 0.7067 | 0.8215 | 0.8250 | 0.6122 | 0.8192 | 0.8842 |
| AA | 0.7355 | 0.7188 | 0.8293 | 0.8368 | 0.5637 | 0.8204 | 0.8895 |
| kappa | 0.6889 | 0.6827 | 0.8067 | 0.8107 | 0.5815 | 0.8042 | 0.8746 |
| Dataset | Time (s) | SVM | CNN | RNN | Ours | |
|---|---|---|---|---|---|---|
| Coding | ELM | |||||
| Pavia of | Training | 286.14 | 404.16 | 800.68 | 0.43 | 1.48 |
| Center | Testing | 6.78 | 8.21 | 9.33 | 4.50 | 0.63 |
| Botswana | Training | 51.44 | 70.03 | 296.24 | 0.03 | 0.05 |
| Testing | 1.77 | 1.9 | 3.64 | 0.13 | ||
| Houston | Training | 62.50 | 106.04 | 256.01 | 0.15 | 0.25 |
| University 2013 | Testing | 2.11 | 2.66 | 3.12 | 0.17 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhao, B.; Wang, W. An Efficient Spectral Feature Extraction Framework for Hyperspectral Images. Remote Sens. 2020, 12, 3967. https://doi.org/10.3390/rs12233967
Li Z, Zhao B, Wang W. An Efficient Spectral Feature Extraction Framework for Hyperspectral Images. Remote Sensing. 2020; 12(23):3967. https://doi.org/10.3390/rs12233967
Chicago/Turabian StyleLi, Zhen, Baojun Zhao, and Wenzheng Wang. 2020. "An Efficient Spectral Feature Extraction Framework for Hyperspectral Images" Remote Sensing 12, no. 23: 3967. https://doi.org/10.3390/rs12233967
APA StyleLi, Z., Zhao, B., & Wang, W. (2020). An Efficient Spectral Feature Extraction Framework for Hyperspectral Images. Remote Sensing, 12(23), 3967. https://doi.org/10.3390/rs12233967