Vicarious Methodologies to Assess and Improve the Quality of the Optical Remote Sensing Images: A Critical Review
Abstract
:1. Introduction
2. Image Quality of Earth Observing Satellite
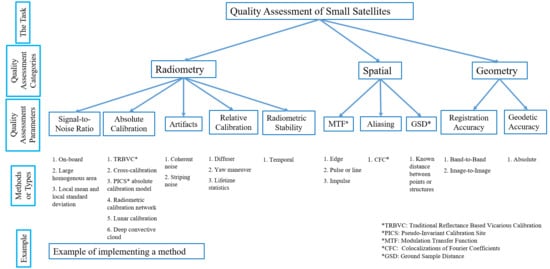
2.1. Quality Categories
2.1.1. Radiometry
2.1.2. Spatial
2.1.3. Geometry
3. Radiometric Quality Parameters and Methods
3.1. Absolute Calibration
3.1.1. PICS Absolute Calibration Model
3.1.2. Radiometric Calibration Network
- Extract RadCalNet TOA reflectance and uncertainties from the above-mentioned web portal for the same dates and times as the sensor of interest, imaging the selected site;
- Calculate test sensor TOA reflectance for the chosen site, including uncertainties;
- Interpolate the RadCalNet TOA reflectances at sensor overpass time to account for the time differences between the two measurements explained in step 1 and 2;
- In order to match the spectral resolution of the sensor to RadCalNet TOA reflectance, interpolate RadCalNet TOA reflectance (at 1 nm) to selected sensor TOA reflectance;
- Normalize RadCalNet TOA reflectance to the corresponding multispectral value of the selected sensor for direct comparisonwhere represents the relative spectral response function of the sensor of interest, is the hyperspectral TOA reflectance of RadCalNet site, and are the minimum and maximum wavelengths of the band at 10 nm steps. is the RadCalNet-predicted TOA reflectance in the specific sensor band;
- Compare the output (step 2) from the selected sensor and RadCalNet TOA Reflectance (step 5) and calculated associated uncertainties.
3.1.3. Cross-Calibration
3.1.3.1. Simultaneous Nadir Overpass (SNO) Approach
3.1.3.2. Near Coincident Observation (NCO) Approach
3.1.3.3. Spectral Response Mismatch and Uncertainty of SNO and NCO Approach
3.1.4. Traditional Reflectance-Based Vicarious Calibration
3.1.5. Lunar Calibration
3.1.6. Deep Convective Clouds
3.2. Radiometric Stability
3.2.1. Long-Term Stability
Lunar Observation-Based Method
PICS Based Radiometric Stability Monitoring
- Site selection: depending on the requirements and constraints, such as temporal stability, amount of trend to-be-detected, Lambertian nature, etc., PICS should be selected;
- TOA reflectance or radiance calculation: at sensor reflectance or radiance should be calculated using calibration parameters;
- Outlier rejection: cloud-contaminated TOA reflectance or radiance must be ignored;
- BRDF normalization: to remove the seasonality, BRDF normalization should be applied;
- Trend detection: plotting BRDF-normalized TOA reflectance or radiance and observing the change over time.
3.3. Relative Radiometric Calibration
3.3.1. Yaw or Side-Slither Maneuver
3.3.2. Lifetime Image Statistics
3.4. Signal-To-Noise Ratio
3.4.1. Homogenous Area Method
3.4.2. Local Means and Local Standard Deviations Method
3.5. Artifacts
3.5.1. Striping Noise
3.5.2. Coherent Noise
4. Spatial Quality Parameters and Methods
4.1. Modulation Transfer Function
4.1.1. Edge Method
4.1.2. Pulse or Line Method
4.1.3. Impulse Method
4.2. Aliasing
4.3. Ground Sampling Distance
5. Geometric Quality Parameters and Methods
5.1. Registration Accuracy
5.1.1. Band-to-Band Registration Accuracy
5.1.2. Image-to-Image Registration Accuracy
5.2. Geodetic Accuracy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghuffar, S. DEM generation from multi satellite PlanetScope imagery. Remote Sens. 2018, 10, 1462. [Google Scholar] [CrossRef] [Green Version]
- Dinardj, A.; Anflo, K.; Friedhoff, P. On-Orbit Commissioning of High Performance Green Propulsion (HPGP) in the SkySat Constellation. 2017. Available online: https://digitalcommons.usu.edu/smallsat/2017/all2017/139/ (accessed on 5 December 2020).
- Xue, Y.; Li, Y.; Guang, J.; Zhang, X.; Guo, J. Small satellite remote sensing and applications–history, current and future. Int. J. Remote Sens. 2008, 29, 4339–4372. [Google Scholar] [CrossRef]
- Kääb, A.; Altena, B.; Mascaro, J. Coseismic displacements of the 14 November 2016 Mw 7.8 Kaikoura, New Zealand, earthquake using the Planet optical cubesat constellation. Nat. Hazards Earth Syst. Sci. 2017, 17, 627–639. [Google Scholar]
- Jumpasut, A.; Fukuzato, A.; Greenberg, J.; Wilson, N. Lunar Radiometric Calibration on Planet Dove Satellites. 2017. Available online: https://digitalcommons.usu.edu/calcon/CALCON2017/All2017Content/27/ (accessed on 5 December 2020).
- Feng, L.; Li, J.; Gong, W.; Zhao, X.; Chen, X.; Pang, X. Radiometric cross-calibration of Gaofen-1 WFV cameras using Landsat-8 OLI images: A solution for large view angle associated problems. Remote Sens. Environ. 2016, 174, 56–68. [Google Scholar] [CrossRef]
- Helder, D.; Anderson, C.; Beckett, K.; Houborg, R.; Zuleta, I.; Boccia, V.; Clerc, S.; Kuester, M.; Markham, B.; Pagnutti, M. Observations and Recommendations for Coordinated Calibration Activities of Government and Commercial Optical Satellite Systems. Remote Sens. 2020, 12, 2468. [Google Scholar] [CrossRef]
- Weaver, O.A. An Analytical Framework for Assessing the Efficacy of Small Satellites in Performing Novel Imaging Missions. 2015. Available online: https://scholarworks.rit.edu/cgi/viewcontent.cgi?referer=https://scholar.google.com/&httpsredir=1&article=9932&context=theses (accessed on 5 December 2020).
- Pagnutti, M.; Ryan, R.E.; Kelly, M.; Holekamp, K.; Zanoni, V.; Thome, K.; Schiller, S. Radiometric characterization of IKONOS multispectral imagery. Remote Sens. Environ. 2003, 88, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Helder, D.; Coan, M.; Patrick, K.; Gaska, P. IKONOS geometric characterization. Remote Sens. Environ. 2003, 88, 69–79. [Google Scholar] [CrossRef]
- Ryan, R.; Baldridge, B.; Schowengerdt, R.A.; Choi, T.; Helder, D.L.; Blonski, S. IKONOS spatial resolution and image interpretability characterization. Remote Sens. Environ. 2003, 88, 37–52. [Google Scholar] [CrossRef] [Green Version]
- Goetz, A.; Heidebrecht, K.; Chrien, T. High Accuracy In-Flight Wavelength Calibration of Imaging Spectrometry Data. 1995. Available online: https://aviris.jpl.nasa.gov/proceedings/workshops/95_docs/20.PDF (accessed on 5 December 2020).
- Green, R.O. Spectral calibration requirement for Earth-looking imaging spectrometers in the solar-reflected spectrum. Appl. Opt. 1998, 37, 683–690. [Google Scholar] [CrossRef]
- Green, R.O. Radiative-transfer-based retrieval of reflectance from calibrated radiance imagery measured by an imaging spectrometer for lithological mapping of the Clark Mountains, California. In Imaging Spectroscopy of the Terrestrial Environment; International Society for Optics and Photonics: Washington, DC, USA, 1990; pp. 213–221. [Google Scholar]
- Barsi, J.A.; Lee, K.; Kvaran, G.; Markham, B.L.; Pedelty, J.A. The spectral response of the Landsat-8 operational land imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef] [Green Version]
- Xiong, X.; Che, N.; Barnes, W. Terra MODIS on-orbit spectral characterization and performance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2198–2206. [Google Scholar] [CrossRef]
- Mazda, F. Telecommunications Engineer’s Reference Book; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Wyatt, C. Radiometric Calibration: Theory and Methods; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Scaramuzza, P.L.; Markham, B.L.; Barsi, J.A.; Kaita, E. Landsat-7 ETM+ on-orbit reflective-band radiometric characterization. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2796–2809. [Google Scholar] [CrossRef]
- Sun, J.-Q.; Xiong, X. MODIS polarization-sensitivity analysis. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2875–2885. [Google Scholar]
- Knight, E.J.; Kvaran, G. Landsat-8 operational land imager design, characterization and performance. Remote Sens. 2014, 6, 10286–10305. [Google Scholar] [CrossRef] [Green Version]
- Operational, N.L.D.C.M. Land Imager Requirements Document–Revision, E; Nasa Goddard Space Flight Cent. GreenbeltMdUsa: Greenbelt, MD, USA, 2009. [Google Scholar]
- Holst, G.C. Electro-Optical Imaging System Performance; SPIE-International Society for Optical Engineering: Bellingham, WA, USA, 2008. [Google Scholar]
- Pratt, W.K. Digital Image Processing 1978; Willy: Hoboken, NJ, USA, 1995. [Google Scholar]
- Pillet, V.M.; Aparicio, A.; Sánchez, F. Payload and Mission Definition in Space Sciences; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Montanaro, M.; Gerace, A.; Lunsford, A.; Reuter, D. Stray light artifacts in imagery from the Landsat 8 Thermal Infrared Sensor. Remote Sens. 2014, 6, 10435–10456. [Google Scholar] [CrossRef] [Green Version]
- Dechoz, C.; Languille, F.; Tremas, T.; Nosavan, J.; Petrucci, B.; Massera, S.; Gachet, R.; Martimort, P.; Isola, C. Sentinel 2: Geometric calibration during commissioning phase. Int. Soc. Opt. Photonics 2014. [Google Scholar] [CrossRef]
- Storey, J.C.; Choate, M.J.; Meyer, D.J. A geometric performance assessment of the EO-1 advanced land imager. IEEE Trans. Geosci. Remote Sens. 2004, 42, 602–607. [Google Scholar] [CrossRef]
- Mulawa, D. On-orbit geometric calibration of the OrbView-3 high resolution imaging satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 35, 1–6. [Google Scholar]
- Dai, X.; Khorram, S. The effects of image misregistration on the accuracy of remotely sensed change detection. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1566–1577. [Google Scholar]
- Tang, Y.; Wang, Q.; Zhang, K.; Atkinson, P. Quantifying the Effect of Registration Error on Spatio-temporal Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 487–503. [Google Scholar] [CrossRef] [Green Version]
- Rao, P.N.; Roy, A.; Navalgund, R. Impact of intraband misregistration on image classification. Int. J. Geoinformatics 2005, 1, 4. [Google Scholar]
- Mishra, N.; Helder, D.; Angal, A.; Choi, J.; Xiong, X. Absolute calibration of optical satellite sensors using Libya 4 pseudo invariant calibration site. Remote Sens. 2014, 6, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Jing, X.; Leigh, L.; Teixeira Pinto, C.; Helder, D. Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors. Remote Sens. 2019, 11, 541. [Google Scholar] [CrossRef] [Green Version]
- Mishra, N.; Haque, M.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric cross calibration of Landsat 8 operational land imager (OLI) and Landsat 7 enhanced thematic mapper plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef] [Green Version]
- Dinguirard, M.; Slater, P.N. Calibration of space-multispectral imaging sensors: A review. Remote Sens. Environ. 1999, 68, 194–205. [Google Scholar] [CrossRef]
- Cramer, C. Workshop on Lunar Calibration for Satellite Remote Sensing. J. Res. Natl. Inst. Stand. Technol. 2016, 121, 367–371. [Google Scholar] [CrossRef]
- Aumann, H.; Broberg, S.; Manning, E.; Overoye, K. Using deep convective clouds identified in 16 years of AIRS infrared data for the absolute calibration and stability evaluation of the AIRS 0.4 to 1.0 micron reflected light channels. Int. Soc. Optics Photonics 2019. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, Y.; Woolliams, E.R.; Liu, Y.; Wang, N.; Wang, X.; Dai, C.; Gao, C.; Li, C.; Tang, L. Uncertainty Analysis of the Automated Radiometric Calibration over Baotou Cal&Val Site in China. In Fifth Recent Advances in Quantitative Remote Sensing; Universitat de València: Valencia, Spain, 2018; p. 211. [Google Scholar]
- Bouvet, M.; Thome, K.; Berthelot, B.; Bialek, A.; Czapla-Myers, J.; Fox, N.P.; Goryl, P.; Henry, P.; Ma, L.; Marcq, S. RadCalNet: A Radiometric Calibration Network for Earth Observing Imagers Operating in the Visible to Shortwave Infrared Spectral Range. Remote Sens. 2019, 11, 2401. [Google Scholar] [CrossRef] [Green Version]
- Leigh, L.; Shrestha, M.; Hasan, N.; Kaewmanee, M. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Site for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. 2019. Available online: https://digitalcommons.usu.edu/calcon/CALCON2019/all2019content/21/ (accessed on 8 December 2020).
- Helder, D.; Thome, K.; Aaron, D.; Leigh, L.; Czapla-Myers, J.; Leisso, N.; Biggar, S.; Anderson, N. Recent surface reflectance measurement campaigns with emphasis on best practices, SI traceability and uncertainty estimation. Metrologia 2012, 49, S21. [Google Scholar] [CrossRef] [Green Version]
- Markham, B.L.; Barsi, J.A.; Kaita, E.; Ong, L.; Morfitt, R.A.; Haque, M.O. Radiometric calibration and stability of the Landsat-8 Operational Land Imager (OLI). Int. Soc. Opt. Photonics 2015. [Google Scholar] [CrossRef]
- Chander, G.; Xiong, X.J.; Choi, T.J.; Angal, A. Monitoring on-orbit calibration stability of the Terra MODIS and Landsat 7 ETM+ sensors using pseudo-invariant test sites. Remote Sens. Environ. 2010, 114, 925–939. [Google Scholar] [CrossRef]
- Smith, D.L.; Mutlow, C.T.; Rao, C.N. Calibration monitoring of the visible and near-infrared channels of the Along-Track Scanning Radiometer-2 by use of stable terrestrial sites. Appl. Opt. 2002, 41, 515–523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D.R. Applications of spectral band adjustment factors (SBAF) for cross-calibration. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1267–1281. [Google Scholar] [CrossRef]
- Bouvet, M. Radiometric comparison of multispectral imagers over a pseudo-invariant calibration site using a reference radiometric model. Remote Sens. Environ. 2014, 140, 141–154. [Google Scholar] [CrossRef]
- Helder, D.; Thome, K.J.; Mishra, N.; Chander, G.; Xiong, X.; Angal, A.; Choi, T. Absolute radiometric calibration of Landsat using a pseudo invariant calibration site. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1360–1369. [Google Scholar] [CrossRef]
- Raut, B.; Kaewmanee, M.; Angal, A.; Xiong, X.; Helder, D. Empirical Absolute Calibration Model for Multiple Pseudo-Invariant Calibration Sites. Remote Sens. 2019, 11, 1105. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, M.; Leigh, L.; Helder, D. Classification of North Africa for Use as an Extended Pseudo Invariant Calibration Sites (EPICS) for Radiometric Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 875. [Google Scholar] [CrossRef] [Green Version]
- Xiong, X.; Sun, J.; Barnes, W.; Salomonson, V.; Esposito, J.; Erives, H.; Guenther, B. Multiyear on-orbit calibration and performance of Terra MODIS reflective solar bands. IEEE Trans. Geosci. Remote Sens. 2007, 45, 879–889. [Google Scholar] [CrossRef]
- McCorkel, J.; Thome, K.; Ong, L. Vicarious calibration of EO-1 Hyperion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 400–407. [Google Scholar] [CrossRef] [Green Version]
- Campbell, P.K.E.; Middleton, E.M.; Thome, K.J.; Kokaly, R.F.; Huemmrich, K.F.; Lagomasino, D.; Novick, K.A.; Brunsell, N.A. EO-1 hyperion reflectance time series at calibration and validation sites: Stability and sensitivity to seasonal dynamics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 276–290. [Google Scholar] [CrossRef] [Green Version]
- Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI radiometric cross comparison over desert sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
- Taylor, J.R. Error Analysis; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Helder, D.; Markham, B.; Morfitt, R.; Storey, J.; Barsi, J.; Gascon, F.; Clerc, S.; LaFrance, B.; Masek, J.; Roy, D. Observations and Recommendations for the Calibration of Landsat 8 OLI and Sentinel 2 MSI for improved data interoperability. Remote Sens. 2018, 10, 1340. [Google Scholar] [CrossRef] [Green Version]
- Czapla-Myers, J.S.; Anderson, N.J. Intercomparison of Earth-Observing Sensors Using the Radiometric Calibration Test Site (RadCaTS). In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- Liu, Y.-K.; Ma, L.-L.; Wang, N.; Qian, Y.-G.; Zhao, Y.-G.; Qiu, S.; Gao, C.-X.; Long, X.-X.; Li, C.-R. On-orbit radiometric calibration of the optical sensors on-board SuperView-1 satellite using three independent methods. Opt. Express 2020, 28, 11085–11105. [Google Scholar] [CrossRef] [PubMed]
- Alonso, K.; Bachmann, M.; Burch, K.; Carmona, E.; Cerra, D.; de los Reyes, R.; Dietrich, D.; Heiden, U.; Hölderlin, A.; Ickes, J. Data Products, Quality and Validation of the DLR Earth Sensing Imaging Spectrometer (DESIS). Sensors 2019, 19, 4471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sterckx, S.; Wolters, E. Radiometric Top-of-Atmosphere Reflectance Consistency Assessment for Landsat 8/OLI, Sentinel-2/MSI, PROBA-V, and DEIMOS-1 over Libya-4 and RadCalNet Calibration Sites. Remote Sens. 2019, 11, 2253. [Google Scholar] [CrossRef] [Green Version]
- Alhammoud, B.; Jackson, J.; Clerc, S.; Arias, M.; Bouzinac, C.; Gascon, F.; Cadau, E.G.; Iannone, R.Q.; Boccia, V. Sentinel-2 Level-1 Radiometry Assessment Using Vicarious Methods From DIMITRI Toolbox and Field Measurements From RadCalNet Database. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3470–3479. [Google Scholar] [CrossRef]
- Czapla-Myers, J.S.; Anderson, N.J. Intercomparison of the GOES-16 and-17 Advanced Baseline Imager with low-Earth orbit sensors. Int. Soc. Opt. Photonics 2019. [Google Scholar] [CrossRef]
- RadCalNet. RadCalNet Portal. Available online: www.radcalnet.org (accessed on 20 December 2019).
- Chander, G.; Meyer, D.J.; Helder, D.L. Cross calibration of the Landsat-7 ETM+ and EO-1 ALI sensor. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2821–2831. [Google Scholar] [CrossRef]
- Revel, C.; Lonjou, V.; Marcq, S.; Desjardins, C.; Fougnie, B.; Coppolani-Delle Luche, C.; Guilleminot, N.; Lacamp, A.-S.; Lourme, E.; Miquel, C. Sentinel-2A and 2B absolute calibration monitoring. Eur. J. Remote Sens. 2019, 52, 122–137. [Google Scholar] [CrossRef] [Green Version]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 operational land imager radiometric calibration and stability. Remote Sens. 2014, 6, 12275–12308. [Google Scholar] [CrossRef] [Green Version]
- Henry, P.J.; Dinguirard, M.C.; Bodilis, M. SPOT multitemporal calibration over stable desert areas. Int. Soc. Opt. Photonics 1993. [Google Scholar] [CrossRef]
- Cabor, F.; Hagolle, O.; Cosnefroy, H.; Briottet, X. Inter-calibration using desertic sites as a reference target. In Proceedings of the IGARSS′98. Sensing and Managing the Environment. 1998 IEEE International Geoscience and Remote Sensing, Seattle, WA, USA, 6–10 July 1998; pp. 2713–2715. [Google Scholar]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and characterization of Saharan and Arabian desert sites for the calibration of optical satellite sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Lacherade, S.; Fougnie, B.; Henry, P.; Gamet, P. Cross calibration over desert sites: Description, methodology, and operational implementation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1098–1113. [Google Scholar] [CrossRef]
- Thenkabail, P.S. Remote Sensing Handbook; Volume 1: Remotely Sensed Data Characterization, Classification, and Accuracies; Taylor & Francis: Oxfordshire, UK, 2016. [Google Scholar]
- Bacour, C.; Briottet, X.; Bréon, F.-M.; Viallefont-Robinet, F.; Bouvet, M. Revisiting Pseudo Invariant Calibration Sites (PICS) over sand deserts for vicarious calibration of optical imagers at 20 km and 100 km scales. Remote Sens. 2019, 11, 1166. [Google Scholar] [CrossRef] [Green Version]
- Farhad, M. Cross Calibration and Validation of Landsat 8 OLI and Sentinel 2A MSI. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2018. [Google Scholar]
- Pakat, A.; Hui, D.; Kaewmanee, M.; Helder, D.; Puangjaktha, P. Cross calibration Thaichote and Landsat 8 over Libya4 using pseudo invariant calibration sites (PICS). In Proceedings of the 2017 International Conference on Applied System Innovation (ICASI), Sapporo, Japan, 13–17 May 2017; pp. 834–837. [Google Scholar]
- Teillet, P.; Markham, B.; Irish, R.R. Landsat cross-calibration based on near simultaneous imaging of common ground targets. Remote Sens. Environ. 2006, 102, 264–270. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, M.; Hasan, M.; Leigh, L.; Helder, D. Extended Pseudo Invariant Calibration Sites (EPICS) for the Cross-Calibration of Optical Satellite Sensors. Remote Sens. 2019, 11, 1676. [Google Scholar] [CrossRef] [Green Version]
- Chander, G.; Helder, D.L.; Aaron, D.; Mishra, N.; Shrestha, A.K. Assessment of spectral, misregistration, and spatial uncertainties inherent in the cross-calibration study. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1282–1296. [Google Scholar] [CrossRef]
- Pinto, C.T.; Ponzoni, F.J.; Castro, R.M.; Leigh, L.; Kaewmanee, M.; Aaron, D.; Helder, D. Evaluation of the uncertainty in the spectral band adjustment factor (SBAF) for cross-calibration using Monte Carlo simulation. Remote Sens. Lett. 2016, 7, 837–846. [Google Scholar] [CrossRef]
- Li, S.; Ganguly, S.; Dungan, J.L.; Wang, W.; Nemani, R.R. Sentinel-2 MSI radiometric characterization and cross-calibration with Landsat-8 OLI. Adv. Remote Sens. 2017, 6, 147. [Google Scholar] [CrossRef] [Green Version]
- Thome, K.J.; Helder, D.L.; Aaron, D.; Dewald, J.D. Landsat-5 TM and Landsat-7 ETM+ absolute radiometric calibration using the reflectance-based method. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2777–2785. [Google Scholar] [CrossRef]
- Thome, K. Absolute radiometric calibration of Landsat 7 ETM+ using the reflectance-based method. Remote Sens. Environ. 2001, 78, 27–38. [Google Scholar] [CrossRef]
- Czapla-Myers, J.; McCorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Aaron, D.; Leigh, L.; Mishra, N. The ground-based absolute radiometric calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef] [Green Version]
- Thome, K.; Cattrall, C.; D’Amico, J.; Geis, J. Ground-reference calibration results for Landsat-7 ETM+. Int. Soc. Opt. Photonics 2005. [Google Scholar] [CrossRef]
- Helder, D.; Doelling, D.; Bhatt, R.; Choi, T.; Barsi, J. Calibrating Geosynchronous and Polar Orbiting Satellites: Sharing Best Practices. Remote Sens. 2020, 12, 2786. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Stone, T.C. The spectral irradiance of the Moon. Astron. J. 2005, 129, 2887. [Google Scholar] [CrossRef] [Green Version]
- Lunar Spectral Irradiance and Radiance (LUSI). Available online: https://www.nist.gov/programs-projects/lunar-spectral-irradiance-and-radiance-lusi (accessed on 27 December 2019).
- Adriaensen, S.; Bouvet, M.; Woolliams, E.; Taylor, S.; Miranda, M.G.; Toledano, C.; Berjón, A.; Baretto, Á. Lunar Irradiance Measurement and Modelling. Available online: http://gsics.atmos.umd.edu/pub/Development/AnnualMeeting2019/4g_Adriaensen_Lunar_Calibration_Measurements_Modelling.pptx (accessed on 31 December 2019).
- Stone, T.C. Lunar Observations Planning for CLARREO. Available online: https://clarreo.larc.nasa.gov/2016-05STM/Wednesday/Stone_CLARREO_SDT_Spring2016.pdf (accessed on 27 December 2019).
- Doelling, D.R.; Morstad, D.; Scarino, B.R.; Bhatt, R.; Gopalan, A. The characterization of deep convective clouds as an invariant calibration target and as a visible calibration technique. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1147–1159. [Google Scholar] [CrossRef]
- Sohn, B.; Ham, S.-H.; Yang, P. Possibility of the visible-channel calibration using deep convective clouds overshooting the TTL. J. Appl. Meteorol. Climatol. 2009, 48, 2271–2283. [Google Scholar] [CrossRef]
- Doelling, D.R.; Nguyen, L.; Minnis, P. On the use of deep convective clouds to calibrate AVHRR data. Int. Soc. Opt. Photonics 2004, 281–289. [Google Scholar] [CrossRef] [Green Version]
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) radiometric performance on-orbit. Remote Sens. 2015, 7, 2208–2237. [Google Scholar] [CrossRef] [Green Version]
- Angal, A.; Xiong, X.; Helder, D.; Kaewmanee, M.; Leigh, L. Assessing the calibration differences in the reflective solar bands of Terra MODIS and Landsat-7 enhanced thematic mapper plus. J. Appl. Remote Sens. 2018, 12, 044002. [Google Scholar] [CrossRef]
- Barsi, J.A.; Markham, B.L.; Helder, D.L. Continued monitoring of Landsat reflective band calibration using pseudo-invariant calibration sites. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 7007–7010. [Google Scholar]
- Markham, B.L.; Barker, J.L.; Barsi, J.A.; Kaita, E.; Thome, K.J.; Helder, D.L.; Palluconi, F.D.; Schott, J.R.; Scaramuzza, P. Landsat-7 ETM+ radiometric stability and absolute calibration. Int. Soc. Opt. Photonics 2003, 4881, 308–318. [Google Scholar]
- Zanter, K. Landsat 8 (L8) Data Users Handbook. Landsat Sci. Off. Website 2016. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwinj7bMsrjtAhUKfXAKHZmsBpEQFjAAegQIAxAC&url=https%3A%2F%2Fprd-wret.s3-us-west-2.amazonaws.com%2Fassets%2Fpalladium%2Fproduction%2Fatoms%2Ffiles%2FLSDS-1574_L8_Data_Users_Handbook-v5.0.pdf&usg=AOvVaw1ZXuC-Pou3iCck8Tb1N_mp (accessed on 5 December 2020).
- Helder, D.L.; Ruggles, T.A.; Dewald, J.D.; Madhavan, S. Landsat-5 Thematic Mapper reflective-band radiometric stability. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2730–2746. [Google Scholar] [CrossRef]
- Kaewmanee, M. Pseudo Invariant Calibration Sites: PICS Evolution; Utah State University: Logan, UT, USA, 2018. [Google Scholar]
- Barsi, J.A.; Markham, B.L.; Czapla-Myers, J.S.; Helder, D.L.; Hook, S.J.; Schott, J.R.; Haque, M.O. Landsat-7 ETM+ radiometric calibration status. Int. Soc. Opt. Photonics 2016, 9972, 99720C. [Google Scholar]
- Markham, B.L.; Thome, K.J.; Barsi, J.A.; Kaita, E.; Helder, D.L.; Barker, J.L.; Scaramuzza, P.L. Landsat-7 ETM+ on-orbit reflective-band radiometric stability and absolute calibration. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2810–2820. [Google Scholar] [CrossRef]
- Sterckx, S.; Adriaensen, S.; Dierckx, W.; Bouvet, M. In-Orbit Radiometric Calibration and Stability Monitoring of the PROBA-V Instrument. Remote Sens. 2016, 8, 546. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.-Q.; Xiong, X.; Barnes, W.L.; Guenther, B. MODIS reflective solar bands on-orbit lunar calibration. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2383–2393. [Google Scholar] [CrossRef]
- Eplee Jr, R.E.; Barnes, R.A.; Patt, F.S.; Meister, G.; McClain, C.R. SeaWiFS lunar calibration methodology after six years on orbit. Int. Soc. Opt. Photonics 2004, 5542, 1–13. [Google Scholar]
- Teillet, P.; Barsi, J.; Chander, G.; Thome, K. Prime candidate earth targets for the post-launch radiometric calibration of space-based optical imaging instruments. Int. Soc. Opt. Photonics 2007, 6677, 66770S. [Google Scholar]
- Teillet, P.; Chander, G. Terrestrial reference standard sites for postlaunch sensor calibration. Can. J. Remote Sens. 2010, 36, 437–450. [Google Scholar] [CrossRef]
- Chander, G. Catalog of Worldwide Test Sites for Sensor Characterization. Us Geol. Surv. 2009. Available online: https://pubs.er.usgs.gov/publication/70033320 (accessed on 5 December 2020).
- Kim, W.; He, T.; Wang, D.; Cao, C.; Liang, S. Assessment of long-term sensor radiometric degradation using time series analysis. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2960–2976. [Google Scholar] [CrossRef]
- Angal, A.; Xiong, X.; Choi, T.; Chander, G.; Wu, A. Using the Sonoran and Libyan Desert test sites to monitor the temporal stability of reflective solar bands for Landsat 7 enhanced thematic mapper plus and Terra moderate resolution imaging spectroradiometer sensors. J. Appl. Remote Sens. 2010, 4, 043525. [Google Scholar]
- Helder, D.L.; Markham, B.L.; Thome, K.J.; Barsi, J.A.; Chander, G.; Malla, R. Updated radiometric calibration for the Landsat-5 Thematic Mapper reflective bands. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3309–3325. [Google Scholar] [CrossRef]
- Helder, D.L.; Basnet, B.; Morstad, D.L. Optimized identification of worldwide radiometric pseudo-invariant calibration sites. Can. J. Remote Sens. 2010, 36, 527–539. [Google Scholar] [CrossRef]
- Tabassum, R. Worldwide Optimal PICS Search. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2017. [Google Scholar]
- Hasan, M.N.; Shrestha, M.; Leigh, L.; Helder, D. Evaluation of an Extended PICS (EPICS) for Calibration and Stability Monitoring of Optical Satellite Sensors. Remote Sens. 2019, 11, 1755. [Google Scholar] [CrossRef] [Green Version]
- Chander, G.; Christopherson, J.; Stensaas, G.; Teillet, P. Online catalog of world-wide test sites for the post-launch characterization and calibration of optical sensors. In Proceedings of the 58th International Astronautical Congress 2007, Hyderabad, India, 24–27 September 2007; pp. 2043–2051. [Google Scholar]
- Castracane, P. PICS: Pseudo-Invariant Calibration Sites. Available online: http://calvalportal.ceos.org/tools/impetus/-/asset_publisher/fR59YEK8GYhK/content/pics-pseudo-invariant-calibration-sites;jsessionid=17CD9AD300A60C4DA9EDA661DE4D061D (accessed on 5 December 2020).
- Magellium, C.A. CEOS WGCV IVOS Initiative on the Characterization of PICS. Available online: https://picscar.magellium.com/# (accessed on 5 December 2020).
- Tuli, F.T.Z.; Pinto, C.T.; Angal, A.; Xiong, X.; Helder, D. New Approach for Temporal Stability Evaluation of Pseudo-Invariant Calibration Sites (PICS). Remote Sens. 2019, 11, 1502. [Google Scholar] [CrossRef] [Green Version]
- Vuppula, H. Normalization of Pseudo-Invariant Calibration Sites for Increasing the Temporal Resolution and Long-Term Trending. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2017. [Google Scholar]
- Tiao, G.C.; Reinsel, G.C.; Xu, D.; Pedrick, J.; Zhu, X.; Miller, A.; DeLuisi, J.; Mateer, C.; Wuebbles, D. Effects of autocorrelation and temporal sampling schemes on estimates of trend and spatial correlation. J. Geophys. Res. Atmos. 1990, 95, 20507–20517. [Google Scholar] [CrossRef]
- Spooner, J.; Dressing, S.; Meals, D. Minimum Detectable Change Analysis. Environ. Prot. Agency 2011. Available online: https://www.epa.gov/sites/production/files/2016-05/documents/tech_notes_7_dec_2013_mdc.pdf (accessed on 5 December 2020).
- Waldner, P.; Marchetto, A.; Thimonier, A.; Schmitt, M.; Rogora, M.; Granke, O.; Mues, V.; Hansen, K.; Karlsson, G.P.; Žlindra, D. Detection of temporal trends in atmospheric deposition of inorganic nitrogen and sulphate to forests in Europe. Atmos. Environ. 2014, 95, 363–374. [Google Scholar] [CrossRef] [Green Version]
- Weatherhead, E.C.; Reinsel, G.C.; Tiao, G.C.; Meng, X.L.; Choi, D.; Cheang, W.K.; Keller, T.; DeLuisi, J.; Wuebbles, D.J.; Kerr, J.B. Factors affecting the detection of trends: Statistical considerations and applications to environmental data. J. Geophys. Res. Atmos. 1998, 103, 17149–17161. [Google Scholar] [CrossRef]
- Weatherhead, E.C.; Reinsel, G.C.; Tiao, G.C.; Jackman, C.H.; Bishop, L.; Frith, S.M.H.; DeLuisi, J.; Keller, T.; Oltmans, S.J.; Fleming, E.L. Detecting the recovery of total column ozone. J. Geophys. Res. Atmos. 2000, 105, 22201–22210. [Google Scholar] [CrossRef] [Green Version]
- Bhatt, R.; Doelling, D.R.; Wu, A.; Xiong, X.; Scarino, B.R.; Haney, C.O.; Gopalan, A. Initial stability assessment of S-NPP VIIRS reflective solar band calibration using invariant desert and deep convective cloud targets. Remote Sens. 2014, 6, 2809–2826. [Google Scholar] [CrossRef] [Green Version]
- Mendenhall, J.; Bernotas, L.; Bicknell, W.; Cerrati, V.; Digenis, C.; Evans, J.; Forman, S.; Hearn, D.; Hoffeld, R.; Lencioni, D. Earth Observing-1 Advanced Land Imager: Instrument and flight operations overview. Mass. Inst. Technol. Linc. Lab. Proj. Rep. Eo 2000, 1, 121. [Google Scholar]
- Anderson, C.; Naughton, D.; Brunn, A.; Thiele, M. Radiometric correction of RapidEye imagery using the on-orbit side-slither method. Int. Soc. Opt. Photonics 2011, 8180, 818008. [Google Scholar]
- Angal, A.; Helder, D. Advanced Land Imager Relative Gain Characterization and Correction; Electrical Engineering and Computer Science Department: Brookings, SD, USA, 2005. [Google Scholar]
- Krause, K.S. Relative radiometric characterization and performance of the QuickBird high-resolution commercial imaging satellite. Int. Soc. Opt. Photonics 2004, 5542, 35–44. [Google Scholar]
- Pesta, F.; Bhatta, S.; Helder, D.; Mishra, N. Radiometric non-uniformity characterization and correction of landsat 8 oli using earth imagery-based techniques. Remote Sens. 2015, 7, 430–446. [Google Scholar] [CrossRef] [Green Version]
- Henderson, B.G.; Krause, K.S. Relative radiometric correction of QuickBird imagery using the side-slither technique on orbit. Int. Soc. Opt. Photonics 2004, 5542, 426–436. [Google Scholar]
- Li, H.; Man, Y.-Y. Relative radiometric calibration method based on linear CCD imaging the same region of non-uniform scene. Int. Soc. Opt. Photonics 2014, 9299, 929906. [Google Scholar]
- Wang, M.; Chen, C.; Pan, J.; Zhu, Y.; Chang, X. A Relative Radiometric Calibration Method Based on the Histogram of Side-Slither Data for High-Resolution Optical Satellite Imagery. Remote Sens. 2018, 10, 381. [Google Scholar] [CrossRef] [Green Version]
- Kubik, P.; Pascal, V. Amethist: A method for equalization thanks to histograms. Int. Soc. Opt. Photonics 2004, 5570, 256–267. [Google Scholar]
- Pesta, F. Relative Radiometic Characterization and Correction of the Landsat 8 OLI Using the On-Orbit Side-Slither Maneuver. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2015. [Google Scholar]
- Shrestha, A.K. Relative Gain Characterization and Correction for Pushbroom Sensors Based on Lifetime Image Statistics and Wavelet Filtering. Ph.D. Thesis, Electrical Engineering and Computer Science Department, South Dakota State University, Brookings, SD, USA, 2010. [Google Scholar]
- Anderson, C.; Helder, D.L.; Jeno, D. Statistical relative gain calculation for Landsat 8. Int. Soc. Opt. Photonics 2017, 10402, 104021F. [Google Scholar]
- Amit Angal, D.D.H. Advanced Land Imager Relative Gain Characterization and Correction. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2005. [Google Scholar]
- Micijevic, E.; Vanderwerff, K.; Scaramuzza, P.; Morfitt, R.A.; Barsi, J.A.; Levy, R. On-orbit performance of the Landsat 8 Operational Land Imager. Int. Soc. Opt. Photonics 2014, 9218, 921816. [Google Scholar]
- Markham, B.L.; Barker, J.; Kaita, E.; Seiferth, J.; Morfitt, R. On-orbit performance of the Landsat-7 ETM+ radiometric calibrators. Int. J. Remote Sens. 2003, 24, 265–285. [Google Scholar] [CrossRef]
- Xiong, X.; Angal, A.; Xie, X. On-orbit noise characterization for MODIS reflective solar bands. In Proceedings of the IGARSS 2008–2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar] [CrossRef] [Green Version]
- Van der Meer, F.D.; De Jong, S.M. Imaging Spectrometry: Basic Principles and Prospective Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 4. [Google Scholar]
- Gao, B.-C. An operational method for estimating signal to noise ratios from data acquired with imaging spectrometers. Remote Sens. Environ. 1993, 43, 23–33. [Google Scholar] [CrossRef]
- Ren, H.; Du, C.; Liu, R.; Qin, Q.; Yan, G.; Li, Z.-L.; Meng, J. Noise evaluation of early images for Landsat 8 Operational Land Imager. Opt. Express 2014, 22, 27270–27280. [Google Scholar] [CrossRef] [PubMed]
- Fujimotor, N.; Takahashi, Y.; Moriyama, T.; Shimada, M.; Wakabayashi, H.; Nakatani, Y.; Obayashi, S. Evaluation of SPOT HRV image data received in Japan. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; pp. 463–466. [Google Scholar]
- Jiang, B.; Liang, S.; Townshend, J.R.; Dodson, Z.M. Assessment of the radiometric performance of Chinese HJ-1 satellite CCD instruments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 840–850. [Google Scholar] [CrossRef]
- Piscini, A.; Amici, S. Estimation of Signal to Noise Ratio for Unsupervised Hyperspectral Images. Quad. Di Geofis. 2010. Available online: http://istituto.ingv.it/images/collane-editoriali/quaderni-di-geofisica/quaderni-di-geofisica-2010/Quaderno78.pdf (accessed on 5 December 2020).
- Li, J.; Chen, X.; Tian, L.; Huang, J.; Feng, L. Improved capabilities of the Chinese high-resolution remote sensing satellite GF-1 for monitoring suspended particulate matter (SPM) in inland waters: Radiometric and spatial considerations. Isprs J. Photogramm. Remote Sens. 2015, 106, 145–156. [Google Scholar] [CrossRef]
- Lee, J.; Hoppel, K. Noise modeling and estimation of remotely-sensed images. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; pp. 1005–1008. [Google Scholar]
- Zhang, H.; Li, J.; Huang, Y.; Zhang, L. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 2056–2065. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recognit. 2010, 43, 2367–2379. [Google Scholar] [CrossRef] [Green Version]
- Iordache, M.-D.; Bioucas-Dias, J.M.; Plaza, A. Collaborative sparse regression for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2013, 52, 341–354. [Google Scholar] [CrossRef] [Green Version]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. Isprs J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.-Z.; Zhao, X.-L.; Deng, L.-J.; Huang, J. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sens. 2017, 9, 559. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Yan, L.; Wu, T.; Zhong, S. Remote sensing image stripe noise removal: From image decomposition perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar] [CrossRef]
- Liu, J.G.; Morgan, G.L.K. FFT selective and adaptive filtering for removal of systematic noise in ETM+ imageodesy images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3716–3724. [Google Scholar] [CrossRef]
- USGS. Landsat Known Issues-Coherent Noise. Available online: https://www.usgs.gov/landresources/nli/landsat/coherent-noise?qt-science_support_page_related_con=0#qtscience_support_page_related_con (accessed on 13 March 2020).
- Amraei, E.; Mobasheri, M.R. Coherent Noise Removal in Dark pixels (Case Study: Images Acquired By Landsat 5 Thematic Mapper). Int. J. Innov. Sci. Eng. Technol. 2014, 1, 235–243. [Google Scholar]
- Nichol, J.; Vohora, V. Noise over water surfaces in Landsat TM images. Int. J. Remote Sens. 2004, 25, 2087–2093. [Google Scholar] [CrossRef]
- Tilton, J.C.; Markham, B.L.; Alford, W.L. Landsat-4 and Landsat-5 MSS Coherent Noise: Characterization and Removal. Photogramm. Eng. Remote Sens. 1985, 51, 1263–1279. [Google Scholar]
- Helder, D.L.; Ruggles, T.A. Landsat thematic mapper reflective-band radiometric artifacts. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2704–2716. [Google Scholar] [CrossRef]
- Pedelty, J.A.; Markham, B.L.; Barker, J.L.; Seiferth, J.C. Pre-launch noise characterization of the Landsat-7 Enhanced Thematic Mapper Plus (ETM Plus). Int. Soc. Opt. Photonics 1999, 3750, 376–387. [Google Scholar]
- Crespi, M.; De Vendictis, L. A procedure for high resolution satellite imagery quality assessment. Sensors 2009, 9, 3289–3313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, T.; Helder, D.L. Generic sensor modeling for modulation transfer function (MTF) estimation. Pecora 2005, 16, 23–27. [Google Scholar]
- Helde, D.; Choi, J.; Anderson, C. On-Orbit Modulation Transfer Function (MTF) Measurements for IKONOS and QuickBird; South Dakota State: Brookings, SD, USA, 2007. [Google Scholar]
- Schowengerdt, R.; Archwamety, C.; Wrigley, R.C. Operational MTF for Landsat thematic mapper. Int. Soc. Opt. Photonics 1985, 549, 110–118. [Google Scholar]
- Helder, D.; Choi, T.; Rangaswamy, M. In-flight characterization of spatial quality using point spread functions. In Post-Launch Calibration of Satellite Sensors; CRC Press: Boca Raton, FL, USA, 2004; pp. 159–198. [Google Scholar]
- Kohm, K. Modulation Transfer Function Measurement Method and Results for the Orbview-3 High Resolution Imaging Satellite. In Proceedings of ISPRS; 2004; pp. 12–23. Available online: https://www.isprs.org/proceedings/XXXV/congress/comm1/papers/2.pdf (accessed on 5 December 2020).
- Berthelot, B.; Santer, R.; Blanc, R.; Saunier, S.; Kocaman, S. Calibration Test Sites Selection and Characterisation–WP210. Vega Technol. Sas. Fr. 2008. Available online: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwi9noWWsLjtAhVEX60KHX7iB-oQFjAAegQIBBAC&url=http%3A%2F%2Fcalvalportal.ceos.org%2Fc%2Fdocument_library%2Fget_file%3Fuuid%3D03407bb4-89e4-4271-be26-898298780ee7%26groupId%3D10136&usg=AOvVaw0NRSh3BLE4WRn7zwpOnFdf (accessed on 5 December 2020).
- Choi, T.; Xiong, X.; Wang, Z. On-orbit lunar modulation transfer function measurements for the moderate resolution imaging spectroradiometer. IEEE Trans. Geosci. Remote Sens. 2013, 52, 270–277. [Google Scholar] [CrossRef] [Green Version]
- Viallefont-Robinet, F.; Léger, D. Improvement of the edge method for on-orbit MTF measurement. Opt. Express 2010, 18, 3531–3545. [Google Scholar] [CrossRef]
- Nelson, N.R.; Barry, P. Measurement of Hyperion MTF from on-orbit scenes. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No. 01CH37217), Sydney, NSW, Australia, 9–13 July 2001; pp. 2967–2969. [Google Scholar]
- Helder, D.; Choi, J. On-Orbit Modulation Transfer Function (mtf) Measurement of Quickbird; South Dakota State University: Brookings, SD, USA, 2006. [Google Scholar]
- Wang, Z.; Xiong, X. VIIRS on-orbit spatial characterization using the Moon. IEEE Geosci. Remote Sens. Lett. 2013, 11, 1116–1120. [Google Scholar] [CrossRef]
- Wang, Z.; Xiong, X.; Choi, T.; Link, D. On-orbit characterization of MODIS modulation transfer function using the moon. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4112–4121. [Google Scholar] [CrossRef]
- Shea, J.J. Lunar limb knife-edge optical transfer function measurements. J. Electron. Imaging 1999, 8, 196–209. [Google Scholar] [CrossRef]
- USGS. Test Sites Catalog. Available online: https://calval.cr.usgs.gov/apps/test_sites_catalog (accessed on 20 March 2020).
- Xu, M.; Cong, M.; Li, H. Research of on-orbit MTF measurement for the satellite sensors. Int. Soc. Opt. Photonics 2014, 9158, 915809. [Google Scholar]
- Helder, D.; Choi, T.; Rangaswamy, M. Quickbird Satellite In-Orbit Modulation Transfer Function (MTF) Measurement Using Edge, Pulse and Impulse Methods for Summer 2003. 2005. Available online: https://www.amazon.com/Quickbird-Satellite-Modulation-Transfer-Measurement-ebook/dp/B07WTPKW3J (accessed on 5 December 2020).
- USGS. Edge MTF Target. Available online: https://calval.cr.usgs.gov/apps/salon-de-provence-france-mtf-site (accessed on 20 March 2020).
- Storey, J.C. Landsat 7 on-orbit modulation transfer function estimation. Int. Soc. Opt. Photonics 2001, 4540, 50–61. [Google Scholar]
- Hearn, D.R. Earth Observing-1 Advanced Land Imager: Imaging Performance On-Orbit; Massachusetts Inst of Tech Lexington Lincoln Lab.: Lexington, MA, USA, 2002. [Google Scholar]
- Meygret, A.; Blanchet, G.; Latry, C.; Kelbert, A.; Gross-Colzy, L. On-Orbit Star-Based Calibration and Modulation Transfer Function Measurements for PLEIADES High-Resolution Optical Sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5525–5534. [Google Scholar] [CrossRef]
- Leger, D.; Viallefont, F.; Hillairet, E.; Meygret, A. In-flight refocusing and MTF assessment of SPOT5 HRG and HRS cameras. Int. Soc. Opt. Photonics 2003, 4881, 224–231. [Google Scholar]
- Leger, D.; Duffaut, J.; Robinet, F. MTF measurement using spotlight. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; pp. 2010–2012. [Google Scholar]
- Fourest, S.; Kubik, P.; Lebègue, L.; Déchoz, C.; Lacherade, S.; Blanchet, G. Star-based methods for Pleiades HR commissioning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2012, 39, 513–518. [Google Scholar] [CrossRef] [Green Version]
- Kang, C.-H.; Chung, J.-H.; Kim, Y.-H. On-orbit MTF estimation for the KOMPSAT-3 satellite using star images. Remote Sens. Lett. 2015, 6, 1002–1011. [Google Scholar] [CrossRef]
- Faran, S.; Eshet, I.; Yehezkel, N.; Molcho, J. Estimation of the MTF of a satellite imaging-system from celestial scenes. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Rangaswamy, M. Two-Dimensional on-orbit Modulation Transfer Function Analysis Using Convex Mirror Array. Master’s Thesis, South Dakota State University, Brookings, SD, USA, 2003; pp. 30–69. [Google Scholar]
- Barducci, A.; Baronti, S.; Bonsignori, R.; Capanni, A.; Del Bello, U.; Marcoionni, P.; Pippi, I.; Romoli, A.; Santurri, L.; Vitulli, R. Aliasing effects on images acquired by hyperspectral pushbroom sensors. Int. Soc. Opt. Photonics 2001, 4540, 135–146. [Google Scholar]
- Chae, E.; Lee, E.; Kang, W.; Cheong, H.; Paik, J. Spatially adaptive antialiasing for enhancement of mobile imaging system using combined wavelet-Fourier transform. IEEE Trans. Consum. Electron. 2013, 59, 862–868. [Google Scholar] [CrossRef]
- Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A theoretical analysis of the effects of aliasing and misregistration on pansharpened imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
- Geiger, C.; Müller, H.-R.; Samluk, J.P.; Bernstein, E.R.; Richter-Menge, J. Impact of spatial aliasing on sea-ice thickness measurements. Ann. Glaciol. 2015, 56, 353–362. [Google Scholar] [CrossRef] [Green Version]
- Schowengerdt, R.A. Aliasing in remote sensing imagery. Int. Soc. Opt. Photonics 2002, 4736, 92–98. [Google Scholar]
- Coulange, B.; Moisan, L. An aliasing detection algorithm based on suspicious colocalizations of fourier coefficients. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 2013–2016. [Google Scholar]
- Vandewalle, P.; Süsstrunk, S.; Vetterli, M. A frequency domain approach to registration of aliased images with application to super-resolution. Eurasip J. Adv. Signal Process. 2006, 2006, 071459. [Google Scholar] [CrossRef] [Green Version]
- Chae, E.; Lee, E.; Kang, W.; Lim, Y.; Jung, J.; Kim, T.; Katsaggelos, A.K.; Paik, J. Frequency-domain analysis of discrete wavelet transform coefficients and their adaptive shrinkage for anti-aliasing. In Proceedings of the 2013 IEEE International Conference on Image Processing, Melbourne, VIC, Australia, 15–18 September 2013; pp. 1071–1074. [Google Scholar]
- Valenzuela, Á.Q.; Reyes, J.C.G. Basic Spatial Resolution Metrics for Satellite Imagers. IEEE Sens. J. 2019, 19, 4914–4922. [Google Scholar] [CrossRef]
- Leachtenauer, J.C.; Driggers, R.G. Surveillance and Reconnaissance Imaging Systems: Modeling and Performance Prediction; Artech House: Norwood, MA, USA, 2001. [Google Scholar]
- USGS. Guide to Digital Imagery Spatial Resolution; USGS: Reston, VA, USA, 2018. [Google Scholar]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Xiong, X.; Qu, J.J.; Che, N.; Summers, M.E. Impact analysis of MODIS band-to-band registration on its measurements and science data products. Int. J. Remote Sens. 2011, 32, 4431–4444. [Google Scholar] [CrossRef]
- Xiong, X.; Che, N.; Barnes, W. Terra MODIS on-orbit spatial characterization and performance. IEEE Trans. Geosci. Remote Sens. 2005, 43, 355–365. [Google Scholar] [CrossRef]
- Xie, Y.; Xiong, X.; Qu, J.J.; Che, N.; Wang, L. MODIS on-orbit spatial characterization results using ground measurements. Int. Soc. Opt. Photonics 2006, 6296, 62961L. [Google Scholar]
- Choi, T.; Shao, X.; Cao, C. NOAA-20 Visible Infrared Imaging Radiometer Suite (VIIRS) on-Orbit Band-To-Band Registration Estimation for Reflective Solar Band (RSB) Using Scheduled Lunar Collections. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 9059–9062. [Google Scholar]
- Wang, Z.; Xiong, X.; Li, Y. Improved band-to-band registration characterization for VIIRS reflective solar bands based on lunar observations. Remote Sens. 2016, 8, 27. [Google Scholar] [CrossRef] [Green Version]
- Xiong, X.; Sun, J.; Xiong, S.; Barnes, W.L. Using the moon for MODIS on-orbit spatial characterization. Int. Soc. Opt. Photonics 2004, 5234, 480–487. [Google Scholar]
- Gruen, A. Development and status of image matching in photogrammetry. Photogramm. Rec. 2012, 27, 36–57. [Google Scholar] [CrossRef]
- Storey, J.; Choate, M.; Lee, K. Landsat 8 Operational Land Imager on-orbit geometric calibration and performance. Remote Sens. 2014, 6, 11127–11152. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.S.; Storey, J.C.; Choate, M.J.; Hayes, R.W. Four years of Landsat-7 on-orbit geometric calibration and performance. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2786–2795. [Google Scholar] [CrossRef]
- Pratt, W.K. Correlation techniques of image registration. IEEE Trans. Aerosp. Electron. Syst. 1974, 353–358. [Google Scholar] [CrossRef]
- Li, H.; Manjunath, B.; Mitra, S.K. A contour-based approach to multisensor image registration. IEEE Trans. Image Process. 1995, 4, 320–334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tseng, Y.-H.; Tzen, J.-J.; Tang, K.-P.; Lin, S.-H. Image-to-image registration by matching area features using Fourier descriptors and neural networks. Photogramm. Eng. Remote Sens. 1997, 63, 975–983. [Google Scholar]
- Gao, F.; Masek, J.G.; Wolfe, R.E. Automated registration and orthorectification package for Landsat and Landsat-like data processing. J. Appl. Remote Sens. 2009, 3, 033515. [Google Scholar]
- USGS. Geometric Calibration Sites. Available online: https://calval.cr.usgs.gov/apps/usgs-eros-range (accessed on 3 March 2020).











| Methods | Strengths | Weaknesses | Traceability |
|---|---|---|---|
| Absolute Pseudo-Invariant Calibration Sites (APICS) and/or Extended Pseudo-Invariant Calibration Sites Absolute Calibration (ExPAC) Model [33,41] | Easy to implement Inexpensive Low atmospheric effect Stable Homogenous surface | Requires Pseudo-Invariant Calibration Sites (PICS) and/or Extended PICS (EPICS) data | APICS—2–3% accuracy and 1–2% precision ExPAC—1–2% accuracy (Visible to Shortwave Infrared bands) and 1–2% precision |
| Radiometric Calibration Network (RadCalNet) [34,40] | Open data Spatially homogenous site High temporal resolution Quality-controlled and processed top-of-the-atmosphere (TOA) reflectance data | Fixed location Requires images of RadCalNet site Bidirectional reflectance distribution function (BRDF) effect not accounted for | Railroad Valley— 3–4% uncertainty La Crau— 2–6% uncertainty Gababeb— 3–4% uncertainty Baotou—4–4.5% uncertainty |
| Cross-Calibration [35] | Inexpensive Open data from well-calibrated sensor Multiple well-calibrated sensors are on-orbit | Simultaneous nadir overpass (SNO) approach requires concurrent scenes with well-calibrated sensor Near coincident observation (NCO) approach requires scenes over stable target, which can be harder to find in the Earth surface Multiple sources of uncertainty | Uncertainty will vary depending on the ‘reference’ sensor, number of observation, atmosphere, spectral response mismatch, scene pairs are SNO or NCO, etc. |
| Traditional Reflectance-based Vicarious Calibration (TRBVC) [36,42] | Appropriately modeled atmospheric condition can give low uncertainty of measurement Independent method for calibrating satellite sensor (similar to instrumented RadCalNet approach but calibration can be performed over vegetative, desert, etc., target) | Expensive due to the requirement of experienced field personnel and instrument Requires good ground instrument and ability to measure atmospheric conditions accurately Lengthy process | 1.5% to 2.5% uncertainty |
| Lunar Calibration [37] | Stable No Atmosphere | Imaging direction must be altered Satellite should be able to point the lunar surface and collect imagery | 5–10% uncertainty of United States Geological Survey (USGS) lunar calibration model |
| Deep Convective Cloud (DCC) [38] | Near Lambertian Little Atmosphere | Difficult to find right type of cloudy image Works best for shorter wavelength channels | About 5% uncertainty |
| Satellite | Accuracy | Spatial Resolution | Temporal Resolution |
|---|---|---|---|
| MODIS | ~2% | 250m to 1000m | 1 to 2 days |
| Sentinel 2A, 2B | <3% to 5% | 10m | 5 days |
| Landsat 7 | ~5% | 30m | 16 days |
| Landsat 8 | <3% | 30m | 16 days |
| Methods | Strengths | Weaknesses | Target Type |
|---|---|---|---|
| Yaw or Side-Slither Maneuver [125,127,128,129] | Can be time-efficient compared to statistics approach One cloud-free acquisition may be enough | Satellite should have the ability to maneuver Loss of normal image data Requires uniform imaging target | Visible and near-inferred band: Greenland and Dome C of Antarctica SWIR band: Sahara Desert and Arabian Peninsula sites |
| Lifetime Statistics [126] | No need to maneuver Normal Earth-scene-based approach | Requires substantial number of images | Any surface type |
| Methods | Strengths | Weaknesses | Target Type |
|---|---|---|---|
| Homogenous Area [140,142] | Relatively easy to compute Normal Earth scene can be used | Almost impossible to find absolute homogenous surface in satellite imagery | dry lake, desert, snow, dense vegetation |
| Local Mean and Local Standard Deviation [141] | Can be automated Does not require large homogenous areas but many small homogenous regions. | Noise must be mainly additive Image should contain many small homogenous areas | Target with many small homogenous areas |
| Methods | Strengths | Weaknesses | Target Type |
|---|---|---|---|
| Edge [163] | Edge target can be found in the normal imagery | Edge profile should be homogenous Edge should be straight, otherwise edge alignment will be necessary | Artificial edge: painted checkerboard, tarp-made, parking lot, etc. Natural edge: Agricultural field boundaries, moon, sea/icefield transition, etc. |
| Pulse or Line [164,165] | Line spread function (LSF) can be obtained directly from the sensor output | Requires knowledge of target width Homogeneity must be maintained throughout the pulse | Bridges can be used as target for moderate spatial resolution sensor (from 10 to 60m) |
| Impulse [166] | Provide a full 2D estimate of Point Spread Function (PSF) Relatively easy to calculate MTF | Point target and surrounding area must be uniform Several point sources are needed to obtain full 2D PSF | Artificial target: convex mirror, spotlights, etc. Natural target: stars |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabir, S.; Leigh, L.; Helder, D. Vicarious Methodologies to Assess and Improve the Quality of the Optical Remote Sensing Images: A Critical Review. Remote Sens. 2020, 12, 4029. https://doi.org/10.3390/rs12244029
Kabir S, Leigh L, Helder D. Vicarious Methodologies to Assess and Improve the Quality of the Optical Remote Sensing Images: A Critical Review. Remote Sensing. 2020; 12(24):4029. https://doi.org/10.3390/rs12244029
Chicago/Turabian StyleKabir, Sakib, Larry Leigh, and Dennis Helder. 2020. "Vicarious Methodologies to Assess and Improve the Quality of the Optical Remote Sensing Images: A Critical Review" Remote Sensing 12, no. 24: 4029. https://doi.org/10.3390/rs12244029
APA StyleKabir, S., Leigh, L., & Helder, D. (2020). Vicarious Methodologies to Assess and Improve the Quality of the Optical Remote Sensing Images: A Critical Review. Remote Sensing, 12(24), 4029. https://doi.org/10.3390/rs12244029