High-Resolution Reconstruction of the Maximum Snow Water Equivalent Based on Remote Sensing Data in a Mountainous Area
Abstract
:1. Introduction
2. Data
2.1. Study Area
2.2. Remote Sensing Data
2.3. Air Temperature Data
2.4. Radiation Data
3. Methodology
3.1. The SWE Reconstruction Model
3.2. The Restricted Degree-Day Model
3.3. Snow Cover
3.3.1. Snow Detection
3.3.2. Cloud Detection and Interpolation
4. Results
4.1. Snow Cover Characteristics in a Mountainous Area
4.1.1. Temporal Variation
4.1.2. Spatial Variation
4.2. The Reconstructed SWE
4.2.1. Temporal Variation
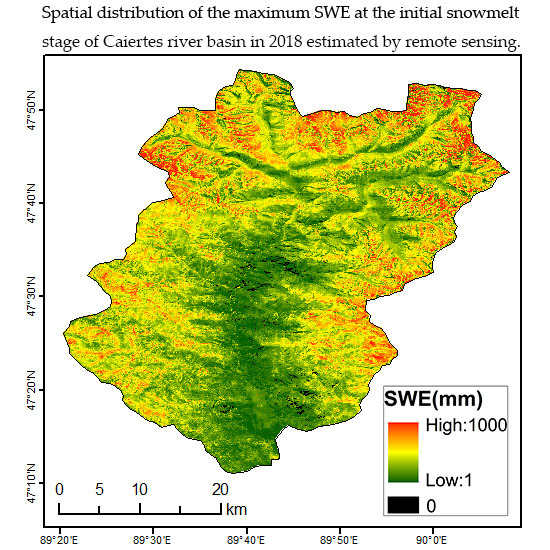
4.2.2. Spatial Variation
5. Discussion
5.1. Snow Cover of Sentinel-2/Landsat and MODIS
5.2. Air Temperature
5.3. Solar Radiation
5.4. Error Analysis
6. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303. [Google Scholar] [CrossRef] [PubMed]
- Bair, E.H.; Rittger, K.; Davis, R.E.; Painter, T.H.; Dozier, J. Validating reconstruction of snow water equivalent in California's Sierra Nevada using measurements from the NASAAirborne Snow Observatory. Water Resour. Res. 2016, 52, 8437–8460. [Google Scholar] [CrossRef]
- Shen, Y.P.; Su, H.C.; Wang, G.Y.; Mao, W.M.; Wang, D.S.; Han, P.; Wang, N.L.; Li, Z.Q. The responses of glaciers and snow cover to climate change in Xinjiang (Ⅰ): Hydrological effect. J. Glaciol. Geocryol. 2013, 3, 513–527. [Google Scholar]
- Pan, J.M.; Jiang, L.M.; Zhang, L.X. Snowmelt estimation of Iii River basin based on physically-based snow process model. In Symposium on Application of Space Information Technology in Water Conservancy Field by China Water Conservancy Society; MDPI: Beijing, China, 2010. [Google Scholar]
- Shen, Y.P.; Su, H.C.; Wang, G.Y.; Mao, W.M.; Wang, D.S.; Han, P.; Wang, N.L.; Li, Z.Q. The responses of glaciers and snow cover to climate change in Xinjiang (Ⅱ): Hazards Effects. J. Glaciol. Geocryol. 2013, 35, 1355–1370. [Google Scholar]
- Zhao, Q.D.; Liu, Z.H.; Fang, S.F.; Lu, Z.; Wang, Y.F.; Li, M. Improved Snowmelt Model Based on EOS/MODIS Remote Sensing Data. J. Arid Land 2007, 30, 915–920. [Google Scholar]
- Zhang, P.; Wang, J.; Liu, Y.; Li, Y. Application of SRM to Flood Forecast and Forwarning of Manasi River Basin in Spring. Remote Sens. Technol. Appl. 2009, 24, 456–461. [Google Scholar]
- Abudu, S.; Cui, C.; King, J.P.; Abudukadeer, K. Comparison of performance of statistical models in forecasting monthly streamflow of Kizil River, China. Water Sci. Eng. 2010, 3, 269–281. [Google Scholar]
- Shi, J.C.; Xiong, C.; Jiang, L.M. Review of snow water equivalent microwave remote sensing. Sci. China Ser. D Earth Sci. 2016, 59, 731–745. [Google Scholar] [CrossRef]
- Dozier, J.; Bair, E.H.; Davis, R.E. Estimating the spatial distribution of snow water equivalent in the world’s mountains. WIREs Water 2016, 3, 461–474. [Google Scholar] [CrossRef]
- Rice, R.; Bales, R.C.; Painter, T.H.; Dozier, J. Snow water equivalent along elevation gradients in the Merced and Tuolumne River basins of the Sierra Nevada. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Rittger, K.; Bair, E.H.; Kahl, A.; Dozier, J. Spatial estimates of snow water equivalent from reconstruction. Adv. Water Resour. 2016, 94, 345–363. [Google Scholar] [CrossRef] [Green Version]
- Fassnacht, S.R.; Dressler, K.A.; Bales, R.C. Snow water equivalent interpolation for the Colorado River Basin from snow telemetry (SNOTEL) data. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef] [Green Version]
- Mätzler, C. Applications of the interaction of microwaves with the natural snow cover. Remote Sens. Rev. 1987, 2, 259–387. [Google Scholar] [CrossRef]
- Chang, A.; Foster, J.L.; Hall, D.K. Nimbus-7 SMMR derived global snow cover parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Kurvonen, L.; Hallikainen, M. Influence of land-cover category on brightness temperature of snow. IEEE Trans. Geosci. Remote 1997, 35, 367–377. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C.; Weise, T. Radiometric and structural measurements of snow samples. Radio Sci. 1998, 33, 273–389. [Google Scholar] [CrossRef]
- Sun, Z.W.; Shi, J.C.; Jiang, L.M.; Yang, H.; Zhang, L.X. Development of snow depth and snow water equivalent algorithm in Western China using passive microwave remote sensing data. Adv. Earth Sci. 2006, 21, 1363–1369. [Google Scholar]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.M.; Wang, P.; Zhang, L.X.; Yang, H.; Yang, J.T. Improvement of snow depth retrieval for FY3B-MWRI in China. Sci. China Ser. D Earth Sci. 2014, 57, 1278–1292. [Google Scholar] [CrossRef]
- Clow, D.W.; Nanus, L.; Verdin, K.L.; Schmidt, J. Evaluation of SNODAS snow depth and snow water equivalent estimates for the Colorado Rocky Mountains, USA. Hydrol. Process. 2012, 26, 2583–2591. [Google Scholar] [CrossRef]
- National Operational Hydrologic Remote Sensing Center Snow Data Assimilation System (SNODAS) Products at NSIDC: National Snow and Ice Data Center. Available online: https://nsidc.org/sites/nsidc.org/files/files/nsidc_special_report_11.pdf (accessed on 15 January 2020).
- Martinec, J.; Rango, A. Areal distribution of snow water equivalent evaluated by snow cover monitoring. Water Resour. Res. 1981, 17, 1480–1488. [Google Scholar] [CrossRef]
- Molotch, N.P.; Bales, R.C. Scaling snow observations from the point to the grid element: Implications for observation network design. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Lettenmaier, D.P.; Alsdorf, D.; Dozier, J.; Huffman, G.J.; Pan, M.; Wood, E.F. Inroads of remote sensing into hydrologic science during the WRR era. Water Resour. Res. 2015, 51, 7309–7342. [Google Scholar] [CrossRef]
- Bair, E.H.; Abreu Calfa, A.A.; Rittger, K.; Dozier, J. Using machine learning for real-time estimates of snow water equivalent in the watersheds of Afghanistan. Cryosphere 2018, 12, 1579–1594. [Google Scholar] [CrossRef] [Green Version]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library. Open Source Geospatial Foundation. Available online: https://gdal.org (accessed on 17 January 2020).
- Zhang, Y.; Enomoto, H.; Ohata, T.; Kitabata, H.; Kadota, T.; Hirabayashi, Y. Glacier mass balance and its potential impacts in the Altai Mountains over the period 1990–2011. J. Hydrol. 2017, 553, 662–677. [Google Scholar] [CrossRef]
- Panagiotopoulos, F.; Shahgedanova, M.; Hannachi, A.; Stephenson, D.B. Observed trends and teleconnections of the Siberian high: A recently declining center of action. J. Climat. 2005, 18, 1411–1422. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.J.; Liu, S.Y.; Guo, W.Q.; Huai, B.J.; Sun, M.P.; Xu, J.L. Glacier Change of Altay Mountain in China from 1960 to 2009—Based on the Second Glacier Inventory of China. Nat. Resour. 2012, 27, 1734–1745. [Google Scholar]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef] [Green Version]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Hollstein, A.; Segl, K.; Guanter, L.; Brell, M.; Enesco, M. Ready-to-use methods for the detection of clouds, cirrus, snow, shadow, water and clear sky pixels in Sentinel-2 MSI images. Remote Sens.-Basel. 2016, 8, 666. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Martinec, J.; Rango, A.; Major, E. The Snowmelt-Runoff Model (SRM) User’s Manual. 1983. Available online: https://ntrs.nasa.gov/search.jsp?R=19830015389 (accessed on 15 January 2020).
- Winstral, A.; Marks, D.; Gurney, R. Assessing the sensitivities of a distributed snow model to forcing data resolution. J. Hydrometeorol. 2014, 15, 1366–1383. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, T.; Shi, J.; Zhou, W. A Lut-Based Method to Estimate Clear-Sky Instantaneous Land Surface Shortwave Downward Radiation and its Direct Component from Modis Data. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, IEEE, Yokohama, Japan, 28 July–2 August 2019; pp. 1861–1864. [Google Scholar] [CrossRef]
- Wang, T.; Yan, G.; Mu, X.; Jiao, Z.; Chen, L.; Chu, Q. Toward operational shortwave radiation modeling and retrieval over rugged terrain. Remote Sens. Environ. 2018, 205, 419–433. [Google Scholar] [CrossRef]
- Molotch, N.P.; Margulis, S.A. Estimating the distribution of snow water equivalent using remotely sensed snow cover data and a spatially distributed snowmelt model: A multi-resolution, multi-sensor comparison. Adv. Water Resour. 2008, 31, 1503–1514. [Google Scholar] [CrossRef]
- Molotch, N.P. Reconstructing snow water equivalent in the Rio Grande headwaters using remotely sensed snow cover data and a spatially distributed snowmelt model. Hydrol. Process 2009, 23, 1076–1089. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. REVISITING THE DEGREE-DAY METHOD FOR SNOWMELT COMPUTATIONS 1. J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Brubaker, K.; Rango, A.; Kustas, W. Incorporating radiation inputs into the snowmelt runoff model. Hydrol. Process. 1996, 10, 1329–1343. [Google Scholar] [CrossRef]
- Dozier, J. Spectral signature of alpine snow cover from the Landsat Thematic Mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Chokmani, K.; Dever, K.; Bernier, M.; Gauthier, Y.; Paquet, L. Adaptation of the SNOWMAP algorithm for snow mapping over eastern Canada using Landsat-TM imagery. Hydrol. Sci. J. 2010, 55, 649–660. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of subpixel snow covered area, grain size, and albedo from MODIS. Remote Sens. Environ. 2009, 113, 868–879. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 1995, 54, 127–140. [Google Scholar] [CrossRef]
- Negi, H.S.; Kulkarni, A.V.; Semwal, B.S. Estimation of snow cover distribution in Beas basin, Indian Himalaya using satellite data and ground measurements. J. Earth Syst. Sci. 2009, 118, 525. [Google Scholar] [CrossRef]
- Kulkarni, A.V.; Srinivasulu, J.; Manjul, S.S.; Mathur, P. Field based spectral reflectance studies to develop NDSI method for snow cover monitoring. J. Indian Soc. Remote 2002, 30, 73–80. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Coluzzi, R.; Imbrenda, V.; Lanfredi, M.; Simoniello, T. A first assessment of the Sentinel-2 Level 1-C cloud mask product to support informed surface analyses. Remote Sens. Environ. 2018, 217, 426–443. [Google Scholar] [CrossRef]
- Dozier, J.; Painter, T.H.; Rittger, K.; Frew, J.E. Time–space continuity of daily maps of fractional snow cover and albedo from MODIS. Adv. Water Resour. 2008, 31, 1515–1526. [Google Scholar] [CrossRef]
- Grünewald, T.; Bühler, Y.; Lehning, M. Elevation dependency of mountain snow depth. Cryosphere 2014, 8, 2381–2394. [Google Scholar]
- Strasser, U.; Bernhardt, M.; Weber, M.; Liston, G.E.; Mauser, W. Is snow sublimation important in the alpine water balance? Cryosphere 2008, 2, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Liang, T.; Zhang, X.; Guo, Z. Validation of MODIS snow cover products using Landsat and ground measurements during the 2001–2005 snow seasons over northern Xinjiang, China. Int. J. Remote Sens. 2011, 32, 133–152. [Google Scholar] [CrossRef]
- Marks, D.; Dozier, J. Climate and energy exchange at the snow surface in the alpine region of the Sierra Nevada: 2. Snow cover energy balance. Water Resour. Res. 1992, 28, 3043–3054. [Google Scholar] [CrossRef]
- Mahat, V.; Tarboton, D.G. Canopy radiation transmission for an energy balance snowmelt model. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Raleigh, M.S.; Lundquist, J.D. Comparing and combining SWE estimates from the SNOW-17 model using PRISM and SWE reconstruction. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]













| Sensor | Channel | Band Number | Wavelength Range (μm) | Spatial Resolution (m) | Temporal Resolution (day) |
|---|---|---|---|---|---|
| Landsat8 OLI | Blue | 2 | 0.45–0.51 | 30 | 16 |
| Green | 3 | 0.53–0.59 | 30 | ||
| NIR 1 | 5 | 0.85–0.88 | 30 | ||
| SWIR1 2 | 6 | 1.57–1.65 | 30 | ||
| PAN | 8 | 0.50–0.68 | 15 | ||
| SWIR-Cirrus | 9 | 1.36–1.38 | 30 | ||
| Sentinel-2 MSI | Blue | 2 | 0.458–0.523 | 10 | 5 |
| Green | 3 | 0.543–0.578 | 10 | ||
| Red Range1 | 5 | 0.698–0.713 | 20 | ||
| Red Range2 | 6 | 0.733–0.748 | 20 | ||
| NIR Narrow1 | 7 | 0.765–0.785 | 20 | ||
| NIR | 8 | 0.785–0.900 | 10 | ||
| Cirrus | 8a | 0.855–0.875 | 20 | ||
| Water Vapour | 9 | 0.930–0.950 | 60 | ||
| SWIR-Cirrus | 10 | 1.365–1.385 | 60 | ||
| SWIR1 | 11 | 1.565–1.655 | 20 | ||
| SWIR2 | 12 | 2.100–2.280 | 20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Xiong, C.; Pan, J.; Wang, T.; Shi, J.; Wang, N. High-Resolution Reconstruction of the Maximum Snow Water Equivalent Based on Remote Sensing Data in a Mountainous Area. Remote Sens. 2020, 12, 460. https://doi.org/10.3390/rs12030460
Liu M, Xiong C, Pan J, Wang T, Shi J, Wang N. High-Resolution Reconstruction of the Maximum Snow Water Equivalent Based on Remote Sensing Data in a Mountainous Area. Remote Sensing. 2020; 12(3):460. https://doi.org/10.3390/rs12030460
Chicago/Turabian StyleLiu, Mingyu, Chuan Xiong, Jinmei Pan, Tianxing Wang, Jiancheng Shi, and Ninglian Wang. 2020. "High-Resolution Reconstruction of the Maximum Snow Water Equivalent Based on Remote Sensing Data in a Mountainous Area" Remote Sensing 12, no. 3: 460. https://doi.org/10.3390/rs12030460
APA StyleLiu, M., Xiong, C., Pan, J., Wang, T., Shi, J., & Wang, N. (2020). High-Resolution Reconstruction of the Maximum Snow Water Equivalent Based on Remote Sensing Data in a Mountainous Area. Remote Sensing, 12(3), 460. https://doi.org/10.3390/rs12030460