Characterizing and Mitigating Sensor Generated Spatial Correlations in Airborne Hyperspectral Imaging Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Airborne HSI Data
2.2. Deriving the Theoretical Point Spread Function for each CASI Pixel
2.3. Simulated HSI Data
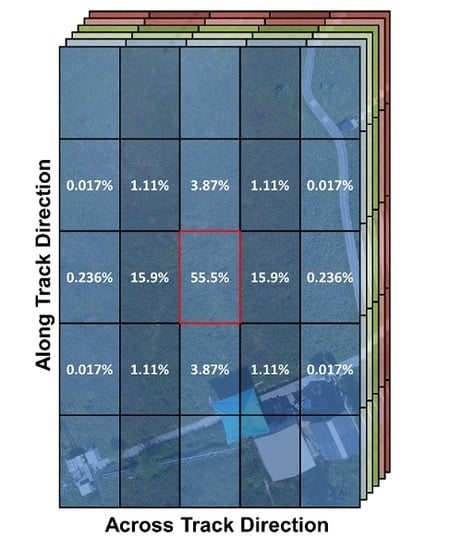
2.4. Visualizing and Quantifying Spatial Correlations
2.5. Mitigating Sensor Generated Spatial Correlations Using the PSFnet
2.6. Algorithm Application to Simulated HSI Data
2.7. Algorithm Application to Real-World HSI Data
3. Results
3.1. Theoretical Point Spread Function for Each CASI Pixel
3.2. Simulated HSI Data
3.3. Algorithm Application to Simulated HSI Data
3.4. Algorithm Application to Real-World HSI Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M. Imaging spectroscopy and the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ. 1998, 65, 227–248. [Google Scholar] [CrossRef]
- Cocks, T.; Jenssen, R.; Stewart, A.; Wilson, I.; Shields, T. The HyMapTM airborne hyperspectral sensor: The system, calibration and performance. In Proceedings of the 1st EARSeL Workshop on Imaging Spectroscopy, Zurich, Switzerland, 6–8 October 1998; pp. 37–42. [Google Scholar]
- Babey, S.; Anger, C. A compact airborne spectrographic imager (CASI). In Proceedings of the IGARSS ’89 Quantitative Remote Sensing: An Economic Tool for the Nineties, New York, NY, USA, 10–14 July 1989; Volume 2, pp. 1028–1031. [Google Scholar]
- Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, S.L. Hyperion, a space-based imaging spectrometer. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1160–1173. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Eismann, M.T. 1.1 Hyperspectral Remote Sensing. In Hyperspectral Remote Sensing; SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd Jr, J.H.; Richtsmeier, S.C.; Pukall, B. MODTRAN4 radiative transfer modeling for atmospheric correction. In Proceedings of the Optical Spectroscopic Techniques and instrumentation for atmospheric and space research III, Denver, CO, USA, 18–23 July 1999; pp. 348–353. [Google Scholar]
- Cloutis, E.A. Review article hyperspectral geological remote sensing: Evaluation of analytical techniques. Int. J. Remote Sens. 1996, 17, 2215–2242. [Google Scholar] [CrossRef]
- Murphy, R.J.; Monteiro, S.T.; Schneider, S. Evaluating classification techniques for mapping vertical geology using field-based hyperspectral sensors. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3066–3080. [Google Scholar] [CrossRef]
- van der Meer, F.D.; van der Werff, H.M.A.; van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; Smeth, J.B.d.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- Yao, H.; Tang, L.; Tian, L.; Brown, R.; Bhatnagar, D.; Cleveland, T. Using hyperspectral data in precision farming applications. Hyperspectral Remote Sens. Veg. 2011, 1, 591–607. [Google Scholar]
- Dale, L.M.; Thewis, A.; Boudry, C.; Rotar, I.; Dardenne, P.; Baeten, V.; Pierna, J.A.F. Hyperspectral imaging applications in agriculture and agro-food product quality and safety control: A review. Appl. Spectrosc. Rev. 2013, 48, 142–159. [Google Scholar] [CrossRef]
- Migdall, S.; Klug, P.; Denis, A.; Bach, H. The additional value of hyperspectral data for smart farming. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), 2012 IEEE International, Munich, Germany, 22–27 July 2012; pp. 7329–7332. [Google Scholar]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm. Remote Sens. 2010, 65, 581–590. [Google Scholar] [CrossRef]
- Peng, G.; Ruiliang, P.; Biging, G.S.; Larrieu, M.R. Estimation of forest leaf area index using vegetation indices derived from hyperion hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.-L.; Martin, M.E.; Plourde, L.; Ollinger, S.V. Analysis of hyperspectral data for estimation of temperate forest canopy nitrogen concentration: Comparison between an airborne (AVIRIS) and a spaceborne (Hyperion) sensor. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1332–1337. [Google Scholar] [CrossRef]
- Kruse, F.A.; Richardson, L.L.; Ambrosia, V.G. Techniques developed for geologic analysis of hyperspectral data applied to near-shore hyperspectral ocean data. In Proceedings of the Fourth International Conference on Remote Sensing for Marine and Coastal Environments, Orlando, FL, USA, 17–19 March 1997; p. 19. [Google Scholar]
- Chang, G.; Mahoney, K.; Briggs-Whitmire, A.; Kohler, D.; Mobley, C.; Lewis, M.; Moline, M.; Boss, E.; Kim, M.; Philpot, W. The New Age of Hyperspectral Oceanography. Oceanography 2004, 17, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Ryan, J.P.; Davis, C.O.; Tufillaro, N.B.; Kudela, R.M.; Gao, B.-C. Application of the hyperspectral imager for the coastal ocean to phytoplankton ecology studies in Monterey Bay, CA, USA. Remote Sens. 2014, 6, 1007–1025. [Google Scholar] [CrossRef] [Green Version]
- Kalacska, M.; Bell, L. Remote sensing as a tool for the detection of clandestine mass graves. Can. Soc. Forensic Sci. J. 2006, 39, 1–13. [Google Scholar] [CrossRef]
- Kalacska, M.E.; Bell, L.S.; Arturo Sanchez-Azofeifa, G.; Caelli, T. The application of remote sensing for detecting mass graves: An experimental animal case study from Costa Rica. J. Forensic Sci. 2009, 54, 159–166. [Google Scholar] [CrossRef]
- Leblanc, G.; Kalacska, M.; Soffer, R. Detection of single graves by airborne hyperspectral imaging. Forensic Sci. Int. 2014, 245, 17–23. [Google Scholar] [CrossRef]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.; Kalacska, M.; Soffer, R.; Moore, T.; Roulet, N.; Juutinen, S.; Ifimov, G.; Leblanc, G.; Inamdar, D. Airborne Hyperspectral Evaluation of Maximum Gross Photosynthesis, Gravimetric Water Content, and CO2 Uptake Efficiency of the Mer Bleue Ombrotrophic Peatland. Remote Sens. 2018, 10, 565. [Google Scholar] [CrossRef] [Green Version]
- Kalacska, M.; Arroyo-Mora, J.; Soffer, R.; Roulet, N.; Moore, T.; Humphreys, E.; Leblanc, G.; Lucanus, O.; Inamdar, D. Estimating peatland water table depth and net ecosystem exchange: A comparison between satellite and airborne imagery. Remote Sens. 2018, 10, 687. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Townshend, J.R.; Liang, S.; Kalluri, S.N.; DeFries, R.S. Impact of sensor’s point spread function on land cover characterization: Assessment and deconvolution. Remote Sens. Environ. 2002, 80, 203–212. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. 3.4. Spatial Response. In Remote Sensing: Models and Methods for Image Processing; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Zhang, Z.; Moore, J.C. Chapter 4—Remote Sensing. In Mathematical and Physical Fundamentals of Climate Change; Zhang, Z., Moore, J.C., Eds.; Elsevier: Boston, MA, USA, 2015; pp. 111–124. [Google Scholar] [CrossRef]
- Schowengerdt, R.A.; Antos, R.L.; Slater, P.N. Measurement Of The Earth Resources Technology Satellite (Erts-1) Multi-Spectral Scanner OTF From Operational Imagery; SPIE: Bellingham, WA, USA, 1974; Volume 46. [Google Scholar]
- Rauchmiller, R.F.; Schowengerdt, R.A. Measurement Of The Landsat Thematic Mapper Modulation Transfer Function Using An Array Of Point Sources. Opt. Eng. 1988, 27, 334–343. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Velmurugan, R.; Rameshan, R. Chapter 2 Mathematical Background. In Blind Image Deconvolution: Methods and Convergence; Springer International Publishing: Madrid, Spain, 2014. [Google Scholar]
- Hu, W.; Xue, J.; Zheng, N. PSF estimation via gradient domain correlation. IEEE Trans. Image Process. 2012, 21, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Markham, B.L.; Arvidson, T.; Barsi, J.A.; Choate, M.; Kaita, E.; Levy, R.; Lubke, M.; Masek, J.G. 1.03—Landsat Program. In Comprehensive Remote Sensing; Liang, S., Ed.; Elsevier: Oxford, UK, 2018; pp. 27–90. [Google Scholar] [CrossRef]
- Markham, B.L. The Landsat sensors’ spatial responses. IEEE Trans. Geosci. Remote Sens. 1985, 6, 864–875. [Google Scholar] [CrossRef]
- Radoux, J.; Chomé, G.; Jacques, D.C.; Waldner, F.; Bellemans, N.; Matton, N.; Lamarche, C.; d’Andrimont, R.; Defourny, P. Sentinel-2’s potential for sub-pixel landscape feature detection. Remote Sens. 2016, 8, 488. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Shi, W.; Atkinson, P.M. Enhancing spectral unmixing by considering the point spread function effect. Spat. Stat. 2018, 28, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Aiazzi, B.; Selva, M.; Arienzo, A.; Baronti, S. Influence of the System MTF on the On-Board Lossless Compression of Hyperspectral Raw Data. Remote Sens. 2019, 11, 791. [Google Scholar] [CrossRef] [Green Version]
- Bergen, K.M.; Brown, D.G.; Rutherford, J.F.; Gustafson, E.J. Change detection with heterogeneous data using ecoregional stratification, statistical summaries and a land allocation algorithm. Remote Sens. Environ. 2005, 97, 434–446. [Google Scholar] [CrossRef]
- Simms, D.M.; Waine, T.W.; Taylor, J.C.; Juniper, G.R. The application of time-series MODIS NDVI profiles for the acquisition of crop information across Afghanistan. Int. J. Remote Sens. 2014, 35, 6234–6254. [Google Scholar] [CrossRef] [Green Version]
- Tarrant, P.; Amacher, J.; Neuer, S. Assessing the potential of Medium-Resolution Imaging Spectrometer (MERIS) and Moderate-Resolution Imaging Spectroradiometer (MODIS) data for monitoring total suspended matter in small and intermediate sized lakes and reservoirs. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Heiskanen, J. Tree cover and height estimation in the Fennoscandian tundra–taiga transition zone using multiangular MISR data. Remote Sens. Environ. 2006, 103, 97–114. [Google Scholar] [CrossRef]
- Torres-Rua, A.; Ticlavilca, A.; Bachour, R.; McKee, M. Estimation of surface soil moisture in irrigated lands by assimilation of landsat vegetation indices, surface energy balance products, and relevance vector machines. Water 2016, 8, 167. [Google Scholar] [CrossRef] [Green Version]
- Schlapfer, D.; Nieke, J.; Itten, K.I. Spatial PSF nonuniformity effects in airborne pushbroom imaging spectrometry data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 458–468. [Google Scholar] [CrossRef]
- Fang, H.; Luo, C.; Zhou, G.; Wang, X. Hyperspectral image deconvolution with a spectral-spatial total variation regularization. Can. J. Remote Sens. 2017, 43, 384–395. [Google Scholar] [CrossRef]
- Henrot, S.; Soussen, C.; Brie, D. Fast positive deconvolution of hyperspectral images. IEEE Trans. Image Process. 2013, 22, 828–833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jackett, C.; Turner, P.; Lovell, J.; Williams, R. Deconvolution of MODIS imagery using multiscale maximum entropy. Remote Sens. Lett. 2011, 2, 179–187. [Google Scholar] [CrossRef]
- Soffer, R.J.; Ifimov, G.; Arroyo-Mora, J.P.; Kalacska, M. Validation of Airborne Hyperspectral Imagery from Laboratory Panel Characterization to Image Quality Assessment: Implications for an Arctic Peatland Surrogate Simulation Site. Can. J. Remote Sens. 2019, 1–33. [Google Scholar] [CrossRef]
- Lafleur, P.M.; Roulet, N.T.; Bubier, J.; Frolking, S.; Moore, T.R. Interannual variability in the peatland-atmosphere carbon dioxide exchange at an ombrotrophic bog. Glob. Biogeochem. Cycles 2003, 17, 13. [Google Scholar] [CrossRef] [Green Version]
- Eppinga, M.B.; Rietkerk, M.; Borren, W.; Lapshina, E.D.; Bleuten, W.; Wassen, M.J. Regular Surface Patterning of Peatlands: Confronting Theory with Field Data. Ecosystems 2008, 11, 520–536. [Google Scholar] [CrossRef] [Green Version]
- Lafleur, P.M.; Hember, R.A.; Admiral, S.W.; Roulet, N.T. Annual and seasonal variability in evapotranspiration and water table at a shrub-covered bog in southern Ontario, Canada. Hydrol. Process. 2005, 19, 3533–3550. [Google Scholar] [CrossRef]
- Wilson, P. The Relationship among Micro-Topographical Variation, Water Table Depth and Biogeochemistry in an Ombrotrophic Bog; McGill University Libraries: Montreal, QC, Canada, 2012. [Google Scholar]
- Malhotra, A.; Roulet, N.T.; Wilson, P.; Giroux-Bougard, X.; Harris, L.I. Ecohydrological feedbacks in peatlands: An empirical test of the relationship among vegetation, microtopography and water table. Ecohydrology 2016, 9, 1346–1357. [Google Scholar] [CrossRef]
- Belyea, L.R.; Baird, A.J. Beyond “The Limits To Peat Bog Growth”: Cross-Scale Feedback In Peatland Development. Ecol. Monogr. 2006, 76, 299–322. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.P.; Kalacska, M.; Soffer, R.; Ifimov, G.; Leblanc, G.; Schaaf, E.S.; Lucanus, O. Evaluation of phenospectral dynamics with Sentinel-2A using a bottom-up approach in a northern ombrotrophic peatland. Remote Sens. Environ. 2018, 216, 544–560. [Google Scholar] [CrossRef]
- Puttonen, E.; Suomalainen, J.; Hakala, T.; Peltoniemi, J. Measurement of Reflectance Properties of Asphalt Surfaces and Their Usability as Reference Targets for Aerial Photos. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2330–2339. [Google Scholar] [CrossRef]
- Inamdar, D.; Leblanc, G.; Soffer, R.J.; Kalacska, M. The Correlation Coefficient as a Simple Tool for the Localization of Errors in Spectroscopic Imaging Data. Remote Sens. 2018, 10, 231. [Google Scholar] [CrossRef] [Green Version]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Townshend, J.; Huang, C.; Kalluri, S.; Defries, R.; Liang, S.; Yang, K. Beware of per-pixel characterization of land cover. Int. J. Remote Sens. 2000, 21, 839–843. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Landgrebe, D.A. Analyzing high-dimensional multispectral data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 792–800. [Google Scholar] [CrossRef] [Green Version]
- Arroyo-Mora, J.P.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.S.; Ifimov, G.; Elmer, K. Implementation of a UAV–Hyperspectral Pushbroom Imager for Ecological Monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- Warren, M.A.; Taylor, B.H.; Grant, M.G.; Shutler, J.D. Data processing of remotely sensed airborne hyperspectral data using the Airborne Processing Library (APL): Geocorrection algorithm descriptions and spatial accuracy assessment. Comput. Geosci. 2014, 64, 24–34. [Google Scholar] [CrossRef] [Green Version]
















| Parameter | Mer Bleue Peatland | Macdonald-Cartier International Airport |
|---|---|---|
| Time (hh:mm:ss GMT) | 16:31:15 | 17:42:05 |
| Date (dd/mm/yyyy) | 24/06/2016 | 24/06/2016 |
| Latitude of Flight Line Centre (DD) | 45.399499 | 45.323259 |
| Longitude of Flight Line Centre (DD) | −75.514790 | −75.660129 |
| Nominal Heading (°TN) | 338.0 | 309.5 |
| Nominal Altitude (m) | 1142 | 1118 |
| Nominal Speed (m/s) | 41.5 | 41.6 |
| Integration Time (ms) | 48 | 48 |
| Frame Time (ms) | 48 | 48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inamdar, D.; Kalacska, M.; Leblanc, G.; Arroyo-Mora, J.P. Characterizing and Mitigating Sensor Generated Spatial Correlations in Airborne Hyperspectral Imaging Data. Remote Sens. 2020, 12, 641. https://doi.org/10.3390/rs12040641
Inamdar D, Kalacska M, Leblanc G, Arroyo-Mora JP. Characterizing and Mitigating Sensor Generated Spatial Correlations in Airborne Hyperspectral Imaging Data. Remote Sensing. 2020; 12(4):641. https://doi.org/10.3390/rs12040641
Chicago/Turabian StyleInamdar, Deep, Margaret Kalacska, George Leblanc, and J. Pablo Arroyo-Mora. 2020. "Characterizing and Mitigating Sensor Generated Spatial Correlations in Airborne Hyperspectral Imaging Data" Remote Sensing 12, no. 4: 641. https://doi.org/10.3390/rs12040641
APA StyleInamdar, D., Kalacska, M., Leblanc, G., & Arroyo-Mora, J. P. (2020). Characterizing and Mitigating Sensor Generated Spatial Correlations in Airborne Hyperspectral Imaging Data. Remote Sensing, 12(4), 641. https://doi.org/10.3390/rs12040641