Scatter Matrix Based Domain Adaptation for Bi-Temporal Polarimetric SAR Images
Abstract
:1. Introduction
2. Methods
2.1. Relevant Works
2.1.1. Transfer Component Analysis
- Shorten the distribution distance between and as much as possible
- Preserve the valuable information of original data and after the transformation
- Reduce the empirical error on the SD labeled data as much as possible
- Preserve the local structure information of original data and after the transformation
2.1.2. Maximum Independence Domain Adaptation
2.2. PolSAR Data Description
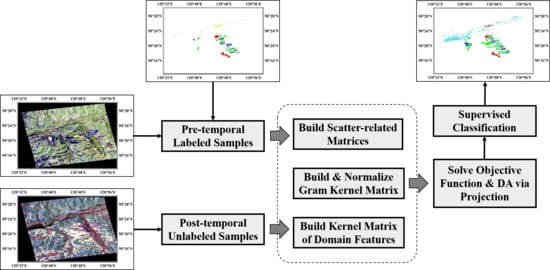
2.3. Scatter Matrix Based Domain Adaptation
2.3.1. Supervised Information Preservation
2.3.2. Unsupervised Information Preservation
2.3.3. Domain Influence Reduction
2.4. Wishart-Based Radial Basis Function
| Algorithm 1. SMbDA |
| Input: SD and TD sample sets ,, and SD label set |
| Output: projection matrix |
| Step 1. Define domain feature of each sample based on (1) and form domain feature matrix |
| Step 2. Construct Gram kernel matrix based on (6) (Wishart-based RBF is recommended) |
| Step 3. Normalize as |
| Step 4. Construct two scatter-related matrices and based on (19) and (20) |
| Step 5. Calculate the kernel matrix of domain features, |
| Step 6. Eigen decompose the matrix |
| Step 7. Select the leading eigenvectors to construct the projection matrix |
2.5. Relationship with Other Methods
- If the SD and TD data are regarded as a whole without considering inter-domain discrepancy, the Gram kernel matrix degrades into traditional kernel matrix, and accordingly the unsupervised information preservation term degrades into the objective function of standard PCA in kernel spaces. Then if we set , SMbDA is the same as kernel PCA.
- If we only pay attention to SD samples, SMbDA is further simplified down to a kernel-based combination of MMC and PCA, which can be seen as a semi-supervised dimensionality reduction algorithm. We use two core matrices and to capture scatter information and preserve category separability. Originally, the two matrices were used in LDA and kernel LDA. In this paper, they are generalized and reused for dual-domain kernel matrix. In source domain, our SMbDA is similar to the idea in [51], in which a combination of local LDA and PCA was discussed.
- As the inter- and intra-category scatter matrices have been reformed in [49], the proposed algorithm has an implicit relationship with the graph embedding framework. From this perspective, the term can be regarded as a special Laplacian matrix.
- SMbDA, TCA and MIDA have some points in common. All of the three algorithms use the covariance matrix of data to keep unsupervised information, and try to reduce the negative cross-domain influence. However, TCA, MIDA and their semi-supervised extensions primarily consider unsupervised information. On the contrary, SMbDA primarily makes full use of label information to keep category separability, which makes it more benefit for classification in theory. Besides, SMbDA avoids inversion operation when solving projection matrix, and thus is more efficient than TCA and SSTCA.
3. Materials and Results
3.1. Experimental Datasets and Parameter Settings
3.2. Experiments on UAVSAR Dataset
3.3. Experiments on Radarsat-2 Dataset
4. Discussion
- No matter in which task, the OA and Kappa values are generally upgraded after DA processing. It is proved that DA is of significant help for these classification tasks, especially the three tasks, Domain B -> Domain A, Domain A -> Domain C and Domain B -> Domain C.
- Compared with TCA and MIDA, SSTCA and SMIDA are more conducive to improving interpretation performances, as both of them take label information into account. Even in the worst case, the two can be respectively equivalent to TCA and MIDA.
- In all of the tasks, our proposed SMbDA caused no negative transfer effect, and has achieved better performances than TCA, SSCTA, MIDA and SMIDA in half of the tasks. In the other half, the OA and Kappa values of SMbDA are basically close to the best ones.
- WSMbDA can further improve the performances of SMbDA in most cases, and has obtained the best results in general, which verifies the superiority of Wishart-based RBF. The well-designed DA model SMbDA, coupled with the suitable kernel mapping function, is able to achieve the average OA value of more than 80% and the average Kappa value of more than 0.75.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, W.; Li, P.; Yang, J.; Zhao, L.; Li, M. Polarimetric SAR Image Classification Using a Wishart Test Statistic and a Wishart Dissimilarity Measure. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote. Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Liu, F.; Jiao, L.; Hou, B.; Yang, S. POL-SAR Image Classification Based on Wishart DBN and Local Spatial Information. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 3292–3308. [Google Scholar] [CrossRef]
- Shang, R.; Wang, G.; Okoth, M.A.; Jiao, L. Complex-Valued Convolutional Autoencoder and Spatial Pixel-Squares Refinement for Polarimetric SAR Image Classification. Remote. Sens. 2019, 11, 522. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Gierull, C.H. A New Application for PolSAR Imagery in the Field of Moving Target Indication/Ship Detection. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 3426–3436. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Sato, M. Urban Damage Level Mapping Based on Scattering Mechanism Investigation Using Fully Polarimetric SAR Data for the 3.11 East Japan Earthquake. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 6919–6929. [Google Scholar] [CrossRef]
- Zhai, W.; Huang, C.; Pei, W. Building Damage Assessment Based on the Fusion of Multiple Texture Features Using a Single Post-Earthquake PolSAR Image. Remote. Sens. 2019, 11, 897. [Google Scholar] [CrossRef] [Green Version]
- Hajnsek, I.; Papathanassiou, K.P.; Jagdhuber, T.; Schon, H. Potential of Estimating Soil Moisture Under Vegetation Cover by Means of PolSAR. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef] [Green Version]
- Tanase, M.A.; Panciera, R.; Lowell, K.; Tian, S.; Hacker, J.M.; Walker, J.P. Airborne multi-temporal L-band polarimetric SAR data for biomass estimation in semi-arid forests. Remote. Sens. Environ. 2014, 145, 93–104. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Xiao, S.-P. Urban Damage Level Mapping Based on Co-Polarization Coherence Pattern Using Multitemporal Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 2657–2667. [Google Scholar] [CrossRef]
- Mascolo, L.; Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Nunziata, F.; Migliaccio, M.; Mazzarella, G. A Complete Procedure for Crop Phenology Estimation with PolSAR Data Based on the Complex Wishart Classifier. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 6505–6515. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Yang, J.; Li, P.; Zhang, L. Seasonal inundation monitoring and vegetation pattern mapping of the Erguna floodplain by means of a RADARSAT-2 fully polarimetric time series. Remote. Sens. Environ. 2014, 152, 426–440. [Google Scholar] [CrossRef]
- Marechal, C.; Pottier, E.; Hubert-Moy, L.; Rapinel, S.; Cécile Marechal, I.E.T. R – UMR CNRS University of Rennes Campus de Beaulieu Bat D av Gal Leclerc F- Rennes Cedex France.; Eric Pottier I.E.T.R – UMR CNRS University of Rennes Campus de Beaulieu Bat D av Gal Leclerc F- Rennes Cedex France.Correspondenceeric.pottieruniv-rennes.freric.pottieruniv-rennes.fr One year wetland survey investigations from quad-pol RADARSAT-2 time-series SAR images. Can. J. Remote. Sens. 2012, 38, 240–252. [Google Scholar]
- Antropov, O.; Rauste, Y.; Häme, T.; Praks, J. Polarimetric ALOS PALSAR Time Series in Mapping Biomass of Boreal Forests. Remote. Sens. 2017, 9, 999. [Google Scholar] [CrossRef] [Green Version]
- Alonso-González, A.; López-Martínez, C.; Salembier, P. PolSAR Time Series Processing with Binary Partition Trees. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 3553–3567. [Google Scholar] [CrossRef] [Green Version]
- Lê, T.T.; Atto, A.M.; Trouvé, E.; Solikhin, A.; Pinel, V. Change detection matrix for multitemporal filtering and change analysis of SAR and PolSAR image time series. ISPRS J. Photogramm. Remote. Sens. 2015, 107, 64–76. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, J.; Lu, Z.; Li, P.; Liu, W.; Yang, L. A Novel Method of Change Detection in Bi-Temporal PolSAR Data Using a Joint-Classification Classifier Based on a Similarity Measure. Remote. Sens. 2017, 9, 846. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Yang, J.; Zhao, J.; Shi, H.; Yang, L. An Unsupervised Change Detection Method Using Time-Series of PolSAR Images from Radarsat-2 and GaoFen-3. Sensors 2018, 18, 559. [Google Scholar]
- Zhou, W.; Troy, A.R.; Grove, M. Object-based Land Cover Classification and Change Analysis in the Baltimore Metropolitan Area Using Multitemporal High Resolution Remote Sensing Data. Sensors 2008, 8, 1613–1636. [Google Scholar] [CrossRef] [Green Version]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Zhang, X. A three-component method for timely detection of land cover changes using polarimetric SAR images. ISPRS J. Photograms. Remote. Sens. 2015, 107, 3–21. [Google Scholar] [CrossRef]
- Kong, J.A.; Swartz, A.A.; Yueh, H.A.; Novak, L.M.; Shin, R.T. Identification of Terrain Cover Using the Optimum Polarimetric Classifier. Journal of Electromagnetic Waves and Applications 1988, 2, 171–194. [Google Scholar]
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote. Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Ferro-Famil, L.; Pottier, E.; Lee, J.-S. Unsupervised classification of multifrequency and fully polarimetric SAR images based on the H/A/Alpha-Wishart classifier. IEEE Trans. Geosci. Remote. Sens. 2001, 39, 2332–2342. [Google Scholar] [CrossRef]
- Lardeux, C.; Frison, P.-L.; Tison, C.; Souyris, J.-C.; Stoll, B.; Fruneau, B.; Rudant, J.-P. Support Vector Machine for Multifrequency SAR Polarimetric Data Classification. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 4143–4152. [Google Scholar] [CrossRef]
- Loosvelt, L.; Peters, J.; Skriver, H.; De Baets, B.; Verhoest, N. Impact of Reducing Polarimetric SAR Input on the Uncertainty of Crop Classifications Based on the Random Forests Algorithm. IEEE Trans. Geosci. Remote. Sens. 2012, 50, 4185–4200. [Google Scholar] [CrossRef]
- Qin, F.; Guo, J.; Sun, W. Object-Oriented Ensemble Classification for Polarimetric SAR Imagery Using Restricted Boltzmann Machines. Remote. Sens. L 2017, 8, 204–213. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Liu, G.; Jiao, L. A Novel Deep Fully Convolutional Network for PolSAR Image Classification. Remote. Sens. 2018, 10, 1984. [Google Scholar] [CrossRef] [Green Version]
- Tsung, F.; Zhang, K.; Cheng, L.; Song, Z. Statistical Transfer Learning: A Review and Some Extensions to Statistical Process Control. Quality Engineering 2018, 30, 115–128. [Google Scholar] [CrossRef]
- Segev, N.; Harel, M.; Mannor, S.; Crammer, K.; El-Yaniv, R. Learn on Source, Refine on Target: A Model Transfer Learning Framework with Random Forests. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1811–1824. [Google Scholar] [CrossRef] [Green Version]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Transactions on Knowledge and Data Engineering 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Argyriou, A.; Evgeniou, T.; Pontil, M. Multi-Task Feature Learning. In Proceedings of the Twenty-First Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007. [Google Scholar]
- Argyriou, A.; Micchelli, C.A.; Pontil, M.; Ying, Y. A Spectral Regularization Framework for Multi-Task Structure Learning. In Proceedings of the Twenty-Second Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–11 December 2008. [Google Scholar]
- Blitzer, J.; McDonald, R.; Pereira, F. Domain adaptation with structural correspondence learning. In Proceedings of the 2006 Conference on Empirical Methods in Natural Language Processing, Sydney, Australia, 22–23 July 2006; p. 120. [Google Scholar]
- Shao, M.; Kit, D.; Fu, Y. Generalized Transfer Subspace Learning Through Low-Rank Constraint. Int. J. Comput. Vis. 2014, 109, 74–93. [Google Scholar] [CrossRef]
- Pan, S.J.; Kwok, J.T.; Yang, Q. Transfer Learning via Dimensionality Reduction. In Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence, Chicago, IL, USA, 13–17 July 2008. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Networks 2011, 22, 199–210. [Google Scholar] [CrossRef] [Green Version]
- Yan, K.; Kou, L.; Kwok, J.T.; Zhang, D. Learning Domain-Invariant Subspace Using Domain Features and Independence Maximization. IEEE Trans. Cybern. 2018, 48, 288–299. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, S. Transfer sparse machine: Matching joint distribution by subspace learning and classifier transduction. In Proceedings of the Eighth International Conference on Digital Image Processing (ICDIP 2016), Chengu, China, 20–22 May 2016; Volume 10033, p. 100335Z. [Google Scholar]
- Zhang, X.; Yu, F.X.; Chang, S.-F.; Wang, S. Deep Transfer Network: Unsupervised Domain Adaptation. arXiv 2015, arXiv:1503.00591. [Google Scholar]
- Huang, J.-T.; Li, J.; Yu, N.; Deng, L.; Gong, Y. Cross-language knowledge transfer using multilingual deep neural network with shared hidden layers. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 7304–7308. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Darrell, T.; Saenko, K. Simultaneous Deep Transfer Across Domains and Tasks. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; p. 2015. [Google Scholar]
- Long, M.; Wang, J.; Jordan, M.I. Deep Transfer Learning with Joint Adaptation Networks. In Proceedings of the 34th International Conference on Machine Learning; Sydney, Australia, 6–11 August 2017.
- Huang, Z.; Pan, Z.; Lei, B. Transfer Learning with Deep Convolutional Neural Network for SAR Target Classification with Limited Labeled Data. Remote. Sens. 2017, 9, 907. [Google Scholar] [CrossRef] [Green Version]
- Damodaran, B.B.; Courty, N.; Lefevre, S. Sparse Hilbert Schmidt Independence Criterion and Surrogate-Kernel-Based Feature Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 2385–2398. [Google Scholar] [CrossRef] [Green Version]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold Regularization: A Geometric Framework for Learning from Labeled and Unlabeled Examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Wang, B.; Hu, Y.; Gao, J.; Sun, Y.; Chen, H.; Yin, B. Locality Preserving Projections for Grassmann manifold. In Proceedings of the Eighteenth Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lu, J.; Plataniotis, K.; Venetsanopoulos, A. Regularization studies of linear discriminant analysis in small sample size scenarios with application to face recognition. Pattern Recognit. Lett. 2005, 26, 181–191. [Google Scholar] [CrossRef]
- Li, H.; Jiang, T.; Zhang, K. Efficient and Robust Feature Extraction by Maximum Margin Criterion. IEEE Trans. Neural Networks 2006, 17, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.; Xu, N.; Zhang, B.-Y.; Zhang, H.-J.; Yang, Q.; Lin, S. Graph Embedding and Extensions: A General Framework for Dimensionality Reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 29, 40–51. [Google Scholar] [CrossRef] [Green Version]
- Song, L.; Smola, A.; Gretton, A.; Bedo, J.; Borgwardt, K. Feature Selection via Dependence Maximization. J. Mach. Learn. Res. 2012, 13, 1393–1434. [Google Scholar]
- Sugiyama, M.; Idé, T.; Nakajima, S.; Sese, J. Semi-Supervised Local Fisher Discriminant Analysis for Dimensionality Reduction. Mach. Learn. 2010, 78, 35. [Google Scholar] [CrossRef] [Green Version]














| Method | A->B (OA) | A->B (Kappa) | B->A (OA) | B->A (Kappa) | A->C (OA) | A->C (Kappa) |
| DAC | 0.753 | 0.656 | 0.679 | 0.525 | 0.597 | 0.440 |
| TCA | 0.799 | 0.723 | 0.829 | 0.761 | 0.645 | 0.517 |
| SSTCA | 0.809 | 0.737 | 0.839 | 0.774 | 0.667 | 0.546 |
| MIDA | 0.788 | 0.705 | 0.786 | 0.695 | 0.633 | 0.504 |
| SMIDA | 0.788 | 0.705 | 0.798 | 0.717 | 0.655 | 0.539 |
| SMbDA | 0.817 | 0.749 | 0.845 | 0.785 | 0.699 | 0.592 |
| WSMbDA | 0.870 | 0.821 | 0.896 | 0.854 | 0.843 | 0.786 |
| Method | C->A (OA) | C->A (Kappa) | B->C (OA) | B->C (Kappa) | C->B (OA) | C->B (Kappa) |
| DAC | 0.701 | 0.571 | 0.666 | 0.527 | 0.734 | 0.637 |
| TCA | 0.680 | 0.565 | 0.737 | 0.640 | 0.735 | 0.638 |
| SSTCA | 0.684 | 0.570 | 0.773 | 0.686 | 0.735 | 0.638 |
| MIDA | 0.702 | 0.569 | 0.715 | 0.610 | 0.766 | 0.677 |
| SMIDA | 0.720 | 0.610 | 0.715 | 0.610 | 0.766 | 0.677 |
| SMbDA | 0.712 | 0.594 | 0.764 | 0.675 | 0.742 | 0.649 |
| WSMbDA | 0.758 | 0.666 | 0.857 | 0.804 | 0.765 | 0.675 |
| Method | A->B (OA) | A->B (Kappa) | A->C (OA) | A->C (Kappa) | A->D (OA) | A->D (Kappa) |
|---|---|---|---|---|---|---|
| DAC | 0.117 | -0.012 | 0.126 | -0.009 | 0.204 | 0.010 |
| TCA | 0.486 | 0.321 | 0.590 | 0.462 | 0.713 | 0.608 |
| SSTCA | 0.492 | 0.327 | 0.607 | 0.468 | 0.713 | 0.608 |
| MIDA | 0.508 | 0.348 | 0.567 | 0.432 | 0.776 | 0.686 |
| SMIDA | 0.508 | 0.348 | 0.600 | 0.477 | 0.776 | 0.686 |
| SMbDA | 0.529 | 0.369 | 0.636 | 0.524 | 0.758 | 0.666 |
| WSMbDA | 0.667 | 0.549 | 0.841 | 0.775 | 0.808 | 0.733 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Li, P.; Du, B.; Yang, J.; Tian, L.; Li, M.; Zhao, L. Scatter Matrix Based Domain Adaptation for Bi-Temporal Polarimetric SAR Images. Remote Sens. 2020, 12, 658. https://doi.org/10.3390/rs12040658
Sun W, Li P, Du B, Yang J, Tian L, Li M, Zhao L. Scatter Matrix Based Domain Adaptation for Bi-Temporal Polarimetric SAR Images. Remote Sensing. 2020; 12(4):658. https://doi.org/10.3390/rs12040658
Chicago/Turabian StyleSun, Weidong, Pingxiang Li, Bo Du, Jie Yang, Linlin Tian, Minyi Li, and Lingli Zhao. 2020. "Scatter Matrix Based Domain Adaptation for Bi-Temporal Polarimetric SAR Images" Remote Sensing 12, no. 4: 658. https://doi.org/10.3390/rs12040658
APA StyleSun, W., Li, P., Du, B., Yang, J., Tian, L., Li, M., & Zhao, L. (2020). Scatter Matrix Based Domain Adaptation for Bi-Temporal Polarimetric SAR Images. Remote Sensing, 12(4), 658. https://doi.org/10.3390/rs12040658