1. Introduction
Artificial near-Earth satellites are nowadays an effective instrument for Earth observations and the monitoring of global change phenomena. Altimetry satellites provide a continuous data record of global and regional sea level change, see, for example, Reference [
1]. Data from these satellites also allow the investigation of ocean dynamics (large- and small-scale circulation, ocean tides, waves, El Ni
o-Southern Oscillation, coastal processes, etc.), the cryosphere, dynamics of land surface waters, and seafloor topography [
2]. For these applications, a highly accurate (at the 1 cm level) and stable (below 1 mm/year) satellite orbit is required [
3,
4]. The accuracy and stability of altimetry satellite orbits significantly improved in recent decades due to enhancements in, amongst others, modeling the Earth’s time-variable gravity field [
5], reference frame determination [
6,
7], and improvements in modeling non-gravitational perturbations [
8,
9].
Altimetry satellites such as Jason-1/-2/-3 have a non-spherical, complex shape comprising the main satellite body on which solar panels and numerous measurement and positioning instruments are mounted. A detailed overview of the Jason satellite missions goals, spacecraft and payloads is given in Reference [
10] and, for example, the websites of the Earth Observation portal (
https://directory.eoportal.org/web/eoportal/satellite-missions/j/jason-2, Last access: 14 November 2019 and
https://directory.eoportal.org/web/eoportal/satellite-missions/j/jason-3, Last access: 14 November 2019) and the International DORIS Service (IDS;
ftp://ftp.ids-doris.org/pub/ids/satellites/MassCoGInitialValues.txt, Last access: 14 November 2019). Precise information on the size, the optical properties and the orientation in space of the satellite surfaces is important since non-gravitational forces caused by, for example, solar radiation pressure, Earth’s reflected and infrared radiation and atmospheric drag depend on the satellite effective cross-sectional area. In addition, the phase center locations of positioning devices such as a laser ranging array (LRA), a Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) receiver and a Global Navigation Satellite Systems (GNSS) receiver required in the inertial reference frame depend on the satellite orientation in space. Therefore, so called nominal yaw steering models (see also
Section 2.1.1) are defined and can be used to realize a nominal (not ideal) orientation of a spacecraft. In addition to these models, for satellites equipped with star tracking cameras like the Jason satellites, the measured spacecraft orientation is available (see
Section 2.1.2). Until recently, mainly a given functional model (nominal law) has been used for the attitude modeling of the Jason satellites. Thus, five out of six Analysis Centers (ACs) of the International DORIS Service (IDS) used the nominal law to compute the satellite attitude when they computed their contribution to the International Terrestrial Reference Frame realization ITRF2014 (
https://ids-doris.org/analysis-coordination/combination/contributions-to-itrf/contribution-itrf2014.html, Last access: 16 January 2020). Solely the IDS AC at NASA/GSFC (National Aeronautics and Space Administration/Goddard Space Flight Center) [
11] used attitude observations given as satellite body quaternions and solar panel rotation angles for their contribution. Moreover, also the Jason orbits of the Helmholtz-Zentrum Potsdam – Deutsches GeoForschungsZentrum (GFZ, Germany) and the Centre National d’Études Spatiales (CNES, France), which are used for the orbit comparison in
Section 3.3, were derived using an observation-based attitude. Another example of the use of observation-based attitude information can be found for the CryoSat-2 satellite [
12].
In this paper, we investigate the impact of the observation-based (measured) spacecraft attitude realization in comparison to the modeled nominal yaw steering attitude for the three altimetry satellites Jason-1/-2/-3 [
13]. We compare the root mean square (RMS) fits of Satellite Laser Ranging (SLR) observations and quantify the impact on estimated parameters such as scaling factors for the solar radiation pressure, Earth’s albedo and thermospheric drag. Empirical accelerations in the along-track and cross-track directions are studied as well as station coordinate time series. Additionally, the derived orbits are compared with selected external orbits and, finally, the RMS and the mean of single-satellite altimetry crossover differences and radial errors are evaluated. This analysis allows the investigation of the impact of the satellite attitude modeling on geographically correlated mean errors (GCEs). In this paper, we use the word “mean” to abbreviate the “arithmetic mean”.
The paper is organized as follows. The first part of
Section 2 provides information on two satellite attitude modeling strategies, namely, the nominal yaw steering model and the observation-based attitude realization. The second part of
Section 2 describes the models used for orbit determination for these satellites. The POD and altimetry results of these tests are described in
Section 3. Finally,
Section 4 discusses the obtained results and concludes the paper.
4. Discussion and Conclusions
In this paper, the differences in the attitude realization (observation-based compared to nominal yaw steering) in the POD of the Jason satellites are investigated. The impact of the different attitude realization strategies on satellite orbits is evaluated and consequences for derived geodetic parameters such as station repeatability and sea level estimates are quantified and discussed. The observation-based satellite attitude information comprise quaternions of the spacecraft body and rotation angles of the solar arrays. Nominally, the attitude can also be realized using a yaw steering model depending on the angle. At DGFI-TUM, a preprocessing algorithm for the observation-based attitude data was developed. This algorithm comprises the elimination of outliers, a temporal resampling of the data and the optimal interpolation of missing data. Using SLR observations to all three Jason satellites over a time interval of approximately 25 years, precise orbits are computed using both attitude approaches.
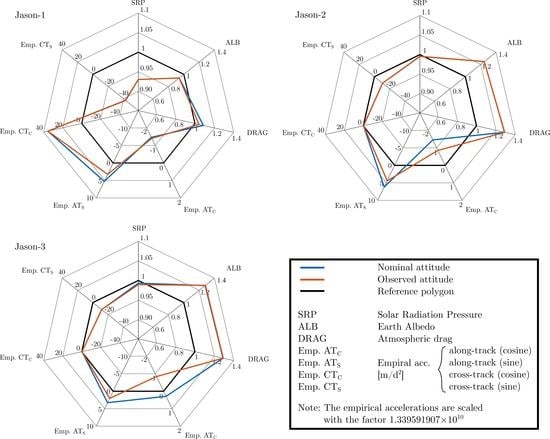
The analysis of the computed satellite orbits shows that using preprocessed observation-based attitude data reduces the averages of the arc-wise RMS fits of SLR observations by 5.93% (Jason-1), 8.27% (Jason-2) and 4.51% (Jason-3). The estimated orbital parameters such as solar radiation pressure scaling factors, Earth’s albedo scaling factors, scaling factors for the thermospheric drag and coefficients of empirical accelerations obtained within a POD are analysed. Using observation-based attitude data significantly reduces the amplitudes of the parameter variations especially at draconitic periods.
The comparison of the DGFI-TUM orbits with external solutions of GFZ and CNES shows about 10% reduction of the standard deviations of the component-wise (along-track, cross-track, radial) orbit differences when using observation-based DGFI-TUM orbits. All orbit differences are of the same order of magnitude despite the fact that the GFZ and CNES orbits are based on a combination of geodetic space techniques, namely SLR and DORIS for GFZ and DORIS and GPS for CNES.
Furthermore, the impact of both orbit solutions on the estimated SLR station coordinates is investigated. Orbit specific periods (draconitic period and its harmonics) are reduced in the station coordinate time series using the observation-based satellite orbits. This allows a more reliable interpretation of geophysical signals in the station coordinate time series since modeling errors of the orbit do not cause them to deteriorate.
Our results prove that using observed attitude information is clearly better than utilizing models describing an intentional orientation. While the nominal model, in general, defines the long-wavelength behavior of the satellite orbit, observation-based data benefit the consideration of short-wave signals in the satellite orbit. The use of the actual attitude information allows a much more accurate determination of the perturbing forces. Hence, the computed satellite position is closer to the actual position and the differences between the observed and computed SLR observations are smaller. It has to be mentioned that the quaternions and solar panel orientation angles are considered to be error-free, that is, no standard deviations are considered.
The benefits for, for example, altimetry products are twofold. First, an improved satellite attitude corrects the position of the onboard altimeter in the GCRS. This implies an improvement of the measured sea surface height. Additionally, the pointing and consequently the georeferencing of the altimeter measurement footprint is more precise. Our single-satellite altimetry crossover analysis shows that the mean of absolute crossover differences is reduced by 6% for Jason-1, 15% for Jason-2, and 16% for Jason-3 when observation-based orbits are used. Also radial and geographically correlated mean errors are reduced. The potentially enhanced altimetry measurements can be used for computation of such products as sea surface topography, significant wave heights, ocean tides as well as global and regional sea level products. Using corrected measurements should increase the reliability of the mean observed global and local sea level change.
In this paper, only SLR observations are used for the computation of satellite orbits. In future investigations, a combination of geodetic tracking techniques for POD should be evaluated. DORIS and GNSS provide a considerably large and continuous number of satellite observations. Thus, the benefit of using attitude observation data in combination with these tracking techniques should be compared to the SLR-only results. To quantify the enhancement of the observation-based attitude approach at different orbit geometries, the investigation should be extended for other satellite missions. Therefore, the preprocessed observation data and the experience in data processing might be useful for other institutes.
The improved orbits might also benefit other scientific disciplines, too. The corrected time series of station coordinates can be used to improve geophysical models. Moreover, beneficial or adverse effects on the Terrestrial Reference Frame can be further discussed. Based on the findings of the prior described investigation, it can be clearly stated that attitude observations help to further improve the POD of near-Earth satellites. Moreover, in this study, it was shown that an improved satellite attitude handling not only exceeds an improvement of the POD but further beneficially affects derived geodetic or geophysical parameters.
The preprocessed observation-based attitude data of Jason-1/-2/-3 will be made available on request at DGFI-TUM (contact responsible author of this manuscript).